E. M. Elabbasy 1, M. Y. Barsom 1, F. S. AL-dheleai 2
1Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt
2Department of Mathematics, Faculty of Education and Languages, Amran University, Amran, Yamen
Correspondence to: E. M. Elabbasy , Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, via comparison with first order oscillatory difference equations and by a Riccati transformation technique, we will study the oscillatory behavior of third order nonlinear neutral difference equations. We establish some new sufficient conditions which insure that every solution of this equation either oscillates or converges to zero. Our results improve and extend some known results in the literature. Examples are given to illustrate the importance of the results.
Keywords:
Oscillatory Solutions, Third Order, Nonlinear, Neutral, Difference Equation
Cite this paper: E. M. Elabbasy , M. Y. Barsom , F. S. AL-dheleai , Oscillation Results for Third Order Nonlinear Neutral Delay Difference Equations, Applied Mathematics, Vol. 3 No. 5, 2013, pp. 171-184. doi: 10.5923/j.am.20130305.04.
1. Intrduction
By comparison with some first difference equations whose oscillatory characters are known and by means of a Riccati transformation technique, we obtain several new sufficient conditions for the oscillation of all solutions of the nonlinear neutral difference equation of the form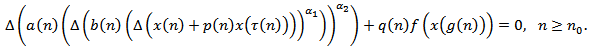 | (1.1) |
Where 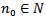 is a fixed integer,
is a fixed integer,  denotes the forward difference operator defined by
denotes the forward difference operator defined by 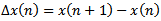 and
and 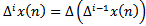 . Throughout this paper, we will assume the following hypotheses: (A1)
. Throughout this paper, we will assume the following hypotheses: (A1) 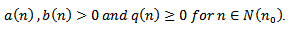 (A2)
(A2) 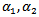 are quotient of odd positive integers.(A3)
are quotient of odd positive integers.(A3) 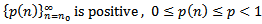 .(A4)
.(A4) 
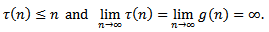 (A5)
(A5) 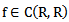 such that
such that 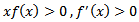
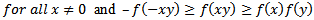
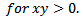 In addition, we will make use of the following conditions:
In addition, we will make use of the following conditions: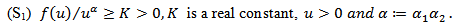
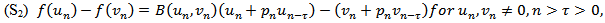
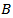 is a nonnegative real valued function,
is a nonnegative real valued function, 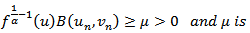 a constant.We set
a constant.We set 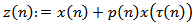 . By a solution of equation (1.1) we mean a nontrivial sequence
. By a solution of equation (1.1) we mean a nontrivial sequence 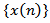 defined on
defined on 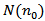 , which satisfies equation (1.1) for all
, which satisfies equation (1.1) for all 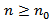 . A solution
. A solution 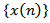 of equation (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise. Equation (1.1) is called oscillatory if all its solutions are oscillatory. In recent years, there has been an increasing interest in the study of the problem of determining the oscillation and non-oscillation of solutionsof difference equations of the form (1.1) and its special cases. In[1], Graef et al. proved several theorems provided sufficient conditions foroscillation of all solutions of the third order difference equation of the form
of equation (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise. Equation (1.1) is called oscillatory if all its solutions are oscillatory. In recent years, there has been an increasing interest in the study of the problem of determining the oscillation and non-oscillation of solutionsof difference equations of the form (1.1) and its special cases. In[1], Graef et al. proved several theorems provided sufficient conditions foroscillation of all solutions of the third order difference equation of the form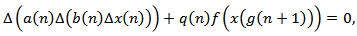 | (1.2) |
depend on condition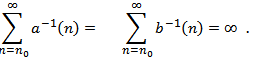 | (1.3) |
In[2], via comparison with first order oscillatory difference equations, Agarwal et al. proved several theorems provided sufficient conditions for oscillation of all solutions of the third order difference equation of the form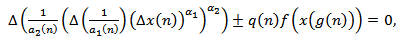 | (1.4) |
depend on condition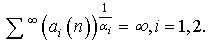 | (1.5) |
In[3], by a Riccati transformation technique, Schmeidel studied the oscillatory and asymptotic behavior of solutions of the third order difference equation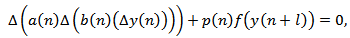 | (1.6) |
using the condition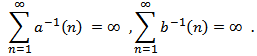 | (1.7) |
In[4], via comparison with first order oscillatory difference equations, Grace et al. discussed the oscillatory behavior of the solutions of the difference equation of the form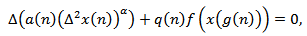 | (1.8) |
under the condition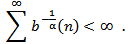 | (1.9) |
In[5], by a Riccatitransformation technique, Selvaraj et al. established some sufficient conditionsforoscillation of all solutions of the third order non-linear difference equation of the form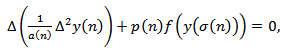 | (1.10) |
using the condition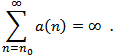 | (1.11) |
In[6], Saker et al. studied the oscillatory behavior of solutions of the equation 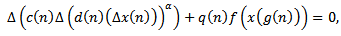 | (1.12) |
using the condition (1.7) and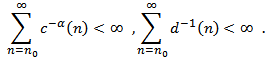 | (1.13) |
In[7], Thandapani et al. considered the third order difference equation of the form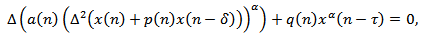 | (1.14) |
under the condition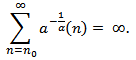 | (1.15) |
In[8], using condition (1.11) Selvaraj et al. considered nonlinear third-order difference equations of the form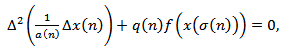 | (1.16) |
and they study the oscillatory behavior of solutions of equation (1.16). In[9], Saker investigated the third-order difference equation (1.12) using the condition (1.13) and the authorobtained some Hille and Nehari type criteria for the oscillation of equation (1.12). For further results concerning the oscillatory and asymptotic behavior of thirdorder difference equation we refer to the books[10, 11, 12] and the references cited therein. Our results improve and extend some known results in the literature. The paper is organized as follows. In Section 2, we will state and prove the main oscillation theorems, in Section 3, and Section 4, we will give some remarks and provide some examples to illustrate the main results.
2. Main Results
In this section, we establish some new oscillation criteria for the equation (1.1) under the following conditions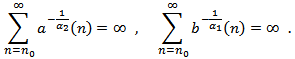 | (2.1) |
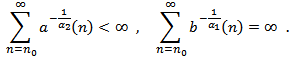 | (2.2) |
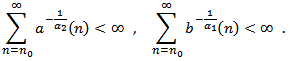 | (2.3) |
In the following results, we shall use the following notations: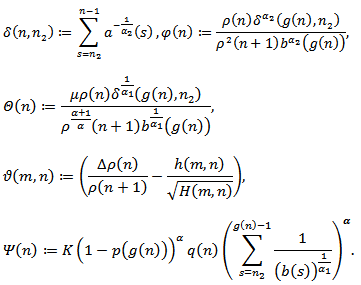 We assume that there exists a double sequence
We assume that there exists a double sequence 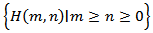 and
and 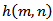 such that
such that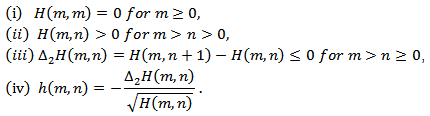 We begin with some useful lemmas, which will be used in obtaining our main results. The proof of the following Lemmas are similar to that of (Lemma 2.1, 2.2 and 2.3 respectively in[13]) and hence the details are omitted.Lemma 2.1. Let
We begin with some useful lemmas, which will be used in obtaining our main results. The proof of the following Lemmas are similar to that of (Lemma 2.1, 2.2 and 2.3 respectively in[13]) and hence the details are omitted.Lemma 2.1. Let 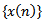 be an eventually positive solution of the equation (1.1) and suppose that
be an eventually positive solution of the equation (1.1) and suppose that 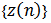 satisfies
satisfies 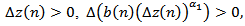
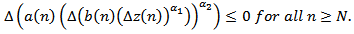 Then there exists
Then there exists 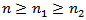 such that
such that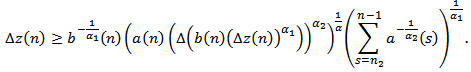 | (2.4) |
Lemma 2.2. Assume that (2.1) holds. Let 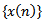 be an eventually positive solution of equation (1.1). Then for sufficiently large
be an eventually positive solution of equation (1.1). Then for sufficiently large 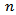 , there are only two possible cases:
, there are only two possible cases: 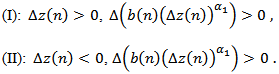 Lemma 2.3. Assume that (2.1) holds. Let
Lemma 2.3. Assume that (2.1) holds. Let 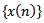 be an eventually positive solution of the equation (1.1) and suppose that Case (II) of Lemma 2.2 holds. If
be an eventually positive solution of the equation (1.1) and suppose that Case (II) of Lemma 2.2 holds. If 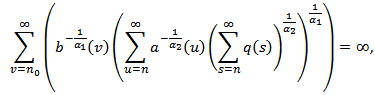 | (2.5) |
then 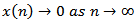 .Theorem 2.1. Let (2.1) and (2.5) hold. If the first order delay equation
.Theorem 2.1. Let (2.1) and (2.5) hold. If the first order delay equation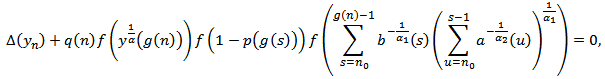 | (2.6) |
is oscillatory then equation (1.1) is oscillatory or 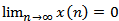 .Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
.Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 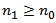 such that
such that 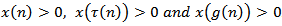 . From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. From Lemma (2.1), we have
. From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. From Lemma (2.1), we have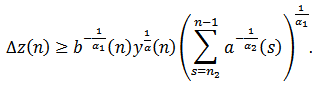 where
where 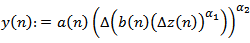 . Summing the above inequality from
. Summing the above inequality from 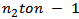 , we obtain
, we obtain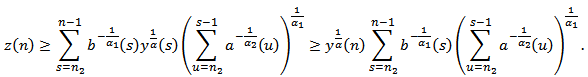 | (2.7) |
There exists a 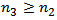 with
with 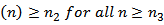 , such that
, such that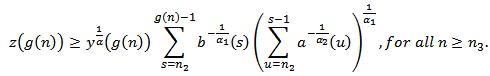 | (2.8) |
Since 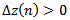 and
and 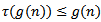 , then
, then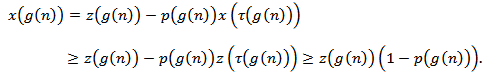 | (2.9) |
From (2.8), we obtain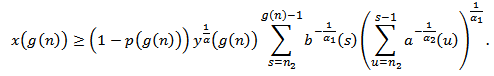 From equation (1.1),
From equation (1.1), 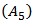 and the last inequality , we obtain,
and the last inequality , we obtain, 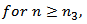
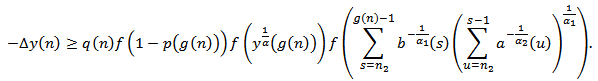 Summing the last inequality from
Summing the last inequality from 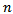 to
to 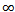 , we get
, we get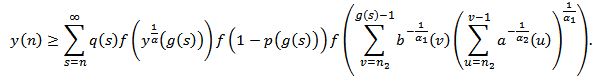 The sequence
The sequence 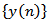 is obviously strictly decreasing. Hence, by the discrete analog of Theorem 1 in[14] we conclude that there exists a positive solution
is obviously strictly decreasing. Hence, by the discrete analog of Theorem 1 in[14] we conclude that there exists a positive solution 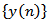 of equation (2.6) which tends to zero. This contradicts that (2.6) is oscillatory. If the (II) holds, we are then back to the proof of Lemma 2.3 to show that
of equation (2.6) which tends to zero. This contradicts that (2.6) is oscillatory. If the (II) holds, we are then back to the proof of Lemma 2.3 to show that 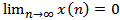 . The proof is complete.Theorem 2.2. Assume that (2.2), (2.5) and (2.6) hold. If
. The proof is complete.Theorem 2.2. Assume that (2.2), (2.5) and (2.6) hold. If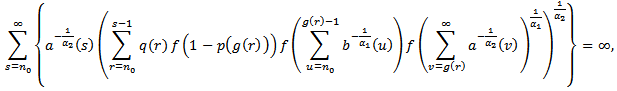 | (2.10) |
then every solution of equation (1.1) oscillatory or 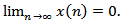 Proof. Let
Proof. Let 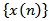 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 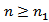 . Say
. Say 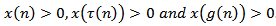 . Based on condition (2.2), there exist three possible cases (I), (II) (as those of Lemma 2.2), and
. Based on condition (2.2), there exist three possible cases (I), (II) (as those of Lemma 2.2), and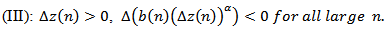 Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 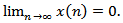 . Assume that (III) holds. Then, we have
. Assume that (III) holds. Then, we have 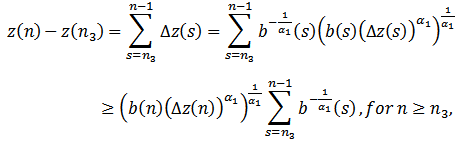 There exists a
There exists a 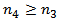 with
with 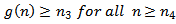 , such that
, such that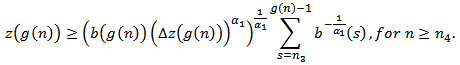 From equation (1.1), (2.9),
From equation (1.1), (2.9), 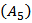 and the last inequality, we obtain,
and the last inequality, we obtain, 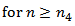
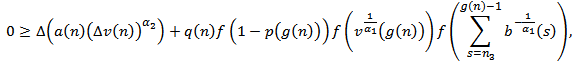 | (2.11) |
where 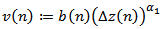 . It is clear that
. It is clear that 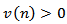 and
and 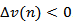 . It follows that
. It follows that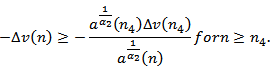 Summing the last inequality from n to
Summing the last inequality from n to 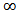 , we obtain
, we obtain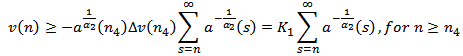 where
where 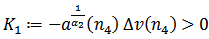 . There exists a
. There exists a 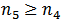 with
with 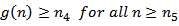 , such that
, such that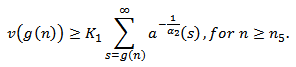 Summing (2.11) from
Summing (2.11) from 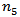 to
to 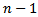 and using the above inequality, we find
and using the above inequality, we find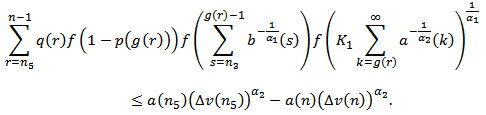 In view of
In view of 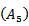 , we see that
, we see that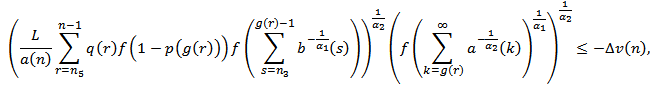 where
where 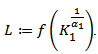 Summing the above inequality from
Summing the above inequality from 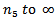 , we obtain
, we obtain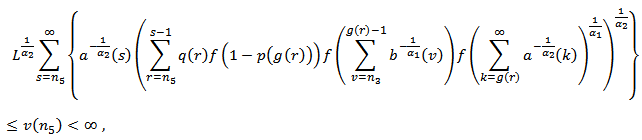 which contradicts the condition (2.10). The proof is complete.Theorem 2.3. Assume that (2.3), (2.5), (2.6) and (2.10) hold. If
which contradicts the condition (2.10). The proof is complete.Theorem 2.3. Assume that (2.3), (2.5), (2.6) and (2.10) hold. If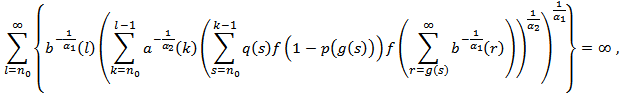 | (2.12) |
then every solution of equation (1.1) oscillatory or 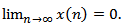 Proof. Let
Proof. Let 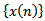 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 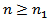 . Say
. Say 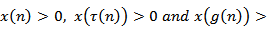
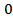 . By (2.3), there exist four possible cases: (I), (II), (III) (as those of Theorem 2.2) and
. By (2.3), there exist four possible cases: (I), (II), (III) (as those of Theorem 2.2) and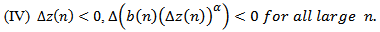 Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 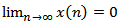 . Assume that (III) holds. Then we are back to the proof of Theorem 2.2 to get contradiction to (2.10). Assume that (IV) holds. We one can choose
. Assume that (III) holds. Then we are back to the proof of Theorem 2.2 to get contradiction to (2.10). Assume that (IV) holds. We one can choose 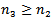 with
with 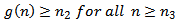 , such that
, such that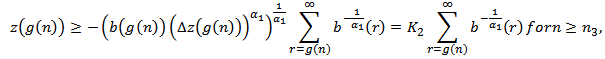 where
where 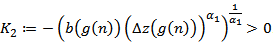 . Thus equation (1.1), (2.9) and
. Thus equation (1.1), (2.9) and 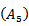 yield
yield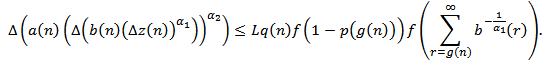 where
where 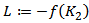 . Summing the above inequality from
. Summing the above inequality from 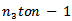 , we find
, we find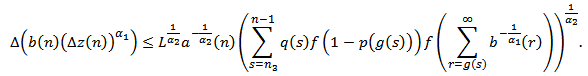 Again summing the above inequality from
Again summing the above inequality from 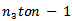 , we find
, we find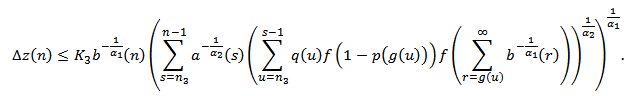 where
where 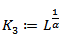 . Finally, summing the above inequality from
. Finally, summing the above inequality from 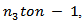 we have
we have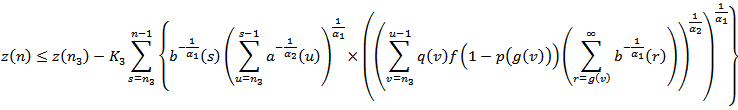 .From condition (2.12), we get
.From condition (2.12), we get 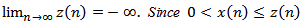 then,
then, 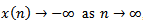 , which contradicts the fact that
, which contradicts the fact that 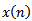 is a positive solution of (1.1). The proof is complete.Theorem 2.4. Let
is a positive solution of (1.1). The proof is complete.Theorem 2.4. Let 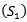 , (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence
, (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence 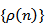 , such that
, such that 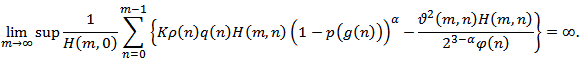 | (2.13) |
Then every solution of equation (1.1) oscillatory or 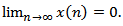 Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 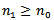 such that
such that 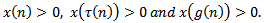 From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence
From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence 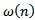 by
by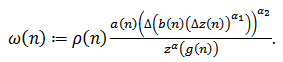 | (2.14) |
Then 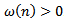 . From (2.14), we have
. From (2.14), we have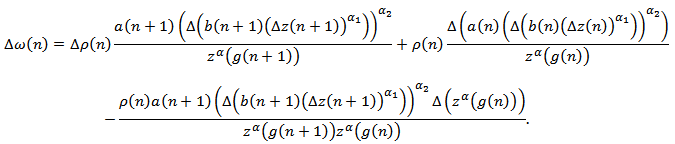 Now, by using the inequality
Now, by using the inequality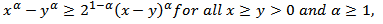 | (2.15) |
then, we have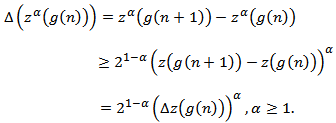 Thus
Thus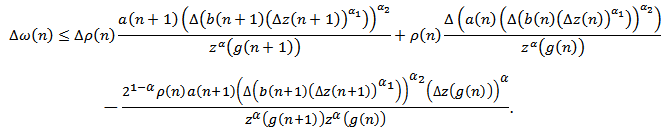 | (2.16) |
From 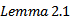 , there exists
, there exists 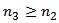 with
with 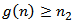 for all
for all 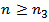 such that
such that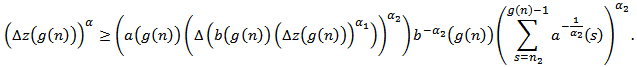 | (2.17) |
Since 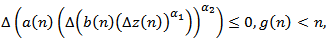 we get
we get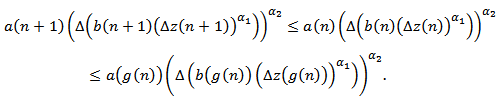 | (2.18) |
From (2.16), (2.17) and (2.18), we obtain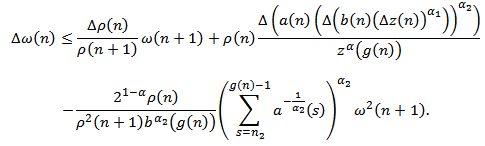 From (2.9), we obtain
From (2.9), we obtain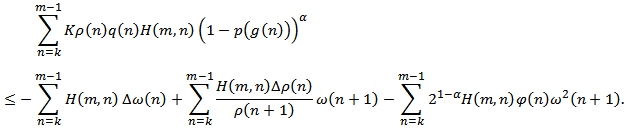 Which yields after summing by parts
Which yields after summing by parts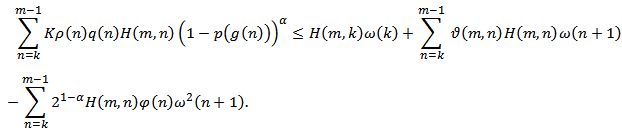 Using the inequality
Using the inequality 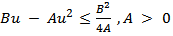 , we have
, we have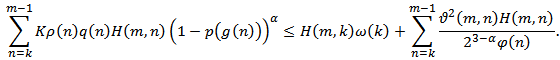 | (2.19) |
Then,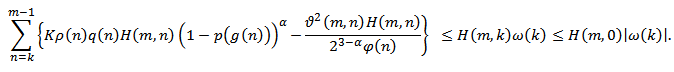 Hence,
Hence,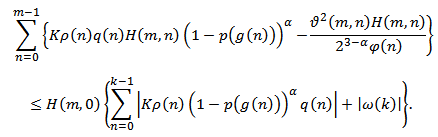 Hence,
Hence,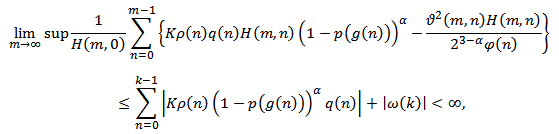 which is contrary to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
which is contrary to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 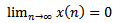 . This completes the proof of Theorem 2.4.Corollary 2.1. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by
. This completes the proof of Theorem 2.4.Corollary 2.1. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by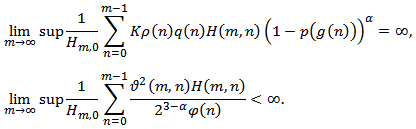 Then equation(1.1) is oscillatory or
Then equation(1.1) is oscillatory or 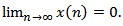 When
When 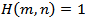 , we obtain the following resultCorollary 2.2. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by
, we obtain the following resultCorollary 2.2. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by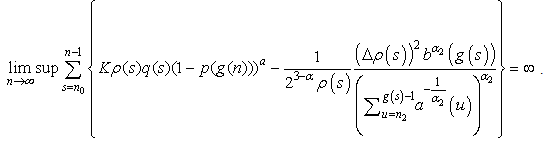 | (2.20) |
Then equation (1.1) is oscillatory or 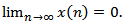 Theorem 2.5. Assume that
Theorem 2.5. Assume that 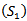 , (2.2), (2.5), and (2.13) hold. If
, (2.2), (2.5), and (2.13) hold. If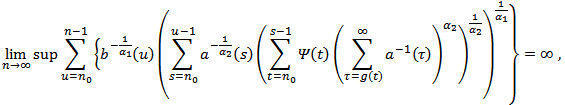 | (2.21) |
then every solution of equation (1.1) oscillatory or 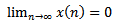 .Proof. Let
.Proof. Let 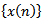 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 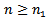 . Say
. Say 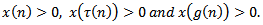 Based on condition (2.2), there exist three possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Based on condition (2.2), there exist three possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 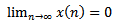 . Assume that (III) holds. Then, there exists
. Assume that (III) holds. Then, there exists 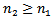 such that
such that 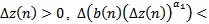
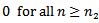 . Then, we have
. Then, we have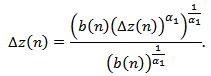 Summing the above inequality from
Summing the above inequality from 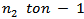 , we obtain
, we obtain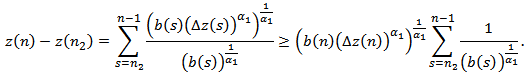 | (2.22) |
Hence there exists a 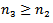 such that
such that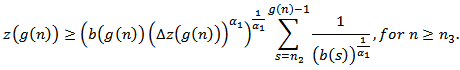 From equation (1.1),
From equation (1.1), 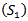 , (2.9) and the last inequality, we obtain
, (2.9) and the last inequality, we obtain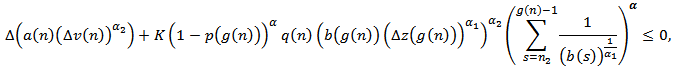 | (2.23) |
where 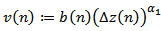 . It is clear that
. It is clear that 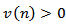 and
and 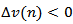 . It follows that
. It follows that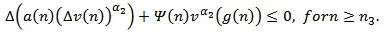 | (2.24) |
Since 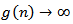 as
as 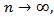 we can choose
we can choose 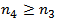 such that
such that 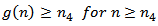 and thus
and thus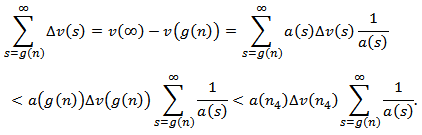 Thus
Thus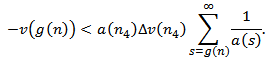 Substituting back in (2.24), we have
Substituting back in (2.24), we have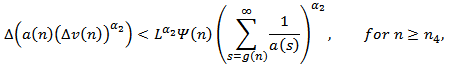 | (2.25) |
where 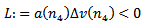 . Summing this inequality from
. Summing this inequality from 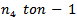 , we see that
, we see that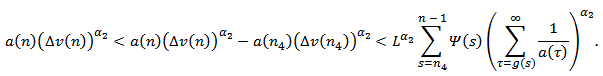 where
where 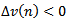 . Summing again from
. Summing again from 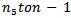 , we have
, we have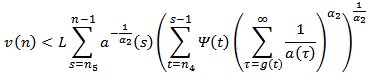 or equivalently
or equivalently 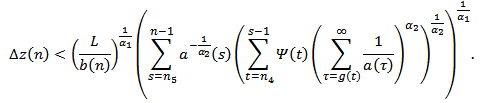 Summing from
Summing from 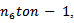 we have
we have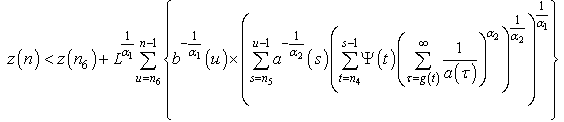 By condition (2.21), we have
By condition (2.21), we have 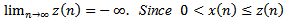 then,
then, 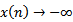 as
as 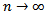 which contradicts the fact that
which contradicts the fact that 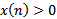 . The proof is complete.Theorem 2.6. Assume that
. The proof is complete.Theorem 2.6. Assume that 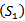 , (2.3), (2.5), (2.13), and (2.21) hold. If
, (2.3), (2.5), (2.13), and (2.21) hold. If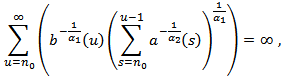 | (2.26) |
then every solution of equation (1.1) oscillatory or 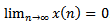 .Proof. Let
.Proof. Let 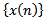 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 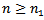 . Based on condition (2.3), there exist four possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.4 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
. Based on condition (2.3), there exist four possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.4 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 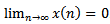 . Assume that (III) holds. Then we are back to the proof of Theorem 2.5 to get contradiction to (2.21). Assume that (IV) holds. Since
. Assume that (III) holds. Then we are back to the proof of Theorem 2.5 to get contradiction to (2.21). Assume that (IV) holds. Since 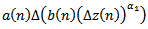 is non-increasing sequence there exists a negative constant
is non-increasing sequence there exists a negative constant 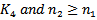 such that
such that 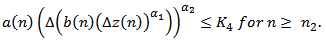 Dividing by
Dividing by 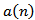 and summing the last inequality from
and summing the last inequality from 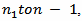 we obtain
we obtain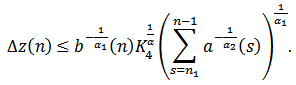 Summing the last inequality from
Summing the last inequality from 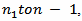 we obtain
we obtain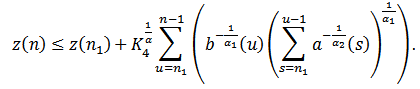 From condition (2.26), we get
From condition (2.26), we get 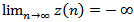 . Since
. Since 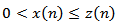 then,
then, 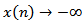 as
as 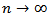 , which contradicts the fact that
, which contradicts the fact that 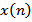 is a positive solution of (1.1). The proof is complete.Theorem 2.7. Let
is a positive solution of (1.1). The proof is complete.Theorem 2.7. Let 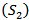 , (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence
, (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence 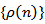 , such that
, such that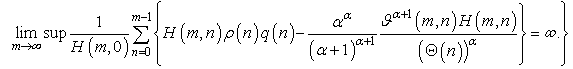 | (2.27) |
Then every solution of equation (1.1) oscillatory or 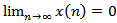 .Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
.Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 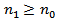 such that
such that 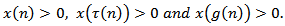 From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence
From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence 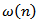 by
by 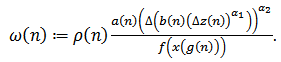 | (2.28) |
Then 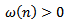 . From (2.28) and
. From (2.28) and 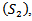 we have
we have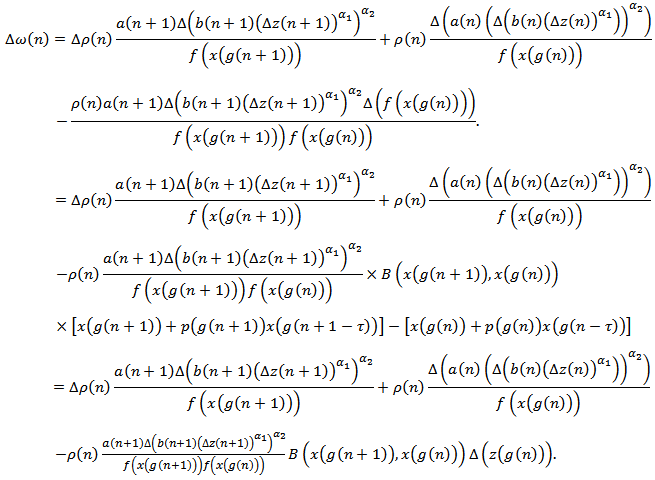 | (2.29) |
From Lemma 2.1, there exists 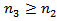 with
with 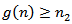 for all
for all 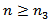 such that
such that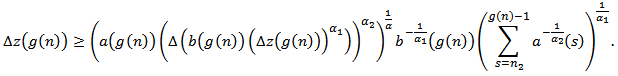 | (2.30) |
From (2.18) and (2.29), we have 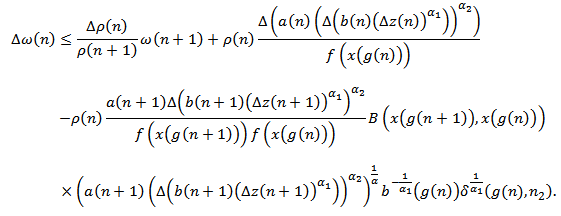 | (2.31) |
From (1.1), (2.28),  and (2.31), we have
and (2.31), we have 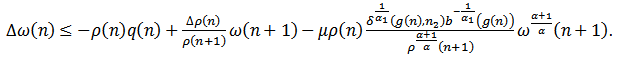 | (2.32) |
Therefore, we have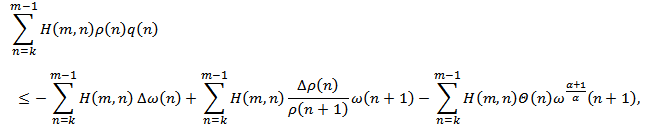 which yields after summing by parts
which yields after summing by parts 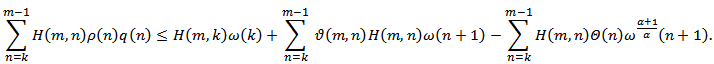 Using the inequality
Using the inequality 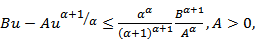 we have
we have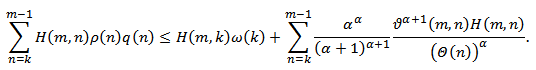 Then,
Then,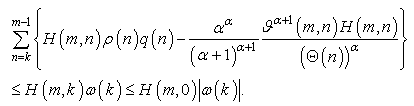 Hence,
Hence,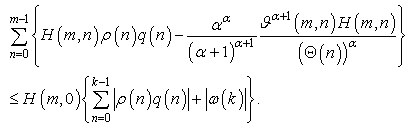 Hence,
Hence,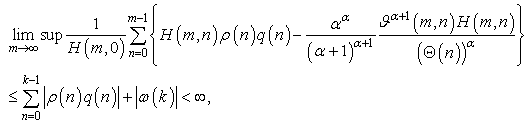 which is contrary to (2.27). Assume that (II)holds. Then we are back to the proof of Lemma 2.3 to show that
which is contrary to (2.27). Assume that (II)holds. Then we are back to the proof of Lemma 2.3 to show that 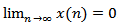 . This completes the proof of Theorem 2.7.From Theorem 2.7, if
. This completes the proof of Theorem 2.7.From Theorem 2.7, if 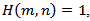 we get the following resultCorollary 2.3. Assume that all the assumptions of Theorem 2.7 hold, except the condition (2.27) is replaced by
we get the following resultCorollary 2.3. Assume that all the assumptions of Theorem 2.7 hold, except the condition (2.27) is replaced by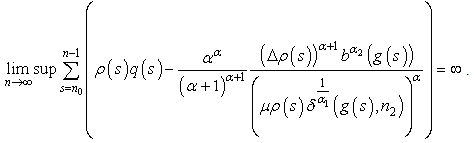 Then equation(1.1) is oscillatory or
Then equation(1.1) is oscillatory or 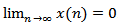 .Theorem 2.8. Assume that (2.2), (2.5), (2.27) and (2.10) hold. Then every solution of equation (1.1) oscillatory or
.Theorem 2.8. Assume that (2.2), (2.5), (2.27) and (2.10) hold. Then every solution of equation (1.1) oscillatory or 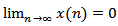 .Proof. The proof is similar to that of Theorem 2.2, Theorem 2.7 and hence the details are omitted.Theorem 2.9. Assume that (2.3), (2.5), (2.27), (2.10) and (2.12) hold. Then every solution of equation (1.1) oscillatory or
.Proof. The proof is similar to that of Theorem 2.2, Theorem 2.7 and hence the details are omitted.Theorem 2.9. Assume that (2.3), (2.5), (2.27), (2.10) and (2.12) hold. Then every solution of equation (1.1) oscillatory or 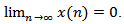 Proof. The proof is similar to that of Theorem 2.3, Theorem 2.7 and hence the details are omitted.
Proof. The proof is similar to that of Theorem 2.3, Theorem 2.7 and hence the details are omitted.
3. Conclusions
In this paper, we established some new sufficient conditions which insure that every solution of this equation either oscillates or converges to zero. Our results improved and expanded some known results, see e.g. the following results :Remark 3.1. If 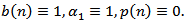 Then Theorem 2.3 reduced to a special case Theorem 2.1 in[4].Remark 3.2. If
Then Theorem 2.3 reduced to a special case Theorem 2.1 in[4].Remark 3.2. If 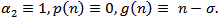 Then Theorem 2.4 extended and improved Theorem 6 in[6].Remark 3.3.
Then Theorem 2.4 extended and improved Theorem 6 in[6].Remark 3.3. 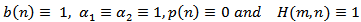 . Then Theorem 2.4 reduced to a special case of Theorem 1 in[5].Remark 3.4. If
. Then Theorem 2.4 reduced to a special case of Theorem 1 in[5].Remark 3.4. If 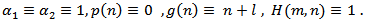 Then Theorem 2.4 extended and improved Theorem 3 in[3].Remark 3.5. If
Then Theorem 2.4 extended and improved Theorem 3 in[3].Remark 3.5. If 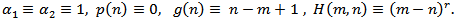 Then Theorem 2.4 reduced to a special case of Theorem 1 in[1].Remark 3.6. If
Then Theorem 2.4 reduced to a special case of Theorem 1 in[1].Remark 3.6. If 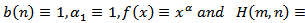 Then Theorem 2.4 extended and improved Theorem 2.7 and Theorem 2.8 in[7].Remark 3.7. If
Then Theorem 2.4 extended and improved Theorem 2.7 and Theorem 2.8 in[7].Remark 3.7. If 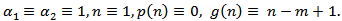 Then Corollary 2.2 reduced to a special case of Theorem 2 in[1].Remark 3.8. If
Then Corollary 2.2 reduced to a special case of Theorem 2 in[1].Remark 3.8. If 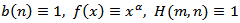 . Then Theorem 2.7 extended and improved Theorem 2.5 and Theorem 2.6 in[7].Remark 3.9. If
. Then Theorem 2.7 extended and improved Theorem 2.5 and Theorem 2.6 in[7].Remark 3.9. If 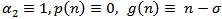 . Then Theorem 2.9 extended and improved Theorem 15 in[6].Remark 3.10. If
. Then Theorem 2.9 extended and improved Theorem 15 in[6].Remark 3.10. If 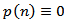 . Then we extended and improved Theorems in[2].Remark 3.11. If
. Then we extended and improved Theorems in[2].Remark 3.11. If 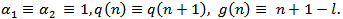 Then we reduced to Theorems in[8].Remark 3.12. If
Then we reduced to Theorems in[8].Remark 3.12. If 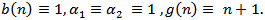 Then we reduced to Theorems in[15].
Then we reduced to Theorems in[15].
4. Examples
In this section we will show the applications of our oscillation criteria by three examples. We will see that the equations in the example is oscillatory or tend to zero based on the results in Section 2.Example 4.1. Consider the difference equation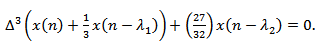 | (4.1) |
If we take 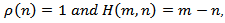 then all conditions of theorem 2.4 are also satisfied. Hence every solution of (4.1) is oscillatory or satisfies
then all conditions of theorem 2.4 are also satisfied. Hence every solution of (4.1) is oscillatory or satisfies 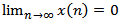 .Example 4.2. Consider the third order nonlinear neutral difference equation
.Example 4.2. Consider the third order nonlinear neutral difference equation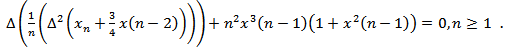 | (4.2) |
If we take 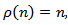 then, Corollary 2.2 asserts that every solution of (4.2) is oscillatory or tend to zero.Example 4.3. Consider the third order difference equationBy choosing
then, Corollary 2.2 asserts that every solution of (4.2) is oscillatory or tend to zero.Example 4.3. Consider the third order difference equationBy choosing 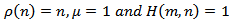 . Then, by Theorem 2.7, we conclude that every solution of (4.3) either oscillates or tend to zero.
. Then, by Theorem 2.7, we conclude that every solution of (4.3) either oscillates or tend to zero.
ACKNOWLEDGMENTS
The authors would like to thank the anonymous referees very much for valuable suggestions, corrections and comments, which results in a great improvement in the original manuscript.
References
| [1] | J. Graef and E. Thandapani, (1999), Oscillatory and asymptotic behavior of solutions of third order delay difference equations, Funk. Ekvac., (42) 355-369. |
| [2] | R. P. Agarwal, S. R. Grace, and D. O’Regan, 2005, On the oscillation of certain third-order difference equations, Adf. Diff. Equ., (3) 345–367. |
| [3] | E. Schmeidel, 2006, Oscillatory and asymptotically zero solutions of third order difference equations with quasi differences, Opus. Math., (26) 361-369. |
| [4] | S .R. Grace, R. P. Agarwal and J. Graef, 2009, Oscillation criteria for certain third order nonlinear difference equations, Appl. Anal. Disc. Math.,(3) 27-38. |
| [5] | B. Selvaraj and I. M. A. Jaffer, 2010, On the oscillation of the solution to third order nonlinear difference equations, J. comp. & Math. Sci., (7) 873-876. |
| [6] | S. H. Saker, J. O. Alzabut and A. Mukheimer, 2010, On the oscillatory behavior for a certain class of third order nonlinear delay difference equations, Elec. J. Qual. Theo. Diff. Eqn., (67) 1-16. |
| [7] | E. Thandapani, M. Vijaya and T Li, 2011, On the oscillation of third order half-linear neutral type difference equations, Elec. J. Qual. Theo. Diff. Eq., (76) 1-13. |
| [8] | B. Selvaraj, P. Mohankumar and A. Balasubramanian, 2012, Oscillatory solutions of certain third order non-linear difference equations, Inter. J. Non-linear Sci., pp (14) 216-219. |
| [9] | S. H. Saker, 2012, Oscillation of certain class third order nonlinear difference equations, Bul. Malays. Math. Sci. Soc., (35) 651-669. |
| [10] | R. P. Agarwal, M. Bohner, S. R. Grace and D. O’Regan, Discret oscillation theory, Hindawi publishing corporation, New York (2005). |
| [11] | I. Gyori, G. Ladas, Oscillation theory of delay differential equations with applications, Clarendon Press, Oxford 1991. |
| [12] | W. G. Kelly and A. C. Peterson, Difference equations, An introduction with applications, Academic Press, New York 1991. |
| [13] | E. M. Elabbasy, M. Y. Barsom and F. S. AL-dheleai, 2013, Oscillation properties of third order nonlinear delay difference Equations, Euro. Inte. J. Sinc. and Tech., (2) 97-116. |
| [14] | Ch. G. Philos, 1981, On the existence of nonoscillatory solutions tending to zero at for differential equations with positive delays. Arch. Math., (36) 168-178. |
| [15] | B. Selvaraj and I. M. A. Jaffer, 2011, Oscillation properties of solutions for certain nonlinear difference equations of third order, Inter. J. Sci. & Eng., (2) 1-9. |

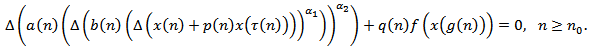
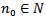 is a fixed integer,
is a fixed integer,  denotes the forward difference operator defined by
denotes the forward difference operator defined by 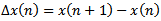 and
and 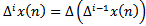 . Throughout this paper, we will assume the following hypotheses: (A1)
. Throughout this paper, we will assume the following hypotheses: (A1) 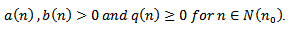 (A2)
(A2) 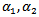 are quotient of odd positive integers.(A3)
are quotient of odd positive integers.(A3) 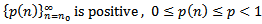 .(A4)
.(A4) 
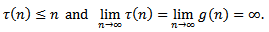 (A5)
(A5) 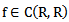 such that
such that 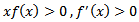
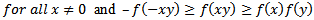
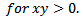 In addition, we will make use of the following conditions:
In addition, we will make use of the following conditions: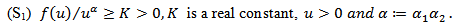
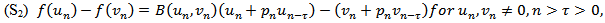
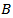 is a nonnegative real valued function,
is a nonnegative real valued function, 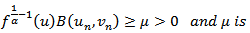 a constant.We set
a constant.We set 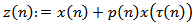 . By a solution of equation (1.1) we mean a nontrivial sequence
. By a solution of equation (1.1) we mean a nontrivial sequence 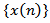 defined on
defined on 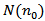 , which satisfies equation (1.1) for all
, which satisfies equation (1.1) for all 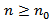 . A solution
. A solution 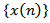 of equation (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise. Equation (1.1) is called oscillatory if all its solutions are oscillatory. In recent years, there has been an increasing interest in the study of the problem of determining the oscillation and non-oscillation of solutionsof difference equations of the form (1.1) and its special cases. In[1], Graef et al. proved several theorems provided sufficient conditions foroscillation of all solutions of the third order difference equation of the form
of equation (1.1) is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise. Equation (1.1) is called oscillatory if all its solutions are oscillatory. In recent years, there has been an increasing interest in the study of the problem of determining the oscillation and non-oscillation of solutionsof difference equations of the form (1.1) and its special cases. In[1], Graef et al. proved several theorems provided sufficient conditions foroscillation of all solutions of the third order difference equation of the form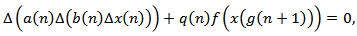
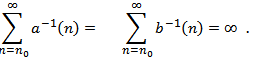
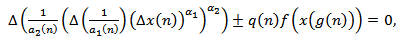
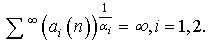
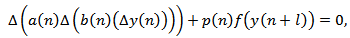
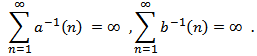
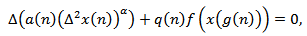
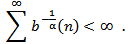
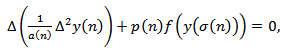
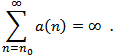
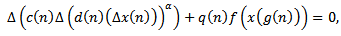
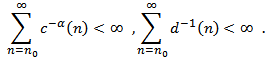
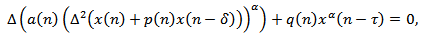
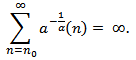
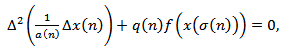
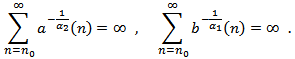
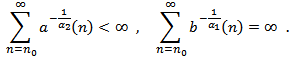
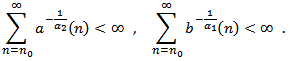
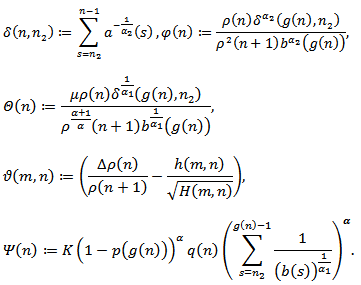 We assume that there exists a double sequence
We assume that there exists a double sequence 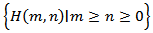 and
and 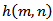 such that
such that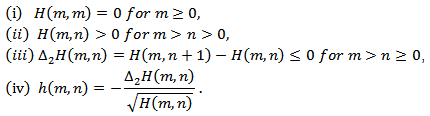 We begin with some useful lemmas, which will be used in obtaining our main results. The proof of the following Lemmas are similar to that of (Lemma 2.1, 2.2 and 2.3 respectively in[13]) and hence the details are omitted.Lemma 2.1. Let
We begin with some useful lemmas, which will be used in obtaining our main results. The proof of the following Lemmas are similar to that of (Lemma 2.1, 2.2 and 2.3 respectively in[13]) and hence the details are omitted.Lemma 2.1. Let 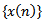 be an eventually positive solution of the equation (1.1) and suppose that
be an eventually positive solution of the equation (1.1) and suppose that 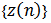 satisfies
satisfies 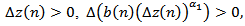
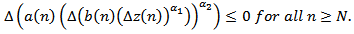 Then there exists
Then there exists 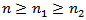 such that
such that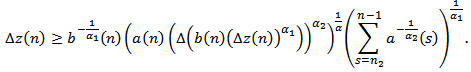
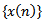 be an eventually positive solution of equation (1.1). Then for sufficiently large
be an eventually positive solution of equation (1.1). Then for sufficiently large 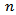 , there are only two possible cases:
, there are only two possible cases: 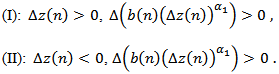 Lemma 2.3. Assume that (2.1) holds. Let
Lemma 2.3. Assume that (2.1) holds. Let 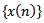 be an eventually positive solution of the equation (1.1) and suppose that Case (II) of Lemma 2.2 holds. If
be an eventually positive solution of the equation (1.1) and suppose that Case (II) of Lemma 2.2 holds. If 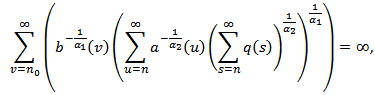
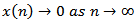 .Theorem 2.1. Let (2.1) and (2.5) hold. If the first order delay equation
.Theorem 2.1. Let (2.1) and (2.5) hold. If the first order delay equation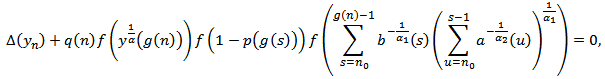
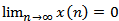 .Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
.Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 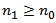 such that
such that 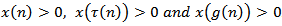 . From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. From Lemma (2.1), we have
. From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. From Lemma (2.1), we have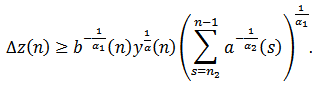 where
where 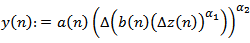 . Summing the above inequality from
. Summing the above inequality from 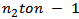 , we obtain
, we obtain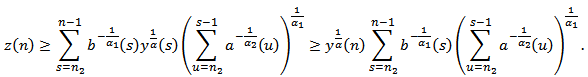
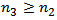 with
with 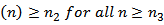 , such that
, such that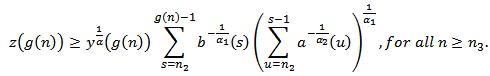
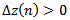 and
and 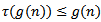 , then
, then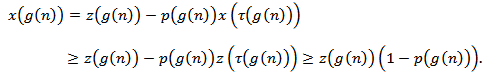
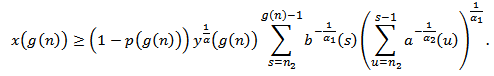 From equation (1.1),
From equation (1.1), 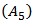 and the last inequality , we obtain,
and the last inequality , we obtain, 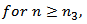
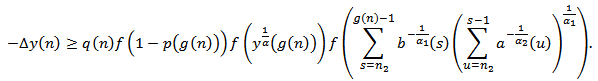 Summing the last inequality from
Summing the last inequality from 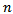 to
to 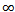 , we get
, we get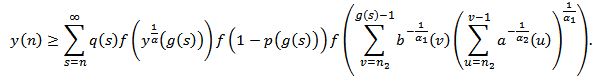 The sequence
The sequence 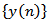 is obviously strictly decreasing. Hence, by the discrete analog of Theorem 1 in[14] we conclude that there exists a positive solution
is obviously strictly decreasing. Hence, by the discrete analog of Theorem 1 in[14] we conclude that there exists a positive solution 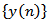 of equation (2.6) which tends to zero. This contradicts that (2.6) is oscillatory. If the (II) holds, we are then back to the proof of Lemma 2.3 to show that
of equation (2.6) which tends to zero. This contradicts that (2.6) is oscillatory. If the (II) holds, we are then back to the proof of Lemma 2.3 to show that 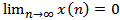 . The proof is complete.Theorem 2.2. Assume that (2.2), (2.5) and (2.6) hold. If
. The proof is complete.Theorem 2.2. Assume that (2.2), (2.5) and (2.6) hold. If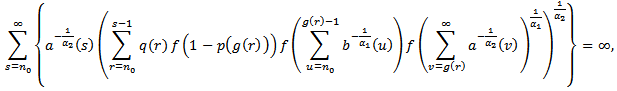
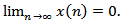 Proof. Let
Proof. Let 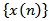 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 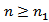 . Say
. Say 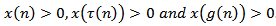 . Based on condition (2.2), there exist three possible cases (I), (II) (as those of Lemma 2.2), and
. Based on condition (2.2), there exist three possible cases (I), (II) (as those of Lemma 2.2), and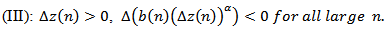 Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 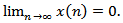 . Assume that (III) holds. Then, we have
. Assume that (III) holds. Then, we have 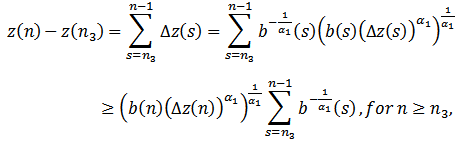 There exists a
There exists a 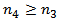 with
with 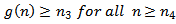 , such that
, such that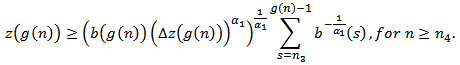 From equation (1.1), (2.9),
From equation (1.1), (2.9), 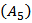 and the last inequality, we obtain,
and the last inequality, we obtain, 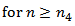
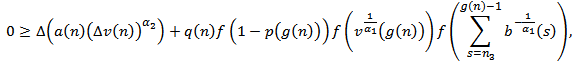
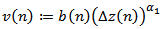 . It is clear that
. It is clear that 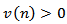 and
and 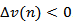 . It follows that
. It follows that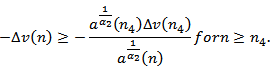 Summing the last inequality from n to
Summing the last inequality from n to 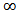 , we obtain
, we obtain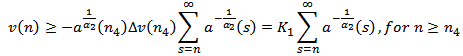 where
where 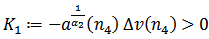 . There exists a
. There exists a 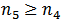 with
with 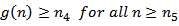 , such that
, such that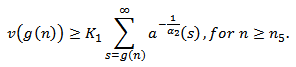 Summing (2.11) from
Summing (2.11) from 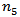 to
to 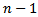 and using the above inequality, we find
and using the above inequality, we find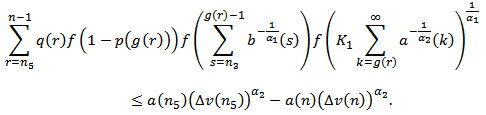 In view of
In view of 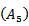 , we see that
, we see that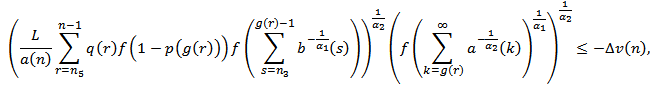 where
where 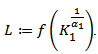 Summing the above inequality from
Summing the above inequality from 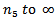 , we obtain
, we obtain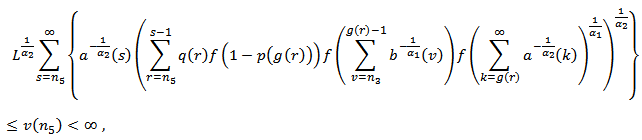 which contradicts the condition (2.10). The proof is complete.Theorem 2.3. Assume that (2.3), (2.5), (2.6) and (2.10) hold. If
which contradicts the condition (2.10). The proof is complete.Theorem 2.3. Assume that (2.3), (2.5), (2.6) and (2.10) hold. If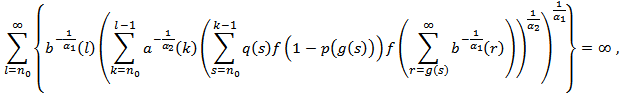
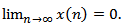 Proof. Let
Proof. Let 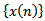 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 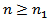 . Say
. Say 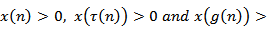
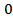 . By (2.3), there exist four possible cases: (I), (II), (III) (as those of Theorem 2.2) and
. By (2.3), there exist four possible cases: (I), (II), (III) (as those of Theorem 2.2) and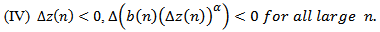 Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.6). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 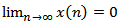 . Assume that (III) holds. Then we are back to the proof of Theorem 2.2 to get contradiction to (2.10). Assume that (IV) holds. We one can choose
. Assume that (III) holds. Then we are back to the proof of Theorem 2.2 to get contradiction to (2.10). Assume that (IV) holds. We one can choose 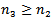 with
with 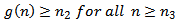 , such that
, such that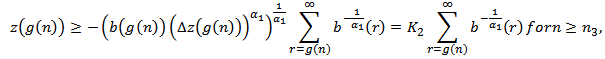 where
where 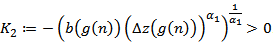 . Thus equation (1.1), (2.9) and
. Thus equation (1.1), (2.9) and 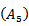 yield
yield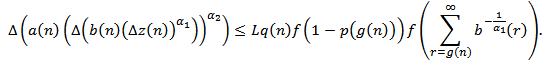 where
where 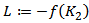 . Summing the above inequality from
. Summing the above inequality from 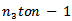 , we find
, we find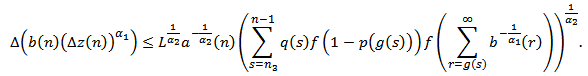 Again summing the above inequality from
Again summing the above inequality from 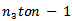 , we find
, we find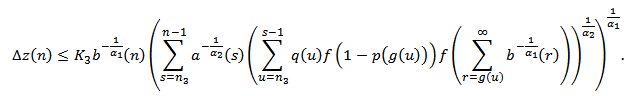 where
where 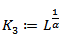 . Finally, summing the above inequality from
. Finally, summing the above inequality from 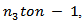 we have
we have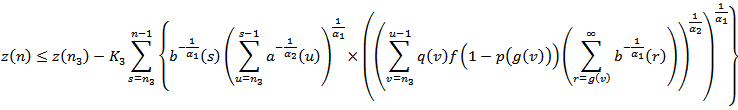 .From condition (2.12), we get
.From condition (2.12), we get 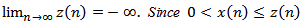 then,
then, 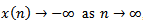 , which contradicts the fact that
, which contradicts the fact that 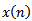 is a positive solution of (1.1). The proof is complete.Theorem 2.4. Let
is a positive solution of (1.1). The proof is complete.Theorem 2.4. Let 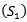 , (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence
, (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence 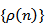 , such that
, such that 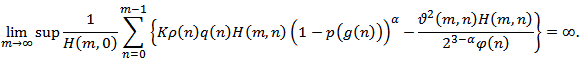
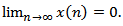 Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 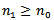 such that
such that 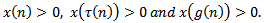 From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence
From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence 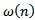 by
by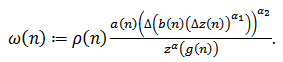
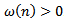 . From (2.14), we have
. From (2.14), we have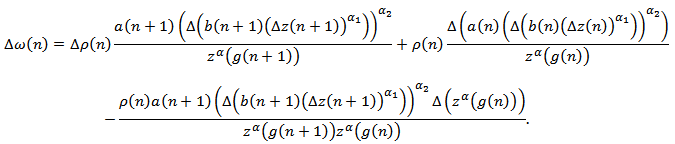 Now, by using the inequality
Now, by using the inequality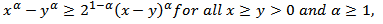
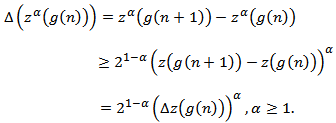 Thus
Thus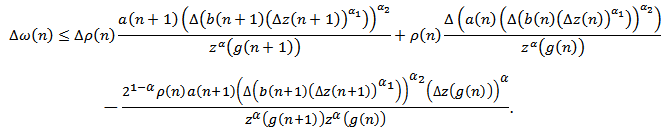
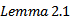 , there exists
, there exists 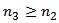 with
with 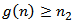 for all
for all 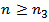 such that
such that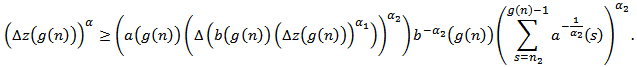
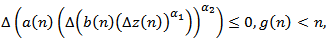 we get
we get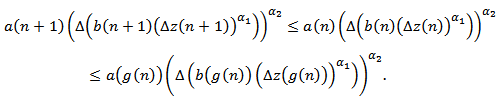
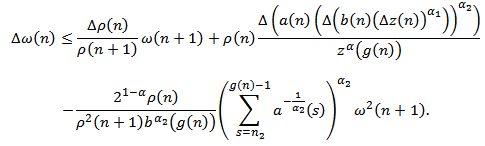 From (2.9), we obtain
From (2.9), we obtain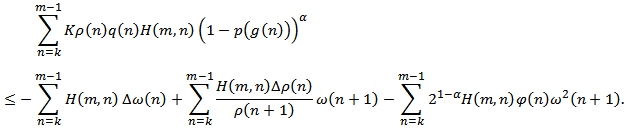 Which yields after summing by parts
Which yields after summing by parts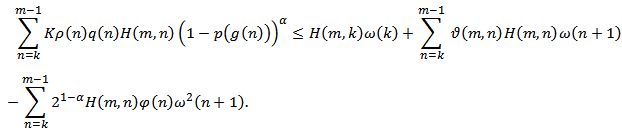 Using the inequality
Using the inequality 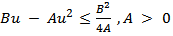 , we have
, we have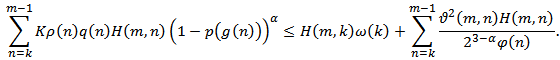
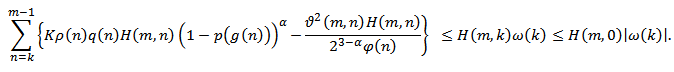 Hence,
Hence,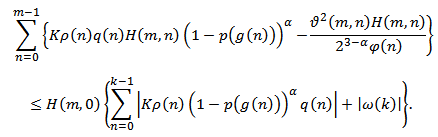 Hence,
Hence,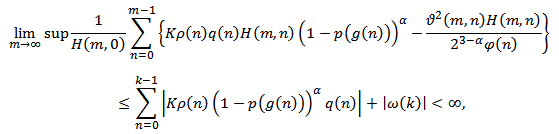 which is contrary to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
which is contrary to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 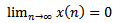 . This completes the proof of Theorem 2.4.Corollary 2.1. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by
. This completes the proof of Theorem 2.4.Corollary 2.1. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by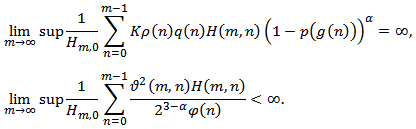 Then equation(1.1) is oscillatory or
Then equation(1.1) is oscillatory or 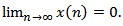 When
When  , we obtain the following resultCorollary 2.2. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by
, we obtain the following resultCorollary 2.2. Assume that all the assumptions of Theorem 2.4 hold, except the condition (2.13) is replaced by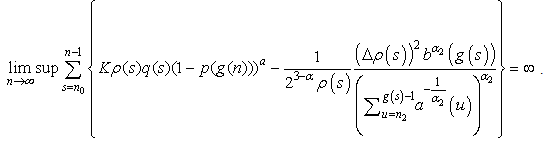
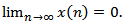 Theorem 2.5. Assume that
Theorem 2.5. Assume that 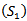 , (2.2), (2.5), and (2.13) hold. If
, (2.2), (2.5), and (2.13) hold. If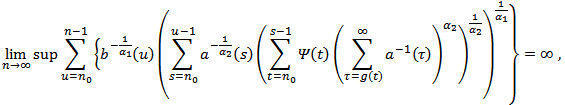
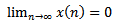 .Proof. Let
.Proof. Let 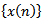 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 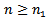 . Say
. Say 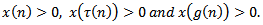 Based on condition (2.2), there exist three possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
Based on condition (2.2), there exist three possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.1 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 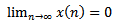 . Assume that (III) holds. Then, there exists
. Assume that (III) holds. Then, there exists 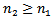 such that
such that 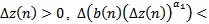
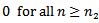 . Then, we have
. Then, we have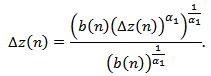 Summing the above inequality from
Summing the above inequality from 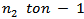 , we obtain
, we obtain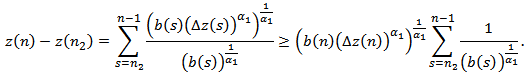
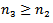 such that
such that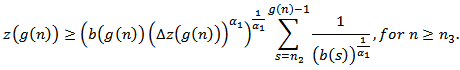 From equation (1.1),
From equation (1.1), 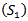 , (2.9) and the last inequality, we obtain
, (2.9) and the last inequality, we obtain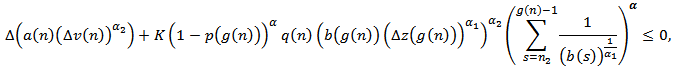
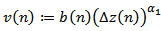 . It is clear that
. It is clear that 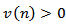 and
and 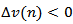 . It follows that
. It follows that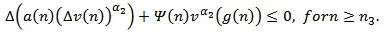
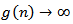 as
as 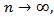 we can choose
we can choose 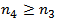 such that
such that 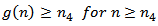 and thus
and thus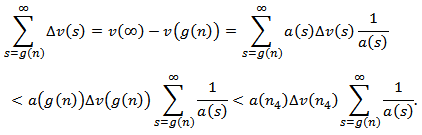 Thus
Thus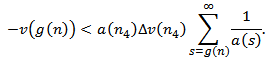 Substituting back in (2.24), we have
Substituting back in (2.24), we have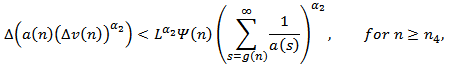
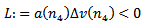 . Summing this inequality from
. Summing this inequality from 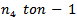 , we see that
, we see that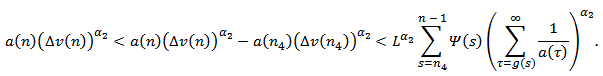 where
where 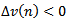 . Summing again from
. Summing again from 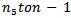 , we have
, we have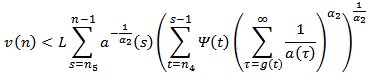 or equivalently
or equivalently 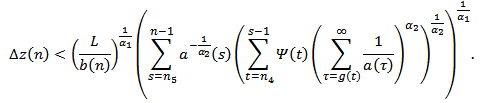 Summing from
Summing from 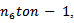 we have
we have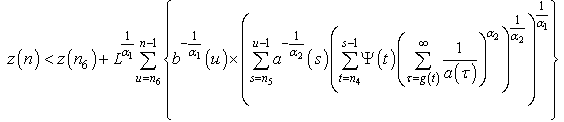 By condition (2.21), we have
By condition (2.21), we have 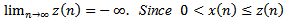 then,
then, 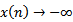 as
as 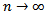 which contradicts the fact that
which contradicts the fact that 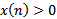 . The proof is complete.Theorem 2.6. Assume that
. The proof is complete.Theorem 2.6. Assume that 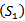 , (2.3), (2.5), (2.13), and (2.21) hold. If
, (2.3), (2.5), (2.13), and (2.21) hold. If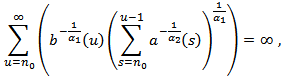
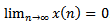 .Proof. Let
.Proof. Let 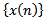 is eventually positive solution of (1.1) for
is eventually positive solution of (1.1) for 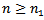 . Based on condition (2.3), there exist four possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.4 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that
. Based on condition (2.3), there exist four possible cases. Assume that (I) holds. Then we are back to the proof of Theorem 2.4 to get contradiction to (2.13). Assume that (II) holds. Then we are back to the proof of Lemma 2.3 to show that 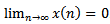 . Assume that (III) holds. Then we are back to the proof of Theorem 2.5 to get contradiction to (2.21). Assume that (IV) holds. Since
. Assume that (III) holds. Then we are back to the proof of Theorem 2.5 to get contradiction to (2.21). Assume that (IV) holds. Since 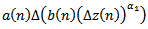 is non-increasing sequence there exists a negative constant
is non-increasing sequence there exists a negative constant 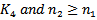 such that
such that 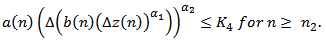 Dividing by
Dividing by 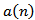 and summing the last inequality from
and summing the last inequality from 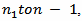 we obtain
we obtain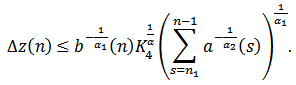 Summing the last inequality from
Summing the last inequality from 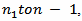 we obtain
we obtain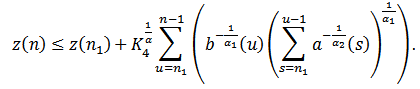 From condition (2.26), we get
From condition (2.26), we get 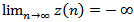 . Since
. Since 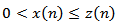 then,
then, 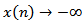 as
as 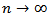 , which contradicts the fact that
, which contradicts the fact that 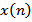 is a positive solution of (1.1). The proof is complete.Theorem 2.7. Let
is a positive solution of (1.1). The proof is complete.Theorem 2.7. Let 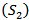 , (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence
, (2.1) and (2.5) hold. Further, assume that thereexists a positive nondecreasing sequence 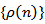 , such that
, such that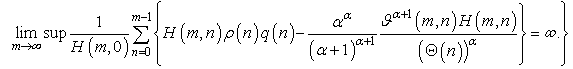
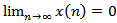 .Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a
.Proof. To the contrary assume that (1.1) has a nonoscillatory solution. Then, without loss of generality, there is a 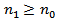 such that
such that 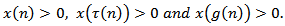 From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence
From the proof of Lemma 2.2 there are two possible cases. Assume that (I) holds. Define the sequence 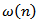 by
by 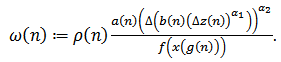
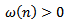 . From (2.28) and
. From (2.28) and 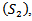 we have
we have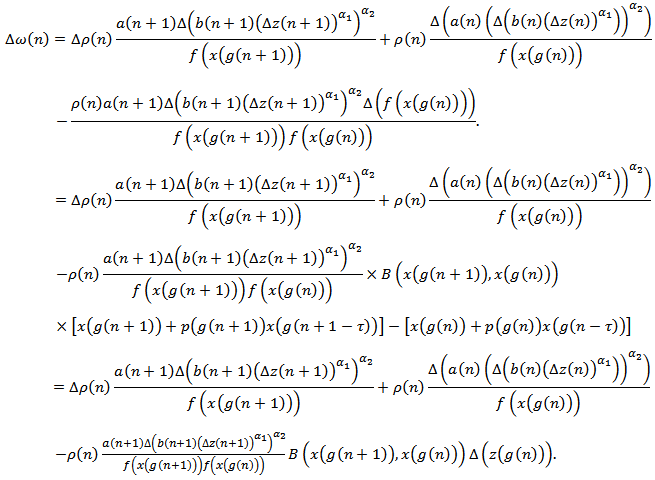
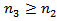 with
with 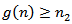 for all
for all 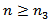 such that
such that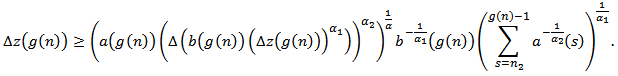
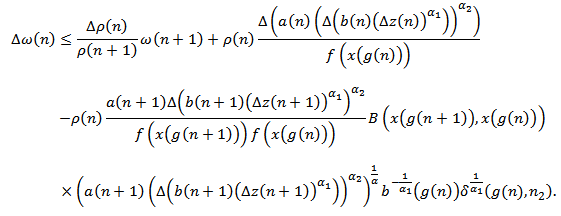
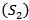 and (2.31), we have
and (2.31), we have 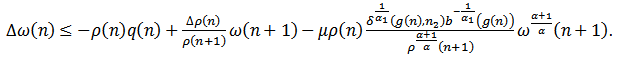
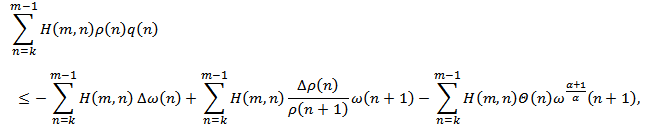 which yields after summing by parts
which yields after summing by parts 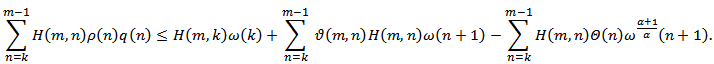 Using the inequality
Using the inequality 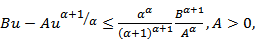 we have
we have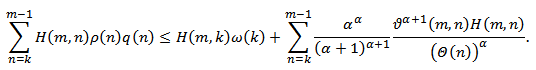 Then,
Then,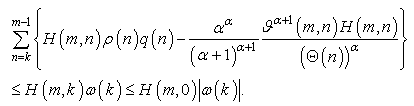 Hence,
Hence,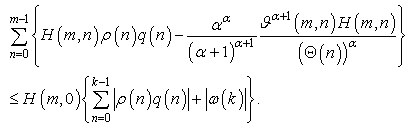 Hence,
Hence,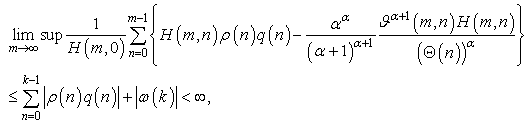 which is contrary to (2.27). Assume that (II)holds. Then we are back to the proof of Lemma 2.3 to show that
which is contrary to (2.27). Assume that (II)holds. Then we are back to the proof of Lemma 2.3 to show that 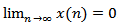 . This completes the proof of Theorem 2.7.From Theorem 2.7, if
. This completes the proof of Theorem 2.7.From Theorem 2.7, if 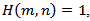 we get the following resultCorollary 2.3. Assume that all the assumptions of Theorem 2.7 hold, except the condition (2.27) is replaced by
we get the following resultCorollary 2.3. Assume that all the assumptions of Theorem 2.7 hold, except the condition (2.27) is replaced by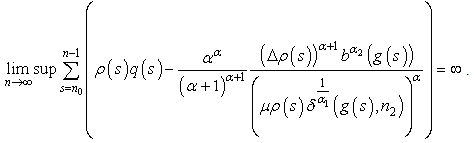 Then equation(1.1) is oscillatory or
Then equation(1.1) is oscillatory or 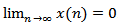 .Theorem 2.8. Assume that (2.2), (2.5), (2.27) and (2.10) hold. Then every solution of equation (1.1) oscillatory or
.Theorem 2.8. Assume that (2.2), (2.5), (2.27) and (2.10) hold. Then every solution of equation (1.1) oscillatory or 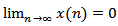 .Proof. The proof is similar to that of Theorem 2.2, Theorem 2.7 and hence the details are omitted.Theorem 2.9. Assume that (2.3), (2.5), (2.27), (2.10) and (2.12) hold. Then every solution of equation (1.1) oscillatory or
.Proof. The proof is similar to that of Theorem 2.2, Theorem 2.7 and hence the details are omitted.Theorem 2.9. Assume that (2.3), (2.5), (2.27), (2.10) and (2.12) hold. Then every solution of equation (1.1) oscillatory or 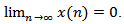 Proof. The proof is similar to that of Theorem 2.3, Theorem 2.7 and hence the details are omitted.
Proof. The proof is similar to that of Theorem 2.3, Theorem 2.7 and hence the details are omitted.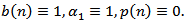 Then Theorem 2.3 reduced to a special case Theorem 2.1 in[4].Remark 3.2. If
Then Theorem 2.3 reduced to a special case Theorem 2.1 in[4].Remark 3.2. If 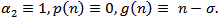 Then Theorem 2.4 extended and improved Theorem 6 in[6].Remark 3.3.
Then Theorem 2.4 extended and improved Theorem 6 in[6].Remark 3.3. 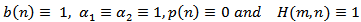 . Then Theorem 2.4 reduced to a special case of Theorem 1 in[5].Remark 3.4. If
. Then Theorem 2.4 reduced to a special case of Theorem 1 in[5].Remark 3.4. If 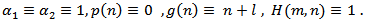 Then Theorem 2.4 extended and improved Theorem 3 in[3].Remark 3.5. If
Then Theorem 2.4 extended and improved Theorem 3 in[3].Remark 3.5. If 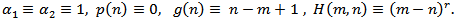 Then Theorem 2.4 reduced to a special case of Theorem 1 in[1].Remark 3.6. If
Then Theorem 2.4 reduced to a special case of Theorem 1 in[1].Remark 3.6. If 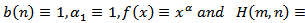 Then Theorem 2.4 extended and improved Theorem 2.7 and Theorem 2.8 in[7].Remark 3.7. If
Then Theorem 2.4 extended and improved Theorem 2.7 and Theorem 2.8 in[7].Remark 3.7. If 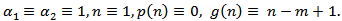 Then Corollary 2.2 reduced to a special case of Theorem 2 in[1].Remark 3.8. If
Then Corollary 2.2 reduced to a special case of Theorem 2 in[1].Remark 3.8. If 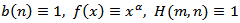 . Then Theorem 2.7 extended and improved Theorem 2.5 and Theorem 2.6 in[7].Remark 3.9. If
. Then Theorem 2.7 extended and improved Theorem 2.5 and Theorem 2.6 in[7].Remark 3.9. If 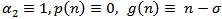 . Then Theorem 2.9 extended and improved Theorem 15 in[6].Remark 3.10. If
. Then Theorem 2.9 extended and improved Theorem 15 in[6].Remark 3.10. If 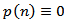 . Then we extended and improved Theorems in[2].Remark 3.11. If
. Then we extended and improved Theorems in[2].Remark 3.11. If 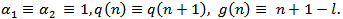 Then we reduced to Theorems in[8].Remark 3.12. If
Then we reduced to Theorems in[8].Remark 3.12. If 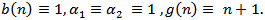 Then we reduced to Theorems in[15].
Then we reduced to Theorems in[15].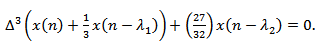
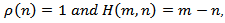 then all conditions of theorem 2.4 are also satisfied. Hence every solution of (4.1) is oscillatory or satisfies
then all conditions of theorem 2.4 are also satisfied. Hence every solution of (4.1) is oscillatory or satisfies 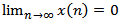 .Example 4.2. Consider the third order nonlinear neutral difference equation
.Example 4.2. Consider the third order nonlinear neutral difference equation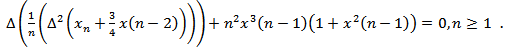
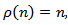 then, Corollary 2.2 asserts that every solution of (4.2) is oscillatory or tend to zero.Example 4.3. Consider the third order difference equationBy choosing
then, Corollary 2.2 asserts that every solution of (4.2) is oscillatory or tend to zero.Example 4.3. Consider the third order difference equationBy choosing 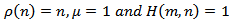 . Then, by Theorem 2.7, we conclude that every solution of (4.3) either oscillates or tend to zero.
. Then, by Theorem 2.7, we conclude that every solution of (4.3) either oscillates or tend to zero. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML