Mohanned Saad Abd Karkosh
Basrah university, Iraq
Correspondence to: Mohanned Saad Abd Karkosh, Basrah university, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The math (DNA) is a new mathematical method which enables us to transform any function into two series, these two series represent the function regarding its mathematical attributes. By extrapolating these two series we can distinguish whether the function is a radical one, a multi-term, fractional or logarithmic ….ext. The characteristic feature of the new method is that we can distribute functions with no need for the function derivative as in Taylor s series method or the differences in the function values as in interpolation. By using the new method we can rewrite the function into two series while the ways mentioned previously cannot give us such results.
Keywords:
Numerical analysis, Math(DNA), Series
Cite this paper: Mohanned Saad Abd Karkosh, Applying the Math (DNA) to Distribute Functions into Series, Applied Mathematics, Vol. 3 No. 5, 2013, pp. 163-170. doi: 10.5923/j.am.20130305.03.
1. Introduction
In formulating the equations of the math (DNA) I used the logarithms and the limit calculation of functions as the independent variable approximates from infinity or from zero. I have adopted several equations to transform functions into two series, for example:-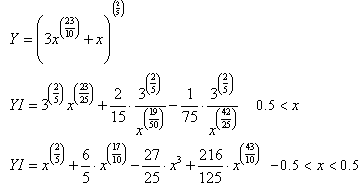
2. The General Structure of the Suggested System
2.1. The Math (DNA) Equations
The following equations are considered to be the basic equations of the math(DNA) which would enable us to find series and they are as follow 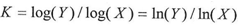 | (1) |
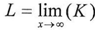 | (2) |
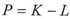 | (3) |
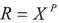 | (4) |
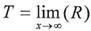 | (5) |
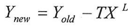 | (6) |
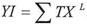 | (7) |
The net result of equations 1-6 is equation number (7).After that we will reuse the seven equations above but when the X approximates from zero so equation number (2) and (5) will be written as follow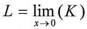 | (2) |
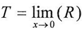 | (5) |
And the summation of equations from (1) to (6) is in the equation (8) as follows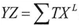 | (8) |
Theory (1)The two series YI and YZ are the math (DNA) for the function Y, or the mathematical code which contains all the mathematical attributes of the function
2.2. Proof
Suppose that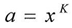 Since
Since 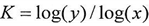 | (1) |
Then 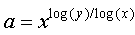 And by taking the logarithm of both sides
And by taking the logarithm of both sides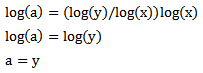 And since
And since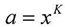 Then
Then 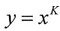 Based on equations (2) and (3), the result will be as follow
Based on equations (2) and (3), the result will be as follow 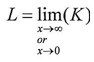 | (2) |
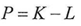 | (3) |
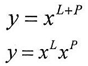 And from equation (4) and (5), y will be equal to
And from equation (4) and (5), y will be equal to 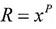 | (4) |
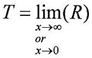 | (5) |
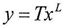 But we cannot consider the equation above always correct because L is the limit of K, and T is the limit of R .where
But we cannot consider the equation above always correct because L is the limit of K, and T is the limit of R .where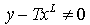 The equation above does not always equal to zero therefore, if the result of subtraction was equal to the following equation then the value of y1 is a new value on which we can apply the equations(1)(2)(3)(4)(5) to find L1 and T1 and then repeating the subtraction process just as we did above. as follow
The equation above does not always equal to zero therefore, if the result of subtraction was equal to the following equation then the value of y1 is a new value on which we can apply the equations(1)(2)(3)(4)(5) to find L1 and T1 and then repeating the subtraction process just as we did above. as follow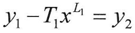 From y2 we can find the value of L2 and T2 by applying the equations (1)-(5) and then using them in the following equation
From y2 we can find the value of L2 and T2 by applying the equations (1)-(5) and then using them in the following equation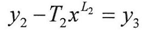 And so on until we reach the following equation
And so on until we reach the following equation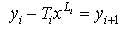 If the value of yi+1 was equal to zero or approximating from zero (which is a value that can be neglected) then the summation of the following equations will produce the following results
If the value of yi+1 was equal to zero or approximating from zero (which is a value that can be neglected) then the summation of the following equations will produce the following results 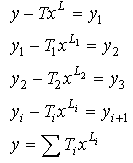 Whereas the summation of the equations above is represented in the final equation which equal to equation (7) of the math (DNA) equations
Whereas the summation of the equations above is represented in the final equation which equal to equation (7) of the math (DNA) equations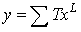 | (7) |
From the final equation we can get tow seriesWhen X approximates from zero we get the following series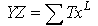 When X approximate from infinity we get the following
When X approximate from infinity we get the following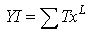 The tow series YZ,YI are the math(DNA) for the function Y
The tow series YZ,YI are the math(DNA) for the function Y
2.3. The Equations of the Math (DNA) According to the Numerical Analysis
Let the following table represent Y=f(X)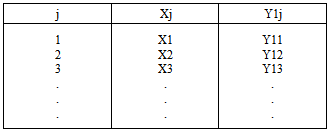 we will apply the math (DNA) equations according to the numerical analysis approach as follow
we will apply the math (DNA) equations according to the numerical analysis approach as follow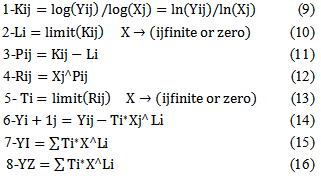 The equations above are applied twice, once when X approximates from zero and once more when X approximates from infinity. there for, we will need another table where the values of X approximate from zero supposing that in the table above the X values approximate from infinity.The following example will explain how would we use the math (DNA) equations according to the numerical analysis approach Example (1)
The equations above are applied twice, once when X approximates from zero and once more when X approximates from infinity. there for, we will need another table where the values of X approximate from zero supposing that in the table above the X values approximate from infinity.The following example will explain how would we use the math (DNA) equations according to the numerical analysis approach Example (1)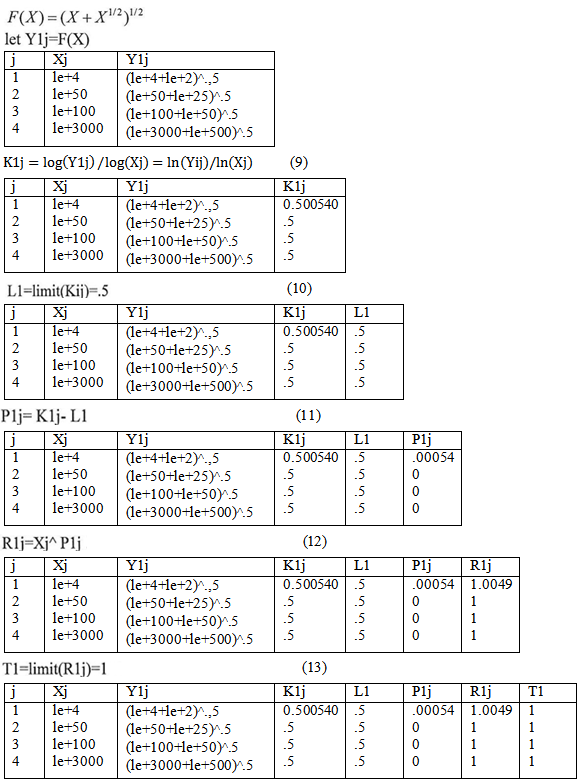 By applying equations (9-15) on the last table repeatedly
By applying equations (9-15) on the last table repeatedly  time after another just as we do previously we will get the following series
time after another just as we do previously we will get the following series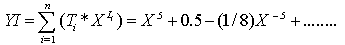 | (15) |
Then apply the new method when X approximates from zero as follow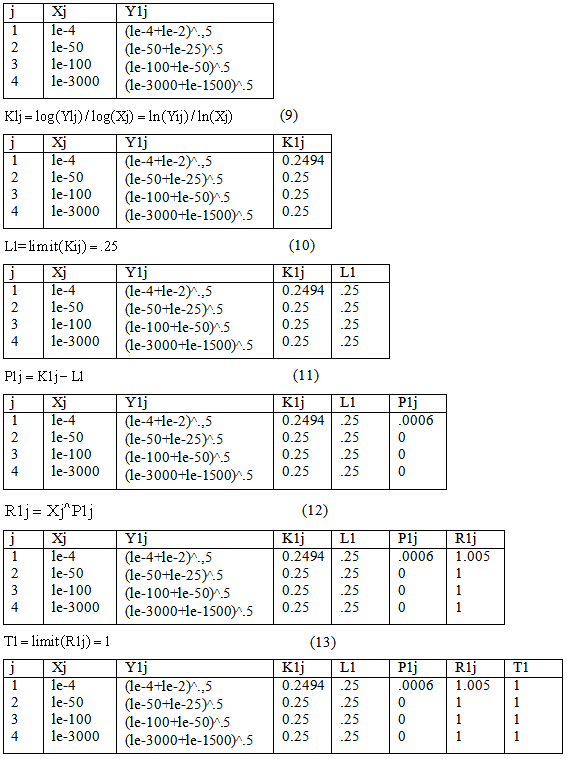
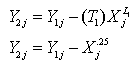 | (14) |
 By applying equations (9-16) on the last table repeatedly time after another just as we do previously we will get the following series
By applying equations (9-16) on the last table repeatedly time after another just as we do previously we will get the following series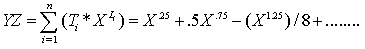 | (16) |
So the math (DNA) for the function (x^.5+x) ^.5 is represented in the following tow series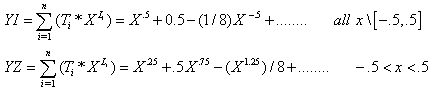
2.4. A MATLAB Program to Calculate the Math (DNA) of the Function
We can notice the complex calculations of tables in the previous example when X approximates from zero and from infinity to find the series which represent the math(DNA) for the function, therefore the following MATLAB program will save us the time and effort that we need for more accuracy to find the math(DNA) of functions The program above calculates the series YI which represent the function Y when X approximates from infinity.The following program is calculating the series YZ which represent the function Y when X approximates from zero
The program above calculates the series YI which represent the function Y when X approximates from infinity.The following program is calculating the series YZ which represent the function Y when X approximates from zero 
2.5. Exploration of the Math(DNA) of Functions
In this part of the research we are going to extract the mathematical attributes of function by using the tow series which represent the math(DNA) of that function.
2.5.1. The Math(DNA) for Multi-term Functions
In multi-term function the two series that represent the math(DNA) of the function will be equal to each other and also equal to the original formula of that function .Proof Suppose the function is equal to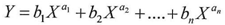 Whereas
Whereas 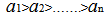 Apply the equations of the math(DNA) on the function Y according to equation (1)
Apply the equations of the math(DNA) on the function Y according to equation (1)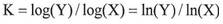 | (1) |
And to calculate L according to equation(2)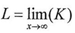 | (2) |
To calculate the limit for the above equation we will apply the hospital rule (3) for limitsWhereas 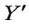 is the first derivative of the function
is the first derivative of the function 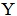
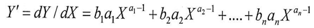 And by substituting the derivative of the function Y in the equation which calculate the limit for K we get
And by substituting the derivative of the function Y in the equation which calculate the limit for K we get 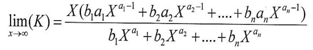 And by simplifying the fraction above we get
And by simplifying the fraction above we get 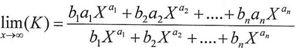 Suppose that
Suppose that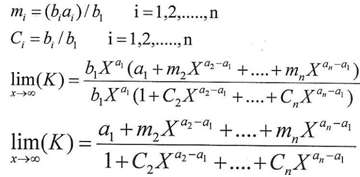 And since
And since 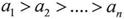 According to the assumptionSo , that will lead to
According to the assumptionSo , that will lead to 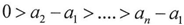 And from the last result we get
And from the last result we get 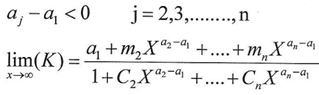 In the fraction above we can notice that X approximates from infinity and that it is raised to a negative exponent which make the final result nearly equal to zero according to the mathematical fact(the inverse of infinity is a value approximating from zero)so we can ignore any X raised to aj-a1 whereas j=2,3,….n.By simplifying the fracture above we get
In the fraction above we can notice that X approximates from infinity and that it is raised to a negative exponent which make the final result nearly equal to zero according to the mathematical fact(the inverse of infinity is a value approximating from zero)so we can ignore any X raised to aj-a1 whereas j=2,3,….n.By simplifying the fracture above we get 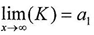 And according to equation (10)
And according to equation (10)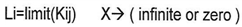 | (10) |
We can notice that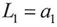 According to equation (11) we get
According to equation (11) we get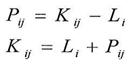 | (11) |
And since 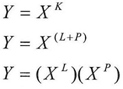 According to equations (12) and (13) we get
According to equations (12) and (13) we get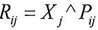 | (12) |
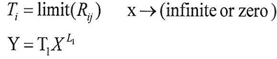 And from the proof
And from the proof 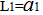
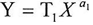 Since
Since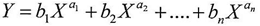 By substituting Y and making several abbreviations
By substituting Y and making several abbreviations 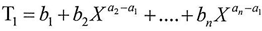 And according to the following (from the proof)
And according to the following (from the proof)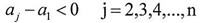 Considering X is approximating from infinity and that it is raised to a negative exponent so the result of this process will be equal to zero resulting in the following
Considering X is approximating from infinity and that it is raised to a negative exponent so the result of this process will be equal to zero resulting in the following 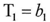 And according to equation (14)
And according to equation (14)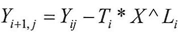 | (14) |
By substitution in the equation above the following will result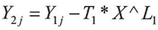 | (14) |
And by substitution in the equation(14) considering Y= Y1j give us Y2j equal to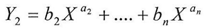 And by using the same steps of the proof we will find that Li=ai ,Ti=bi, i=1,2,3…n and according to equation(15)
And by using the same steps of the proof we will find that Li=ai ,Ti=bi, i=1,2,3…n and according to equation(15)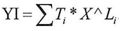 | (15) |
The following result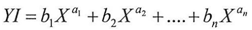 And regarding the second part of the proof, it will be when X approximates from zero
And regarding the second part of the proof, it will be when X approximates from zero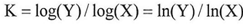 | (1) |
And to calculate the value of L according to equation(2)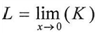 | (2) |
Then we apply the hospital rule(3) to calculate the limit of K when X is approximating from zero 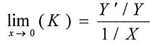 And since
And since 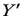 is the first derivative of the function
is the first derivative of the function 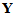
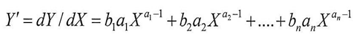 And by substitution the following will result
And by substitution the following will result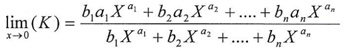 Suppose that
Suppose that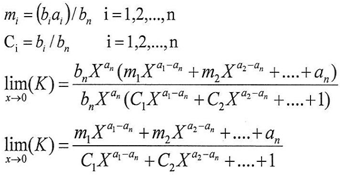 According to the assumption
According to the assumption 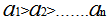 This will lead to
This will lead to In the fraction which calculate the limit of K (mentioned above)we notice that X approximates from zero and that it is raised to positive exponent which make the final result equal to zero and this will lead to the possibility of ignoring any X raised to
In the fraction which calculate the limit of K (mentioned above)we notice that X approximates from zero and that it is raised to positive exponent which make the final result equal to zero and this will lead to the possibility of ignoring any X raised to 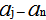 whereas j=1,2,……..n-1 and by simplifying the fraction above we get
whereas j=1,2,……..n-1 and by simplifying the fraction above we get 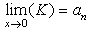 And according to equation (10)
And according to equation (10)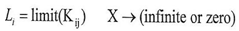 | (10) |
We can notice that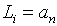 And from equation (11) we get
And from equation (11) we get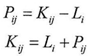 | (11) |
And since 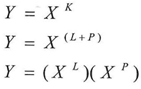 From equation (12) and (13) we get
From equation (12) and (13) we get 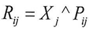 | (12) |
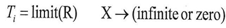 | (13) |
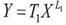 And from the proof
And from the proof 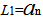
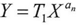 Since
Since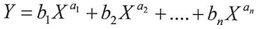 By substitution for Y and making some abbreviations
By substitution for Y and making some abbreviations 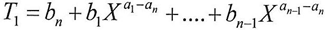 And since X approximates from zero and it is raised to a positive exponent according to the following
And since X approximates from zero and it is raised to a positive exponent according to the following 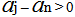 j=1,2,……..n-1 this lead to
j=1,2,……..n-1 this lead to 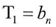 According to equation (14)
According to equation (14)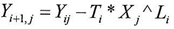 | (14) |
By substitution in the equation above the following result 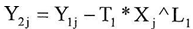 | (15) |
And by substitution in the equation (14) considering Y=Y1j so Y2j will be equal to 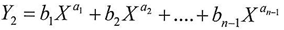 And by the same steps of the proof we can prove that
And by the same steps of the proof we can prove that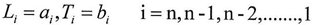 And according to equation(16)
And according to equation(16)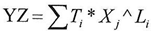 | (16) |
The following result 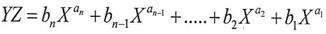 So we can notice the following
So we can notice the following 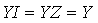 Q.D.
Q.D.
3. The Efficiency of the Suggested System
The math(DNA) system is a process of transforming function into tow series. It characterize by the following:- 1- the result of applying the math(DNA) is two series while the result of the ordinary ways is one series as in interpolation , example :-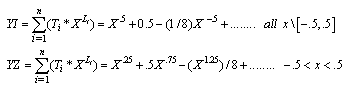 2- the capability of finding the original formula of function by extrapolating the two series which represent that function.3- the incapability of the subordinated ways of finding series for some of the function for example Taylors series while the math (DNA) can find two series whatever the function is complicated.In example(1) at the beginning of research notice that the function Y is equal to the following tow seriesWhereas
2- the capability of finding the original formula of function by extrapolating the two series which represent that function.3- the incapability of the subordinated ways of finding series for some of the function for example Taylors series while the math (DNA) can find two series whatever the function is complicated.In example(1) at the beginning of research notice that the function Y is equal to the following tow seriesWhereas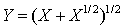 We cannot apply Taylor's series or Maclawrins series on the function mentioned above because we will get no resultNotice:We cannot apply the math(DNA) if there is no limit for K in equation (2) of the math(DNA) equations
We cannot apply Taylor's series or Maclawrins series on the function mentioned above because we will get no resultNotice:We cannot apply the math(DNA) if there is no limit for K in equation (2) of the math(DNA) equations
4. Conclusions
Each function has two series representing the mathematical attributes of it, therefore it resembles the biological DNA of living cell.I expect that more elaboration will be done on the math (DNA) to deal with functions which contain more than one independent variable as in the following functions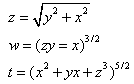 By returning to the subject of extrapolating the math(DNA) we can notice that it is possible to reach the mathematical formula of the function Y if both sides of the math(DNA) were equal, I mean YI=YZ.Therefore I suggest the following equation to represent the general solution for the math (DNA). Let Φ be a function so if Φ(Y) and the tow series which represent the math (DNA) for the function Φ(Y) were ΦI, ΦZ and whereas the tow series were equal ΦI=ΦZ so the original law of the function would be
By returning to the subject of extrapolating the math(DNA) we can notice that it is possible to reach the mathematical formula of the function Y if both sides of the math(DNA) were equal, I mean YI=YZ.Therefore I suggest the following equation to represent the general solution for the math (DNA). Let Φ be a function so if Φ(Y) and the tow series which represent the math (DNA) for the function Φ(Y) were ΦI, ΦZ and whereas the tow series were equal ΦI=ΦZ so the original law of the function would be 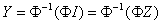
References
| [1] | A-Shield Francis, Schaum Series, 1981, Al Ahram Organization. |
| [2] | B-Al Alosi Dr Ahmad Saleh, Introduction In Neumerical analysis, 1989, The Ministry Of Higher Education And Scientific Researches. |
| [3] | C-Fujideski, The Reference In Higher Mathematics, 1975, Mear press, Moscow. |
| [4] | D-Al Qurmani Dr Ahmed Sadik, Theoretical Mechanic, 1984, Arab House of encyclopedias, Beirut, Lebanon. |
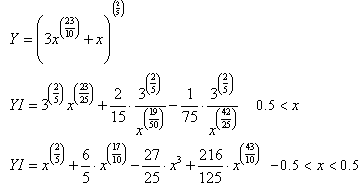
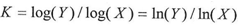
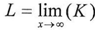
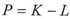
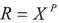
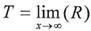
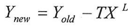
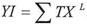
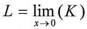
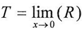
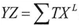
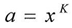 Since
Since 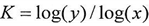
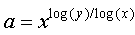 And by taking the logarithm of both sides
And by taking the logarithm of both sides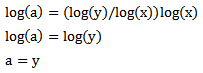 And since
And since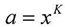 Then
Then 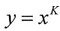 Based on equations (2) and (3), the result will be as follow
Based on equations (2) and (3), the result will be as follow 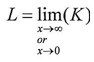
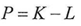
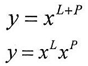 And from equation (4) and (5), y will be equal to
And from equation (4) and (5), y will be equal to 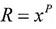
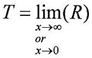
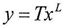 But we cannot consider the equation above always correct because L is the limit of K, and T is the limit of R .where
But we cannot consider the equation above always correct because L is the limit of K, and T is the limit of R .where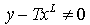 The equation above does not always equal to zero therefore, if the result of subtraction was equal to the following equation then the value of y1 is a new value on which we can apply the equations(1)(2)(3)(4)(5) to find L1 and T1 and then repeating the subtraction process just as we did above. as follow
The equation above does not always equal to zero therefore, if the result of subtraction was equal to the following equation then the value of y1 is a new value on which we can apply the equations(1)(2)(3)(4)(5) to find L1 and T1 and then repeating the subtraction process just as we did above. as follow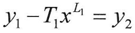 From y2 we can find the value of L2 and T2 by applying the equations (1)-(5) and then using them in the following equation
From y2 we can find the value of L2 and T2 by applying the equations (1)-(5) and then using them in the following equation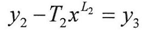 And so on until we reach the following equation
And so on until we reach the following equation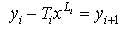 If the value of yi+1 was equal to zero or approximating from zero (which is a value that can be neglected) then the summation of the following equations will produce the following results
If the value of yi+1 was equal to zero or approximating from zero (which is a value that can be neglected) then the summation of the following equations will produce the following results 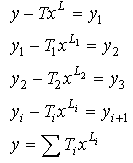 Whereas the summation of the equations above is represented in the final equation which equal to equation (7) of the math (DNA) equations
Whereas the summation of the equations above is represented in the final equation which equal to equation (7) of the math (DNA) equations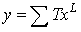
 When X approximate from infinity we get the following
When X approximate from infinity we get the following The tow series YZ,YI are the math(DNA) for the function Y
The tow series YZ,YI are the math(DNA) for the function Y we will apply the math (DNA) equations according to the numerical analysis approach as follow
we will apply the math (DNA) equations according to the numerical analysis approach as follow The equations above are applied twice, once when X approximates from zero and once more when X approximates from infinity. there for, we will need another table where the values of X approximate from zero supposing that in the table above the X values approximate from infinity.The following example will explain how would we use the math (DNA) equations according to the numerical analysis approach Example (1)
The equations above are applied twice, once when X approximates from zero and once more when X approximates from infinity. there for, we will need another table where the values of X approximate from zero supposing that in the table above the X values approximate from infinity.The following example will explain how would we use the math (DNA) equations according to the numerical analysis approach Example (1) By applying equations (9-15) on the last table repeatedly
By applying equations (9-15) on the last table repeatedly  time after another just as we do previously we will get the following series
time after another just as we do previously we will get the following series

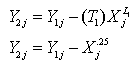
 By applying equations (9-16) on the last table repeatedly time after another just as we do previously we will get the following series
By applying equations (9-16) on the last table repeatedly time after another just as we do previously we will get the following series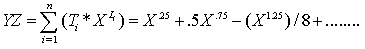
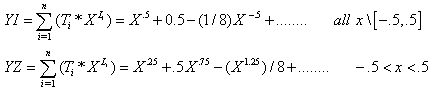
 The program above calculates the series YI which represent the function Y when X approximates from infinity.The following program is calculating the series YZ which represent the function Y when X approximates from zero
The program above calculates the series YI which represent the function Y when X approximates from infinity.The following program is calculating the series YZ which represent the function Y when X approximates from zero 
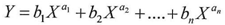 Whereas
Whereas 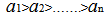 Apply the equations of the math(DNA) on the function Y according to equation (1)
Apply the equations of the math(DNA) on the function Y according to equation (1)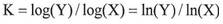
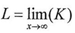
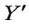 is the first derivative of the function
is the first derivative of the function 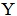
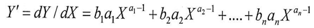 And by substituting the derivative of the function Y in the equation which calculate the limit for K we get
And by substituting the derivative of the function Y in the equation which calculate the limit for K we get 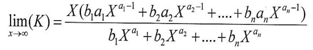 And by simplifying the fraction above we get
And by simplifying the fraction above we get 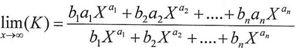 Suppose that
Suppose that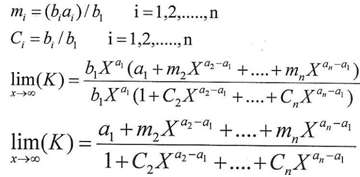 And since
And since 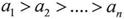 According to the assumptionSo , that will lead to
According to the assumptionSo , that will lead to 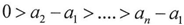 And from the last result we get
And from the last result we get 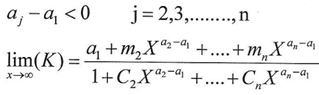 In the fraction above we can notice that X approximates from infinity and that it is raised to a negative exponent which make the final result nearly equal to zero according to the mathematical fact(the inverse of infinity is a value approximating from zero)so we can ignore any X raised to aj-a1 whereas j=2,3,….n.By simplifying the fracture above we get
In the fraction above we can notice that X approximates from infinity and that it is raised to a negative exponent which make the final result nearly equal to zero according to the mathematical fact(the inverse of infinity is a value approximating from zero)so we can ignore any X raised to aj-a1 whereas j=2,3,….n.By simplifying the fracture above we get 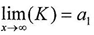 And according to equation (10)
And according to equation (10)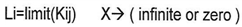
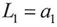 According to equation (11) we get
According to equation (11) we get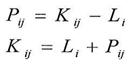
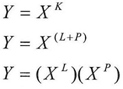 According to equations (12) and (13) we get
According to equations (12) and (13) we get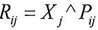
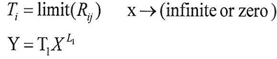 And from the proof
And from the proof 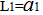
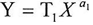 Since
Since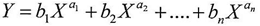 By substituting Y and making several abbreviations
By substituting Y and making several abbreviations 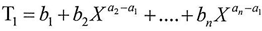 And according to the following (from the proof)
And according to the following (from the proof)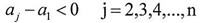 Considering X is approximating from infinity and that it is raised to a negative exponent so the result of this process will be equal to zero resulting in the following
Considering X is approximating from infinity and that it is raised to a negative exponent so the result of this process will be equal to zero resulting in the following 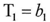 And according to equation (14)
And according to equation (14)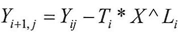
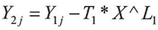
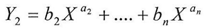 And by using the same steps of the proof we will find that Li=ai ,Ti=bi, i=1,2,3…n and according to equation(15)
And by using the same steps of the proof we will find that Li=ai ,Ti=bi, i=1,2,3…n and according to equation(15)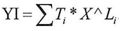
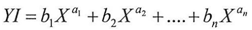 And regarding the second part of the proof, it will be when X approximates from zero
And regarding the second part of the proof, it will be when X approximates from zero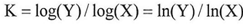
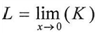
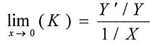 And since
And since 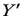 is the first derivative of the function
is the first derivative of the function 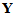
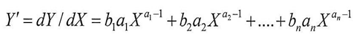 And by substitution the following will result
And by substitution the following will result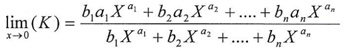 Suppose that
Suppose that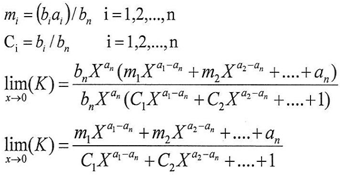 According to the assumption
According to the assumption  This will lead to
This will lead to In the fraction which calculate the limit of K (mentioned above)we notice that X approximates from zero and that it is raised to positive exponent which make the final result equal to zero and this will lead to the possibility of ignoring any X raised to
In the fraction which calculate the limit of K (mentioned above)we notice that X approximates from zero and that it is raised to positive exponent which make the final result equal to zero and this will lead to the possibility of ignoring any X raised to  whereas j=1,2,……..n-1 and by simplifying the fraction above we get
whereas j=1,2,……..n-1 and by simplifying the fraction above we get 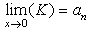 And according to equation (10)
And according to equation (10)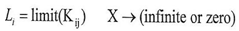
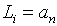 And from equation (11) we get
And from equation (11) we get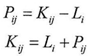
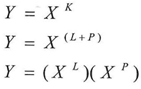 From equation (12) and (13) we get
From equation (12) and (13) we get 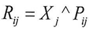
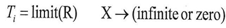
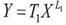 And from the proof
And from the proof 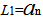
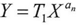 Since
Since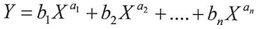 By substitution for Y and making some abbreviations
By substitution for Y and making some abbreviations 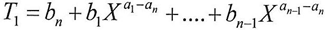 And since X approximates from zero and it is raised to a positive exponent according to the following
And since X approximates from zero and it is raised to a positive exponent according to the following 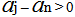 j=1,2,……..n-1 this lead to
j=1,2,……..n-1 this lead to 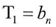 According to equation (14)
According to equation (14)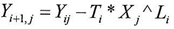
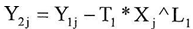
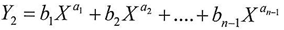 And by the same steps of the proof we can prove that
And by the same steps of the proof we can prove that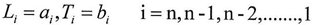 And according to equation(16)
And according to equation(16)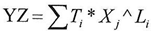
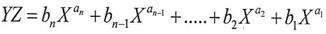 So we can notice the following
So we can notice the following 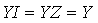 Q.D.
Q.D.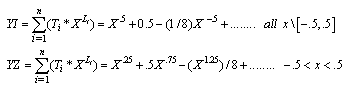 2- the capability of finding the original formula of function by extrapolating the two series which represent that function.3- the incapability of the subordinated ways of finding series for some of the function for example Taylors series while the math (DNA) can find two series whatever the function is complicated.In example(1) at the beginning of research notice that the function Y is equal to the following tow seriesWhereas
2- the capability of finding the original formula of function by extrapolating the two series which represent that function.3- the incapability of the subordinated ways of finding series for some of the function for example Taylors series while the math (DNA) can find two series whatever the function is complicated.In example(1) at the beginning of research notice that the function Y is equal to the following tow seriesWhereas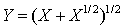 We cannot apply Taylor's series or Maclawrins series on the function mentioned above because we will get no resultNotice:We cannot apply the math(DNA) if there is no limit for K in equation (2) of the math(DNA) equations
We cannot apply Taylor's series or Maclawrins series on the function mentioned above because we will get no resultNotice:We cannot apply the math(DNA) if there is no limit for K in equation (2) of the math(DNA) equations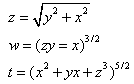 By returning to the subject of extrapolating the math(DNA) we can notice that it is possible to reach the mathematical formula of the function Y if both sides of the math(DNA) were equal, I mean YI=YZ.Therefore I suggest the following equation to represent the general solution for the math (DNA). Let Φ be a function so if Φ(Y) and the tow series which represent the math (DNA) for the function Φ(Y) were ΦI, ΦZ and whereas the tow series were equal ΦI=ΦZ so the original law of the function would be
By returning to the subject of extrapolating the math(DNA) we can notice that it is possible to reach the mathematical formula of the function Y if both sides of the math(DNA) were equal, I mean YI=YZ.Therefore I suggest the following equation to represent the general solution for the math (DNA). Let Φ be a function so if Φ(Y) and the tow series which represent the math (DNA) for the function Φ(Y) were ΦI, ΦZ and whereas the tow series were equal ΦI=ΦZ so the original law of the function would be 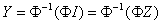
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML