-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2013; 3(4): 152-156
doi:10.5923/j.am.20130304.06
A Proof Method on Labelings of Graph
Zhen-Bin Gao, Wei Qiu, Guang-Yi Sun
College of Science, Harbin Engineering University, Harbin 150001 P.R.China
Correspondence to: Zhen-Bin Gao, College of Science, Harbin Engineering University, Harbin 150001 P.R.China.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Codial labeling and total product cordial labeling of pyramid graph were discussed, and graph decomposition method was introduced. It is proved that pyramid graphs are cordial and total product cordial.
Keywords: Cordial Graph, Total Product Cordial Graph, Pyramid Graph
Cite this paper: Zhen-Bin Gao, Wei Qiu, Guang-Yi Sun, A Proof Method on Labelings of Graph, Applied Mathematics, Vol. 3 No. 4, 2013, pp. 152-156. doi: 10.5923/j.am.20130304.06.
1. Introduction and Definitions
- In1987, Cahit[1] introduced the notion of cordial labeling. Sundaram, Ponraj and Somasundar-am[6] introduced the notions of product cordial labeling and total product cordial labeling in 2006. As for the detailed results on cordial graph, product cordial graph and total product cordial graph, the readers can be referred to[2]. Lee and Wang[4] defined pyramid graph, and proved that pyramid graph is graceful. Most graph labeling methods trace their original one introduced by Rosa[5] in 1967, or one given by Graham and Sloane[3] in 1980. In this paper, graph decomposition method was introduced, it is proved that pyramid graphs are cordial and total product cordial.Definition 1.1.Cordial Graph: a cordial labeling of a graph
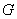 with vertex set
with vertex set 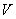 is a function
is a function 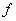 from
from 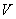 to {0, 1} such that if each edge
to {0, 1} such that if each edge 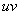 assigned the label
assigned the label 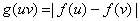 , the number of vertices labeled with 1 and the number of vertices labeled with 0 differ by at most 1, the number of edges labeled with 1 and the number of edges labeled with 0 differ by at most 1. A graph
, the number of vertices labeled with 1 and the number of vertices labeled with 0 differ by at most 1, the number of edges labeled with 1 and the number of edges labeled with 0 differ by at most 1. A graph 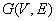 is called cordial graph if it admits a cordial labeling. Definition 1.2. total product cordial graph: a total product cordial labeling of a graph
is called cordial graph if it admits a cordial labeling. Definition 1.2. total product cordial graph: a total product cordial labeling of a graph 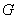 with vertex set
with vertex set 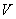 is a function
is a function 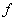 from
from 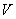 to {0,1} such that if each edge
to {0,1} such that if each edge 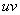 is assigned the label
is assigned the label 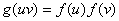 , the number of vertices and edges labeled with 1 and the number of vertices and edges labeled with 0 differ by at most 1. A graph is called total product cordial graph if it admits a total product cordial labeling.Definition 1.3. pyramid graph: a pyramid graph obtained by arranging vertices into a finite number of lines with
, the number of vertices and edges labeled with 1 and the number of vertices and edges labeled with 0 differ by at most 1. A graph is called total product cordial graph if it admits a total product cordial labeling.Definition 1.3. pyramid graph: a pyramid graph obtained by arranging vertices into a finite number of lines with 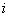 vertices in the
vertices in the 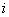 th line and every line the
th line and every line the 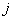 th vertex in that line is joined to the
th vertex in that line is joined to the 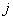 th vertex and the (
th vertex and the (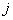 +1)th vertex of the next line. A pyramid graph that has
+1)th vertex of the next line. A pyramid graph that has 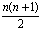 vertices is denoted by
vertices is denoted by 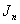 is illustrated in Fig.1.
is illustrated in Fig.1.2. Results
- First, we let
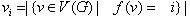 ,
,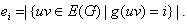 Theorem 2.1.
Theorem 2.1. 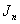 is cordial graph.In the follow discussion,
is cordial graph.In the follow discussion, 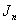 is divided into some subgraphs, and defined the vertex labelings in these subgraphs, to discuss
is divided into some subgraphs, and defined the vertex labelings in these subgraphs, to discuss 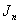 .Proof the vertices of
.Proof the vertices of 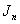 are divided into groups every four lines successively and the vertices in the rest lines (if exists) form one group, in each group, there are odd number of vertices in the first line and the third line, there are even number of vertices in the second line and the fourth line. The rules of vertices in each group are defined as follows:1. the vertex labelings in the same line are alternating
are divided into groups every four lines successively and the vertices in the rest lines (if exists) form one group, in each group, there are odd number of vertices in the first line and the third line, there are even number of vertices in the second line and the fourth line. The rules of vertices in each group are defined as follows:1. the vertex labelings in the same line are alternating 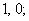 2. the first vertex labeling in the first line and the fourth line are
2. the first vertex labeling in the first line and the fourth line are 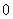 ;3. the first vertex labeling in the second line and the third line are
;3. the first vertex labeling in the second line and the third line are 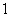 .Based on the previous rules, in every group, the number of vertices labeled with 0 is one more than the number of vertices labeled with 1 in the first line, the number of vertices labeled with 1 is one more than the number of vertices labeled with 0 in the third line, the number of vertices labeled with 0 is the same as the number of vertices labeled with 1 in the second and fourth lines, thereforewhen
.Based on the previous rules, in every group, the number of vertices labeled with 0 is one more than the number of vertices labeled with 1 in the first line, the number of vertices labeled with 1 is one more than the number of vertices labeled with 0 in the third line, the number of vertices labeled with 0 is the same as the number of vertices labeled with 1 in the second and fourth lines, thereforewhen 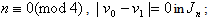 when
when 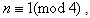 there is only one line in the last group, so
there is only one line in the last group, so 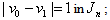
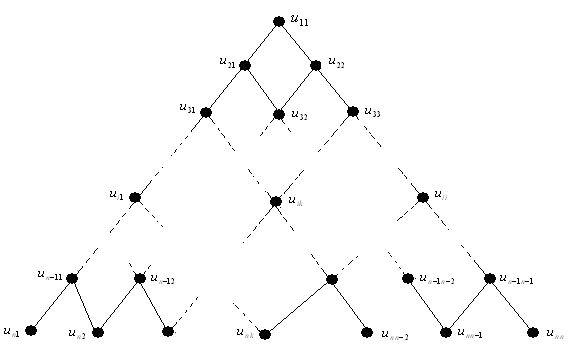 | Figure 1. pyramid  |
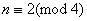 , there are only two lines in the last group, so
, there are only two lines in the last group, so 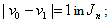 when
when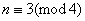 , there are three lines in the last group,
, there are three lines in the last group, 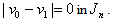 Except the vertices in the last line, each vertex in other lines is adjacent to two vertices in the next line in
Except the vertices in the last line, each vertex in other lines is adjacent to two vertices in the next line in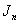 , based on the previous rules and definition 1.1, it is obtained that edge labeled with 0 and 1 which are got between each vertex in each line and adjacent vertices in the next line appear in pairs, so
, based on the previous rules and definition 1.1, it is obtained that edge labeled with 0 and 1 which are got between each vertex in each line and adjacent vertices in the next line appear in pairs, so 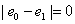 , therefore,
, therefore, 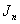 is cordial.Theorem 2.2.
is cordial.Theorem 2.2. 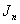 is total product cordial graph.In the follow discussion,
is total product cordial graph.In the follow discussion, 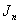 is divided into two part, one is
is divided into two part, one is 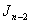 , another is the last two lines in
, another is the last two lines in 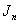 , used the vertex labelings in the last two lines and the total product cordial property of
, used the vertex labelings in the last two lines and the total product cordial property of 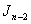 , to discuss
, to discuss 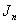 .Lemma 2.1. if
.Lemma 2.1. if 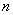 is even, then
is even, then 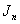 is total product cordial graph.Proof First, the rules are defined as follows:1. the vertex labelings of the first
is total product cordial graph.Proof First, the rules are defined as follows:1. the vertex labelings of the first 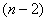 lines in
lines in 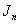 are the vertex labelings in
are the vertex labelings in 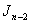 ;2. in
;2. in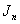 ,the vertex labelings in the odd lines are
,the vertex labelings in the odd lines are 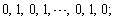 3. when
3. when 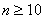 , successive six graphs from one group;4. in
, successive six graphs from one group;4. in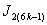 ,the vertex labelings in the last line are
,the vertex labelings in the last line are 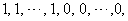 the number of vertices labeled withis
the number of vertices labeled withis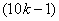 and the number of vertices labeled with
and the number of vertices labeled with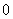 is
is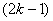 in the last line;5. in
in the last line;5. in 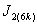 ,the vertex labelings in the last line are
,the vertex labelings in the last line are 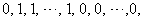 the number of vertices labeled with
the number of vertices labeled with 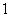 is
is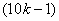 and the number of vertices labeled with
and the number of vertices labeled with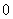 is
is 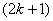 in the last line;6. in
in the last line;6. in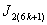 ,the vertex labelings in the last line are
,the vertex labelings in the last line are 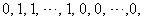 the number of vertices labeled withis
the number of vertices labeled withis 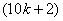 and the number of vertices labeled with
and the number of vertices labeled with 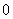 is
is 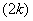 in the last line;7. in
in the last line;7. in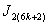 ,the vertex labelings in the last line are
,the vertex labelings in the last line are 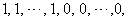 the number of vertices labeled with
the number of vertices labeled with 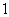 is
is 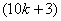 and the number of vertices labeled with
and the number of vertices labeled with 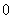 is
is 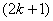 in the last line;8. in
in the last line;8. in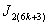 ,the vertex labelings in the last line are
,the vertex labelings in the last line are 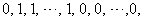 the number of vertices labeled with
the number of vertices labeled with 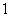 is
is 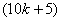 and the number of vertices labeled with
and the number of vertices labeled with 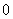 is
is 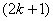 in the last line;9. in
in the last line;9. in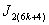 ,the vertex labelings in the last line are
,the vertex labelings in the last line are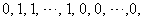 the number of vertices labeled with
the number of vertices labeled with 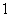 is
is 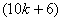 and the number of vertices labeled with
and the number of vertices labeled with 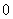 is
is 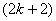 in the last line. The vertex labelings in
in the last line. The vertex labelings in 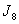 are illustrated in Fig.2, according to the rule
are illustrated in Fig.2, according to the rule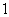 , we obtain that
, we obtain that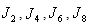 are total product cordial too.
are total product cordial too. 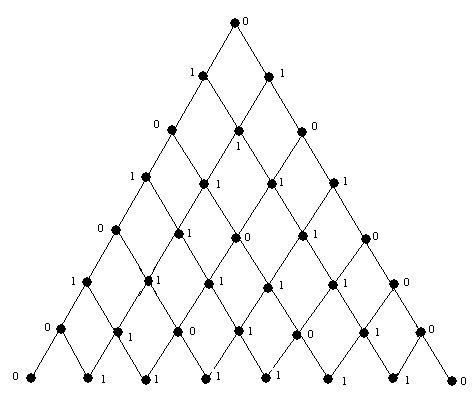 | Figure 2. The vertex labelings in 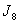 |
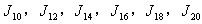 of the first group are discussed as follows. The followings are got by calculation:in
of the first group are discussed as follows. The followings are got by calculation:in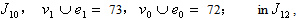
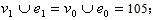 in
in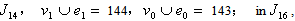
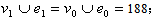 in
in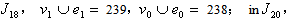
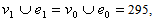 so
so 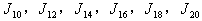 are total product cordial,Suppose,
are total product cordial,Suppose, 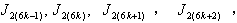
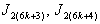 in the
in the 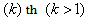 group are total product cordial, the labelings of every graph in the
group are total product cordial, the labelings of every graph in the 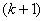 th group are discussed.In
th group are discussed.In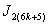 ,according to rule 4, the number of vertices labeled with
,according to rule 4, the number of vertices labeled with 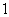 is
is 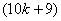 and the number of vertices labeled with
and the number of vertices labeled with 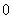 is
is 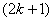 in the last line; according to rule 2, the number of vertices labeled with
in the last line; according to rule 2, the number of vertices labeled with 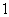 is
is 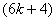 and the number of vertices labeled with
and the number of vertices labeled with 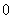 is
is 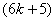 in the second line from the bottom. The numbers of edges labeled with
in the second line from the bottom. The numbers of edges labeled with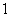 and with
and with 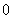 in the last two lines are discussed, because the vertex labelings are alternating
in the last two lines are discussed, because the vertex labelings are alternating 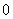 and 1in in the second line from the bottom, the vertex labelings in the third line from the bottom are the vertex labelings in the last line in
and 1in in the second line from the bottom, the vertex labelings in the third line from the bottom are the vertex labelings in the last line in 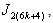 in edges that between the vertices in the third line from the bottom and the vertices in the second line from the bottom, the number of edges labeled with
in edges that between the vertices in the third line from the bottom and the vertices in the second line from the bottom, the number of edges labeled with 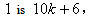 the number of edges labeled with
the number of edges labeled with 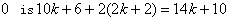 ; in edges that between the vertices in the second line from the bottom and the vertices in the last line, the number of edges labeled with
; in edges that between the vertices in the second line from the bottom and the vertices in the last line, the number of edges labeled with 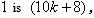 the number of edges labeled with
the number of edges labeled with 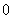 is
is 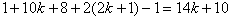 , so the number of vertices and edges labeled with in the last two lines of
, so the number of vertices and edges labeled with in the last two lines of 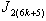 is
is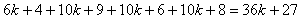 , the number of vertices and edges labeled with
, the number of vertices and edges labeled with 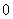 is
is 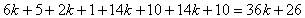 ,because
,because 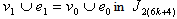 so
so 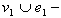
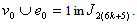 In
In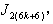 according to rule 5, the number of vertices labeled with
according to rule 5, the number of vertices labeled with 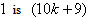 and the number of vertices labeled with
and the number of vertices labeled with 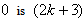 in the last line; according to rule 2, the number of vertices labeled with
in the last line; according to rule 2, the number of vertices labeled with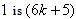 and the number of vertices labeled with
and the number of vertices labeled with 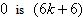 in the second line from the bottom, the vertex labelings in the third line from the bottom are the vertex labelings in the last line in
in the second line from the bottom, the vertex labelings in the third line from the bottom are the vertex labelings in the last line in 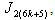 in edges that between the vertices in the third line from the bottom and the vertices in the second line from the bottom, the number of edges labeled with
in edges that between the vertices in the third line from the bottom and the vertices in the second line from the bottom, the number of edges labeled with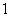 is
is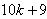 , the number of edges labeled with
, the number of edges labeled with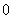 is
is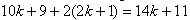 ,similarly, the number of the edges in the last two lines labeled with
,similarly, the number of the edges in the last two lines labeled with 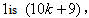 the number of edges in the last two lines labeled with
the number of edges in the last two lines labeled with 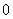 is
is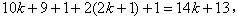 so the number of vertices and edges labeled with in the last two lines of
so the number of vertices and edges labeled with in the last two lines of 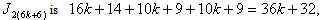 the number of vertices and edges labeled with
the number of vertices and edges labeled with 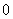 in the last two lines is
in the last two lines is 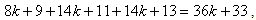 because
because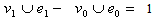 in
in 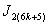 , so
, so 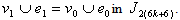 The discussions of labeling number in the next part are similar to the above ones, therefore the number of the labelings of vertices and edges in the last two lines are given as follows.In
The discussions of labeling number in the next part are similar to the above ones, therefore the number of the labelings of vertices and edges in the last two lines are given as follows.In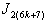 ,according to rule 2 and 6, the number of vertices labeled with
,according to rule 2 and 6, the number of vertices labeled with 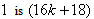 ,the number of vertices labeled with
,the number of vertices labeled with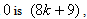 the number of edges labeled with
the number of edges labeled with 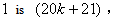 the number of edges labeled with
the number of edges labeled with 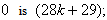 In
In 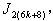 ,according to rule 2 and 7, the number of vertices labeled with
,according to rule 2 and 7, the number of vertices labeled with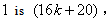 the number of vertices labeled with
the number of vertices labeled with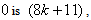 the number of edges labeled with
the number of edges labeled with 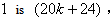 the number of edges labeled with
the number of edges labeled with 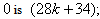 In
In 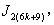 according to rule 2 and 8, the number of vertices labeled with
according to rule 2 and 8, the number of vertices labeled with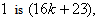 the number of vertices labeled with
the number of vertices labeled with 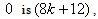 the number of edges labeled with
the number of edges labeled with 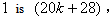 the number of edges labeled with
the number of edges labeled with 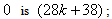 In
In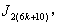 according to rule 2 and 9, the number of vertices labeled with
according to rule 2 and 9, the number of vertices labeled with 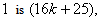 the number of vertices labeled with
the number of vertices labeled with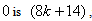 the number of edges labeled with
the number of edges labeled with 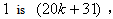 the number of edges labeled with
the number of edges labeled with 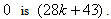 Lemma 2.2. if
Lemma 2.2. if 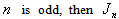 is total product cordial graph.In the proof of lemma 2.2, the discussion is similar to that in lemma2.1, therefore only the rules and some of results in different cases are given.Proof First, the rules are given as follows:1. the vertex labelings in the first
is total product cordial graph.In the proof of lemma 2.2, the discussion is similar to that in lemma2.1, therefore only the rules and some of results in different cases are given.Proof First, the rules are given as follows:1. the vertex labelings in the first 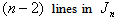 are the vertex labelings in
are the vertex labelings in 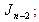 2. in
2. in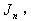 the vertex labelings in the even lines are
the vertex labelings in the even lines are 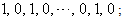 3. when
3. when 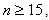 successive six graphs from one group;4. in
successive six graphs from one group;4. in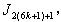 the vertex labelings in the last line are
the vertex labelings in the last line are 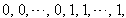 the number of vertices labeled with
the number of vertices labeled with 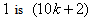 and the number of vertices labeled with
and the number of vertices labeled with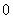 is
is 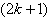 in the last line;5. in
in the last line;5. in 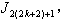 the vertex labelings in the last line are
the vertex labelings in the last line are 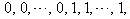 the number of vertices labeled with
the number of vertices labeled with 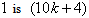 and the number of vertices labeled with
and the number of vertices labeled with 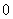 is
is 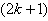 in the last line;6. in
in the last line;6. in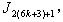 the vertex labelings in the last line are
the vertex labelings in the last line are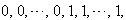 the number of vertices labeled with
the number of vertices labeled with 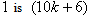 and the number of vertices labeled with
and the number of vertices labeled with 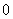 is
is 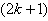 in the last line;7. in
in the last line;7. in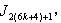 the vertex labelings in the last line are
the vertex labelings in the last line are 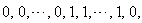 the number of vertices labeled with
the number of vertices labeled with 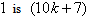 and the number of vertices labeled with
and the number of vertices labeled with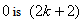 in the last line;8. in
in the last line;8. in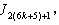 the vertex labelings in the last line are
the vertex labelings in the last line are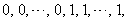 the number of vertices labeled with
the number of vertices labeled with 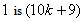 and the number of vertices labeled with
and the number of vertices labeled with 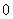 is
is 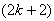 in the last line;9.in
in the last line;9.in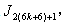 the vertex labelings in the last line are
the vertex labelings in the last line are 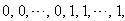 the number of vertices labeled with
the number of vertices labeled with 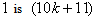 and the number of vertices labeled with
and the number of vertices labeled with 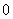 is
is 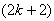 in the last line. The vertex labelings in
in the last line. The vertex labelings in 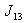 are illustrated in Fig.3. According to rule 1,
are illustrated in Fig.3. According to rule 1, 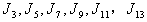 are total product cordial .
are total product cordial .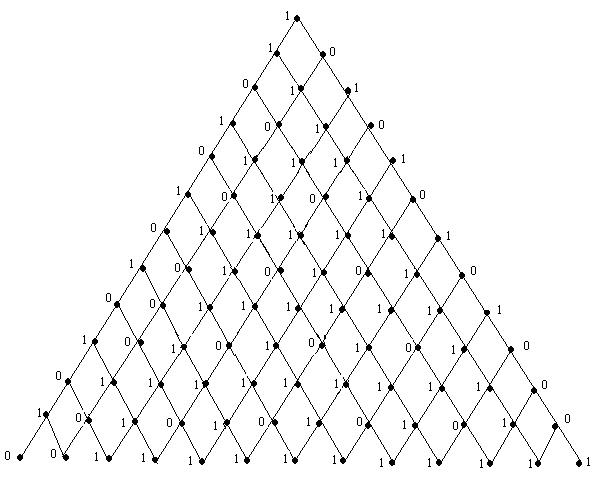 | Figure 3. The vertex labelings in 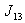 |
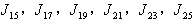 of the first group are discussed as follows. The followings are got by calculation:in
of the first group are discussed as follows. The followings are got by calculation:in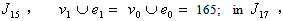
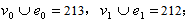 in
in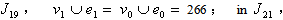
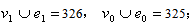 in
in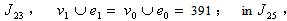
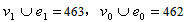 .In
.In 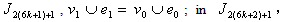
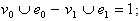 in
in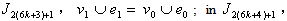
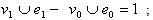 in
in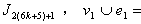
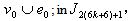
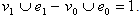 Overall,
Overall, 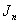 is total product cordial.
is total product cordial.ACKNOWLEDGEMENTS
- The authors would like to thank the anonymous referees very much for valuable suggestions, corrections and comments, which results in a great improvement in the original manuscript.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML