-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2013; 3(4): 144-151
doi:10.5923/j.am.20130304.05
(1,2) - domination in Middle and Central Graph of K1,n, Cn and Pn
N. Murugesan, Deepa. S. Nair
Post Graduate and Research Department of Mathematics Government Arts College, Coimbatore-18, India
Correspondence to: Deepa. S. Nair, Post Graduate and Research Department of Mathematics Government Arts College, Coimbatore-18, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we discuss domination and (1,2) - domination in middle graph and central graph of 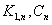 and
and 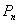 .
.
Keywords: Dominating set, Domination Number, (1,2) - dominating Set, (1,2) - domination Number, Middle Graph, Central Graph
Cite this paper: N. Murugesan, Deepa. S. Nair, (1,2) - domination in Middle and Central Graph of K1,n, Cn and Pn, Applied Mathematics, Vol. 3 No. 4, 2013, pp. 144-151. doi: 10.5923/j.am.20130304.05.
Article Outline
1. Introduction
- Domination in graphs has become an important area of research in graph theory,as evidenced by the many results contained in the two books by Haynes,Hedetniemi and Slater(1998)[6].Vernold Vivin J(2010) have studied the harmonious coloring of line graph, middle graph, central graphs of certain special graphs[12].Venketakrishnan and Swaminathan (2010)[15] have studied the colorclass domination number of middle graph and central graphs of K1,n, Cn and Pn. In this paper we discuss (1,2)-domination in the middle and central graphs of K1,n, Cn and Pn.By a graph
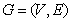 we mean a finite ,undirected graph without loops or multiple edges. A subset
we mean a finite ,undirected graph without loops or multiple edges. A subset 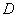 of
of 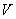 is a dominating set of
is a dominating set of 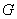 if every vertex of
if every vertex of 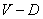 is adjacent to a vertex of
is adjacent to a vertex of 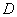 . The domination number of
. The domination number of 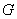 , denoted by
, denoted by 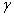 (
(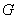 ), is the minimum cardinality of a dominating set of
), is the minimum cardinality of a dominating set of 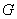 .A (1,2) - dominating set in a graph
.A (1,2) - dominating set in a graph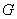 is a set S having the property that for every vertex
is a set S having the property that for every vertex 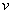 in
in 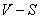 there is atleast one vertex in
there is atleast one vertex in 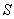 at distance
at distance 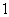 from
from 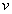 and a second vertex in
and a second vertex in 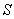 at distance atmost 2 from
at distance atmost 2 from 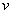 . The order of the smallest (1,2) - dominating set of
. The order of the smallest (1,2) - dominating set of 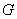 is called the (1,2) - domination number of
is called the (1,2) - domination number of 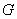 denoted by
denoted by 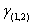 .For a given graph
.For a given graph 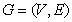 of order n,the central graph
of order n,the central graph 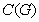 is obtained, by subdividing each edge in E exactly once and joining all the nonadjacent vertices of
is obtained, by subdividing each edge in E exactly once and joining all the nonadjacent vertices of 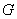 . The central graph
. The central graph 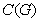 of a graph
of a graph 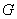 is an example of a split graph, where a split grah is a graph whose vertex set V can be partitioned into two sets, V1 and V2, where every pair of vertices in V1 are adjacent , and no two vertices in V2 are adjacent.The middle graph
is an example of a split graph, where a split grah is a graph whose vertex set V can be partitioned into two sets, V1 and V2, where every pair of vertices in V1 are adjacent , and no two vertices in V2 are adjacent.The middle graph 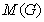 of a graph
of a graph 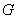 , is the graph whose vertex set is
, is the graph whose vertex set is 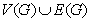 where two vertices are adjacent if and only if they are either adjacent edges of G or one is a vertex and the other is an edge incident with it. That is, two vertices x and y in the vertex set of
where two vertices are adjacent if and only if they are either adjacent edges of G or one is a vertex and the other is an edge incident with it. That is, two vertices x and y in the vertex set of 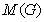 are adjacent in if
are adjacent in if 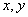 are in
are in 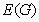 and
and 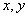 are adjacent in
are adjacent in 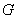 or
or 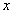 is in
is in 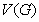 ,y is in
,y is in 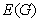 , and x is incident to y in
, and x is incident to y in 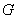 . The related ideas regarding these graphs can be seen in[3,12,13,14].
. The related ideas regarding these graphs can be seen in[3,12,13,14].2. (1,2) - domination in Middle Graphs of K1,n, Cn and Pn.
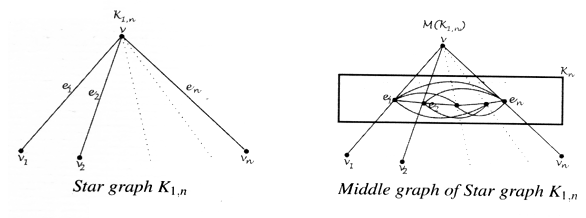
- Theorem 2.1For any star graph
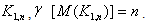 Proof:Let
Proof:Let 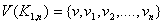 and
and 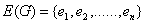 .By the definition of middle graph, we have
.By the definition of middle graph, we have 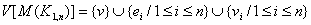 in which the vertices
in which the vertices 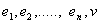 induces a clique of order
induces a clique of order 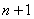 . Hence
. Hence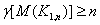 . But
. But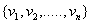 is an independent set and each
is an independent set and each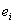 is adjacent to
is adjacent to 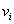 .Therefore
.Therefore 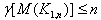 Hence,
Hence, 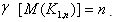
 Theorem 2.2For any star graph
Theorem 2.2For any star graph  (1,2)- domination number
(1,2)- domination number  Proof:Let
Proof:Let  and
and 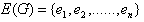 .By the definition of middle graph, we have
.By the definition of middle graph, we have 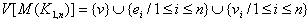 in which the vertices
in which the vertices  induces a clique of order
induces a clique of order 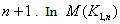 the vertex
the vertex 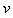 is adjacent to
is adjacent to 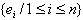 and
and 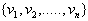 is an independent set and each
is an independent set and each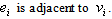 So
So 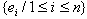 will form a (1,2)- dominating set. That is,
will form a (1,2)- dominating set. That is, 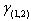
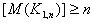 .Since
.Since  induces a clique,
induces a clique, 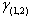
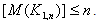 Therefore
Therefore 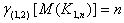 Theorem 2.3For any cycle
Theorem 2.3For any cycle 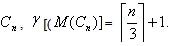 Proof: Let
Proof: Let 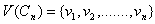 and
and 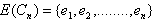 where
where 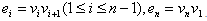 By the definition of middle graph ,
By the definition of middle graph , 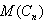 has the vertex set
has the vertex set 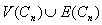 in which each
in which each 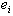 is adjacent with
is adjacent with 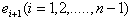 and
and 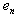 is adjacent with
is adjacent with 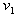 . In
. In 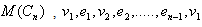 induces a cycle of length
induces a cycle of length 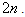 But we know that for
But we know that for 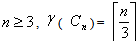 (Theorem 2.1,[5 ]).Thus it is clear that ,
(Theorem 2.1,[5 ]).Thus it is clear that , 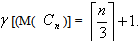 Theorem 2.4For any cycle
Theorem 2.4For any cycle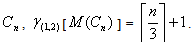 Proof:Let
Proof:Let 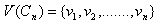 and
and 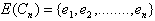 where
where 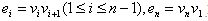 By the definition of middle graph ,
By the definition of middle graph , 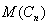 has the vertex set
has the vertex set 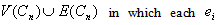 is adjacent with
is adjacent with 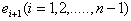 and
and 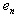 is adjacent with
is adjacent with 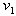 . In
. In 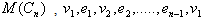 induces a cycle of length
induces a cycle of length 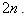 We have by theorem 3.1 in[ 10 ], for any cycle Cn,
We have by theorem 3.1 in[ 10 ], for any cycle Cn, 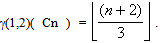 Hence
Hence 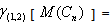
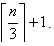 Theorem 2.5For any path
Theorem 2.5For any path 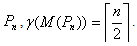 Proof:Let
Proof:Let 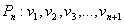 be a path of length
be a path of length 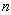 and let
and let 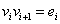 . By the definition of middle graph,
. By the definition of middle graph, 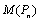 has the vertex set
has the vertex set 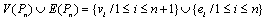 in which each
in which each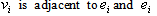 is adjacent to
is adjacent to 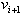 .Also
.Also  Case 1:
Case 1: 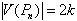 Then. The vertices
Then. The vertices 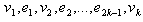 induces a path of length
induces a path of length 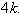 Case 2:
Case 2: 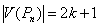 Then
Then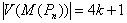 . The vertices
. The vertices 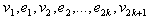 induces a path of length
induces a path of length 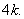 In both the cases,
In both the cases, 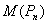 is a path of length
is a path of length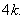 That is,
That is, 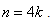 But we have for
But we have for 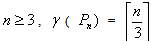 , (Theorem 2.1,[5 ]). Therefore,
, (Theorem 2.1,[5 ]). Therefore, 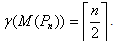 Theorem 2.6For any path
Theorem 2.6For any path 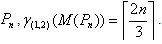 Proof: Let
Proof: Let 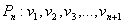 be a path of length
be a path of length 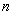 and let
and let 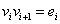 .By the definition of middle graph
.By the definition of middle graph 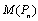 has the vertex set
has the vertex set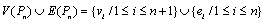 in which each
in which each 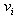 is adjacent to
is adjacent to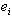 and
and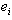 is adjacent to
is adjacent to 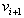 .Also
.Also 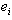 is adjacent to
is adjacent to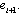 Case 1:
Case 1: 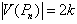 Then
Then 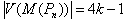 . The vertices
. The vertices  induces a path of length
induces a path of length 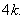 Case 2:
Case 2: 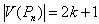 Then
Then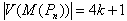 . The vertices
. The vertices 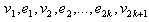 induces a path of length
induces a path of length 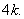 In both the cases,
In both the cases, 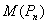 is a path of length
is a path of length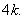 That is,
That is, 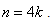 Then by theorem 2.1 in[10] we have
Then by theorem 2.1 in[10] we have 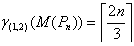
3. (1,2) - domination in Central Graph of K1,n, Cn and Pn.
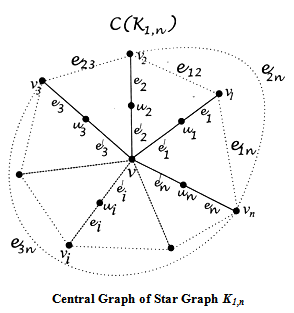
3.1. (1,2)-domination in C(K1,n)
- Theorem 3.1For any star graph
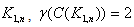 Proof:Let
Proof:Let 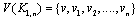 where deg v = n. By the definition of central graph of
where deg v = n. By the definition of central graph of 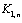 we denote the vertices of subdivision by
we denote the vertices of subdivision by 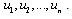 That is, vvi is subdivided by
That is, vvi is subdivided by 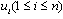 . Let
. Let 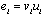 and
and 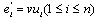 . Therefore
. Therefore 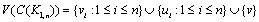 . By the definition of central graph the subgraph induced by the vertex set
. By the definition of central graph the subgraph induced by the vertex set 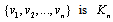 and let eij be the edge of
and let eij be the edge of 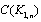 , connecting the vertex vi and vj
, connecting the vertex vi and vj 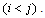
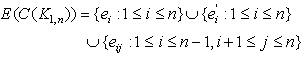 Since in the central graph of a star, the central vertex v together with any one of vi’s form a dominating set. Therefore we have
Since in the central graph of a star, the central vertex v together with any one of vi’s form a dominating set. Therefore we have 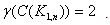
 Theorem 3.2For any star graph
Theorem 3.2For any star graph 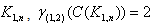 Proof:Let
Proof:Let 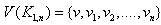 where deg v = n. By the definition of central graph of
where deg v = n. By the definition of central graph of 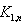 we denote the vertices of subdivision by
we denote the vertices of subdivision by 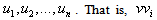 is subdivided by
is subdivided by 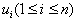 . Let
. Let 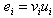 and
and 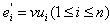 . Therefore
. Therefore 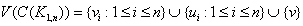 . By the definition of central graph the subgraph induced by the vertex set
. By the definition of central graph the subgraph induced by the vertex set 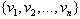 is Kn and let eij be the edge of
is Kn and let eij be the edge of 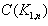 , connecting the vertex vi and vj
, connecting the vertex vi and vj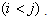 Then
Then 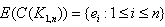
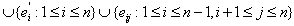 . Since in the central graph of a star, the central vertex of the star is adjacent to every vertex in the central graph the vertex v together with any one of the vetices
. Since in the central graph of a star, the central vertex of the star is adjacent to every vertex in the central graph the vertex v together with any one of the vetices 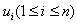 will form a {(1,2)- dominating set. Hence
will form a {(1,2)- dominating set. Hence 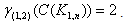
3.2. (1,2)-domination in C(Cn): Consider the Following Examples
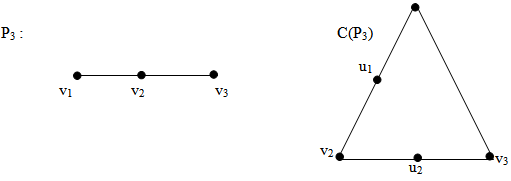
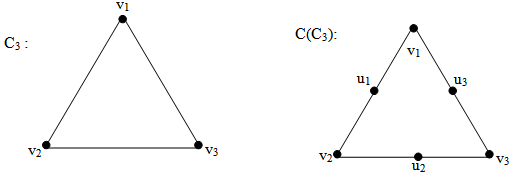 {v1,u2} is a dominating set and also (1,2)-dominating set.
{v1,u2} is a dominating set and also (1,2)-dominating set.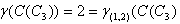
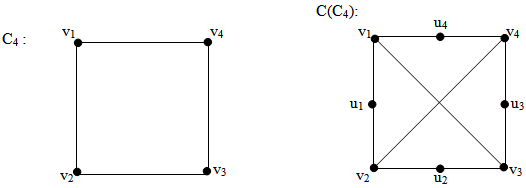 {v1,u2,u3} is a (1,2)-dominating set.
{v1,u2,u3} is a (1,2)-dominating set.
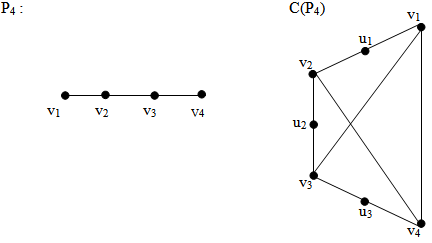
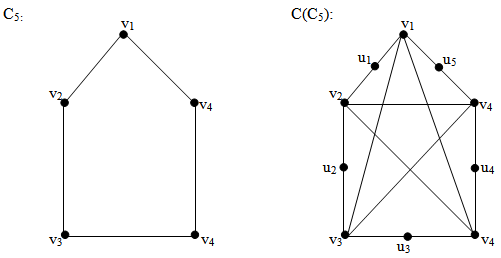 {v1,u2,u3,u4} is a (1,2)-dominating set.
{v1,u2,u3,u4} is a (1,2)-dominating set.
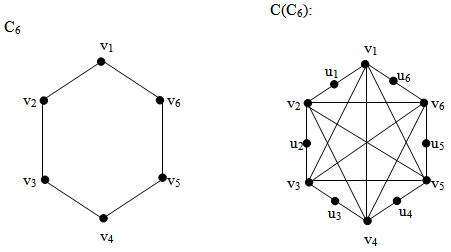 {v1,u2,u3,u4,u5} is a (1,2)-dominating set.
{v1,u2,u3,u4,u5} is a (1,2)-dominating set. Theorem 3.3For any cycle
Theorem 3.3For any cycle  Proof:Let Cn be any cycle of length n and let
Proof:Let Cn be any cycle of length n and let  and
and 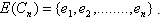 By the definition of central graph
By the definition of central graph 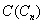 has the vertex set
has the vertex set 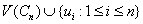 where ui is a vertex of subdivision of the edge vivi+1 (1 ≤ i ≤ n-1) and un is a vertex of subdivision of the edge vnv1. In
where ui is a vertex of subdivision of the edge vivi+1 (1 ≤ i ≤ n-1) and un is a vertex of subdivision of the edge vnv1. In 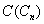 we can note that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except vn-1 and v1.The total number of edges incident with vi is (n-1) for everyi = 1,2,…,n and { ui, (1 ≤ i ≤ n)} is an independent set.So { vi}
we can note that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except vn-1 and v1.The total number of edges incident with vi is (n-1) for everyi = 1,2,…,n and { ui, (1 ≤ i ≤ n)} is an independent set.So { vi}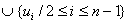 will be a dominating set.So the dominating set will consist of (n-1) vertices.Hence
will be a dominating set.So the dominating set will consist of (n-1) vertices.Hence 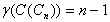 Theorem 3.4For any cycle
Theorem 3.4For any cycle 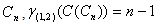 Proof:Let Cn be any cycle of length n and let
Proof:Let Cn be any cycle of length n and let 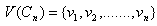 and
and 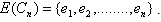 .By the definition of central graph
.By the definition of central graph 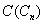 has the vertex set
has the vertex set 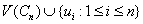 where ui is a vertex of subdivision of the edge vivi+1 (1 ≤ i ≤ n-1) and un is a vertex of subdivision of the edge vnv1. In
where ui is a vertex of subdivision of the edge vivi+1 (1 ≤ i ≤ n-1) and un is a vertex of subdivision of the edge vnv1. In 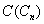 we can note that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except vn-1 and v1.The total number of edges incident with vi is (n-1) for every i = 1,2,…,n and { ui, (1 ≤ i ≤ n)} is an independent set. So { vi}
we can note that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except vn-1 and v1.The total number of edges incident with vi is (n-1) for every i = 1,2,…,n and { ui, (1 ≤ i ≤ n)} is an independent set. So { vi}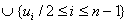 will be a dominating set. But every minimum cardinality dominating set is also a (1,2)-dominating set in
will be a dominating set. But every minimum cardinality dominating set is also a (1,2)-dominating set in 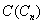 Hence
Hence 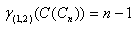
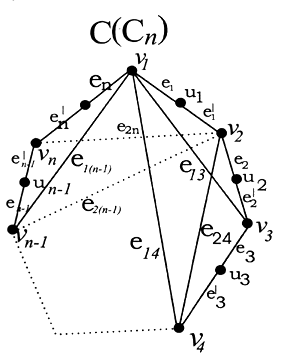
3.3. (1,2)-domination in C(Pn)
 v1,u2} is a dominating set and also (1,2)-dominating set.
v1,u2} is a dominating set and also (1,2)-dominating set. .
. {v1,u2,u3} is a (1,2)-dominating set.
{v1,u2,u3} is a (1,2)-dominating set.
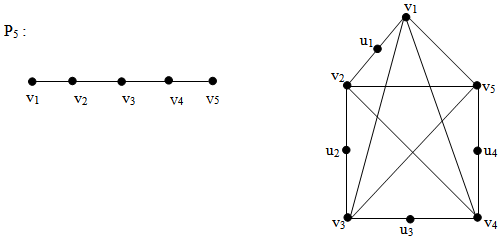 {v1,u2,u3,u4} is a (1,2)-dominating set.
{v1,u2,u3,u4} is a (1,2)-dominating set. Theorem 3.5For any path Pn γ (C(Pn)) = n-1Proof.Let Pn be any path of length n-1 with vertices v1,v2,...........,vn. On the process of centralisation of Pn, let ui be the vertex of subdivision of the edges vivi-1 (1 ≤ i ≤ n).Also let viui=ei and uivi+1=
Theorem 3.5For any path Pn γ (C(Pn)) = n-1Proof.Let Pn be any path of length n-1 with vertices v1,v2,...........,vn. On the process of centralisation of Pn, let ui be the vertex of subdivision of the edges vivi-1 (1 ≤ i ≤ n).Also let viui=ei and uivi+1= 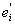 (1 ≤ i ≤ n-1). By the definition of central graph the non-adjacent vertices vi and vj of Pn are adjacent inC(Pn) by the edge eij. Therefore V(C(Pn)) = {vi/1 ≤ i ≤ n} ∪ {ui/1 ≤ i ≤ n-1} and E(C(Pn))={ei :1≤ i ≤ n-1}∪ {
(1 ≤ i ≤ n-1). By the definition of central graph the non-adjacent vertices vi and vj of Pn are adjacent inC(Pn) by the edge eij. Therefore V(C(Pn)) = {vi/1 ≤ i ≤ n} ∪ {ui/1 ≤ i ≤ n-1} and E(C(Pn))={ei :1≤ i ≤ n-1}∪ {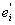 :1≤i≤n-1} ∪ {eij : 1 ≤ i ≤ n -2, i+2 ≤ j ≤ n}. In C(Pn) we can see that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except v2. { ui, (1 ≤ i ≤ n)} is an independent set So
:1≤i≤n-1} ∪ {eij : 1 ≤ i ≤ n -2, i+2 ≤ j ≤ n}. In C(Pn) we can see that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except v2. { ui, (1 ≤ i ≤ n)} is an independent set So 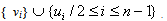 So { vi}
So { vi}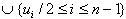 will be a dominating set. γ(C(Pn))= n-1.
will be a dominating set. γ(C(Pn))= n-1.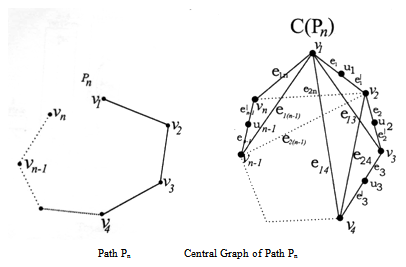 Theorem 3.6For any path Pn,γ(1,2) ((C(Pn))= n-1.Proof:Let Pn be any path of length n-1 with vertices v1,v2,...........,vn. On the process of centralisation of Pn, let ui be the vertex of subdivision of the edges vivi-1 (1 ≤ i ≤ n).Also let viui=ei and uivi+1=
Theorem 3.6For any path Pn,γ(1,2) ((C(Pn))= n-1.Proof:Let Pn be any path of length n-1 with vertices v1,v2,...........,vn. On the process of centralisation of Pn, let ui be the vertex of subdivision of the edges vivi-1 (1 ≤ i ≤ n).Also let viui=ei and uivi+1= 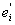 (1 ≤ i ≤ n-1). By the definition of central graph the non-adjacent vertices vi and vj of Pnare adjacent inC(Pn) by the edge eij. Therefore V(C(Pn)) = {vi/1 ≤ i ≤ n} ∪ {ui/1 ≤ i ≤ n-1} and E(C(Pn))={ei :1≤ i ≤ n-1}∪ {
(1 ≤ i ≤ n-1). By the definition of central graph the non-adjacent vertices vi and vj of Pnare adjacent inC(Pn) by the edge eij. Therefore V(C(Pn)) = {vi/1 ≤ i ≤ n} ∪ {ui/1 ≤ i ≤ n-1} and E(C(Pn))={ei :1≤ i ≤ n-1}∪ {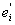 :1≤i≤n-1} ∪ {eij : 1 ≤ i ≤ n -2, i+2 ≤ j ≤ n}. In C(Pn) we can see that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except v2. { ui, (1 ≤ i ≤ n)} is an independent set So
:1≤i≤n-1} ∪ {eij : 1 ≤ i ≤ n -2, i+2 ≤ j ≤ n}. In C(Pn) we can see that the vertex vi is adjacent with all vertices except the vertices vi+1 and vi-1 for 1 ≤ i ≤ n-1.v1 is adjacent with all vertices except v2. { ui, (1 ≤ i ≤ n)} is an independent set So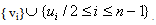 So { vi}
So { vi}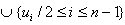 will be a dominating set. γ(C(Pn))= n-1.But every minimum cardinality dominating set of the central graph of a path is also a (1,2)- dominating set. Hence γ(1,2) (C(Pn)) = n-1.
will be a dominating set. γ(C(Pn))= n-1.But every minimum cardinality dominating set of the central graph of a path is also a (1,2)- dominating set. Hence γ(1,2) (C(Pn)) = n-1.4. Relation between Domination Number and (1,2)-domination Number in Middle and Central Graph of Stars, Cycles and Paths
- Theorem 4.1In the middle graph of a star,
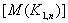 ,the domination number equals the (1,2)-domination number.Proof:This result is obvious from theorem 2.1 and 2.2.Theorem 4.2In the middle graph of cycles,
,the domination number equals the (1,2)-domination number.Proof:This result is obvious from theorem 2.1 and 2.2.Theorem 4.2In the middle graph of cycles,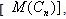 the domination number equals the (1,2)-domination number.Proof:This result is obtained by theorem 2.3 and theorem 2.4.Theorem 4.3In the middle graph of paths,
the domination number equals the (1,2)-domination number.Proof:This result is obtained by theorem 2.3 and theorem 2.4.Theorem 4.3In the middle graph of paths, 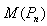 , the domination number is less than or equal to the (1,2)- domination number.Proof:This result is obtained by theorem 2.5 and theorem 2.6. Theorem 4.4In the central graph of any star, C(K1,n), the domination number equalsthe (1,2)-domination number.Proof:This is clear from theorem 3.1 and 3.2.Theorem 4.5In the central graph of cycles, C(Cn), the domination number equals the (1,2)- domination number.Proof:This result is due to the theorem 3.3 and 3.4.Theorem 4.6In the central graph of paths,C(Pn), the domination number equals the (1,2)- domination number.Proof:This result is obtained from theorem 3.5 and 3.6.
, the domination number is less than or equal to the (1,2)- domination number.Proof:This result is obtained by theorem 2.5 and theorem 2.6. Theorem 4.4In the central graph of any star, C(K1,n), the domination number equalsthe (1,2)-domination number.Proof:This is clear from theorem 3.1 and 3.2.Theorem 4.5In the central graph of cycles, C(Cn), the domination number equals the (1,2)- domination number.Proof:This result is due to the theorem 3.3 and 3.4.Theorem 4.6In the central graph of paths,C(Pn), the domination number equals the (1,2)- domination number.Proof:This result is obtained from theorem 3.5 and 3.6.5. Conclusions
- In this paper we have extended (1,2)- domination to the middle graph and central graph of stars, cycles, and paths and discussed both domination and (1,2)- domination number of these graphs. In all cases it is important to see that the domination number is less than or equal to the (1,2)- domination which coincides the result established in[8].
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML