-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2013; 3(4): 132-143
doi:10.5923/j.am.20130304.04
HIV/AIDS Prevalence and Transmission Risks from Mother to Child during the Pregnancy Process in Sub-saharan Africa
Diana Loubaki
Department of Economics, Institut CEDESC, Clamart, 92140, France
Correspondence to: Diana Loubaki, Department of Economics, Institut CEDESC, Clamart, 92140, France.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper investigates the life dynamics properties of pregnant HIV/AIDS infected women with a joint utility function expressing both the mother and her future baby health states during the pregnancy process in Sub-Saharan Africa where medical-care shortages and delays to learn about the infection exist. Non separability of the utility function makes life dynamics oscillate caused by HIV/AIDS prevalence which generates transmission risks of the pandemic to the baby and presents cycles as well as hopf bifurcation while life fluctuates endogenously over time. Applying those results to the Cobb Douglas utility and production functions we find that optimal life dynamics existence and stability depend on illness gravity and medical care investment interaction.
Keywords: HIV/AIDS, Transmission Risk, Infection Gravity,Medical Care, Oscillatory Dynamics, Optimal Path
Cite this paper: Diana Loubaki, HIV/AIDS Prevalence and Transmission Risks from Mother to Child during the Pregnancy Process in Sub-saharan Africa, Applied Mathematics, Vol. 3 No. 4, 2013, pp. 132-143. doi: 10.5923/j.am.20130304.04.
Article Outline
1. Introduction
- This article develops a theoretical model focused on HIV/AIDS acquisition and prevalence in order to establish optimal life dynamics stability when HIV/AIDS transmission risks from mother to child during the pregnancy process exists in Sub-Saharan Africa because of difficulties to fight the pandemic in the area. The analysis deals both with infected and non infected pregnant women where the first deals with optimal growth methods of investigation and the second with oscillatory dynamics methods in order to establish optimal dynamic paths existence and stability since a healthy pregnant woman at her pregnancy beginning time may came out to be infected along her birth gift process. The application of the theory to the Cobb Douglas function highlights a suitable prevention method which shows that optimal life dynamics existence and stability depend on illness gravity and medical care investment interaction. The scientific contribution of this article holds on a unified study of optimal and oscillatory dynamical systems tools in the same growth model applied to the establishment of a steady state in lives dynamics target. Whereas most of the study based on HIV/AIDS in growth models focus on its impact on GDP, human capital accumulation of orphans and labor productivity, this article looks for lives preservation for population growth stability. Finally, the existence of transmission risk possibility of the pandemic along the birth process may create optimal or oscillatory dynamics in Sub-Saharan Africa, thus cycles and hopf bifurcation may appear because the utility function is no more additively separable and no more ensures optimal path existence and stability. The human immunodeficiency virus (HIV) pandemic is one of the most serious health crises the world is facing today. AIDS has killed more than 25 million people since 1981 and an estimated 38.6 million people are now living with HIV, about 2.3 million of them are children[1]. Since 1999, primarily as a result of HIV, average life expectancy has declined in 38 countries. In the most severely affected countries, average life expectancy is now 49 years i.e 13 years less than in the absence of AIDS[2]. A disproportionate burden has been placed on women and children, who in many settings continue to experience high rates of new HIV infections and of HIV-related illness and death. In 2005 alone, an estimated 540 000 children were newly infected with HIV, with about 90% of these infections occurring in Sub-Saharan Africa. Most children living with HIV acquire the infection through mother-to-child transmission (MTCT), which can occur during pregnancy, labor and delivery or during breastfeeding. In the absence of any intervention the risk of such transmission is 15–30% in non-breastfeeding populations. Breastfeeding by an infected mother increases the risk by 5–20% to a total of 20–45%[3]. The risk of MTCT can be reduced to under 2% by interventions that include antiretroviral (ARV) prophylaxis given to women during pregnancy and labor and to the infant in the first weeks of life, obstetrical interventions including elective caesarean delivery (prior to the onset of labor and rupture of membranes), and complete avoidance ofbreastfeeding [4]-[6]. With these interventions, new HIV infections in children are becoming increasingly rare in many parts of the world, particularly in high-income countries where research has focused on more complex regimens and has shown that triple-ARV combinations given to women during pregnancy and labor can reduce the risk of transmission to under 2% [7]-[9]. These regimens are discontinued after childbirth for women without indications for ART (antiretroviral therapy). Since around 1998[10], triple-ARV combinations have increasingly been used to prevent MTCT; currently the majority of pregnant women living with HIV in Europe and North America receive such regimens[11]. In these settings and without breastfeeding, HIV infection in infants has been nearly eliminated. In contrast, Sub-Saharan Africa accounted for 69% of all new infections and nearly half of all HIV-related deaths globally. While 8 million people worldwide can access treatment, nearly 7 million additional people in need of access did not have it as of 2011. Moreover, for every one person on treatment, two are infected. Without effective HIV prevention, the number of people requiring treatment will become unsustainable. Despite the increase in AIDS funding during the past decade, financing gaps persist (International assistance declined from $7.6 billion in 2009 to $6.9 billion in 2010.), and the bulk of likely available funds is unpredictable and mainly for treatment. As new infections rise, country and donor investments in prevention are not being sustained. Efforts are actually targeted for prevention of mother-to-child transmission of HIV, in helping countries accelerate progress on maternal and child health, in line with the 2015 Millennium Development Goals (World Bank Weekly update, November 28, 2012). ARV Drugs treats Pregnant Women and Prevent HIV Infection in Infants are consistent and the Call to Action towards an HIV free and AIDS-free Generation explain the need to study the impact of HIV/AIDS for the case of MTCT in order to develop prevention tools in Sub-Saharan Africa. Therefore, this analysis models the situations of ARV Drugs for Treating Pregnant Women and Preventing HIV infection in Infants to support, the Call to Action Towards an HIV free and AIDS-free Generation. Indeed, the classification made applies pregnant women infected by HIV/AIDS virus investigation methods of oscillating optimal paths where the solution may not exist in growth literature. In the concern of pregnant women where infection is free, optimal stable path can be found because of HIV/AIDS absence. When the mother is infected by HIV/AIDS and may transmit it to the future baby, optimal dynamics oscillates and presents both cycles and Hopf bifurcation at critical points. In that case, the social planner uses the utility function which is no more additively separable but jointly expressed explaining more cares on lives preservation since they are no more submitted to natural birth process (see figures 1 and 2).
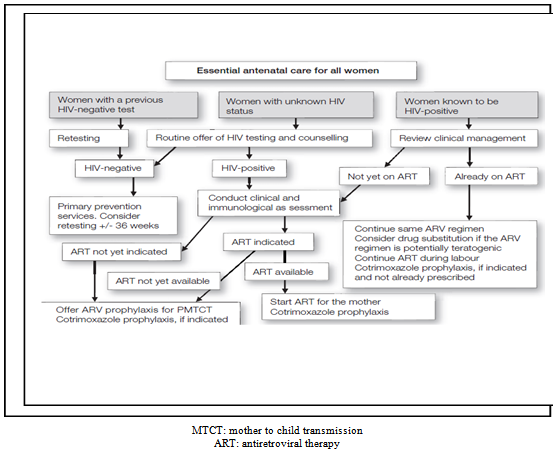 | Figure 1. Comprehensive for the prevention of MTCT: women seen during pregnancy |
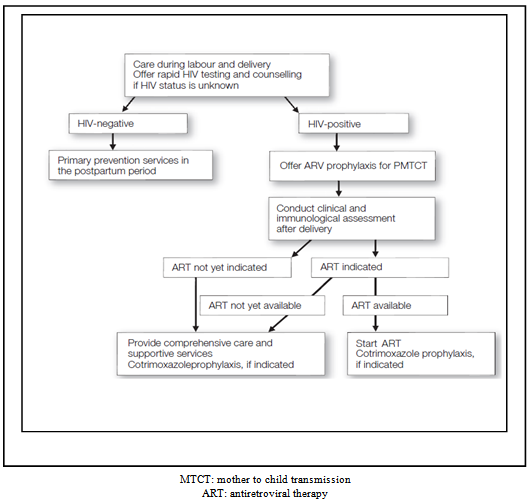 | Figure 2. Comprehensive for the prevention of MTCT: women seen during labour |
2. The Theoretical Model
- This article presents the required tools to study optimal growth and oscillatory dynamics. The first case refers to the healthy future mothers for whom life gift doesn’t fluctuate in contrast to the second case where life has uncertainty character in his gift activity because of HIV/AIDS disease and medical care shortages. We want to understand the way the baby’s life fluctuates endogenously according to his mother’s health state in an economic environment where prevail health care shortages and delays to learn about the infection prevalence in Sub-Saharan Africa.
2.1. The Additively Separable Case: the Non Infected Future Mothers
- This first part presents the theory in the case of per-capita non infected pregnant woman by HIV/AIDS virus denoted stmh whose womb is carrying a baby, st+1ch. The main purpose of the analysis is to present useful tools which allow the study of how the mother's organism can be prevent from the HIV/AIDS virus infection and its transmission to the baby during the pregnancy process. The control is done in order to know if changes outcome i.e if the mother turns out to be infected at a given time during the pregnancy process, then tools control used change to slow the infection gravity in such a way that the pregnancy process reaches its end and ensure that the new born will be healthy and live the required time which is two periods. The pregnancy process takes place during the first period before the birth of the baby who born at the end of that first period and is young during the second period when his mother dies at the end of the second period. The instantaneous utility function
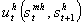 is additively separable in the non HIV/AIDS infection case. The healthy parameters are indexed by h whereas the mother and the child parameters are respectively indexed by m and c.Assumption1: the instantaneous additively separable utility function
is additively separable in the non HIV/AIDS infection case. The healthy parameters are indexed by h whereas the mother and the child parameters are respectively indexed by m and c.Assumption1: the instantaneous additively separable utility function 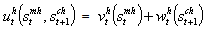 is strictly increasing with respect to each argument i.e
is strictly increasing with respect to each argument i.e 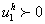 and
and 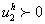 , concave i.e
, concave i.e 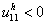 and
and 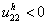 and C2 over the interior of the set Nth (total stock of non infected pregnant women) where
and C2 over the interior of the set Nth (total stock of non infected pregnant women) where 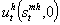 =
= =∞ Optimal strategy for the couple of per-capita mother and her future baby combines the utilities of successive generations in order to guarantee life along the time periods such that:
=∞ Optimal strategy for the couple of per-capita mother and her future baby combines the utilities of successive generations in order to guarantee life along the time periods such that: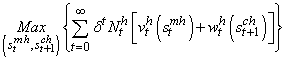 | (2.1) |
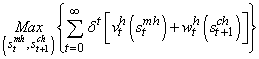 | (2.2) |
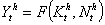 with respect to the following assumption:Assumption 2: The function
with respect to the following assumption:Assumption 2: The function 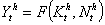 is C² and homogenous of degree 1 with respect to capital stock of drugs produced for the use of, the mother and the future baby's health states include in the interior of the set Nth2.
is C² and homogenous of degree 1 with respect to capital stock of drugs produced for the use of, the mother and the future baby's health states include in the interior of the set Nth2. 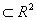 Moreover,
Moreover, 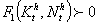 ,
, 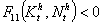 and capital fully depreciates on use along the pregnancy care provision.Assuming that capital fully depreciates on use, per-capita financial constraint in association to life process in the economy is expressed such that:
and capital fully depreciates on use along the pregnancy care provision.Assuming that capital fully depreciates on use, per-capita financial constraint in association to life process in the economy is expressed such that: 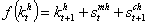 and per-capita stationary capital is determinate by
and per-capita stationary capital is determinate by 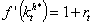 is the return and cost equilibrium relationship i.e
is the return and cost equilibrium relationship i.e 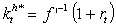 . The expected lives care production function can be expressed in per-capita terms i.e
. The expected lives care production function can be expressed in per-capita terms i.e 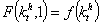 is per-capita healthcare production provided by per-capita investment
is per-capita healthcare production provided by per-capita investment 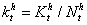 devoted to both the mother and the forthcoming child health states. Thus growth in life expectancy gain is such that
devoted to both the mother and the forthcoming child health states. Thus growth in life expectancy gain is such that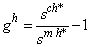 | (2.3) |
2.2. The Non-separable Case
- In this case, per-capita pregnant woman is infected by the virus HIV/AIDS at the beginning time or during her pregnancy process and thus the deal becomes first avoid her death occurrence before the end of the pregnancy time. Second, because her health alteration degree may be higher than expected, medical affords are conducted in a joint way both for the mother and her baby knowing that the mother's health alteration impact on the future baby may be greater than expected due to HIV/AIDS prevalence and transmission susceptibility since medical care requirement is under the needs. Indeed, this case is studied using a non separable utility function and optimal steady state may not exist since the mother's health alteration caused by the pandemic is too great to be saved on time i.e has crossed critical bound allowing the human organism survive until birth outcomes. Thus life dynamics oscillates i.e is uncertain and presents cycles when the virus transmission to the baby is avoid or eventually be chaotic when it is not possible anymore to converge to the steady state and death occurrence is non reversible. Therefore, the goal is to look for necessary existence conditions of a stable equilibrium in life dynamics prevention both for the mother and the baby. In contrast to the previous case, now infections risks for the baby are greater without prevention and treatment. Both the analytical problem and the tools used are more complex and deal with oscillatory dynamics in order to establish optimality conditions at each step.The departure point is financial support equation which remains almost the same than before but now variables are indexed with i (infection) instead of h (healthy). The mother and the child beneficiate from medical treatment supported by a non significant investment i.e
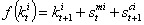 where
where 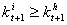 because of more health state damages done by the pandemic inside the body's organism, indeed we have -
because of more health state damages done by the pandemic inside the body's organism, indeed we have -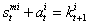 where
where 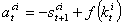 is per-capita future baby inside the womb and means that financial funds support the baby and the mother's health, f(kti) is healthcare provision. Therefore in the next period, the baby’s health evolution follows,
is per-capita future baby inside the womb and means that financial funds support the baby and the mother's health, f(kti) is healthcare provision. Therefore in the next period, the baby’s health evolution follows, 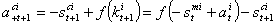 which means that the baby’s stock grows since healthcare quality access is free. In our case, his life depends on his mother's health state in accordance to the virus transmission possibility during the pregnancy. The economic problem can be expressed such that
which means that the baby’s stock grows since healthcare quality access is free. In our case, his life depends on his mother's health state in accordance to the virus transmission possibility during the pregnancy. The economic problem can be expressed such that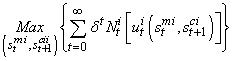 | (2.4) |
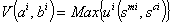 constrained to
constrained to 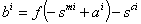 where sci is per-capita future baby carried by a pregnant woman which medical care tries to protect in order to make it becoming a baby at the end of the period, stci=st+1ci is child alive at the beginning of the second period. Using the change of variable such that xi =ai - smi it yields fxi)- sci =bi , the indirect utility function becomes:
where sci is per-capita future baby carried by a pregnant woman which medical care tries to protect in order to make it becoming a baby at the end of the period, stci=st+1ci is child alive at the beginning of the second period. Using the change of variable such that xi =ai - smi it yields fxi)- sci =bi , the indirect utility function becomes: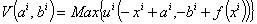 | (2.5) |
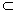 Ei , then ai is the input and bi is the feasible output per young. There exist a level x* such that if 0<xi ≤x* then x*≥f(xi)≥xi. Under those assumptions, let us consider the set:
Ei , then ai is the input and bi is the feasible output per young. There exist a level x* such that if 0<xi ≤x* then x*≥f(xi)≥xi. Under those assumptions, let us consider the set: 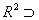 E1i={(ai, bi)ЄEi /
E1i={(ai, bi)ЄEi / 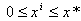 }⊂Ni2 , thus E1i is a compact convex set.Proposition2: If the instantaneous utility function ui(smi, sci) and the production function f(ki) are continuous, increasing and concave, then the indirect utility function V(ai, bi) is concave over E1i The proof if given in[47]Consider the indirect utility function, under the assumptions 1 and 2, the maximum is necessarily interior and is characterized by the first order condition i.e U1(xi*, ai, bi)=0 in the other words we have:
}⊂Ni2 , thus E1i is a compact convex set.Proposition2: If the instantaneous utility function ui(smi, sci) and the production function f(ki) are continuous, increasing and concave, then the indirect utility function V(ai, bi) is concave over E1i The proof if given in[47]Consider the indirect utility function, under the assumptions 1 and 2, the maximum is necessarily interior and is characterized by the first order condition i.e U1(xi*, ai, bi)=0 in the other words we have: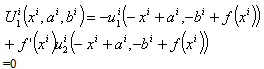 To prove uniqueness of xi* we need to study the concavity with respect to xi* of the function ui(-xi+ai, bi+f(xi)) whose derivative with respect to xi is U1(xi, ai, bi)The second derivative with respect to xi is therefore:
To prove uniqueness of xi* we need to study the concavity with respect to xi* of the function ui(-xi+ai, bi+f(xi)) whose derivative with respect to xi is U1(xi, ai, bi)The second derivative with respect to xi is therefore: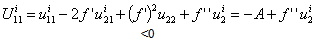 Where:
Where: 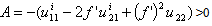 Because of the concavity of u and f then U11i>0 meaning that ui(-xi+ai, -bi+f(xi)) function is not strictly concave with respect to xi therefore, using the implicit function theorem through which we can express x* as a function of ai ,bi i.e xi*(ai ,bi) such that:
Because of the concavity of u and f then U11i>0 meaning that ui(-xi+ai, -bi+f(xi)) function is not strictly concave with respect to xi therefore, using the implicit function theorem through which we can express x* as a function of ai ,bi i.e xi*(ai ,bi) such that: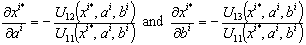 Which expresses analytically such that:
Which expresses analytically such that: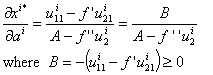
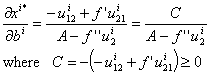 To fully determinate the concavity of the indirect utility function
To fully determinate the concavity of the indirect utility function 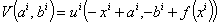 we may compute its second derivatives and use the Shepard lemma through which we obtain
we may compute its second derivatives and use the Shepard lemma through which we obtain 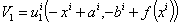 and
and 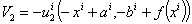 therfore V is a C² function and satisfies:
therfore V is a C² function and satisfies: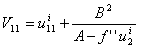 ;
;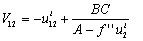
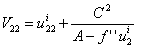 Concavity of V implies V11≤0 and V22≤0 and is verifiedTherefore we clarified using the implicit function theorem that a unique xi* exist and can be written such that xi*=xi*(ai*,bi*), now we need to establish its stability.
Concavity of V implies V11≤0 and V22≤0 and is verifiedTherefore we clarified using the implicit function theorem that a unique xi* exist and can be written such that xi*=xi*(ai*,bi*), now we need to establish its stability.2.3. Study of Local Stability of the Steady State in a Non separable Case
- As in the standard one sector optimal growth models, the stationary capital stock is given by the modified golden rule and doesn't depend on the agents' utility function. Therefore steady state can be expressed such that:
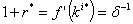 | (2.5) |
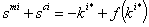 | (2.6) |
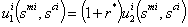 | (2.7) |
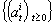 be an optimal sustainable path and let
be an optimal sustainable path and let 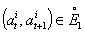 where
where 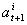 is per-capita baby or new bornIf
is per-capita baby or new bornIf 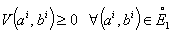 , then the optimal dynamics is monotoneIf
, then the optimal dynamics is monotoneIf 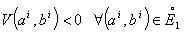 , then the optimal dynamics is oscillatingThe sign of V₁₂ must be evaluated around the steady state neighborhood (ai*, ai*). In our framework, we obtain:Lemma1:
, then the optimal dynamics is oscillatingThe sign of V₁₂ must be evaluated around the steady state neighborhood (ai*, ai*). In our framework, we obtain:Lemma1: 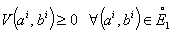 if and only if
if and only if 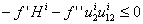 where
where  ≥0 is the determinant of the Hessian matrix of ui evaluated at (smi, sci)PROOF
≥0 is the determinant of the Hessian matrix of ui evaluated at (smi, sci)PROOF
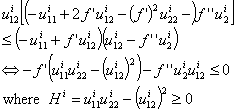 is the determinant of the Hessian matrix of ui evaluated at (smi, sci) and f′=δ⁻¹ The sign of the instantaneous utility function's cross derivative u₁₂i plays a fundamental role. Indeed, if u₁₂i≤0 (or u₁₂i≻0 but not too strong) then V₁₂≽0 (or V₁₂<0) and the dynamics is monotone (or oscillating). We then encompass the separable case, u₁₂i=0 and extend the result to the cases where marginal utility of the babies is a decreasing function i.e death occurrence is coupled with a weakly increasing function of the mothers health state in particular if V₁₂≤0. Finally, if the curvature of the production function is given, an adequate increase of the utility function's degree of concavity may lead to a positive cross derivative V₁₂ and the dynamics is monotone. Thus, there exists a trade-off between the degrees of concavity of f and u. Oscillating paths may be obtained if the production function is more concave than the instantaneous utility function specifically when medical treatment efficiency is less strong than the virus action in health alteration.A sustainable growth in lives path:
is the determinant of the Hessian matrix of ui evaluated at (smi, sci) and f′=δ⁻¹ The sign of the instantaneous utility function's cross derivative u₁₂i plays a fundamental role. Indeed, if u₁₂i≤0 (or u₁₂i≻0 but not too strong) then V₁₂≽0 (or V₁₂<0) and the dynamics is monotone (or oscillating). We then encompass the separable case, u₁₂i=0 and extend the result to the cases where marginal utility of the babies is a decreasing function i.e death occurrence is coupled with a weakly increasing function of the mothers health state in particular if V₁₂≤0. Finally, if the curvature of the production function is given, an adequate increase of the utility function's degree of concavity may lead to a positive cross derivative V₁₂ and the dynamics is monotone. Thus, there exists a trade-off between the degrees of concavity of f and u. Oscillating paths may be obtained if the production function is more concave than the instantaneous utility function specifically when medical treatment efficiency is less strong than the virus action in health alteration.A sustainable growth in lives path: 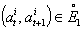 necessarily satisfies the Euler-Lagrange equation i.e
necessarily satisfies the Euler-Lagrange equation i.e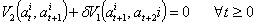 | (2.8) |
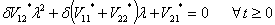 | (2.9) |
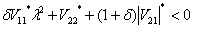 | (2.10) |
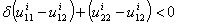 | (2.11) |
 Replacing A,B,C by their respective values, the previous equation becomes
Replacing A,B,C by their respective values, the previous equation becomes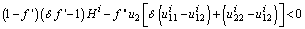 where Hi≥0 Let us consider now the case of oscillating dynamics i.e when V₁₂=-u₁₂i+BC/(A-f′′u₂i)<0 the production function needs to be concave with respect to the instantaneous utility function. We already know that u₁₂(smi, sci)≻0 is a necessary condition for V₂₁<0. Moreover, lemma 1 shows that there exists a trade-off between the degrees of concavity of f and ui. Therefore V₂₁<0 is obtained when the production function is concave with respect to the instantaneous utility function. Therefore we can announce a necessary and sufficient condition for the saddle point property of the steady state. Proposition5: assuming that the instantaneous utility function u₁₂(smi,sci)≻0 and satisfies with the production function condition i.e -f′Hi-f′′u₂ iu₂₂ i≻0 where Hi≥0 is the determinant of the Hessian matrix of ui evaluated at (smi,sci), then the steady state (ai*,ai*) is a regular saddle point if and only if:
where Hi≥0 Let us consider now the case of oscillating dynamics i.e when V₁₂=-u₁₂i+BC/(A-f′′u₂i)<0 the production function needs to be concave with respect to the instantaneous utility function. We already know that u₁₂(smi, sci)≻0 is a necessary condition for V₂₁<0. Moreover, lemma 1 shows that there exists a trade-off between the degrees of concavity of f and ui. Therefore V₂₁<0 is obtained when the production function is concave with respect to the instantaneous utility function. Therefore we can announce a necessary and sufficient condition for the saddle point property of the steady state. Proposition5: assuming that the instantaneous utility function u₁₂(smi,sci)≻0 and satisfies with the production function condition i.e -f′Hi-f′′u₂ iu₂₂ i≻0 where Hi≥0 is the determinant of the Hessian matrix of ui evaluated at (smi,sci), then the steady state (ai*,ai*) is a regular saddle point if and only if: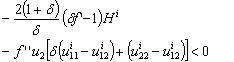 PROOF: under the assumption of the proposition5 i.e u₁₂(smi, sci)≻0 we have V₁₂<0, the condition for the saddle point existence is:
PROOF: under the assumption of the proposition5 i.e u₁₂(smi, sci)≻0 we have V₁₂<0, the condition for the saddle point existence is: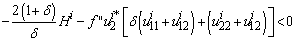 under the assumptions of the proposition we have V12<0, the condition of theorem 1 is
under the assumptions of the proposition we have V12<0, the condition of theorem 1 is 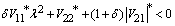 thus,
thus, 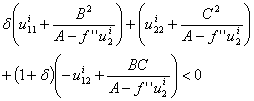 given the values of B, C, A the previous expression is equivalent to
given the values of B, C, A the previous expression is equivalent to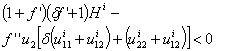 and Since f’=δ⁻¹ and Hi≥0, proposition 5 is verified. Note that if Hi=0, the stability condition becomes
and Since f’=δ⁻¹ and Hi≥0, proposition 5 is verified. Note that if Hi=0, the stability condition becomes 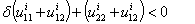
2.4. Flip bifurcation and Competitive Cycles in a Non Separable Case
- Under the assumption of V₁₂<0 we know that optimal paths are oscillating. If the condition of theorem 1 doesn't hold, then there exists a bifurcation value δ* which generates two period cycles. Consequently, if V₁₂<0 we have a flip bifurcation which generates two period cycles.Definition2: δ* is a flip bifurcation value if locally on one side there exist two period cycles and not on the other side. According to assumptions 1 and 2, the saddle point stability provided by theorem 1 is satisfied when δ=1 and leads to the following theorem of Cartigny and Venditti Theorem2: If V₁₂(ai,bi) is strictly negative, then there exist a flip bifurcation value δ*ε(0,1) if and only if the sign of
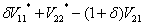 changes when δ crosses δ* Proposition6: Assume that the instantaneous utility function ui is such that ui(smi, sci)≻0 and satisfies with the production function -f′Hi-f′′u₂iu₂₂i≻0 when Hi≥0 is the determinant of the Hessian matrix evaluated at (smi, sci) then there exist a flip bifurcation value δ*ε(0,1) if and only if the sign of:
changes when δ crosses δ* Proposition6: Assume that the instantaneous utility function ui is such that ui(smi, sci)≻0 and satisfies with the production function -f′Hi-f′′u₂iu₂₂i≻0 when Hi≥0 is the determinant of the Hessian matrix evaluated at (smi, sci) then there exist a flip bifurcation value δ*ε(0,1) if and only if the sign of: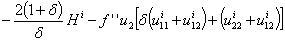 changes when δ crosses δ*. Note that if the instantaneous utility function is not too concave in the neighborhood of the steady state (i.e Hi* is close to zero) whereas the production function is highly concave (i.e |f′′| is high enough), the condition of proposition 5 may be satisfied especially if Hi*=0, the condition becomes, the sign of
changes when δ crosses δ*. Note that if the instantaneous utility function is not too concave in the neighborhood of the steady state (i.e Hi* is close to zero) whereas the production function is highly concave (i.e |f′′| is high enough), the condition of proposition 5 may be satisfied especially if Hi*=0, the condition becomes, the sign of 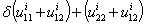 changes when δ crosses δ*
changes when δ crosses δ*3. Application of the Theory
3.1. The Additively Separable Case
- We assume that the non infected pregnant women have an additively separable utility function expressed such that:
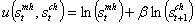 | (3.1) |
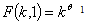 | (3.2) |
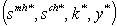 expressed by (3)-(6) i.e
expressed by (3)-(6) i.e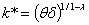 | (3.3) |
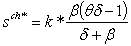 | (3.4) |
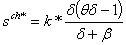 | (3.5) |
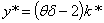 | (3.6) |
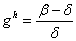 | (3.7) |
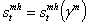 i.e the mother’s health state is conditioned on the pandemic prevalence. Therefore we have
i.e the mother’s health state is conditioned on the pandemic prevalence. Therefore we have 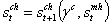 i.e the baby’s health state depends on his mother’s infection gravity. Indeed,
i.e the baby’s health state depends on his mother’s infection gravity. Indeed, 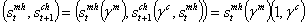 , it is no more possible to separate functionally the mother and the baby variables because for two given scalars λ1 and λ2 , such that
, it is no more possible to separate functionally the mother and the baby variables because for two given scalars λ1 and λ2 , such that 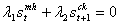 we cannot have λ1 =λ2 =0 for those variables to be expressed freely and taking the utility function we have
we cannot have λ1 =λ2 =0 for those variables to be expressed freely and taking the utility function we have 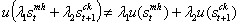 . Indeed
. Indeed 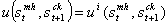 , the additively separable utility function uth(stmh, st+1ch) converges to the non separable utility function uti(stmi, st+1ci) which oscillates in life duration over time.
, the additively separable utility function uth(stmh, st+1ch) converges to the non separable utility function uti(stmi, st+1ci) which oscillates in life duration over time.3.2. The Oscillatory Dynamics
- The utility function is now of Cobb Douglas i.e it is no more additively separable and expressed such that equation (8) i.e:
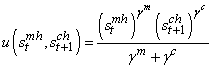 | (3.8) |
 | (3.9) |
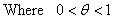 . Using the same formulas as before with
. Using the same formulas as before with 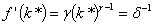 , the stationary values of production, capital stocks and consumptions are expressed such that:
, the stationary values of production, capital stocks and consumptions are expressed such that: 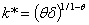 | (3.10) |
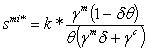 | (3.11) |
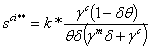 | (3.12) |
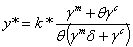 | (3.13) |
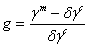 | (3.14) |
3.2.1. Study of the Sign of the Cross Derivative of u
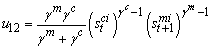 | (3.15) |
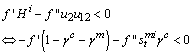 . Therefore, it is necessary to study the sign of V12 in the neighborhood of the steady state. It follows that
. Therefore, it is necessary to study the sign of V12 in the neighborhood of the steady state. It follows that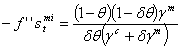 | (3.16) |
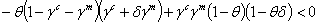
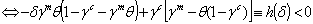 is a monotone decreasing function. Thus depending on the values of γc , γm and θ, if h(1)<0 then V12>0 for all values of the discount factor on (0,1]. Specifically, if θ>γm /1-γc i.e medical care is high, the optimal dynamics is monotone for all values of δ or the economic growth rate, this condition is satisfied only if γc and γm are small enough i.e the utility function is highly concave. Otherwise if medical care is insufficient i.e θ<γm/1-γc , there must be established an optimal economic growth rate δ* such that h(δ*)=0 to ensure population growth stability i.e:
is a monotone decreasing function. Thus depending on the values of γc , γm and θ, if h(1)<0 then V12>0 for all values of the discount factor on (0,1]. Specifically, if θ>γm /1-γc i.e medical care is high, the optimal dynamics is monotone for all values of δ or the economic growth rate, this condition is satisfied only if γc and γm are small enough i.e the utility function is highly concave. Otherwise if medical care is insufficient i.e θ<γm/1-γc , there must be established an optimal economic growth rate δ* such that h(δ*)=0 to ensure population growth stability i.e: 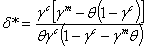 | (3.17) |
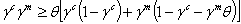 then V12<0 for all values of the discount factor in (0,1] because the system is increasing in per-capita income while population growth is reducing. This condition is also satisfied when γcγm is too high. Otherwise if δ*Є (0,1), the optimal dynamics is monotone only if δЄ(δ*,1]. Then, if the curvature of the production function or health care provision is given, an increase of the utility function’s degree of concavity leads to a positive cross derivative V12. The existence of oscillating paths requires that the production function is concave enough with respect to the instantaneous utility function.
then V12<0 for all values of the discount factor in (0,1] because the system is increasing in per-capita income while population growth is reducing. This condition is also satisfied when γcγm is too high. Otherwise if δ*Є (0,1), the optimal dynamics is monotone only if δЄ(δ*,1]. Then, if the curvature of the production function or health care provision is given, an increase of the utility function’s degree of concavity leads to a positive cross derivative V12. The existence of oscillating paths requires that the production function is concave enough with respect to the instantaneous utility function.3.2.2. Study of Local Stability of the Steady State
- If γcγm<0 , optimal paths are monotone because we have u12<0, it yields:
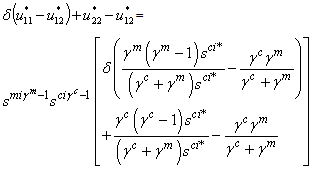 Because
Because 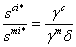 we have
we have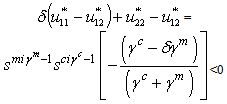 for all δЄ(0,1]. Then, the steady state is a regular saddle point for all values of the discount factor δЄ(0,1]Otherwise, if γcγm>0 and γc+γm ≤1 , the optimal path is oscillating i.e we have u12 >0 and it depends on the concavity properties of f and u. The required condition given in proposition 5 is that
for all δЄ(0,1]. Then, the steady state is a regular saddle point for all values of the discount factor δЄ(0,1]Otherwise, if γcγm>0 and γc+γm ≤1 , the optimal path is oscillating i.e we have u12 >0 and it depends on the concavity properties of f and u. The required condition given in proposition 5 is that 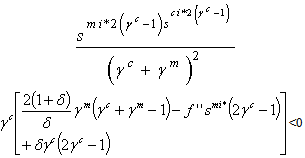 Since γc+γm-1≤0 we conclude that if
Since γc+γm-1≤0 we conclude that if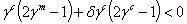 | (3.18) |
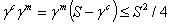 and we obtain
and we obtain 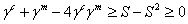 | (3.19) |
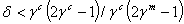 =δ* and it follows from (3.19) that δ*≥1 - If γc<1/2 and γm ≥1/2 with γc+γm≤1 , the sufficient condition becomes δ>δ* i.e economic growth is higher than the equilibrium rate. Indeed the stability condition is satisfied for all δЄ(δ*,1] such that δ*<1In oscillating optimal paths in lives terms, the condition of existence of two periods cycles is given by:
=δ* and it follows from (3.19) that δ*≥1 - If γc<1/2 and γm ≥1/2 with γc+γm≤1 , the sufficient condition becomes δ>δ* i.e economic growth is higher than the equilibrium rate. Indeed the stability condition is satisfied for all δЄ(δ*,1] such that δ*<1In oscillating optimal paths in lives terms, the condition of existence of two periods cycles is given by: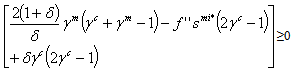 | (3.20) |
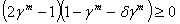 | (3.21) |
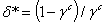 , in contrast to the previous case, now if the utility function is homogenous, cycles may exist for δ close to 1. Indeed, it is sufficient to adequately modify the values of γm toward ½ and then δ* tends toward 1.
, in contrast to the previous case, now if the utility function is homogenous, cycles may exist for δ close to 1. Indeed, it is sufficient to adequately modify the values of γm toward ½ and then δ* tends toward 1.4. Conclusions
- In this paper, we have first proved that in an overlapping generation model with one production sector, if the utility function of health state summarized by per-capita mother and baby is non separable, then optimal steady state in lives terms is not necessarily reached. Depending on the HIV/AIDS gravity and transmission risk and it may appear cycles and hopf bifurcation at critical locus. Applying a specific Cobb Douglas utility function, the event is measured through the comparison between the discount factor which is assimilated to the economic growth rate and population growth of life occurrences view through the HIV/AIDS parameters fluctuations during the pregnancy process. We found that optimal life dynamics existence and stability depend on illness gravity and medical care investment interaction.
ACKNOWLEDGEMENTS
- The author is an experienced researcher in development economics and wishes to thanks the Editor of the journal and the anonymous Referees for helpful comments, errors and misunderstandings are solely mines.
Note
- 1. The function is taken on Michelle-Venditti (1994)
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML