Tanja Van Hecke
University College Ghent, Department of Applied Engineering Sciences, V. Vaerwyckweg 1, B-9000 Ghent, Belgium
Correspondence to: Tanja Van Hecke, University College Ghent, Department of Applied Engineering Sciences, V. Vaerwyckweg 1, B-9000 Ghent, Belgium.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
What makes you win a chess tournament? You should be talented, but the choice of opponents and the applied ranking system will influence your final ranking as well. This article compares different ranking systems (such as the Swiss system and the elimination system) and makes simulations to judge which system is fair. It will lead to a compromise between a qualitative representation of the level of the participants and the length of the tournament or the required number of duels.
Keywords:
Monte-Carlo Simulation, Ranking System, Estimation, Error Function
Cite this paper: Tanja Van Hecke, Monte-Carlo Simulation of Chess Tournament Classification Systems, Applied Mathematics, Vol. 3 No. 4, 2013, pp. 128-131. doi: 10.5923/j.am.20130304.03.
1. Swiss System Versus Elimination System
Many games (chess, bridge, tennis, ...) confront two players. When tournaments take place, many players have to face each other. The way of pairing should lead to a correct classification. A ”Round Robin” is a format of chess tournaments where each opponent plays all of the other opponents. This is the best way of determining playing strength; however, the number of rounds needed are prohibitive for a large number of entrants. For example, for 16 players, there would be 15 rounds using the Round Robin format. Ranking participants at tournaments has been described and discussed from various perspectives[6][7][8][9]. We will develop an evaluation function for ranking methods based on Monte-Carlo simulations. To obtain a representative classification, there exist two main systems: the elimination system and the Swiss system[2][5]. The basic rule for the elimination system is once you lose a round, you fall out and will no longer play. This reduces the number of confrontations between players and is often used in tennis tournaments with infrastructural limitations. The pairing occurs at random at all rounds of the game. Chess tournaments require much less infrastructure. Here the Swiss tournament system is chosen more often. It was invented by J. Muller and first used in a chess tournament at Zurich (Switzerland) in 1895 (hence ”Swiss” system). We assume that players are paired ad random for the starting round. There exist systems where this assumption is replaced by an initial classification based on results of the tournament of the previous year, e.g. the McMahon system. As only the winning players continue, the last round is the most spectacular one where the two best players duel. In the Swiss system the players are classified by the number of games they have won so far. When the number of players is a power of 2, i.e. 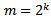 , it is possible to select pairs of players who both won the same number of games, which makes this case the most preferable. We assume one may not play the same player twice within the same tournament.
, it is possible to select pairs of players who both won the same number of games, which makes this case the most preferable. We assume one may not play the same player twice within the same tournament.
2. Tie Breaks
The final classification in the Swiss system is based firstly on the total number of games won by the player. But this doesn't make the players unique and tie breaks will occur. To make a further ranking within the sets 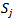 of players who won the same number
of players who won the same number 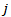 of games, a refinement of the Swiss system is required. Two important tie break methods are the Solkoff method and the cumulative method[3]. The Solkoff method is based on the strength of opponents a player has beaten and is quantified by a weight quantity
of games, a refinement of the Swiss system is required. Two important tie break methods are the Solkoff method and the cumulative method[3]. The Solkoff method is based on the strength of opponents a player has beaten and is quantified by a weight quantity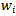 . This weight quantity
. This weight quantity 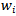 of player
of player 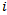 can be defined as the sum of the number of games won by the players beaten by player
can be defined as the sum of the number of games won by the players beaten by player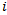 . Within a set
. Within a set 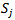 players with higher weights get smaller ranking numbers. For those players with equal weights, the mean of the concerned weight is attributed to each of them. For example: when the ranking numbers 10 and 11 are to be attributed to two players within the same set with equal weights, they are both ranked by number 10.5. The cumulative method is based on the sum
players with higher weights get smaller ranking numbers. For those players with equal weights, the mean of the concerned weight is attributed to each of them. For example: when the ranking numbers 10 and 11 are to be attributed to two players within the same set with equal weights, they are both ranked by number 10.5. The cumulative method is based on the sum 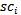 of the cumulative (running) scores for each round of player
of the cumulative (running) scores for each round of player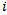 . So if player
. So if player 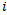 won his first 3 games, lost the fourth game, and won the fifth, his cumulative score is: 1 2 3 3 4. This makes
won his first 3 games, lost the fourth game, and won the fifth, his cumulative score is: 1 2 3 3 4. This makes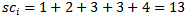 , which would be his cumulative tiebreak. If player
, which would be his cumulative tiebreak. If player 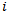 lost his first game, and won the last four, he would have a cumulative tiebreak as follows:
lost his first game, and won the last four, he would have a cumulative tiebreak as follows: 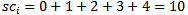 , tiebreak points. The reasoning behind this method is based on the Swiss system of playing an opponent with the same score as oneself. The assumption is that if you win early, you're playing tougher opponents (opponents who also won early and probably finished higher). If you lost in the early rounds, you played weaker opponents (who also lost early and probably didn't finish as high). The higher
, tiebreak points. The reasoning behind this method is based on the Swiss system of playing an opponent with the same score as oneself. The assumption is that if you win early, you're playing tougher opponents (opponents who also won early and probably finished higher). If you lost in the early rounds, you played weaker opponents (who also lost early and probably didn't finish as high). The higher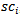 , the better player
, the better player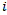 .
.
3. The Game Process
3.1. Simulation Condition
The best way to make a comparative analysis of several ranking methods, is in case the number of players is a power of 2. For example, we consider 16 participants numbered from 1 to 16 with the assumption that the smaller the number, the better the player. This means that when player 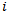 and player
and player 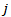 are confronted, player
are confronted, player 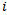 will win if
will win if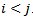 . As the goal of a tournament is to create a classification of players that represents their level, we expect as outcome of the tournament: player
. As the goal of a tournament is to create a classification of players that represents their level, we expect as outcome of the tournament: player 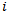 ends up at ranking
ends up at ranking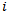 .
.
3.2. Indicating a Winner
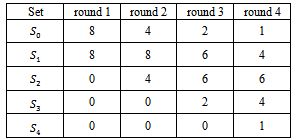
The number of active players in each round is shown in Table 1 for both systems when the tournament starts with 16 players. As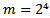 , a winner can be indicated after four rounds.
, a winner can be indicated after four rounds.Table 1. number of players during the different rounds
 |
| |
|
After 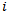 rounds,
rounds, 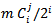 players were able to win
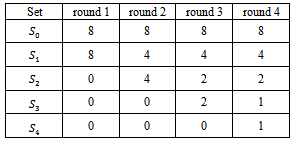
players were able to win 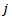 games with the Swiss system, as is shown in Table 3 where the cardinality of the sets
games with the Swiss system, as is shown in Table 3 where the cardinality of the sets 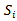 is given at the different stages of the tournament. Here
is given at the different stages of the tournament. Here 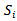 is the set of players who have won
is the set of players who have won 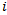 games so far.Table 2 gives analogous cardinalities with the elimination system.
games so far.Table 2 gives analogous cardinalities with the elimination system.Table 2. Cardinality of
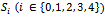 after several rounds with the elimination system after several rounds with the elimination system
 |
| |
|
To compare and evaluate the two basic systems of tournament classification, we simulate the Swiss method without secondary ranking within the sets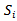 . They all receive the same mean ranking of the set they are in (see Table 4 based on the cardinalities of Table 2 and 3 to determine the mean values). For example, for the Swiss system the ranking 8.5 is assigned to all elements of set
. They all receive the same mean ranking of the set they are in (see Table 4 based on the cardinalities of Table 2 and 3 to determine the mean values). For example, for the Swiss system the ranking 8.5 is assigned to all elements of set 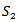 after 4 rounds as this set contains 6 elements which should receive the rankings 6, 7, 8, 9, 10 and 11. As no secondary ranking within the set is taken into account here, all elements get the mean ranking 8.5.
after 4 rounds as this set contains 6 elements which should receive the rankings 6, 7, 8, 9, 10 and 11. As no secondary ranking within the set is taken into account here, all elements get the mean ranking 8.5.Table 3. Cardinality of
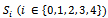 (after several rounds with the Swiss system (after several rounds with the Swiss system
 |
| |
|
Table 4. Awarded ranking for elements of
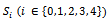 at the end of the tournament at the end of the tournament
 |
| |
|
4. Numerical Results
4.1. Elimination Method
We discuss an example with 16 players in detail where a random generator determines the initial pairing:(9, 8) (13, 5) (10, 1) (4, 16) (2, 3) (14, 6) (11, 12) (7, 15).Applying the elimination method to this initial situation leads to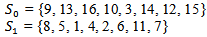 After randomization in
After randomization in 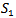 the following pairing is proposed:(5, 6), (4, 2), (11, 8), (1, 7) After two rounds, the players are partitioned into the sets
the following pairing is proposed:(5, 6), (4, 2), (11, 8), (1, 7) After two rounds, the players are partitioned into the sets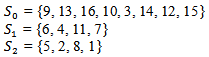 After randomization the following pairing is proposed: (2, 8) (1, 5) After three rounds, the players are partitioned into the sets
After randomization the following pairing is proposed: (2, 8) (1, 5) After three rounds, the players are partitioned into the sets A final fourth round will indicate player 1 as the winner. Remark that with the elimination method the major objective is indicating the winner. The ranking of the other participants is of minor importance. As no supplementary effort is made to determine this complete ranking, there is a gain of number of duels, which is paid by an imprecise ranking of the participants other than the winner. In the example above, player 3 for example ends up in the set of lowest level players. No distinction can be made between him and player 16 and others.
A final fourth round will indicate player 1 as the winner. Remark that with the elimination method the major objective is indicating the winner. The ranking of the other participants is of minor importance. As no supplementary effort is made to determine this complete ranking, there is a gain of number of duels, which is paid by an imprecise ranking of the participants other than the winner. In the example above, player 3 for example ends up in the set of lowest level players. No distinction can be made between him and player 16 and others.
4.2. Swiss System
We start by pairing the 16 players at random as in the previous section with the elimination method. The first round with the Swiss system gives the same sets 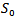 and
and 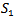 as in the previous section. After randomization in the two sets the following pairing is proposed:(3, 9) (10, 15) (14, 16) (12, 13) (5, 6) (4, 2) (11, 8) (1, 7). Remark that the pairing is made internally within the sets
as in the previous section. After randomization in the two sets the following pairing is proposed:(3, 9) (10, 15) (14, 16) (12, 13) (5, 6) (4, 2) (11, 8) (1, 7). Remark that the pairing is made internally within the sets 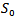 and
and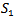 , in order to meet the principle to make duels of players of comparative level. After two rounds, the players are partitioned into the sets
, in order to meet the principle to make duels of players of comparative level. After two rounds, the players are partitioned into the sets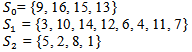 After randomization the following pairing is proposed:(13, 9) (16, 15) (14, 11) (7, 3) (4, 10) (6, 12) (2, 8) (1, 5). After two rounds, the players are partitioned into the sets
After randomization the following pairing is proposed:(13, 9) (16, 15) (14, 11) (7, 3) (4, 10) (6, 12) (2, 8) (1, 5). After two rounds, the players are partitioned into the sets After a last randomization of the sets, the last round with pairs (13, 16) (7, 9) (15, 14) (10, 12) (3, 6) (11, 4) (8, 5) (1, 2) will determine the final ranking given in Table 5.
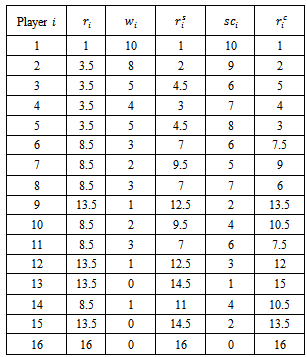
After a last randomization of the sets, the last round with pairs (13, 16) (7, 9) (15, 14) (10, 12) (3, 6) (11, 4) (8, 5) (1, 2) will determine the final ranking given in Table 5. Table 5. Ranking of the different players with the Swiss system (basic and refined version with Solkoff and cumulative tie break methods)
 |
| |
|
This table also mentions the refined ranking 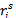 and
and 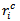 heading tie breaks within the sets
heading tie breaks within the sets 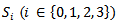 with respectively the Solkoff and the cumulative tie break methods. The final ranking with both the Solkoff and the cumulative method is not perfectly correct. For example in case of the cumulative method, player 3 receives ranking 5 and player 5 receives 3. They both lost one duel, but at different moments (for player 3 is was in an earlier round than for player 5). In case of the Solkoff method their ranking is equal as their opponents were of the same level.In order to evaluate the different tournament classification systems, we need to measure the error of the created ranking. Therefore we consider the error
with respectively the Solkoff and the cumulative tie break methods. The final ranking with both the Solkoff and the cumulative method is not perfectly correct. For example in case of the cumulative method, player 3 receives ranking 5 and player 5 receives 3. They both lost one duel, but at different moments (for player 3 is was in an earlier round than for player 5). In case of the Solkoff method their ranking is equal as their opponents were of the same level.In order to evaluate the different tournament classification systems, we need to measure the error of the created ranking. Therefore we consider the error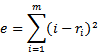 where
where 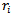 is the ranking for player
is the ranking for player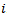 .When no secondary ranking is applied within the sets, the error e takes the value 77.5 for the Swiss system. It can be reduced to
.When no secondary ranking is applied within the sets, the error e takes the value 77.5 for the Swiss system. It can be reduced to 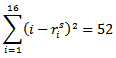 for the Solkoff method and to
for the Solkoff method and to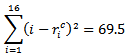 for the cumulative method. As this is just one sample, a better comparison of the methods will arise with a repetition of such a sample. Therefore the Monte Carlo simulation method is appropriate for our analysis.
for the cumulative method. As this is just one sample, a better comparison of the methods will arise with a repetition of such a sample. Therefore the Monte Carlo simulation method is appropriate for our analysis.
4.3. Monte Carlo Simulation of a Chess Tournament
The Monte Carlo simulation[4],[1] technique uses multiple trial runs to discover statistical characteristic features. We apply this method to the tournament case and make several runs of a tournament starting from a random pairing of the players.We consider an error 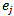 associated with run
associated with run 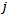 defined as
defined as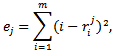 where
where 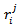 is the ranking for player
is the ranking for player 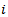 in run number
in run number 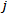 of the simulation. It represents the summed square of the deviation of the expected ranking and the obtained value by each simulation run of the tournament with
of the simulation. It represents the summed square of the deviation of the expected ranking and the obtained value by each simulation run of the tournament with 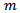 players. The mean value
players. The mean value 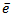 after
after 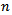 runs can be obtained by
runs can be obtained by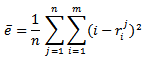 and represents a global error of a ranking method. Figure 1 illustrates the error associated with the elimination method as ranking method. Horizontally the number of the player can be found. Vertically the mean ranking
and represents a global error of a ranking method. Figure 1 illustrates the error associated with the elimination method as ranking method. Horizontally the number of the player can be found. Vertically the mean ranking 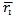 of a player
of a player 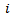 after
after 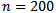 runs in the simulation of the tournament, can be found, where
runs in the simulation of the tournament, can be found, where 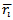 is defined as
is defined as 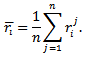
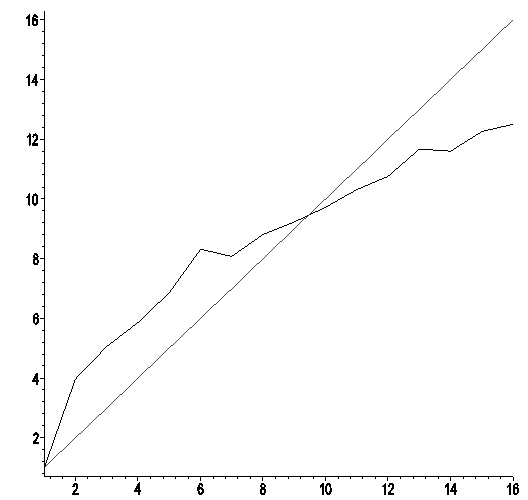 | Figure 1. The mean score after 200 runs with the elimination method versus expected value for the different players |
The expected value is added by the straight line, as we made the assumption that the smaller the number of the player, the better the player. Figure 2 shows the same variables but here the ranking is made with the Swiss system. 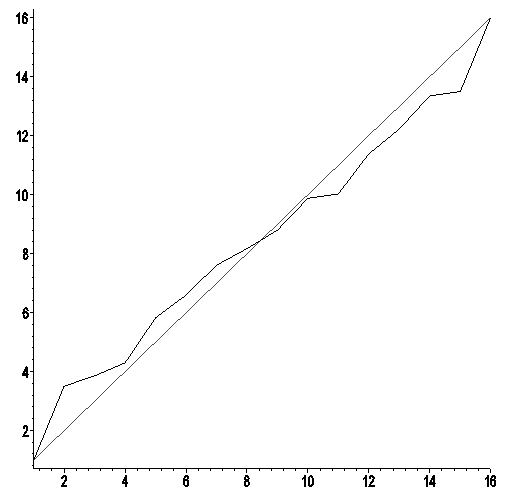 | Figure 2. The mean score after 200 runs with the Swiss system versus expected value for the different players |
Visually it is already clear that the approximation of the first angle bisector is better in case of the Swiss method compared to the elimination method. This is confirmed by the numbers for the mean error 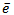 . Further statistics of e including its 95% confidence interval can be compared by means of Table 6.
. Further statistics of e including its 95% confidence interval can be compared by means of Table 6. Table 6. Statistics of the error e
 |
| |
|
5. Conclusions
We were able to develop an error function associated with the Monte-Carlo simulation of tournament classification systems. This quantification revealed the superior classification feature of the Swiss system compared to the elimination system when ranking players at a chess tournament. The Swiss method requires the same number of rounds, but a larger number of duels. A ranking which perfectly represents the quality of the players is the Round Robin, but it has the disadvantage that it requires 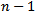 rounds when
rounds when 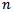 players are involved, which is not practicable. A more refined method with secondary ranking such as the Solkoff and cumulative method were compared in favor of the Solkoff method. Considering the strength of the opponents makes it possible to improve the ranking of the players.
players are involved, which is not practicable. A more refined method with secondary ranking such as the Solkoff and cumulative method were compared in favor of the Solkoff method. Considering the strength of the opponents makes it possible to improve the ranking of the players.
References
| [1] | C.P. Robert, G. Casella, Monte Carlo Statistical Methods, 2nd ed., New York: Springer, 2010. |
| [2] | T. Just, D. Burg, Chess Federation's Official Rules of Chess, McKay, 2003. |
| [3] | www.winbeam.com/~chess/tiebreaks.html |
| [4] | N. Metropolis, S. Ulam, “The Monte Carlo method”, Journal of Amer. Stat. Assoc., Vol. 44, pp.335—341, 1949. |
| [5] | A.W. Root, J.D. McNeil, “Children and chess: a guide for educators”, London: Teacher Ideas Press, pp. 27—28, 2006. |
| [6] | J. Laslier, Tournament Solutions and Majority Voting, Springer-Verlag, Berlin, 1997. |
| [7] | A. Rubinstein, “Ranking the Participants in a Tournament,” SIAM Journal on Applied Mathematics, Vol. 38, 108–111, 1980. |
| [8] | G. Slutzki, O. Volij, “Ranking Participants in Generalized Tournaments”, International Journal of Game Theory, Vol. 33, 255–270, 2005. |
| [9] | M. Brozos-Vazquez, M.A. Campo-Cabana, J.C. Dıaz-Ramos, J. Gonzalez-Dıaz, “Ranking Participants in Tournaments by means of Rating Functions”, Journal of Mathematical Economics, Vol. 44, 1246—1256, 2008. |

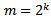 , it is possible to select pairs of players who both won the same number of games, which makes this case the most preferable. We assume one may not play the same player twice within the same tournament.
, it is possible to select pairs of players who both won the same number of games, which makes this case the most preferable. We assume one may not play the same player twice within the same tournament. 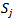 of players who won the same number
of players who won the same number 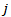 of games, a refinement of the Swiss system is required. Two important tie break methods are the Solkoff method and the cumulative method[3]. The Solkoff method is based on the strength of opponents a player has beaten and is quantified by a weight quantity
of games, a refinement of the Swiss system is required. Two important tie break methods are the Solkoff method and the cumulative method[3]. The Solkoff method is based on the strength of opponents a player has beaten and is quantified by a weight quantity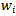 . This weight quantity
. This weight quantity 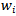 of player
of player 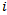 can be defined as the sum of the number of games won by the players beaten by player
can be defined as the sum of the number of games won by the players beaten by player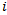 . Within a set
. Within a set 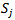 players with higher weights get smaller ranking numbers. For those players with equal weights, the mean of the concerned weight is attributed to each of them. For example: when the ranking numbers 10 and 11 are to be attributed to two players within the same set with equal weights, they are both ranked by number 10.5. The cumulative method is based on the sum
players with higher weights get smaller ranking numbers. For those players with equal weights, the mean of the concerned weight is attributed to each of them. For example: when the ranking numbers 10 and 11 are to be attributed to two players within the same set with equal weights, they are both ranked by number 10.5. The cumulative method is based on the sum 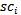 of the cumulative (running) scores for each round of player
of the cumulative (running) scores for each round of player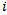 . So if player
. So if player 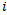 won his first 3 games, lost the fourth game, and won the fifth, his cumulative score is: 1 2 3 3 4. This makes
won his first 3 games, lost the fourth game, and won the fifth, his cumulative score is: 1 2 3 3 4. This makes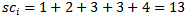 , which would be his cumulative tiebreak. If player
, which would be his cumulative tiebreak. If player 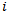 lost his first game, and won the last four, he would have a cumulative tiebreak as follows:
lost his first game, and won the last four, he would have a cumulative tiebreak as follows: 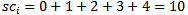 , tiebreak points. The reasoning behind this method is based on the Swiss system of playing an opponent with the same score as oneself. The assumption is that if you win early, you're playing tougher opponents (opponents who also won early and probably finished higher). If you lost in the early rounds, you played weaker opponents (who also lost early and probably didn't finish as high). The higher
, tiebreak points. The reasoning behind this method is based on the Swiss system of playing an opponent with the same score as oneself. The assumption is that if you win early, you're playing tougher opponents (opponents who also won early and probably finished higher). If you lost in the early rounds, you played weaker opponents (who also lost early and probably didn't finish as high). The higher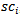 , the better player
, the better player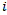 .
.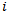 and player
and player 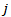 are confronted, player
are confronted, player 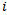 will win if
will win if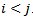 . As the goal of a tournament is to create a classification of players that represents their level, we expect as outcome of the tournament: player
. As the goal of a tournament is to create a classification of players that represents their level, we expect as outcome of the tournament: player 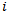 ends up at ranking
ends up at ranking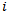 .
.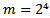 , a winner can be indicated after four rounds.
, a winner can be indicated after four rounds.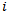 rounds,
rounds, 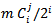 players were able to win
players were able to win 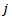 games with the Swiss system, as is shown in Table 3 where the cardinality of the sets
games with the Swiss system, as is shown in Table 3 where the cardinality of the sets 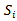 is given at the different stages of the tournament. Here
is given at the different stages of the tournament. Here 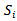 is the set of players who have won
is the set of players who have won 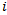 games so far.Table 2 gives analogous cardinalities with the elimination system.
games so far.Table 2 gives analogous cardinalities with the elimination system.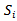 . They all receive the same mean ranking of the set they are in (see Table 4 based on the cardinalities of Table 2 and 3 to determine the mean values). For example, for the Swiss system the ranking 8.5 is assigned to all elements of set
. They all receive the same mean ranking of the set they are in (see Table 4 based on the cardinalities of Table 2 and 3 to determine the mean values). For example, for the Swiss system the ranking 8.5 is assigned to all elements of set 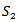 after 4 rounds as this set contains 6 elements which should receive the rankings 6, 7, 8, 9, 10 and 11. As no secondary ranking within the set is taken into account here, all elements get the mean ranking 8.5.
after 4 rounds as this set contains 6 elements which should receive the rankings 6, 7, 8, 9, 10 and 11. As no secondary ranking within the set is taken into account here, all elements get the mean ranking 8.5.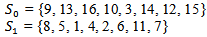 After randomization in
After randomization in 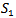 the following pairing is proposed:(5, 6), (4, 2), (11, 8), (1, 7) After two rounds, the players are partitioned into the sets
the following pairing is proposed:(5, 6), (4, 2), (11, 8), (1, 7) After two rounds, the players are partitioned into the sets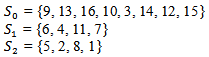 After randomization the following pairing is proposed: (2, 8) (1, 5) After three rounds, the players are partitioned into the sets
After randomization the following pairing is proposed: (2, 8) (1, 5) After three rounds, the players are partitioned into the sets A final fourth round will indicate player 1 as the winner. Remark that with the elimination method the major objective is indicating the winner. The ranking of the other participants is of minor importance. As no supplementary effort is made to determine this complete ranking, there is a gain of number of duels, which is paid by an imprecise ranking of the participants other than the winner. In the example above, player 3 for example ends up in the set of lowest level players. No distinction can be made between him and player 16 and others.
A final fourth round will indicate player 1 as the winner. Remark that with the elimination method the major objective is indicating the winner. The ranking of the other participants is of minor importance. As no supplementary effort is made to determine this complete ranking, there is a gain of number of duels, which is paid by an imprecise ranking of the participants other than the winner. In the example above, player 3 for example ends up in the set of lowest level players. No distinction can be made between him and player 16 and others.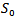 and
and 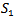 as in the previous section. After randomization in the two sets the following pairing is proposed:(3, 9) (10, 15) (14, 16) (12, 13) (5, 6) (4, 2) (11, 8) (1, 7). Remark that the pairing is made internally within the sets
as in the previous section. After randomization in the two sets the following pairing is proposed:(3, 9) (10, 15) (14, 16) (12, 13) (5, 6) (4, 2) (11, 8) (1, 7). Remark that the pairing is made internally within the sets 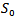 and
and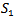 , in order to meet the principle to make duels of players of comparative level. After two rounds, the players are partitioned into the sets
, in order to meet the principle to make duels of players of comparative level. After two rounds, the players are partitioned into the sets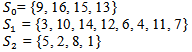 After randomization the following pairing is proposed:(13, 9) (16, 15) (14, 11) (7, 3) (4, 10) (6, 12) (2, 8) (1, 5). After two rounds, the players are partitioned into the sets
After randomization the following pairing is proposed:(13, 9) (16, 15) (14, 11) (7, 3) (4, 10) (6, 12) (2, 8) (1, 5). After two rounds, the players are partitioned into the sets After a last randomization of the sets, the last round with pairs (13, 16) (7, 9) (15, 14) (10, 12) (3, 6) (11, 4) (8, 5) (1, 2) will determine the final ranking given in Table 5.
After a last randomization of the sets, the last round with pairs (13, 16) (7, 9) (15, 14) (10, 12) (3, 6) (11, 4) (8, 5) (1, 2) will determine the final ranking given in Table 5. 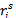 and
and 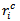 heading tie breaks within the sets
heading tie breaks within the sets 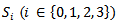 with respectively the Solkoff and the cumulative tie break methods. The final ranking with both the Solkoff and the cumulative method is not perfectly correct. For example in case of the cumulative method, player 3 receives ranking 5 and player 5 receives 3. They both lost one duel, but at different moments (for player 3 is was in an earlier round than for player 5). In case of the Solkoff method their ranking is equal as their opponents were of the same level.In order to evaluate the different tournament classification systems, we need to measure the error of the created ranking. Therefore we consider the error
with respectively the Solkoff and the cumulative tie break methods. The final ranking with both the Solkoff and the cumulative method is not perfectly correct. For example in case of the cumulative method, player 3 receives ranking 5 and player 5 receives 3. They both lost one duel, but at different moments (for player 3 is was in an earlier round than for player 5). In case of the Solkoff method their ranking is equal as their opponents were of the same level.In order to evaluate the different tournament classification systems, we need to measure the error of the created ranking. Therefore we consider the error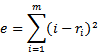 where
where 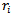 is the ranking for player
is the ranking for player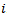 .When no secondary ranking is applied within the sets, the error e takes the value 77.5 for the Swiss system. It can be reduced to
.When no secondary ranking is applied within the sets, the error e takes the value 77.5 for the Swiss system. It can be reduced to 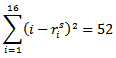 for the Solkoff method and to
for the Solkoff method and to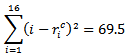 for the cumulative method. As this is just one sample, a better comparison of the methods will arise with a repetition of such a sample. Therefore the Monte Carlo simulation method is appropriate for our analysis.
for the cumulative method. As this is just one sample, a better comparison of the methods will arise with a repetition of such a sample. Therefore the Monte Carlo simulation method is appropriate for our analysis.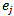 associated with run
associated with run 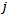 defined as
defined as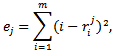 where
where 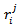 is the ranking for player
is the ranking for player 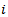 in run number
in run number 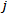 of the simulation. It represents the summed square of the deviation of the expected ranking and the obtained value by each simulation run of the tournament with
of the simulation. It represents the summed square of the deviation of the expected ranking and the obtained value by each simulation run of the tournament with 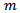 players. The mean value
players. The mean value 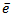 after
after 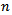 runs can be obtained by
runs can be obtained by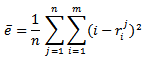 and represents a global error of a ranking method. Figure 1 illustrates the error associated with the elimination method as ranking method. Horizontally the number of the player can be found. Vertically the mean ranking
and represents a global error of a ranking method. Figure 1 illustrates the error associated with the elimination method as ranking method. Horizontally the number of the player can be found. Vertically the mean ranking 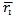 of a player
of a player 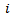 after
after 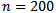 runs in the simulation of the tournament, can be found, where
runs in the simulation of the tournament, can be found, where 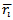 is defined as
is defined as 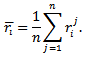


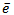 . Further statistics of e including its 95% confidence interval can be compared by means of Table 6.
. Further statistics of e including its 95% confidence interval can be compared by means of Table 6. 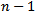 rounds when
rounds when 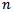 players are involved, which is not practicable. A more refined method with secondary ranking such as the Solkoff and cumulative method were compared in favor of the Solkoff method. Considering the strength of the opponents makes it possible to improve the ranking of the players.
players are involved, which is not practicable. A more refined method with secondary ranking such as the Solkoff and cumulative method were compared in favor of the Solkoff method. Considering the strength of the opponents makes it possible to improve the ranking of the players. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
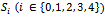 after several rounds with the elimination system
after several rounds with the elimination system
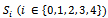 (after several rounds with the Swiss system
(after several rounds with the Swiss system
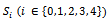 at the end of the tournament
at the end of the tournament

