Habib Jafari, Shima Pirmohamadi, Sedighe Parviz
Department of Statistics, Razi University, Kermanshsh, Iran
Correspondence to: Habib Jafari, Department of Statistics, Razi University, Kermanshsh, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
During sampling, a researcher may sometimes encounter a population, in which selection chance of each one of the samples is not equal; in such a situation, it is better to utilize weighted distribution instead of main distribution for data analysis. Accordingly, considering a weighted distribution (for a state in which response variable has such a distribution in a linear regression model) and also a multiple regression (two regressors) model, this paper proposed an appropriate design (for estimating the parameters) using the known optimality design (D-optimality) to obtain optimality of the presented design.
Keywords:
Optimal Criterion, Optimal Design, D-Optimal Design, Weighted Distribution
Cite this paper: Habib Jafari, Shima Pirmohamadi, Sedighe Parviz, On Optimal Design for Regression Model (with Two Independent Variables) Considering Weighted Normal Distribution, Applied Mathematics, Vol. 3 No. 4, 2013, pp. 125-127. doi: 10.5923/j.am.20130304.02.
1. Introduction
Assume that, while sampling from a population, chance of selecting the samples is not equal. In such a case, samples would follow a weighted distribution. Weighted distributions which are obtained from a main distribution could have various weights; selection of weights depends on sample types and sampling conditions[6]. The weight which is used here has been known as a skewed length and occurs when the selection possibility of a distance is in proportion to length of that distance[7]. In this study, a linear regression model with two independent variables was considered so that its response variable had normal weighted distribution with the mentioned weight. In this state, to estimate available parameters in the presented model, a suitable design was introduced and a desirable optimality criterion (Section 4) was used to locally optimize the introduced design (in this article, non-linear models were considered and local optimization method was used considering the application of the presented criterion and dependence of Fisher information matrix on the parameters). Accordingly, the article structure is as follows:In Section 2, linear regression model and weighted distribution for its response variable are presented. Fisher information matrix in normal weighted distribution is presented in Section 3. Locally D-optimal design for some of the partitioned spaces of parameters is given in Section 4 and Section 5 concludes the paper.
2. Linear Regression Model with Skewed Responses
Assume 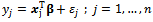 , in which
, in which 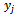 is a response variable,
is a response variable, 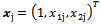 is vector of regression function,
is vector of regression function, 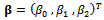 is vector of unknown parameters,
is vector of unknown parameters, 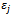 is random error and
is random error and 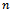 is sample volume. In the above presented regression model, response variable has normal distribution as
is sample volume. In the above presented regression model, response variable has normal distribution as 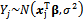 . Now, without losing generality, assume
. Now, without losing generality, assume 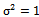 ; thus, density function of
; thus, density function of 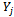 random variable will be as:
random variable will be as: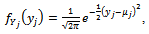 | (1) |
in which 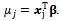 .Density function of weighted distribution is generally defined as[5]:
.Density function of weighted distribution is generally defined as[5]: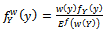 | (2) |
where 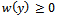 and is called weight function so that
and is called weight function so that 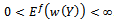 .Accordingly,
.Accordingly, 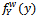 has the conditions of density function.As mentioned in Section 1, the weight which was studied here was weight of skewed length; i.e.
has the conditions of density function.As mentioned in Section 1, the weight which was studied here was weight of skewed length; i.e. 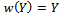 ; however, since
; however, since 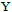 has normal distribution, positive condition of
has normal distribution, positive condition of 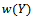 will not always hold. Therefore, the truncate distribution of Y in
will not always hold. Therefore, the truncate distribution of Y in 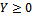 is used, in which case density function of normal weighted distribution is as follows:
is used, in which case density function of normal weighted distribution is as follows: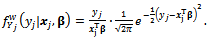 | (3) |
In this relation, mean is regarded greater than 4[4] .According to what was mentioned in the introduction, a suitable design was considered in the following way in order to estimate passive parameters: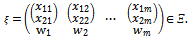 | (4) |
Then, the present design was optimized using D–optimality criterion (Section1-4). In Relation (4), 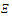 is space design which is defined as
is space design which is defined as 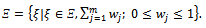 Considering definition of the criterion used in this study, Fisher information matrix should be calculated for each and every member of Design (4). Then, the information matrix related to the mentioned design will be calculated as:
Considering definition of the criterion used in this study, Fisher information matrix should be calculated for each and every member of Design (4). Then, the information matrix related to the mentioned design will be calculated as: 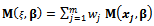 | (5) |
where 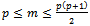 and
and 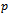 is the number of unknown parameters[8].
is the number of unknown parameters[8].
3. Fisher Information Matrix
Fisher information matrix for each and every observation (related to Design (4)) in a non-weighted distribution is as follows: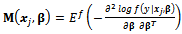 | (6) |
And in a weight distribution, it refers to:[5]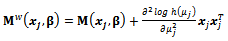 | (7) |
where 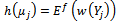 . Now, calculating
. Now, calculating 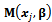 ,
,  and Equation (7), the following can be given:
and Equation (7), the following can be given: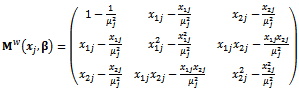 This matrix depends on unknown parameters and will be used in the following section to obtain the optimal design.
This matrix depends on unknown parameters and will be used in the following section to obtain the optimal design.
4. Locally D-optimal Design
Information matrix is very important in optimal designs since various types of optimality criteria are defined based on the information matrix. Among optimality criteria, D- criterion is used and focused more frequently due to its stability and that is why this criterion was also used in this study. In general terms, D-optimality criterion is defined as 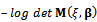 [1]. Since information matrix of weighted distribution is considered here, the aforesaid criterion will be defined as
[1]. Since information matrix of weighted distribution is considered here, the aforesaid criterion will be defined as 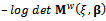 .To calculate an optimal design, first, a design with the determined number of points should be considered[3]. Three, four, five and six point designs could be assumed based on the number of model's unknown parameters according to Carathéodory’s theorem[8]. The designs considered here included three and four point designs.As mentioned in Section 3,
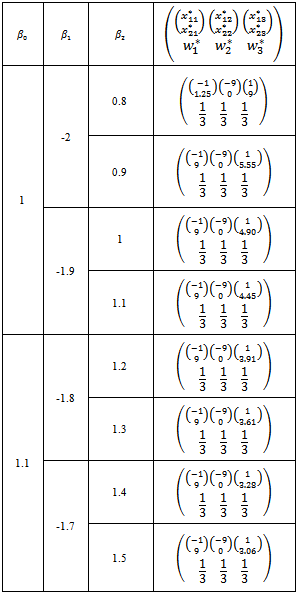
.To calculate an optimal design, first, a design with the determined number of points should be considered[3]. Three, four, five and six point designs could be assumed based on the number of model's unknown parameters according to Carathéodory’s theorem[8]. The designs considered here included three and four point designs.As mentioned in Section 3, 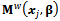 depends on unknown parameters; therefore, D-optimal design was locally calculated in this study.In Table 1, locally D-optimal design is calculated in terms of various values of parameters when the number of points in this design is equal to the number of parameters. Table 2 shows locally D-optimal design for a state in which the number of points is four.In Tables 1 and 2,
depends on unknown parameters; therefore, D-optimal design was locally calculated in this study.In Table 1, locally D-optimal design is calculated in terms of various values of parameters when the number of points in this design is equal to the number of parameters. Table 2 shows locally D-optimal design for a state in which the number of points is four.In Tables 1 and 2, 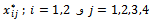 and
and 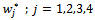 are respectively points and weights of D-optimal design. Additionally,
are respectively points and weights of D-optimal design. Additionally, 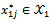 ,
, 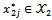 ,
, 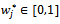 and
and 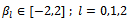 in which
in which 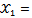
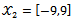 .It is noteworthy that values of weights in these tables are rounded up to three decimal places.
.It is noteworthy that values of weights in these tables are rounded up to three decimal places.Table 1. Locally D-optimal design with three points
 |
| |
|
Table 1 shows that, if the number of points in the design is equal to the number of unknown parameters, in this case, the uniform design would be optimal[8]; however, points of the design would change considering the values for the unknown parameters.Table 2. Locally D-optimal design with four points
 |
| |
|
5. Conclusions
If selection chance of sampling is not equal, a weighted distribution is considered for analyzing the data. In this study, this weighted distribution was studied for the response variable in a multiple linear regression model (with two regressors). The focused weighted distribution was a normal weighted distribution with the weight function of skewed length. In order to obtain D-optimal design, first, Fisher information matrix was calculated based on the weighted distribution so that the information matrix related to the weighted distribution was obtained in terms of information matrix of the main distribution. Then, D-optimal design was locally calculated considering the dependence of information matrix on the model's unknown parameters. Locally D-optimal designs are mentioned in Tables 1 and 2 as specific states of D-optimal designs for some values of parameters.In addition to three and four point designs, five and six point designs could be considered and locally D-optimal designs can be also calculated in such states.
ACKNOWLEDGEMENTS
This work is partially supported by the Cooperative 4407 knowledge Base New Ideas.
References
| [1] | Atkinson, A.C., Donev, A.N., Tobias, R.D. (2006). Optimum Experimental Designs, with SAS. Oxford University Press. |
| [2] | Dette, H., Melas, V.B., Wong, W.K. (2005). Optimal Design for Goodness-of-Fit of the Michaelis-Menten Enzyme Kinetic Function. J. Am. Stat. Assoc 100:1370-1381. |
| [3] | Ford, I., Torsney, B., Wu, G.F.J. (1992). The Use of a Canonical Form in the construction of Locally Optimal Designs for non-Linear Problems. J R Stat Soc Ser B 54:569-583. |
| [4] | Navarro, J., Ruiz, J.M., del Aguila, Y. (2001). Parametric Estimation from Weighted Samples. Biom J 43:297-311. |
| [5] | Ortiz, I., Martinez, I., Rodriguez, C., del Aguila, Y. (2009). Optimal Designs for Generalized Linear Models with Biased Response. Metrika 70:225-237. |
| [6] | Patil, G.P., Rao, C.R., (1978). Weighted Distribution and Size-Biased with Applications to Wildlife Populations and Human Families. Biometrics 34:179-189. |
| [7] | Satten, G.A., Kong, F., Wright, Glynn, S., Schreiber, G., (2004). How Special Is a Special Interval:Modeling Departure from Length-Biased Sampling in Renewal Processes. Biostatistics 5:145-151. |
| [8] | Silvey, S.D. (1980). Optimal Design an Introduction to the Theory for parameter Estimation. London:Chapman and Hall. |

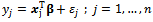 , in which
, in which 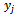 is a response variable,
is a response variable, 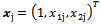 is vector of regression function,
is vector of regression function, 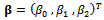 is vector of unknown parameters,
is vector of unknown parameters, 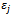 is random error and
is random error and 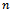 is sample volume. In the above presented regression model, response variable has normal distribution as
is sample volume. In the above presented regression model, response variable has normal distribution as 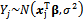 . Now, without losing generality, assume
. Now, without losing generality, assume 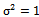 ; thus, density function of
; thus, density function of 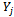 random variable will be as:
random variable will be as: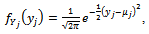
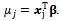 .Density function of weighted distribution is generally defined as[5]:
.Density function of weighted distribution is generally defined as[5]: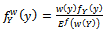
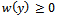 and is called weight function so that
and is called weight function so that 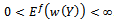 .Accordingly,
.Accordingly, 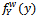 has the conditions of density function.As mentioned in Section 1, the weight which was studied here was weight of skewed length; i.e.
has the conditions of density function.As mentioned in Section 1, the weight which was studied here was weight of skewed length; i.e. 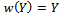 ; however, since
; however, since 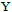 has normal distribution, positive condition of
has normal distribution, positive condition of 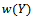 will not always hold. Therefore, the truncate distribution of Y in
will not always hold. Therefore, the truncate distribution of Y in 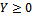 is used, in which case density function of normal weighted distribution is as follows:
is used, in which case density function of normal weighted distribution is as follows: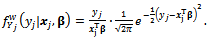
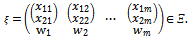
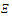 is space design which is defined as
is space design which is defined as 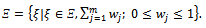 Considering definition of the criterion used in this study, Fisher information matrix should be calculated for each and every member of Design (4). Then, the information matrix related to the mentioned design will be calculated as:
Considering definition of the criterion used in this study, Fisher information matrix should be calculated for each and every member of Design (4). Then, the information matrix related to the mentioned design will be calculated as: 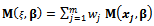
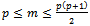 and
and 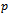 is the number of unknown parameters[8].
is the number of unknown parameters[8].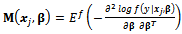
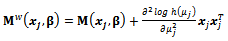
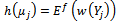 . Now, calculating
. Now, calculating 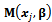 ,
,  and Equation (7), the following can be given:
and Equation (7), the following can be given: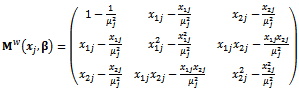 This matrix depends on unknown parameters and will be used in the following section to obtain the optimal design.
This matrix depends on unknown parameters and will be used in the following section to obtain the optimal design.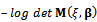 [1]. Since information matrix of weighted distribution is considered here, the aforesaid criterion will be defined as
[1]. Since information matrix of weighted distribution is considered here, the aforesaid criterion will be defined as 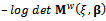 .To calculate an optimal design, first, a design with the determined number of points should be considered[3]. Three, four, five and six point designs could be assumed based on the number of model's unknown parameters according to Carathéodory’s theorem[8]. The designs considered here included three and four point designs.As mentioned in Section 3,
.To calculate an optimal design, first, a design with the determined number of points should be considered[3]. Three, four, five and six point designs could be assumed based on the number of model's unknown parameters according to Carathéodory’s theorem[8]. The designs considered here included three and four point designs.As mentioned in Section 3, 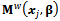 depends on unknown parameters; therefore, D-optimal design was locally calculated in this study.In Table 1, locally D-optimal design is calculated in terms of various values of parameters when the number of points in this design is equal to the number of parameters. Table 2 shows locally D-optimal design for a state in which the number of points is four.In Tables 1 and 2,
depends on unknown parameters; therefore, D-optimal design was locally calculated in this study.In Table 1, locally D-optimal design is calculated in terms of various values of parameters when the number of points in this design is equal to the number of parameters. Table 2 shows locally D-optimal design for a state in which the number of points is four.In Tables 1 and 2, 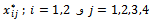 and
and 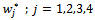 are respectively points and weights of D-optimal design. Additionally,
are respectively points and weights of D-optimal design. Additionally, 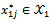 ,
, 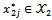 ,
, 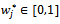 and
and 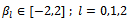 in which
in which 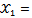
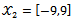 .It is noteworthy that values of weights in these tables are rounded up to three decimal places.
.It is noteworthy that values of weights in these tables are rounded up to three decimal places. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
