-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2013; 3(3): 107-115
doi:10.5923/j.am.20130303.04
Free Convection Flow of Fluid with Variable Viscosity from a Porous Vertical Plate in Presence of Heat Generation
Amena Ferdousi1, M. Mostafizur Rahman2, Mohammad Salek Parvez3, M. A. Alim4
1Faculty of Electronics and Electrical Engineering, Eastern University, Dhaka, Bangladesh
2Department of Computer Science and Engineering, Daffodil International University, Dhaka, Bangladesh
3Department of Natural Sciences, Daffodil International University, Dhaka, Bangladesh
4Department of Mathematics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
Correspondence to: Amena Ferdousi, Faculty of Electronics and Electrical Engineering, Eastern University, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents a new extension for free convection flow with variable viscosity from a porous vertical plate in presence of heat generation. The governing boundary layer equations are first transformed into a non dimensional form and the resulting non linear system of partial differential equations are then solved numerically using finite difference method together with Keller-Box scheme. The numerical results show that the variable viscosity affects the surface shear stress and the rate of heat transfer, which are here in terms of skin friction coefficient and local Nusselt number. It affects velocity as well as temperature profiles also. These are shown graphically and tabular form for a selection of parameters set of consisting of viscosity variation parameter γ, heat generation parameter Q, Prandtl number Pr.
Keywords: Porous Plate, Heat Generation, Natural Convection, Variable Viscosity
Cite this paper: Amena Ferdousi, M. Mostafizur Rahman, Mohammad Salek Parvez, M. A. Alim, Free Convection Flow of Fluid with Variable Viscosity from a Porous Vertical Plate in Presence of Heat Generation, Applied Mathematics, Vol. 3 No. 3, 2013, pp. 107-115. doi: 10.5923/j.am.20130303.04.
Article Outline
1. Introduction
- The study of heat generation or absorption in moving fluids is important in problems dealing with chemical reactions and those concerned with dissociating fluids. Possible heat generation effects may alter the temperature distribution; consequently the particle deposition rate in nuclear reactors, electronic chips and semiconductor wafers.Free convection flow with variable viscosity from porous vertical plate in presence of heat generation has been drawn forth not only for its fundamental aspects but also for its significance in the contexts of space technology and processes involving high temperature. In the presence of heat generation, variable viscosity free convection boundary layer flow from a porous vertical plate of a steady two dimensional viscous incompressible fluid and the radiated heat transfer has been investigated. In this analysis consideration had been given to grey gases that emit and absorb but do not scatter thermal radiation. Over the work it is assumed that the surface temperature of the porous vertical plate, Tw, is constant, where Tw>T∞. Here T∞ is the ambient temperature of the fluid, T is the temperature of the fluid in the boundary layer, g is the acceleration due to gravity, the fluid is assumed to be a grey emitting and absorbing, but non scattering medium. Merkin[1] concluded free convection with blowing and suction. Lin and Yu[2] studied free convection on a horizontal plate with blowing and suction. Hossain et al[3] studied the effect of radiation on free convection flow with variable viscosity from a porous vertical plate. Hossain et al.[4] performed flow of viscous incompressible fluid with temperature dependent viscosity and thermal conductivity past a permeable wedge with variable heat flux. Hossain and Takhar[5] studied radiation effect on mixed convection along a vertical plate with uniform surface temperature. Molla et al.[6] studied natural convection flow along a vertical wavy surface with uniform surface temperature in presence of heat generation/absorption. Akhter[7] studied the effect of radiations on free convection flow on sphere with isothermal surface and uniform heat flux. Ali[8] studied the effect of radiation on free convection flow on sphere with heat generation. Hossain et al.[9] studied the effect of radiation on free convection flow from a porous vertical plate. They[9] analyzed a full numerical solution and found an increase in Radiation parameter Rd causes to thin the boundary layer and an increase in surface temperature parameter causes to thicken the boundary layer. The presence of suction ensures that its ultimate fate if vertically increased is a layer of constant thickness. Vajravelu and Hadjinicolaou[10] perfomed the heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation In this study, they considered that the volumetric rate of heat generation,
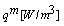 should be
should be 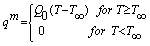 where
where 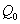 is the heat generation constant. The above relation explained is valid as an approximation of the state of some exothermic process and having
is the heat generation constant. The above relation explained is valid as an approximation of the state of some exothermic process and having 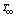 as the onset temperature. When the inlet temperature is not less than
as the onset temperature. When the inlet temperature is not less than 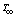 they used
they used 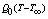 . Molla et al.[11] studied the Magnetohydrodynamic natural convection flow on a sphere with uniform heat flux in presence of heat generation. The physical property, variable viscosity may change significantly with temperature. Accordingly, Gary et al.[12] and Mehta and Sood[13] have concluded that when this effect is included, the flow characteristics substantially change compared to the constant viscosity case. Recently, Kafoussius and Williams[14] and Kafoussias and Rees[15] have investigated the effect of the temperature-dependent viscosity on the mixed convection flow past a vertical flat plate in the region near the leading edge using the local non-similarity method. In these studies, they concluded that when the viscosity of a fluid is sensitive to temperature variations, the effect of temperature-dependent viscosity has to be taken into consideration, otherwise considerable errors may occur in the characteristics of the heat transfer process. Hossain and Kabir[16] have investigated the natural convection flow from a vertical wavy surface. Hossain and Munir[17] investigated the mixed convection flow from a vertical flat plate for a temperature dependent viscosity. In the studies[16][17] the viscosity of the fluid has been Carey and Mollendorf[18] studied natural convection in liquid with temperature dependent viscosity. considered to be inversely proportional to a linear function of temperature. In all the above studies were confined without any heat generation None of the aforementioned studies, considered variable viscosity and the heat generation effects on laminar boundary layer flow of the fluids along porous plate. In the present study, we have investigated free convection flow with variable viscosity from a porous vertical plate in presence heat generation numerically. The results will be obtained for different values of relevant physical parameters and will be shown in graphs as well as in tables.The governing partial differential equations are reduced to locally non-similar partial differential forms by adopting some appropriate transformations. The transformed boundary layer equations are solved numerically using implicit finite difference scheme together with the Keller box technique[19] . Here, we have focused our attention on the evolution of the surface shear stress in terms of local skin friction and the rate of heat transfer in terms of local Nusselt number, velocity profiles as well as temperature profiles for selected values of parameters consisting of heat generation parameter Q, variable viscosity γ, Prandtl number Pr.
. Molla et al.[11] studied the Magnetohydrodynamic natural convection flow on a sphere with uniform heat flux in presence of heat generation. The physical property, variable viscosity may change significantly with temperature. Accordingly, Gary et al.[12] and Mehta and Sood[13] have concluded that when this effect is included, the flow characteristics substantially change compared to the constant viscosity case. Recently, Kafoussius and Williams[14] and Kafoussias and Rees[15] have investigated the effect of the temperature-dependent viscosity on the mixed convection flow past a vertical flat plate in the region near the leading edge using the local non-similarity method. In these studies, they concluded that when the viscosity of a fluid is sensitive to temperature variations, the effect of temperature-dependent viscosity has to be taken into consideration, otherwise considerable errors may occur in the characteristics of the heat transfer process. Hossain and Kabir[16] have investigated the natural convection flow from a vertical wavy surface. Hossain and Munir[17] investigated the mixed convection flow from a vertical flat plate for a temperature dependent viscosity. In the studies[16][17] the viscosity of the fluid has been Carey and Mollendorf[18] studied natural convection in liquid with temperature dependent viscosity. considered to be inversely proportional to a linear function of temperature. In all the above studies were confined without any heat generation None of the aforementioned studies, considered variable viscosity and the heat generation effects on laminar boundary layer flow of the fluids along porous plate. In the present study, we have investigated free convection flow with variable viscosity from a porous vertical plate in presence heat generation numerically. The results will be obtained for different values of relevant physical parameters and will be shown in graphs as well as in tables.The governing partial differential equations are reduced to locally non-similar partial differential forms by adopting some appropriate transformations. The transformed boundary layer equations are solved numerically using implicit finite difference scheme together with the Keller box technique[19] . Here, we have focused our attention on the evolution of the surface shear stress in terms of local skin friction and the rate of heat transfer in terms of local Nusselt number, velocity profiles as well as temperature profiles for selected values of parameters consisting of heat generation parameter Q, variable viscosity γ, Prandtl number Pr.2. Problem Description and Mathematical Model
- We have investigated the effect of radiation with variable viscosity on free convection flow from a porous plate in presence of heat generation. The fluid is assumed to be a grey, emitting and absorbing but non scattering medium. Over the work it is assumed that the surface temperature of the porous vertical plate, Tw, is constant, where
 . The physical configuration considered is as shown in Fig.1:
. The physical configuration considered is as shown in Fig.1: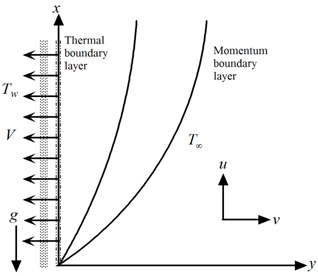 | Figure 1. The coordinate system and the physical model |
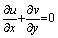 | (1) |
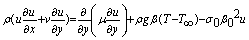 | (2) |
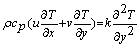 | (3) |
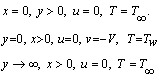 | (4) |
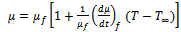 | (5a) |
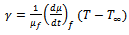 | (5b) |
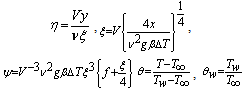 | (6) |
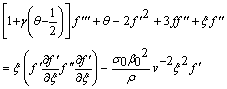 | (7) |
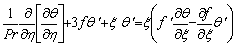 | (8) |
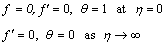 | (9) |
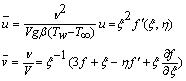 | (10) |
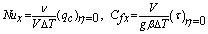 | (11) |
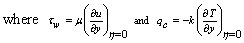 | (12) |
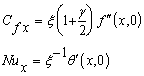 | (13) |
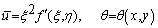 | (14) |
3. Numerical Procedure
- Solution of the local non similar partial differential equation (7) to (8) subjected to the boundary condition (9) are obtained by using implicit finite difference method with Keller-Box Scheme[19], which has been described in details by Cebeci[20].The solution methodology of equations (7) and (8) with the boundary condition given in eqn. (9) for the entire ξ values based on Keller – box scheme is proposed here. The scheme specifically incorporated a nodal distribution favoring the vicinity of the plate, enabling accuracy to be maintained in this region of steep gradient. In detail equations (7) and (8) are solved as a set of five simultaneous equations.
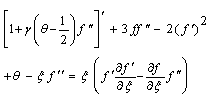 | (15) |
 | (16) |
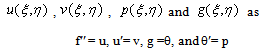 | (17) |
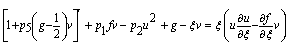 | (18) |
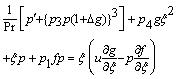 | (19) |
 | (20) |
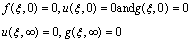 | (21) |
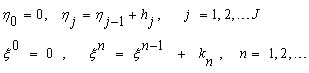 We approximate the quantities (f,u,v,p) at the points
We approximate the quantities (f,u,v,p) at the points 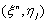 of the net by
of the net by 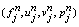 which we call net function.
which we call net function. 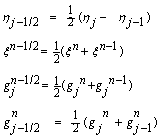 | (22) |
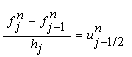 | (23) |
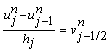 | (24) |
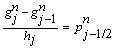 | (25) |
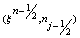 . Centering the Equations (22) about the point
. Centering the Equations (22) about the point 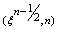 without specifying η to obtain the algebraic equations. The difference approximation to Equations (18)-(19) become
without specifying η to obtain the algebraic equations. The difference approximation to Equations (18)-(19) become  The corresponding boundary conditions (21) become
The corresponding boundary conditions (21) become 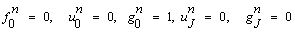 which just express the requirement for the boundary conditions to remain during the iteration process. Now we will convert the momentum and energy equations into system of linear Equations and together with the boundary conditions can be written in matrix or vector form, where the coefficient matrix has a block tri-diagonal structure. The whole procedure, namely reduction to first order followed by central difference approximations, Newton’s quasi - linearization method and the block Thomas algorithm, is well known as the Keller- box method.
which just express the requirement for the boundary conditions to remain during the iteration process. Now we will convert the momentum and energy equations into system of linear Equations and together with the boundary conditions can be written in matrix or vector form, where the coefficient matrix has a block tri-diagonal structure. The whole procedure, namely reduction to first order followed by central difference approximations, Newton’s quasi - linearization method and the block Thomas algorithm, is well known as the Keller- box method. 4. Results and Discussion
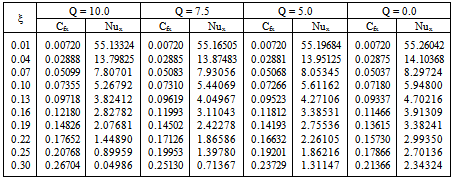
- In this exertion variable viscosity on free convection flow from a porous vertical plate in presence of heat generation is investigated. Numerical values of local rate of heat transfer are calculated in terms of Nusselt number Nux for the surface of the porous vertical plate from lower stagnation point to upper stagnation point, for different values of the aforementioned parameters and these are shown in tabular form in Table 1 and Graphically in Figure 5-7. The effect for different values viscosity γ on local skin friction coefficient Cfx and the local Nusselt number Nux, as well as velocity and temperature profiles are displayed in Fig.2 to 7. The aim of these figures are to display how the profiles vary in , the selected streetwise co-ordinate.Figures 2(a)-2(b) display results for the velocity and temperature profiles, for different values of viscosity parameter γ = -1.0, 0.5, 1.0, 1.5, 1.9 while Prandtl number Pr = 1.0, surface temperature parameter θw = 1.1 and heat generation Q = 1.0. It has been seen from Figures 2(a)-2(b) that as the viscosity parameter γ increases, the velocity profiles decreases and the temperature profiles increase. The velocity is zero at the boundary wall then the velocity increases to the peak value as η increases and from η = 1 toη = 2 it is reverse and after η = 2 it is decreasing, finally the velocity approaches to zero (the asymptotic value). The changes of temperature profiles in the η direction also shows the typical temperature profiles for natural convection boundary layer flow that is the value of temperature profiles is 1.0 (one) at the boundary wall then the temperature profile decreases gradually η direction to the asymptotic value. However, in figures 3(a)-3(b) it has been shown that when the Prandtl number Pr = 0.7, 0.8, 0.9, 1.0 and 1.1 increases with θw = 1.1, Q = 1.0 and γ = 1.0 both the velocity and temperature profiles decrease.Figures 4(a) display results for the velocity profiles for different values of heat generation parameter Q with Prandtl number Pr = 1.0, viscosity parameter γ = 1.0 and surface temperature parameter θw = 1.1. It has been seen from figure 4(a) that as the heat generation parameter increases the velocity profiles increase. It is also observed from figure 4(a) that the changes of velocity profiles in the η direction reveals the typical velocity profile for natural convection boundary layer flow, i.e., the velocity is zero at the boundary wall then the velocity increases to the peak value as η increases and finally the velocity approaches to zero (the asymptotic value). The maximum values of velocity are recorded to be 0.33241, 0.29610, 0.26241, at η = 0.99806 0.22683, 0.21692 at η = 0.94233 for Q =.10.0, 7.5, 5.0, 2.0, and 0.0. The velocity is 0.33241 is the maximum at η = 0.99806 for Q = 10.0. Here, it is observed that at η = 0.99806, the velocity increases by 53.21% as the heat generation parameter Q changes from 0 to 10.0.From figure 4(b), as the heat generation parameter Q increases, the temperature profiles increase. We observed that the temperature profile is 1.0 (one) at the boundary wall then the temperature profile decreases gradually along η direction to the asymptotic value. But for Q = 10.0, 7.5 the temperature profile increases, at η= 0.45434 it is 1.30298, at η = 0.32549 it is 1.08706 then it decrease. And for other values it is gradually decreasing.Figure 5(a) shows that skin friction coefficient Cfx increases for increasing values of viscosity parameter γ with Prandtl number Pr = 1.0, surface temperature parameter θw = 1.1 and heat generation Q =1.0. It is observed from Figure 5(a) that the skin friction increases gradually from zero value at lower stagnation point along the ξ direction and from Figure 5(b); it reveals that the rate of heat transfer decreases along the ξ direction for γ = -1.0, 0.5, 1.0, 1.5 and 1.9 Nux are along ξ axis. A hot fluid layer is created adjacent to the interface of the wall due to the viscosity mechanism and ultimately the resultant temperature of the fluid exceeds the surface temperature. Accordingly, the heat transfer rate from the surface decreases as shown in Fig. 5(b).
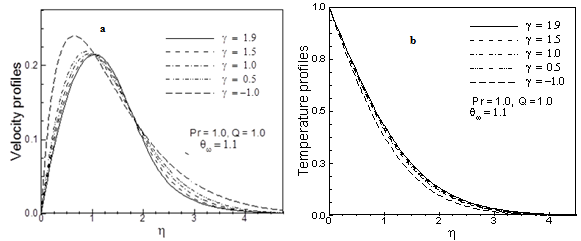 | Figure 2. (a) Velocity and (b) temperature profiles for different values of viscosity parameter γ with others fixed parameters |
 | Figure 3. (a) Velocity and (b) temperature profiles for different values of prandtl number Pr with others fixed parameters |
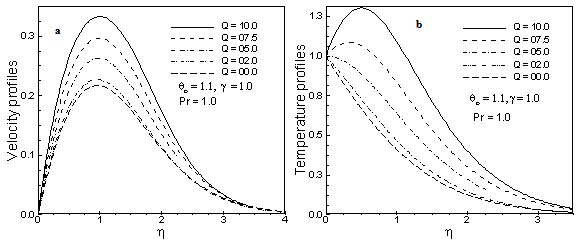 | Figure 4. (a) Velocity and (b) temperature profiles for different values of heat generation parameter Q with others fixed parameters |
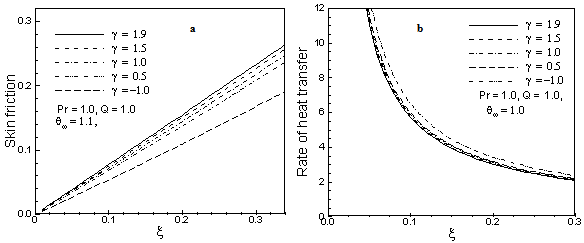 | Figure 5. (a) Skin friction and (b) rate of heat transfer for different values of viscosity parameter γ with others fixed parameters |
 | Figure 6. (a) Skin friction and (b) rate of heat transfer for different values of prandtl number Pr with others fixed parameters |
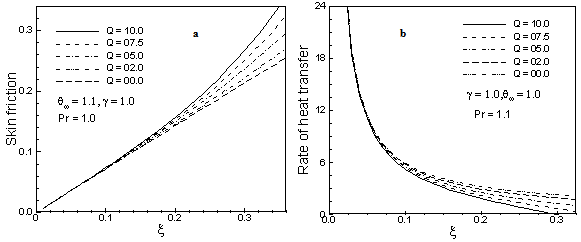 | Figure 7. (a) Skin friction and (b) rate of heat transfer for different values of heat generation parameter Q with others fixed parameters |
|
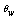 = 1.1, Q = 1.0 and γ =1.0 are shown in Figures 6(a)-6(b). We can observe from these figures that as the Prandtl number Pr increases, the skin friction coefficient decreases and rate of heat transfer increases.Figures 7(a)-7(b) show that skin friction coefficient Cfx increase and heat transfer coefficient Nux decreases for increasing values of heat generation parameter Q while viscosity parameter γ = 1.0,. Prandtl number Pr = 1.0 and surface temperature parameter θw = 1.1. The values of skin friction coefficient Cfx and Nusselt number Nux are recorded to be 0.26704, 0.25130, 0.23729. 0.22247, 0.21366 and 0.04986, 0.71367, 1.31147, 1.95384 and 2.34324 for Q = 10.0, 5.0, 7.5.2.0, 0.0 and respectively which occur at the same point ξ = 0.3. Here, it observed that at ξ = 0.3, the skin friction increases by 39.07% and Nusselt number Nux decreases by 97.87% as the heat generation parameter Q changes from 0.0 to 10.0. It is observed from figure 7(a) that the skin friction increases gradually from zero value at lower stagnation point along the ξ direction and from Figure 7(b); it reveals that the rate of heat transfer decreases along the ξ direction.Numerical values of rate of heat transfer Nux and skin friction coefficient Cfx are calculated from Equations (13) from the surface of the vertical porous plate. Numerical values of Cfx and Nux are shown in Table 1.In the above table 1 the values of skin friction coefficient Cfx and Nusselt number Nux are recorded to be 0.26704, 0.25130, 0.23729. 0.22247, 0.21366 and 0.04986, 0.71367, 1.31147, 1.95384 and 2.34324 for Q = 10.0, 5.0, 7.5.2.0, 0.0 and respectively which occur at the same point ξ = 0.3. Here, it observed that at ξ = 0.3, the skin friction increases by 39.07% and Nusselt number Nux decreases by 97.87% as the heat generation parameter Q changes from 10.0 to 0.0.
= 1.1, Q = 1.0 and γ =1.0 are shown in Figures 6(a)-6(b). We can observe from these figures that as the Prandtl number Pr increases, the skin friction coefficient decreases and rate of heat transfer increases.Figures 7(a)-7(b) show that skin friction coefficient Cfx increase and heat transfer coefficient Nux decreases for increasing values of heat generation parameter Q while viscosity parameter γ = 1.0,. Prandtl number Pr = 1.0 and surface temperature parameter θw = 1.1. The values of skin friction coefficient Cfx and Nusselt number Nux are recorded to be 0.26704, 0.25130, 0.23729. 0.22247, 0.21366 and 0.04986, 0.71367, 1.31147, 1.95384 and 2.34324 for Q = 10.0, 5.0, 7.5.2.0, 0.0 and respectively which occur at the same point ξ = 0.3. Here, it observed that at ξ = 0.3, the skin friction increases by 39.07% and Nusselt number Nux decreases by 97.87% as the heat generation parameter Q changes from 0.0 to 10.0. It is observed from figure 7(a) that the skin friction increases gradually from zero value at lower stagnation point along the ξ direction and from Figure 7(b); it reveals that the rate of heat transfer decreases along the ξ direction.Numerical values of rate of heat transfer Nux and skin friction coefficient Cfx are calculated from Equations (13) from the surface of the vertical porous plate. Numerical values of Cfx and Nux are shown in Table 1.In the above table 1 the values of skin friction coefficient Cfx and Nusselt number Nux are recorded to be 0.26704, 0.25130, 0.23729. 0.22247, 0.21366 and 0.04986, 0.71367, 1.31147, 1.95384 and 2.34324 for Q = 10.0, 5.0, 7.5.2.0, 0.0 and respectively which occur at the same point ξ = 0.3. Here, it observed that at ξ = 0.3, the skin friction increases by 39.07% and Nusselt number Nux decreases by 97.87% as the heat generation parameter Q changes from 10.0 to 0.0.5. Comparison of the Results
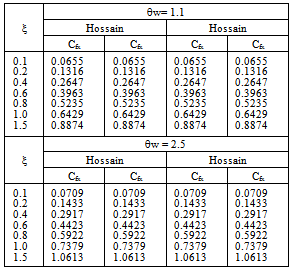
- In order to verify the accuracy of the present work, the values of Nusselt number and skin friction for Q=0, Rd=0.05.Pr=1.0, γ = 0 and various surface temperature
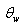 =1.1,
=1.1, 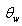 =2.5 at different position of
=2.5 at different position of 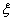 are compared with Hossain[9] as presented in Table 2. The results are found to be in excellent agreement.
are compared with Hossain[9] as presented in Table 2. The results are found to be in excellent agreement.6. Conclusions
- For different values of relevant physical parameters including the viscosity parameter γ , the effect of radiation on natural convection flow from a porous vertical plate in presence of heat generation has been investigated. The governing boundary layer equations of motion are transformed into a non-dimensional form and the resulting non-linear systems of partial differential equations are reduced to local non-similarity boundary layer equations, which are solved numerically by using implicit finite difference method together with the Keller-box scheme. From the present investigation the following conclusions may be drawn:• Significant effects of heat generation parameter Q and viscosity parameter γ on velocity and temperature profiles as well as on skin friction coefficient Cfx and the rate of heat transfer Nux have been found in this investigation but the effect of heat generation parameter Q and viscosity parameter γ on rate of heat transfer is more significant. An increase in the values of viscosity parameter γ leads to the velocity decrease and the temperature profiles increase, the local skin friction coefficient Cfx increase and the local rate of heat transfer Nux decreases at different position of ξ for Pr =1.0.• For increasing values of Prandtl number Pr leads to decrease the velocity profile, the temperature profile and the local skin friction coefficient Cfx but the local rate of heat transfer Nux increases. • An increase in the values of Q leads to increase the velocity profiles and the temperature profiles and also the local skin friction coefficient Cfx increase but the local rate of heat transfer Nux decreases.
Nomenclatures

Greek symbols

Subscripts

References
| [1] | J. Merkin, “Free convection with blowing and suction,” Int. J. Heat Mass Transf., vol. 15, no. 5, pp. 989–999, May 1972. |
| [2] | H.-T. Lin and W.-S. Yu, “Free Convection on a Horizontal Plate With Blowing and Suction,” J. Heat Transf., vol. 110, no. 3, pp. 793–796, Aug. 1988. |
| [3] | M. A. Hossain, K. Khanafer, and K. Vafai, “The effect of radiation on free convection flow of fluid with variable viscosity from a porous vertical plate,” Int. J. Therm. Sci., vol. 40, no. 2, pp. 115–124, Feb. 2001. |
| [4] | M. A. Hossain, M. S. Munir, and D. A. S. Rees, “Flow of viscous incompressible fluid with temperature dependent viscosity and thermal conductivity past a permeable wedge with uniform surface heat flux,” Int. J. Therm. Sci., vol. 39, no. 6, pp. 635–644, Jun. 2000. |
| [5] | M. A. Hossain and H. S. Takhar, “Radiation effect on mixed convection along a vertical plate with uniform surface temperature,” Heat Mass Transf., vol. 31, no. 4, pp. 243–248, Apr. 1996. |
| [6] | M. M. Molla, M. A. Hossain, and L. Shin Yao, “Natural convection flow along a vertical wavy surface with uniform surface temperature in presence of heat generation/ absorption,” Int. J. Therm. Sci., vol. 43, no. 2, pp. 157–163, Feb. 2004. |
| [7] | T. Akhter, “Effect of Radiation on Natural Convection Flow on a Sphere with Isothermal surface and uniform Heat Flux,” Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh, 2007. |
| [8] | M. M. Ali, “Numerical Study of Radiation on Natural Convection Flow on a Sphere with Heat Generation,” Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh, 2007. |
| [9] | M. A. Hossain, M. A. Alim, and D. A. S. Rees, “The effect of radiation on free convection from a porous vertical plate,” Int. J. Heat Mass Transf., vol. 42, no. 1, pp. 181–191, Jan. 1999. |
| [10] | K. Vajravelu and A. Hadjinicolaou, “Heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation,” Int. Commun. Heat Mass Transf., vol. 20, no. 3, pp. 417–430, May 1993. |
| [11] | M. M. Molla, M. A. Hossain, and M. A. Taher, “Magnetohydrodynamic natural convection flow on a sphere with uniform heat flux in presence of heat generation,” Acta Mech., vol. 186, no. 1–4, pp. 75–86, Oct. 2006. |
| [12] | J. Gary, D. R. Kassoy, H. Tadjeran, and A. Zebib, “The effects of significant viscosity variation on convective heat transport in water-saturated porous media,” J. Fluid Mech., vol. 117, pp. 233–249, 1982. |
| [13] | K. N. Mehta and S. Sood, “Transient free convection flow with temperature dependent viscosity in a fluid saturated porous medium,” Int. J. Eng. Sci., vol. 30, no. 8, pp. 1083–1087, Aug. 1992. |
| [14] | N. G. Kafoussias and E. W. Williams, “The effect of temperature-dependent viscosity on free-forced convective laminar boundary layer flow past a vertical isothermal flat plate,” Acta Mech., vol. 110, no. 1–4, pp. 123–137, Mar. 1995. |
| [15] | N. G. Kafoussias, D. a. S. Rees, and J. E. Daskalakis, “Numerical study of the combined free-forced convective laminar boundary layer flow past a vertical isothermal flat plate with temperature-dependent viscosity,” Acta Mech., vol. 127, no. 1–4, pp. 39–50, Mar. 1998. |
| [16] | M. A. Hossain, S. Kabir, and D. A. S. Rees, “Natural convection of fluid with variable viscosity from a heated vertical wavy surface,” Z. Für Angew. Math. Phys. Zamp, vol. 53, no. 1, pp. 48–57, 2002. |
| [17] | M. A. Hossain and M. S. Munir, “Mixed convection flow from a vertical flat plate with temperature dependent viscosity,” Int. J. Therm. Sci., vol. 39, no. 2, pp. 173–183, Feb. 2000. |
| [18] | V. P. Carey and J. C. Mollendorf, “Natural convection in liquid with temperature dependent viscosity,” in 6th International Heat Transfer Conference, 1978, vol. 2. |
| [19] | H. B. Keller, “Numerical Methods in Boundary-Layer Theory,” Annu. Rev. Fluid Mech., vol. 10, no. 1, pp. 417–433, 1978. |
| [20] | T. Cebeci and P. Bradshaw, Physical and Computational Aspects of Convective Heat Transfer. Springer, 1991. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML