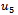| [1] | G.Adomian,Solving Frontier Problems of Physics :the Composition Method. Kluwer, Boston, 1994. |
| [2] | J.I.Ramos, Piecewise-adaptive decomposition methods. Chaos,Solitons and Fractals 198(1)(2008)92. |
| [3] | F. Khani, M. Ahmadzadeh Raji, H. Hamedi Nejad, Analytical solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient, Commun. Nonlinear Sci. Numer. Simul. 14 (2009) 3327_3338. |
| [4] | A. Molabahrami, F. Khani, The homotopy analysis method to solve the Burgers-Huxley equation, Nonlinear Anal. RWA 10 (2) (2009) 589_600. |
| [5] | M. Sajid, I. Ahmad, T. Hayat, M. Ayub, Unsteady flow and heat transfer of a second grade fluid over a stretching sheet, Commun. Nonlinear Sci. Numer.Simul. 14 (1) (2009) 96_108. |
| [6] | F. Khani, M. Ahmadzadeh Raji, S. Hamedi-Nezhad, A series solution of the fin problem with a temperature-dependent thermal conductivity, Commun.Nonlinear Sci. Numer. Simul. 14 (2009) 3007_3017. |
| [7] | F. Khani, A. Farmany, M. Ahmadzadeh Raji, A. Aziz, F. Samadi, Analytic solution for heat transfer of a third grade viscoelastic fluid in non-Darcy porous media with thermophysical effects, Commun. Nonlinear Sci. Numer. Simul. (2009) doi:10.1016/j.cnsns.2009.01.031. |
| [8] | F. Khani, A. Aziz, Thermal analysis of a longitudinal trapezoidal fin with temperature dependent thermal conductivity and heat transfer coefficient, Commun. Nonlinear Sci. Numer. Simul (2009), doi:10.1016/j.cnsns.2009.04.028. |
| [9] | J.H.He,Variational iteration method: a kind of nonlinear analytical technique :some example.International Journal of NonLinear Mechanics34(4)(1999)699. |
| [10] | J.H.He,X.H.Wu,Construction of solitary solution and compaction-like solution by variation iteration method. Chaos.Solitons&Fractals29(2006)108. |
| [11] | D.D.Ganji,HafezTari,H.Babazadeh,The application of He’s variational iteration method to nonlinear equations arising in heat transfer.Physics Letters A 363 (3)(2007)213. |
| [12] | M.Rafei,D.D.Ganji,H.Daniali,H.Pashaei,Thevariationaliterationmethodfornonlinear oscillatorswithdiscontinuities.JournalofSoundandVibration305 (2007) 614. |
| [13] | J.H.He,The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation151 (1)(2004)287. |
| [14] | J.H.He,Homotopy perturbation method for bifurcation on nonlinear problems.International Journal of Nonlinear Sciences and Numerical Simulation6 (2005) 207. |
| [15] | D.D.Ganji,A.Sadighi,Application of He’s homotopy perturbation method to nonlinear coupled systems of reaction diffusion equations .International Journal of Nonlinear Sciences and Numerical Simulation7(4)(2006)411. |
| [16] | M.Rafei,D.D.Ganji,Explicit solutions of Helmholtz equation and fifth-order KdV equation using homotopy perturbation method .International Journal of Nonlinear Sciences and Numerical Simulation7(3)(2006)321. |
| [17] | T.Özis,A.Yildirim,Acomparative study of He’s homotopy perturbation method for determining frequency amplitude relation of an on linear oscillator with discontinuities. International Journal of Nonlinear Sciences and Numerical Simulation8(2)(2007)243. |
| [18] | A.Beléndez,C.Pascual,S.Gallego,M.Ortuño,C.Neipp, Application of a modified He’s homotopy perturbation method to obtain higher-order approximations of an x1/3 force nonlinear oscillator.PhysicsLettersA371 (2007) 421. |
| [19] | J.H.He,Non-perturbative Methods for Strongly Nonlinear Problems, Dissertation, deVerlagim Internet GmbH,2006. |
| [20] | M.Dehghan ,F.Shakeri , Solution of an integro-differential equation arising in oscillating magnetic fields using He’s homotopy perturbation method .Progress in Electromagnetic Research ,PIER78(2008)361. |
| [21] | M.Dehghan,F.Shakeri,The numerical solution of the second Painlev equation. Numerical Method for Partial Differential Equations 25(2009)1238. |
| [22] | M.Dehghan,J.Manafian,The solution of the variable coefficients fourth-order parabolic partial differential equations by the homotopy perturbation method. ZeitschriftfuerNatur for schung A64a(2009)411. |
| [23] | F.Soltanian,M.Dehghan,S.M.Karbassi, Solution of the differential algebraic equations via homotopy perturbation method and their engineering applications, International Journal of Computer Mathematics ,inpress, doi:10. 1080/00207160802545908. |
| [24] | A.Saadatmandi,M.Dehghan,A.Eftekhari,Application of He’s homotopy perturbation method for nonlinear system of second-order boundary value problems. Nonlinear Analysis : Real World Applications 10(2009)1912. |
| [25] | F.Shakeri,M.Dehghan,Solution of delay differential equations via a homotopy perturbation method. Mathematical and Computer Modelling 48(2008) 486. |
| [26] | F.Shakeri,M.Dehghan,Inverse problem of diffusion equation by He’s homotopy perturbation method. Physica Scripta75(2007)551. |
| [27] | M.Dehghan,F.Shakeri,Solution of a partial differential equation subject to temperature over specification by He’s homotopy perturbation method. Physica Scripta 75(2007)778. |
| [28] | M.Dehghan,F.Shakeri, Use of He’s homotpy perturbation method for solving a partial differential equation arising in modeling of flow in porous media. Journal of Porous Media 11(2008)765. |
| [29] | E.N. Aksan, Appl. Math. Comput. 174 (2006) 884. |
| [30] | S. Kutluay, A. Esen, Int. J. Comput. Math. 81 (2004) 1433. |
| [31] | S. Abbasbandy, M.T. Darvishi, Appl. Math. Comput. 163 (2005) 1265. |
| [32] | Sirendaoreji, J. Phys. A: Math. Gen. 32 (1999) 6897. |
| [33] | B. Tian, Y. Gao, J. Phys. A: Math. Gen. 29 (1996) 2895. |
| [34] | H. Bateman, Mon. Weather Rev. 43 (1915) 163. |
| [35] | J.M. Burgers, Proc. R. Nether. Acad. Sci. Amsterdam 43 (1940) 2. |
| [36] | E. Hopf, Commun. Pure Appl. Math. 3 (1950) 201. |
| [37] | J.D. Cole, Quart. Appl. Math. 9 (1951) 225. |
| [38] | E.R. Benton, G.W. Platzman, Quart. Appl. Math. 30 (1972) 195. |
| [39] | V.I. Karpman, Nonlinear Waves in Dispersive Media, Pergamon, Oxford, 1975. |
| [40] | Cole, J. D., On a quasilinear parabolic equation occurring in aerodynamics, Quart. Appl. Math., Vol. 9, No. 3, pp. 225–236, 1951. |
| [41] | Ibragimov, N. H. (Editor), CRC Handbook of Lie Group Analysis of Differential Equations, Vol. 1, Symmetries, Exact Solutions and Conservation Laws, CRC Press, Boca Raton, 1994. |
| [42] | Polyanin, A. D. and Zaitsev, V. F., Handbook of Nonlinear Partial Differential Equations , Chapman & Hall/CRC, Boca Raton, 2004. |
| [43] | E.Hesameddini, H.Latifizadeh, Reconstruction of Variational Iteration Algorithms using the Laplace Transform, Int. J. Nonlinear Sci. Numer. Simul. 10 (2009)1377-1382 |

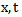 are two independent variables; consider
are two independent variables; consider  as the principal variable and
as the principal variable and 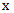 as the secondary variable. If
as the secondary variable. If 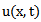 is a function of two variables
is a function of two variables 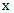 and
and 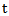 , when the Laplace transform is applied with
, when the Laplace transform is applied with 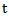 as a variable, definition of Laplace transform is
as a variable, definition of Laplace transform is 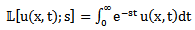
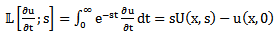
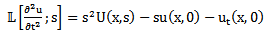

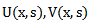 where
where 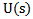 and
and 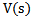 are known to the transform of the functions
are known to the transform of the functions 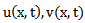 respectively. The convolution of
respectively. The convolution of 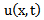 and
and 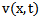 is written
is written 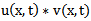 . It is defined as the integral of the product of the two functions after one is reversed and shifted. Convolution Theorem: if
. It is defined as the integral of the product of the two functions after one is reversed and shifted. Convolution Theorem: if 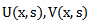 are the Laplace transform of
are the Laplace transform of 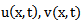 , when the Laplace transform is applied to
, when the Laplace transform is applied to 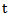 as a variable, respectively; then
as a variable, respectively; then 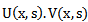 is the Laplace Transform of
is the Laplace Transform of 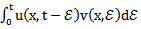
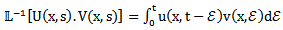
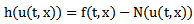 and considering the new equation, rewrite
and considering the new equation, rewrite 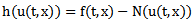 as
as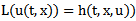
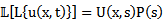
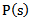 is polynomial with the degree of the highest order derivative of the selected linear operator.
is polynomial with the degree of the highest order derivative of the selected linear operator. 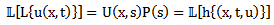
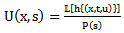
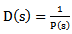 , and
, and 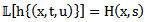 . Therefore using the convolution theorem we have
. Therefore using the convolution theorem we have 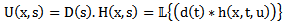
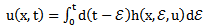
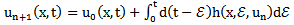
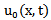 is initial solution with or without unknown parameters. In absence of unknown parameters,
is initial solution with or without unknown parameters. In absence of unknown parameters, 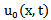 should satisfy initial/ boundary conditions.
should satisfy initial/ boundary conditions.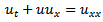
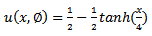
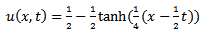
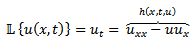
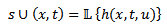
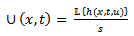
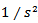 is as follows
is as follows 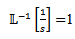
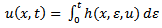
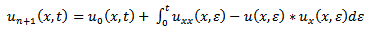
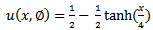
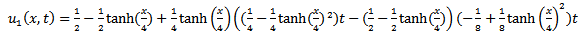
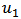 and
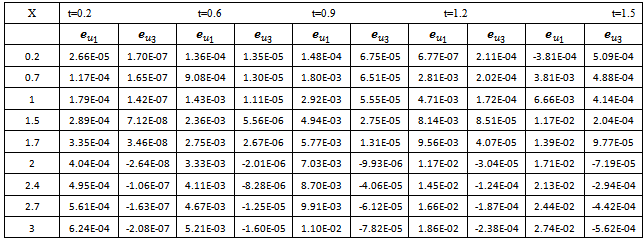
and 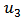 are expressed. The error of u has strong relevance to two independent parameters, x and t. x range is chosen between 0.2 to 3 and t is between 0.2 to 1.5, error depends on various amounts of x and t. as a mention the difference between errors of
are expressed. The error of u has strong relevance to two independent parameters, x and t. x range is chosen between 0.2 to 3 and t is between 0.2 to 1.5, error depends on various amounts of x and t. as a mention the difference between errors of 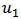 and
and 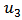 is noticeable.
is noticeable. 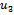 and
and 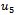 are illustrated in table2. like last state the amounts of errors depend on parameters x and t. to simulate more and show good enhancement in result, the ranges of x and t are chosen similar to the previous table (table 1.).as it is seen in comparison to table 1. the amounts of errors are showing a great reduction and this reduction is considerable between
are illustrated in table2. like last state the amounts of errors depend on parameters x and t. to simulate more and show good enhancement in result, the ranges of x and t are chosen similar to the previous table (table 1.).as it is seen in comparison to table 1. the amounts of errors are showing a great reduction and this reduction is considerable between 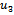 and
and 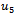 .u1 u3 u5 and the tables above are selected in a way to demonstrate the accuracy, efficiency and authenticity of the method for sequent stages.
.u1 u3 u5 and the tables above are selected in a way to demonstrate the accuracy, efficiency and authenticity of the method for sequent stages. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML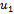 and
and 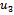
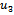 and
and