-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2013; 3(2): 39-44
doi:10.5923/j.am.20130302.01
What Could Happen, Will Happen? A Mathematical Proof and an Application to the Creation of Our Sub-universe
Yew-Kwang Ng
Winsemius Professor in Economics, Nanyang Technological University, Singapore 637332, NG
Correspondence to: Yew-Kwang Ng, Winsemius Professor in Economics, Nanyang Technological University, Singapore 637332, NG.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A valid proof of such ‘laws’ as ‘What could happen, will happen’ is impossible as they are false. This paper demonstrates this falsehood (Section 1), provides (Section 2) a formal and valid proof of the qualified law: What could happen with non-vanishing (i.e. positive and finite) probabilities, will happen (given sufficient time), and discusses several special cases with specific mathematical probabilities (Section 3). The appendix provides an application of the central result to a very interesting issue of the origin of our universe, proving that it was created, unless another identical one was created.
Keywords: What Could Happen, Finite, Probability, Creation, Universe
Cite this paper: Yew-Kwang Ng, What Could Happen, Will Happen? A Mathematical Proof and an Application to the Creation of Our Sub-universe, Applied Mathematics, Vol. 3 No. 2, 2013, pp. 39-44. doi: 10.5923/j.am.20130302.01.
Article Outline
1. Introduction
- This paper applies simple maths of probability to tackle some interesting and fundamental questions including Murphy’s law and the origin of our universe.The statement ‘What could happen, will happen’ is taken to mean that anything that has a positive probability of happening will certainly happen, sooner or later. This has been attributed to the Greek philosopher Diodorus but his works have been lost. The statement may also be taken as sounding like the well-known Murphy’s law (after Captain Edward A. Murphy, 1918-1990). However, this law actually says: ‘What could go wrong, will go wrong.’ (See[1],[2]). A much earlier similar law is due to Thomas Aquinas (1225 - 1274): “quia quod possible est non esse, quandoque non est.” (Summa Theologiae, I, q. 2, a. 3, corpus. Translation by Prof. Dr. Gerald J. Massey: “what is possible not to be, at some time does not exist.”) (See[3],[4],[5]). Whatever the degree of similarity or oppositeness! The present writer knows of no formal proof of such laws, though some support for Murphy’s law in terms of the tendency to go wrong has been provided by showing ‘that toast does indeed have an inherent tendency to land butter-side down for a wide range of conditions. Furthermore, … this outcome is ultimately ascribable to the values of the fundamental constants’[6]. In fact a formal and valid proof of such laws is impossible, as, without some appropriate revision/qualification, all such laws, including the one in the title of this paper (What could happen, will happen), are false. Obviously, one cannot validly prove that something false is true. This paper proves this falsehood (Section 2), provides (Section 3) a formal and valid proof of the qualified law: What could happen with non-vanishing probabilities, will happen (given sufficient time), and discusses several specific special cases (Section 4). The appendix provides an application of the central result to the very interesting issue on the origin of our universe, proving that it was created, unless another identical one was created.
2. The Unqualified Laws are False
- We may use a general notation x to stand for whatever that is supposed to ‘happen’, to ‘not exist’, to ‘go wrong’, etc. Then, the demonstration of the falsehood of such unqualified laws below applies to all such laws.‘What could happen’, or ‘what can go wrong’, etc. may be taken to mean that the probability of x happening in any time period is positive. For simplicity, we only consider non-degenerate period. In other words, the time periods are periods proper, not just points in time. (If time has a finite minimum unit as some quantum theorists believe, we may just take each of the non-degenerate periods concerned as no smaller than this very small unit. Then, the argument in this paper is not affected.) Denote the probability of x NOT happening in period i as pi and that of the probability of x happening in period i as 1 - pi. (This is to reduce mathematical complexity below as it is the probability of not happening that is used more often.) A common (not strictly valid) proof of these laws is to (usually implicitly) assume that this probability remains constant through time. Then, we may drop the subscript i and just use the constant probability p. Under the simplification of a constant and independent (of what happen in previous periods) probability, it is easy to see that the probability of x not happening in one or the first period is p, the probability of x not happening in both the first and second periods is p2, and the probability of x not happening in all the first t periods is pt. In contrast, the probability of x happening at least once is 1 minus the probability of x not happening, as these two events exhaust all possibilities. Thus, the probability of x happening at least once over t periods is 1 - pt. This probability approaches one as t approaches infinity since pt approaches zero as t approaches infinity. Thus, what could go wrong will go wrong; what could happen will happen for sure, sooner or later. This is usually the formal proof offered for Murphy’s law or other similar laws. For the unqualified law, the proof fails as shown by the following counter-example. [One counter-example is sufficient to falsify a general proposition.] Suppose a certain event has an independent probability of happening in the first period of 0.1, of happening in the second period of 0.01, of happening in the third period of 0.001, and so on. In other words, the probability of this event happening in any period t is independent to each other and equals 1/10t. It is clear that the probability of this event happening at least once is no larger than 0.111111….. This is so because 0.11111….. is the probability of the event happening in period 1 plus that in period 2 plus that in period 3 through to infinity. This sums to something more than the probability of happening at least once because some of the probabilities are counted more than once.To see this point, consider a simple case of just two periods. If the probability of an event happening in either is independent and the same at 0.2. The probability of it happening at least once is equals 1 – 0.82 = 0.36. This is smaller than 0.2 + 0.2 = 0.4 by the doubly counted probability of 0.2 by 0.2 = 0.04. If the event already happens in period 1, that it also happens in period 2 does not increase the probability of happening at least once.Coming back to the case of 1/10t discussed in the paragraph preceding the previous one, the probability of the event happening at least once is less than 0.11111111…… no matter how long time is allowed. Thus, the probability of the event not happening at all is larger than 0.888… or close to 90% (89% to be more precise). In fact, we may increase this probability of the event not happening at all to as high a value approaching one (but not equaling one) as we like. For example, instead of consider the case of 1/10t , we may consider the case of 1/10t+3 for the probability of the event happening in period t. This gives the event happening in each successive period starting from the first as: 0.0001, 0.00001, 0.000001, etc. The probability of happening at least once accumulates to less than 0.0001111…. or about (or just over) 1% of 1% (or one out of ten thousands) no matter how long time is allowed. We do not call such tiny chance of happening as WILL happen, at most we say it MAY happen.As 0.0001, 0.00001, … are all positive probabilities, such events could happen. But we have just seen that this does not mean that they will happen. Thus, the unqualified Murphy-law type propositions are false. There are many examples of such loose statements. For example, ‘When there is an infinite time to wait then anything that can happen, eventually will happen’ ([7], p.300; italics original). However, such laws also have an element of truth; positive probabilities do accumulate/increase. However, to ensure that they accumulate to certainty/unity, we have to strengthen the condition a bit, as discussed below.
3. Accumulation towards Certainty of Non-vanishing Probabilities
- Consider an event that has a positive and finite probability of happening in any (non-generate) time period (i.e. a period of finite length like a micro-second, a day or a century). This probability may remain unchanged throughout or vary, but remains finite and positive, rather than decreasing towards zero as in the case discussed in the last section. We may define these as non-vanishing probabilities. In fact, we actually may allow it to be zero over certain finite number of periods each of a finite duration, provided this does not apply to all the remaining periods, the result is not affected, as these periods of zero probability may just be ‘taken out’, without affecting our following proposition.Proposition A (Accumulation towards certainty of non-vanishing probabilities): If the probability of a certain event happening in any period is positive and finite, except over a finite number of periods each of a finite duration (when it may become zero), the probability of the event happening at least once accumulates towards certainty (unity) as time increases towards infinity.Proof: The probability that the event will NOT happen at all, not even once, up to time period t may be written as:(A) p1p2p3……ptwhere pi is the probability that the event will NOT happen in period i. Given the pre-condition of our proposition, some of these pi’s for some periods may be equal to one, but only for some finite number of them, each of finite duration, each of the remaining ones is less than one by a positive and finite amount. Then, as t approaches infinity, the number of pi’s in (A) that are not equal to zero but are less than one by a finite amount approaches infinity. Thus, the value of the product in (A) approaches zero as t approaches infinity. The probability of the event happening at least once equals one minus the probability of the event not happening at all, i.e.(B) 1 - p1p2p3……ptwhich clearly approaches one as t approaches infinity. Q.E.D.The proof above is general. However, to provide concreteness, some special cases are discussed below where the probability concerned may be given more concrete specification. We shall consider first the simple case where the probability in each period remains unchanged and is independent of each other, then the dependence case with an unchanged degree of dependence, and then that with a changing degree.
4. Some Special Cases
4.1. The Independent Case
- With a constant and independent probability in each period, we may drop the subscript for time period and let the positive probability of a certain event happening in any period to be 1-p (which is positive and finite), and the probability of not happening as p (which is non-negative and less than one by a finite amount). For this simple independent case, and with p remaining unchanged in all periods, it is straightforward that we have the probability of not happening after t periods as pt and the probability of happening at least once as
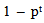 | (1) |
4.2. The Dependent Case, with an Unchanging (and Non-perfect) Degree of Dependence
- For the dependent case, first consider the simpler case where the (non-perfect) degree of dependence does not change with time.[If there are some finite periods each of a finite duration where the degree of dependence is perfect, these finite periods may be ‘taken out’ or ignored without affecting the results as discussed in the general proof above. If the perfect dependence persists indefinitely, it violates the pre-condition of the proposition.] We may write the probability of happening at least once after t periods as
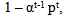 | (2) |
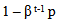 | (3) |
4.3. The Dependent Case, with a Changing (and Non-persistently Perfect) Degree of Dependence
- Now consider the case where the degree of dependence may change through time. We may divide this again into three sub-cases: A. Monotonically decreasing degree of dependence; B. Monotonically increasing degree of dependence; C. A variable degree of dependence. We have already proved in the previous section that, for any given (imperfect) degree of dependence, our proposition that a positive and finite probability accumulates towards unity in infinite time holds. Obviously, if this degree of dependence decreases, the probability of the event happening at least once accumulates faster than the case just discussed above and hence does not change our conclusion. Thus, our proposition of accumulation towards unity of positive probability holds for sub-case A.Now, consider sub-case B where the degree of dependence increases monotonically with time. Obviously, if the degree increases to become perfect dependence and remain so indefinitely, the probability will then stop accumulating. However, this violates the pre-condition of our proposition (as the probability vanishes to become zero). Thus, we just allow the degree to increase but never reach perfect dependence. This sub-case of monotonically increasing degree of dependence (but never reaches perfect dependence) may be modelled by taking β to be an increasing function of time t, but never reaches one.
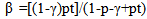 | (4) |
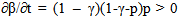 | (5) |
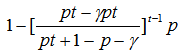 | (6) |
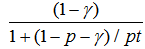 As t approaches infinity, the denominator approach one and the denominator remains unchanged at 1 – γ. Thus, this ratio is not only always smaller than one, it is smaller than one by at least a positive finite number γ. In (6), this bracketed ratio carries a power of t-1. Thus, as t increases to infinity, the powered ratio must thus shrinks towards zero. The whole expression in (6) must thus increases towards one as t approaches infinity.For the variable sub-case C, the degree of dependence may sometimes increases, sometimes remains unchanged, and sometimes decreases. When the degree of dependence either remains unchanged or decreases, this actually increases the speed of the accumulation of positive probability (in comparison to the case where the degree increases). Thus, this sub-case C of a variable degree of dependence must actually have faster speed of the accumulation of positive probability in comparison to some monotonically increasing one (without violating the precondition of the proposition). Our proposition must thus be still true for this sub-case C.
As t approaches infinity, the denominator approach one and the denominator remains unchanged at 1 – γ. Thus, this ratio is not only always smaller than one, it is smaller than one by at least a positive finite number γ. In (6), this bracketed ratio carries a power of t-1. Thus, as t increases to infinity, the powered ratio must thus shrinks towards zero. The whole expression in (6) must thus increases towards one as t approaches infinity.For the variable sub-case C, the degree of dependence may sometimes increases, sometimes remains unchanged, and sometimes decreases. When the degree of dependence either remains unchanged or decreases, this actually increases the speed of the accumulation of positive probability (in comparison to the case where the degree increases). Thus, this sub-case C of a variable degree of dependence must actually have faster speed of the accumulation of positive probability in comparison to some monotonically increasing one (without violating the precondition of the proposition). Our proposition must thus be still true for this sub-case C.5. Conclusions
- This paper demonstrates the falsehood of the proposition that what could happen will happen (Section 1), provides (Section 2) a formal and valid proof of a revised proposition: What could happen with non-vanishing (i.e. positive and finite) probabilities, will happen (given sufficient time), and discusses several special cases with specific mathematical probabilities (Section 3). The appendix provides an application of the central result to a very interesting issue of the origin of our universe, proving that it was created, unless another identical one was created.
Appendix
- An Application to the Creation of Our Sub-Universe Scientists told us that our universe originated about 14 billion years ago from a big bang, as confirmed in a letter signed by 255 leading scientists, members of the U.S. National Academy of Sciences, in [9]. But what made the Big Bang happen? From the following five compelling axioms which include Proposition A in the text, it is shown that God (defined just as the creator of our sub-universe) created our sub-universe (the observed universe from the Big Bang) or one identical to it. Before stating our axioms, a few simple definitions are needed.Definition 1: Our sub-universe is the universe we exist in and observe. Trusting our scientists, presumably it originated in the Big Bang about 14 billion years ago.Definition 2: The wider universe is the universe that includes our sub-universe and possibly whatever other things if they exist or existed. The wider universe includes everything any where in the past, the present, and the future.Definition 3: God is whatever or whoever created our sub-universe or one identical to it. Axiom 1: The Generalized First Law of Thermodynamics: Nothing comes from nothing. We first learned of the conservation of matter. After learning of the possibility of conversion between matter and energy (E=mc2), we generalized the law of conversation to matter and energy. If we find out in the future that matter and/or energy may be converted into something else, we may just generalize the conservation law correspondingly; Axiom 1 is still valid.Axiom 2: Accumulation of non-vanishing, positive probabilities towards certainty as time approaches infinity.This is Proposition A that has been proven in the text.Axiom 3: Things exist in the wider universe.From Descartes, we know that, I think, therefore I exist. We also know that things exist in our sub-universe from observation and scientific study. As the wider universe includes our sub-universe, so things must exist in the wider universe. If there is a bed in the bedroom, there must also be a bed in the house that contains that bedroom. If this axiom is false, the subject matter for this appendix does not exist.Axiom 4: Possibility of evolution: It is possible for non-living things to evolve into living things and for living things of simpler forms to evolve into more complex and more capable forms.The evidence for biological evolution on earth is compelling (see e.g.[10],[11]). Axiom 4 is much more compelling as it requires only some possibility, no matter how small (provided it is positive and finite) and no matter how slow (provided the speed is positive and finite). Even if a quintillion times slower than the speed of evolution on Earth in the last 4 billion years or so, this minimal requirement of Axiom 4 is sufficient for our purpose.Axiom 5: Possibility of Technology: After living things evolve to the level of Homo sapiens or beyond, it is possible (with positive and finite or non-vanishing probabilities) for such living things to use technology to improve their capability, possibly to a very high level difficult for us to imagine now.Again, this just requires some positive and finite possibility, could be very, very small and the speed in the advancement in technology could be very slow (but positive and finite). However, the level achieved could be very, very high. This does not rule out the possibility or even very high probability that, if such potentially dangerous technologies like nuclear power, cold fusion, genetic engineering, and some technology we cannot imagine now are used, 99.99% of the occasions result in disasters, including the extinction of that high-tech using being, or even of all living things. However, Axiom 5 here only requires that there is some positive and finite probability that, in some possibly very rare occasions, very high capability may be achieved.Proposition B: Evolved-God Creationism: God evolved in the wider universe and created our sub-universe or one identical to it.Proof: From Axiom 3, things exist in the wider universe. From Axiom 1, nothing comes from nothing, so things that exist in the wider universe could not just prop up themselves from nothing. They must have existed for ever. The wider universe has an infinite past. From Axiom 4, it is possible that in some (not necessarily only one) corners of the wider universe, non-living things evolved into living things which evolved further into more capable living things. This evolution may be but need not be similar to that on our Earth which is based on carbon, water, inheritance, mutation, and natural selection. Whatever its basis or principle, it was likely to be much slower [if not, this favours our result or process even more] than the evolution on Earth which reached the level of Homo sapiens in less than 4 billion years. In the wider universe, perhaps 99.99999999% of the occasions of evolution ended up in black alleys, disasters, retrogressions, cyclic fluctuations, etc. However, it is possible that over say one trillion quintillion years, at some corner of the wider universe, the evolution reaches the height similar to or higher than Homo sapiens on Earth. Then, from Axiom 5, they may use technology to further enhance their capability. Again, perhaps 99.99999999% of the occasions of high-tech ventures ended up in disasters, retrogressions, etc. However, it is possible that over a period of a quintillion to the power of quintillion centuries, some such evolution and technology enhancement allows that high-tech being to reach a level beyond our imagination, to a level capable of creating the Big Bang or something similar to it. From Axiom 5, the probability for this event over a period of that length must be positive and finite but could be quite small, say 0.000000000000001%. However, over its infinite past, the wider universe has an infinite number of periods each of such length. From Axiom 5, the probabilities of that event over these infinite periods may be small but are positive and finite, not vanishing. Thus, from Axiom 2 or Proposition A in the text, these probabilities accumulate towards unity or certainty as the number of periods increases towards infinity. Thus, over the infinite past in the wider universe, it is certain that God evolved in the wider universe and created our sub-universe or another one identical to it. Q.E.D.Remark 1: This proposition explains the peculiar nature of the physics of our sub-universe, including its observance of the theory of relativity (including 0.99c + 0.99c < c where c is the speed of light) and quantum absurdities. For example, the quantum uncertainty is intrinsic and happens spontaneously without any cause. A pair of ‘entangled’ particles in two different places light-years apart involves instantaneous effects of the observation of one on the other (the quantum entanglement as confirmed by the Bell experiments; see, e.g.[12])! It also explains why the many constants of nature happen to be within the narrow ranges suitable for the evolution of stable systems of stars and of living things in certain planets; see[13],[14]. As Walker and Ćirković[15] conclude, after an examination of the relevant issues (including distinguishing between mathematical and anthropic fine tuning), ‘It appears that if the values of the fundamental constants of the universe are assigned randomly, then the chances of human life developing in this universe are astronomically small.’ If our (sub) universe was created, it may be more peculiar than a clock and designed to favour the evolution of living things. Though other explanations such as the multiverse may also explain the biofriendly ranges of the constants of nature, they do not seem to explain the peculiar nature of our sub-universe and they appear to assume more than the explanation here..Remark 2: It may be asked, who created the wider universe? By definition, the wider universe includes everything every where any time. Thus, if there was something that created the universe in which God [who created our sub-universe] evolved, that something must also be part of the wider or widest universe. Hence, by definition, the wider or widest universe cannot have a creator. It must exist by itself. From Axiom 1, it must also have existed from the infinite past. Nevertheless, the wider universe may be Newtonian like, without the peculiar relativistic and quantum physical peculiarities, and hence it was more like a rock and hence did not need a creator to explain its peculiar nature. But how could such a non-peculiar universe had evolution leading to God that created our peculiar sub-universe? It is not our knowledge that the principles of Darwinian evolution (inheritance, mutation, and natural selection) require either relativistic or quantum physical peculiarities. In a Newtonian like world, evolution may be terribly slow. But that disadvantage could be more than made up by the existence of an infinite amount of time. It is well-known that complexities may spring out from simplicities and chaos if just from sheer random changes. After the evolution of living things, additional forces are present for evolution towards more complex species from natural selection as witnessed in our planet. The evolution in the wider universe need not be exactly the same but this does not rule out evolution to a much higher level due to the sheer infinite amount of time available.Remark 3: Some religions also maintain that God exists by itself and is beyond time or even is supernatural. Why not just believe in such a supernatural God instead of believing in the wider universe and the evolution of God therein? Believing in the existence of God by itself does not only fail to answer the question where did God come from, it also destroys the strongest argument of God’s existence, the argument from design. A piece of rock needs no creator, but a clock needs a creator or some specific explanation. If our peculiar universe needs a creator or some explanation, the God that could create our universe needs a creator or some explanation with stronger force. If the clock is created a by a clock-making machine, who created that machine? It makes more sense to believe that the clock exists by itself than to believe that the clock-making machine exists by itself. On the other hand, it is sensible to believe that the possibly Newtonian-like wider universe may exist by itself as the Newtonian world is without relativistic and quantum physical peculiarities and hence is more like a rock.Remark 4: Our proposition B only proves the creation of our sub-universe or one identical to it. By identical, it means exactly the same in every aspect. If God created another sub-universe identical to ours, there must also be an exactly similar Earth in that other sub-universe with exactly the same set of billions of people not only of exactly similar names, addresses, birth days, and physical appearance but also of subjective thinking. There must also be an exactly same paper entitled ‘What Could Happen, Will Happen: A Mathematical Proof with An Application to the Creation of Our Sub-universe’ written and read by exactly the same set of individuals identical to those in our Earth in our sub-universe. Moreover, if you believe in this (that God created another sub-universe but our sub-universe was not created), you cannot explain the origin of the Big Bang, the origin of our sub-universe, why our physics is so peculiar, why the constants of nature are within a narrow ranges suitable for life, etc. But you still have to (unless you can refute our Proposition B) believe that God created a sub-universe identical to ours. Why not just believe that God created our sub-universe and have everything explained?
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML