M. E. Sayed-Ahmed1, H. K. Saleh2, Ibrahim Hamdy2
1Engineering Mathematics and Physics Department, Faculty of Engineering, Fayoum University, Egypt
2Engineering Mathematics and Physics Department Faculty of Engineering, Cairo University, Egypt
Correspondence to: M. E. Sayed-Ahmed, Engineering Mathematics and Physics Department, Faculty of Engineering, Fayoum University, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The problem of thermally laminar heat transfer based on the fully developed velocity for Bingham fluids in the entrance region of a circular duct is studied. The effect of the axial position, Peclet number, and Brinkman number are taken into account. Two cases of T (constant wall temperature) and H2 (constant heat flux) thermally boundary conditions are considered in this study. The energy equation is solved numerically by finite difference methods. The marching technique and the relaxation method are the main factors of the computer program. The results of the present work including the variation of the Nusselt number and mean temperature with the axial distance for the two cases are represented in Figures and compared with the available known results to support its accuracy.
Keywords:
Graetz Problem, Bingham Fluid, Circular Duct, Numerical Analysis
Cite this paper: M. E. Sayed-Ahmed, H. K. Saleh, Ibrahim Hamdy, Numerical Solution of the Extend Graetz Problem for a Bingham Plastic Fluid in Laminar Tube Flow, Applied Mathematics, Vol. 3 No. 1, 2013, pp. 27-37. doi: 10.5923/j.am.20130301.04.
1. Introduction
Many of the fluids used for industrial purposes are non-Newtonian such as pastes, polymer solutions and melts, plastics, pulps and emulsions in every day chemical engineering practice. Bingham model is one of the simplest models that describes materials with yield stress and most widely model for the above materials. Viscous dissipation changes the temperature distributions by playing a role like an energy source, which affects heat transfer rates. The merit of the effect of the viscous dissipation depends on whether the pipe is being cooled or heated. Many studies involving pipe flows in the existing literature have neglected the effect of viscous dissipation. In fact, the shear stresses can induce a considerable power generation. However, in the existing convective heat transfer literature, this effect is usually regarded as important only in two cases of flow in capillary tubes and flow of very viscous fluids. The effects of viscous dissipation in laminar flows have not yet been deeply investigated. For liquids with high viscosity and low thermal conductivity, disregarding the viscous dissipation can cause appreciable errors. The first studies of heat transfer in a duct flow of Newtonian fluid were made more than a century ago by Greatz in1883-1885 and independently by Nusselt in 1910. Solutions to this problem and its various extensions continue to evoke many research efforts and a comprehensive review of the works on heat transfer in laminar duct flow was compiled by Shah and London[1]. Tyagi[2] performed a wide study on the effect of viscous dissipation on the fully developed laminar forced convection in cylindrical tubes with an arbitrary cross-section and uniform wall temperature. Ou and Cheng[3] employed the separation of variables method to study the Graetz problem with finite viscous dissipation. They obtained the solution in the form of a series whose eigenvalues and eigenfunctions of which satisfy the Sturm–Liouville system. The solution technique follows the same approach as that applicable to the classical Graetz problem and therefore suffers from the same weakness of poor convergence behavior near the entrance. Lin et al.[4] showed that the effect of viscous dissipation was very relevant in the fully developed region if convective boundary conditions were considered. With these boundary conditions and if viscous dissipation was taken into account, the fully developed value of the Nusselt number was 48/5 for every value of the Biot number and of the other parameters. On the other hand, it is well known that, if a forced convection model with no viscous dissipation is employed, the fully developed value of the Nusselt number for convective boundary conditions depends on the value of the Biot number. Basu and Roy[5] analyzed the Graetz problem for Newtonian fluid by taking the account of viscous dissipation but neglecting the effect of axial conduction. Zanchini[6] analyzed the asymptotic behavior of laminar forced convection in a circular tube, for a Newtonian fluid at constant properties by taking into account the viscous dissipation effects. It was disclosed that particularly for the boundary conditions of uniform wall temperature and of heat transfer by convection to an external fluid yielded the same asymptotic behavior of the Nusselt number, namely Nu =48/5. And therefore, He obviously stated that, for these boundary conditions, when the wall heat flux qwً(x ( tended to zero, i.e., the local Brinkman number Br(x) tended to infinity, it is completely wrong to neglect the effect of viscous dissipation on the asymptotic behavior of the forced convection problem. Aydin[7] investigated the effect of viscous dissipation on thermally developed laminar forced convective flow in a pipe for a Newtonian fluid with constant properties. They showed that the effect of viscous dissipation could not be neglected when the wall temperature was uniform. The effect of viscous dissipation on the thermal entrance region in a pipe for a power law non-Newtonian fluid has been studied by Liou and Wang[8] using the uniform wall heat flux thermal boundary condition, Berardi et al.[9] using the convection with an external isothermal fluid, Lawal and Mujumdar[10] and Dang[11] using the uniform wall temperature. Barletta[12] studied the asymptotic behavior of the temperature flield for the laminar and hydrodynamically developed forced convection of a power-law fluid which flows in a circular duct taking the viscous dissipation into account. The asymptotic Nusselt number and the asymptotic temperature distribution were evaluated analytically in the cases of either the uniform wall temperature or convection with an external isothermal fluid. Also, Valko[13] studied the problem for power law fluid using the Laplace transform Galerkin technique. Khatyr et al.[14] investigated the fully developed laminar forced convection in circular ducts for a Bingham plastic with viscous dissipation and negligible axial heat conduction in the fluid. Both the asymptotic Nusselt number and the asymptotic profile temperature are obtained for many axial distributions of wall heat flux, which yield a thermally developed region. Min et al.[15] studied thermally fully developed flow of a Bingham plastic including axial conduction, to obtain the Nusselt number and temperature profiles and to propose a correlation formula between the Nusselt number and the Peclet number and also studied thermally developing flow (the Graetz problem) of a Bingham plastic including both axial conduction and viscous dissipation. The solution to this problem is obtained by using the method of separation of variables, where the resulting eigenvalue problem is solved approximately by using the method of weighted residuals.In this paper, we study the effects of the viscous dissipation and axial conduction on the thermal entrance for a Bingham fluid in a tube. The flow is assumed to be laminar, steady state and fully developed velocity. Two cases of T (constant wall temperature) and H2 (constant heat flux) thermally boundary conditions are considered. The energy equation is solved numerically by finite difference method to obtain the temperature distributions. Then the mean temperature an Nusselt number are computed for the two thermal boundary conditions
2. Formulation of the Problem
The circular tube configuration and boundary conditions are shown in Fig. 1. The flow is assumed to be laminar steady state, and incompressible with constant physical properties. The Bingham model is chosen to characterize the Non-Newtonian behavior of the fluid. The fluid enters the duct at uniform temperature Te and fully developed velocity u. The no-slip condition is applied at the circular tube walls and two cases of thermal boundary conditions; uniform wall temperature everywhere ( T ) and uniform heat flux axially as well as peripherally (H2) are assumed.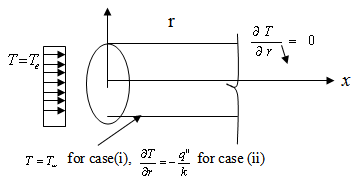 | Figure 1. Circular tube configuration and boundary conditions |
The energy equation for a circular tube with viscous dissipation and axial condation effect may be written as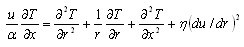 | (1) |
where 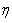 is the apparent viscosity for a Bingham model and given by
is the apparent viscosity for a Bingham model and given by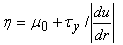 | (2) |
The boundary conditions of the problem for the two cases are given by:Case (i) T- thermal boundary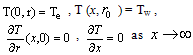 | (3) |
Case (ii) H2-thermal boundary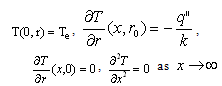 | (4) |
In addition to the non-dimensional variables, we may introduce the following: 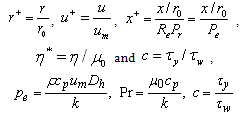 Where r0 is the radius of the tube, τw is the wall shear stress and Dh is the hydraulic diameter.The energy equation (1) is written in the following non-dimensional form by Min et al.[14] as
Where r0 is the radius of the tube, τw is the wall shear stress and Dh is the hydraulic diameter.The energy equation (1) is written in the following non-dimensional form by Min et al.[14] as 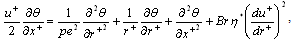 | (5) |
where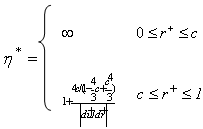 | (6) |
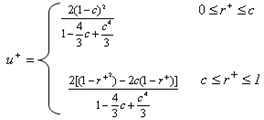 | (7) |
The boundary conditions of the problem for the two cases of thermal boundary conditions are written in the following non- dimensional forms:Case (i): 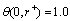 ,
, 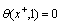 ,
, 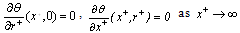 | (8) |
Case (ii): 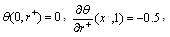
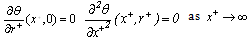 | (9) |
The local Nusselt numbers ,
, 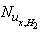 according to the two cases of the thermal boundary conditions are given by
according to the two cases of the thermal boundary conditions are given by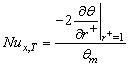 | (10) |
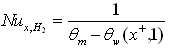 | (11) |
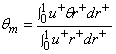 | (12) |
3. Numerical Solution
Using central difference for the L.H.S of the energy equation (5) and the Crank-Nicolson finite difference scheme for the R.H.S, the finite difference forms of the first and second derivatives are written as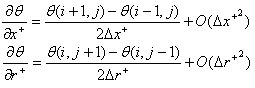 The finite-difference form of the energy equation (5) is:
The finite-difference form of the energy equation (5) is: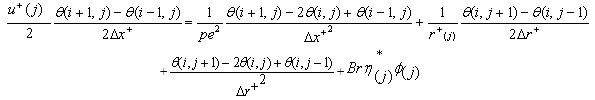 | (13) |
Where 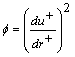 Rearranging equation (13) in the form as:
Rearranging equation (13) in the form as: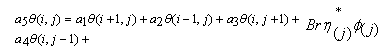 | (14) |
For 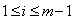 ,
, 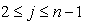 where ,
where , 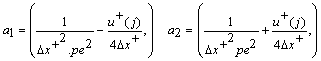
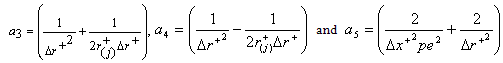 For
For 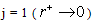 the term
the term 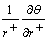 is undefined, therefore we apply the L’Hopital’s rule. Then
is undefined, therefore we apply the L’Hopital’s rule. Then 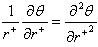 In the equation (13) becomes;
In the equation (13) becomes;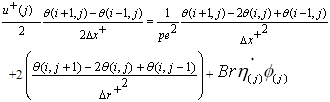 | (15) |
Rearranging equation (15) in the form as: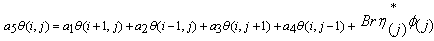 | (16) |
where ,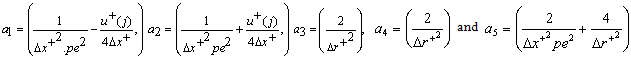 The difference forms of the boundary conditions are:For case (i):
The difference forms of the boundary conditions are:For case (i): 
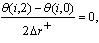
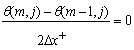 For case (ii):
For case (ii): 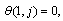
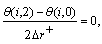
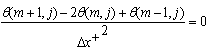 To compute Nusselt number and mean temperature for two cases of temperature boundary conditions we may introduce finite-difference forms for the integrals and the first partial derivatives in equations (10) and (12) .The Simpson rule for single integral is introduced by Jain et al.[16], is used to introduce a difference form for the integral equation (11) as
To compute Nusselt number and mean temperature for two cases of temperature boundary conditions we may introduce finite-difference forms for the integrals and the first partial derivatives in equations (10) and (12) .The Simpson rule for single integral is introduced by Jain et al.[16], is used to introduce a difference form for the integral equation (11) as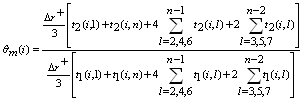 Where,
Where, 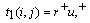
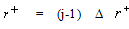 ,
, 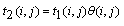
4. Method of Solution
The governing equations are solved numerically using the successive over relaxation method. For each axial position (i) (contain 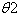 as unknown variable notation), in the first we get the velocity from equation (7), and the energy equation (14) is then solved to obtain
as unknown variable notation), in the first we get the velocity from equation (7), and the energy equation (14) is then solved to obtain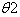 .The linear algebraic equations resulting from equation (14) may be written in the matrix form as
.The linear algebraic equations resulting from equation (14) may be written in the matrix form as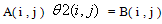 | (17) |
Where,A( i , j ) : Designate the coefficients of the unknowns in the algebraic equations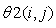 : Designate the unknowns in the algebraic equationsB( i , j ) : Designate the residual in the algebraic equationsi = 1,2,3,…………,n and j=1,2,3,…………,mThe relaxation equation can be written in the form of :
: Designate the unknowns in the algebraic equationsB( i , j ) : Designate the residual in the algebraic equationsi = 1,2,3,…………,n and j=1,2,3,…………,mThe relaxation equation can be written in the form of :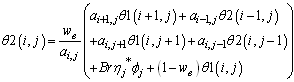 | (18) |
Where: : Known values of the temperature in the old iterations,
: Known values of the temperature in the old iterations, : Unknown values of the temperature in the new iterations,
: Unknown values of the temperature in the new iterations, : Relaxation factor,a: the coefficient of
: Relaxation factor,a: the coefficient of  .The resulting of a linear algebraic system of equations are solved by using successive over relaxation method (S.O.R) with relaxation factor
.The resulting of a linear algebraic system of equations are solved by using successive over relaxation method (S.O.R) with relaxation factor 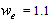 . The process repeated up till the difference between the new and old temperature value at each point is less than
. The process repeated up till the difference between the new and old temperature value at each point is less than 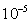 .
.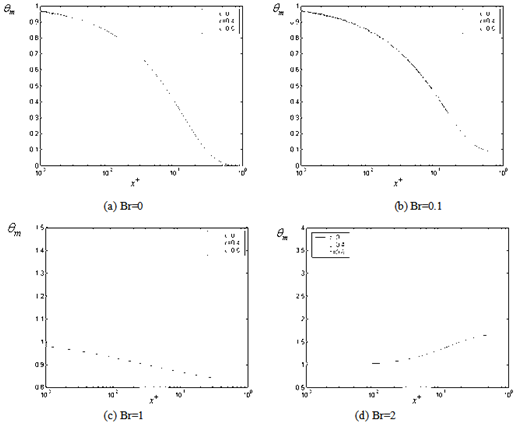 | Figure 2. The variation of the dimensionless mean temperature with respect to axial distance for Pe =100 (for case(i)) |
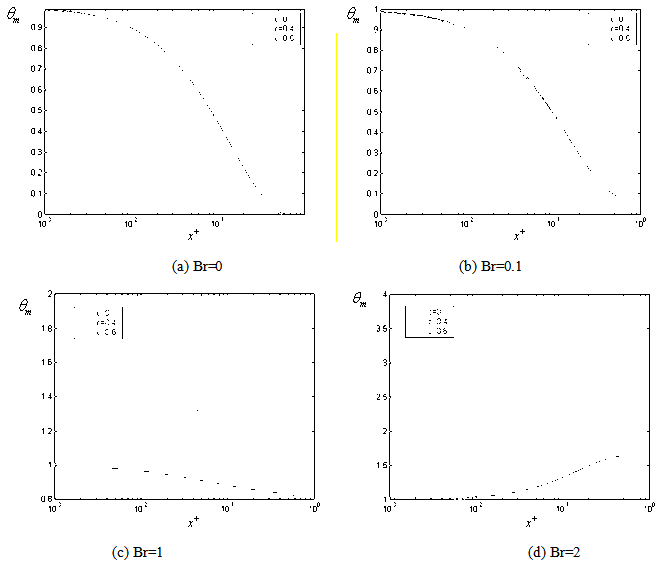 | Figure 3. The variation of the dimensionless mean temperature with respect to axial distance for Pe =10 (for case (i) ) |
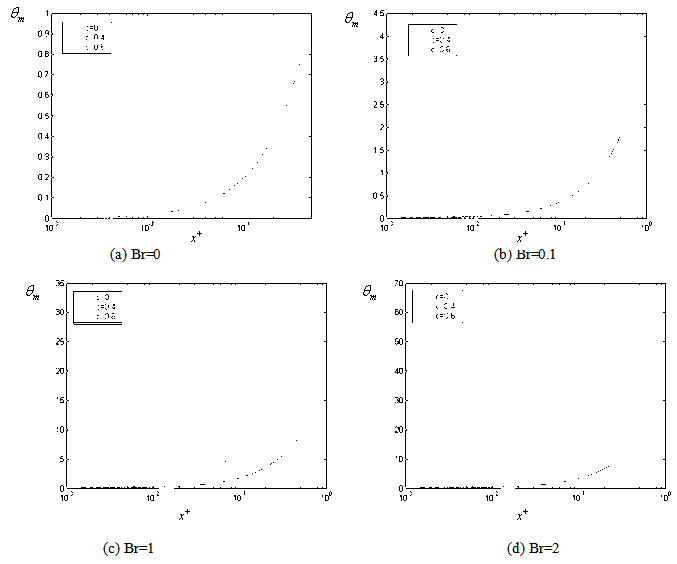 | Figure 4. The variation of the dimensionless mean temperature with respect to axial distance for Pe =100 (for case (ii) ) |
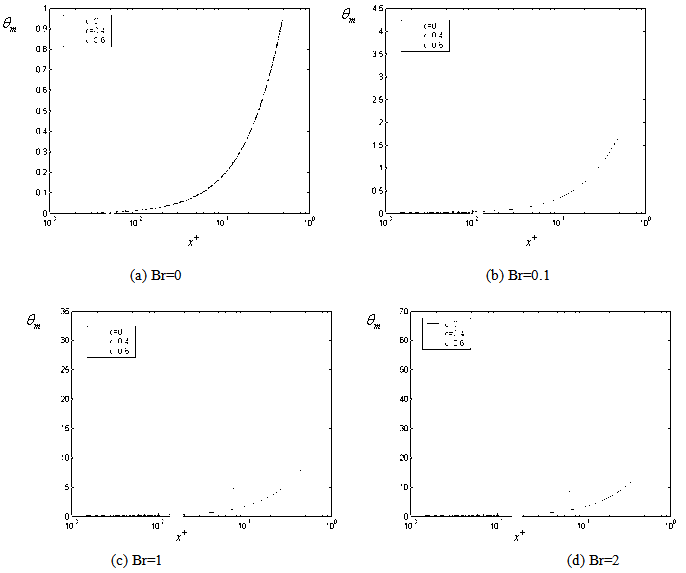 | Figure 5. The variation of the dimensionless mean temperature with respect to axial distance for Pe =10 (for case (ii) ) |
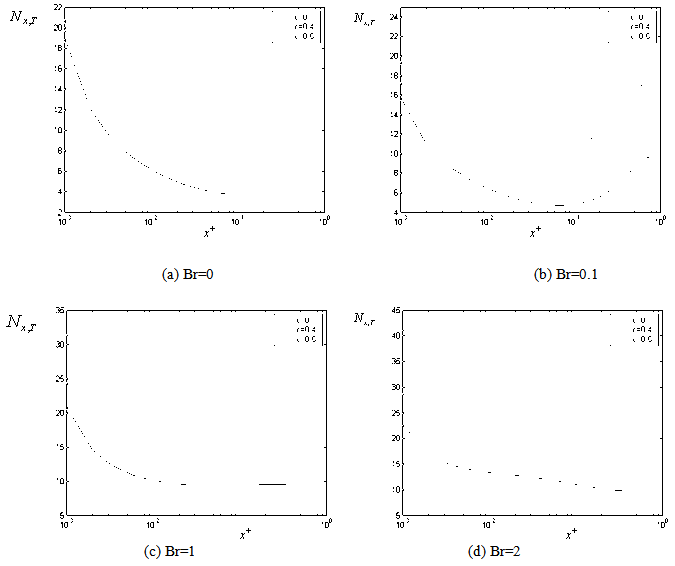 | Figure 6. The variation of the dimensionless local Nusselt number with respect to axial distance for Pe =100 (for case (i) ) |
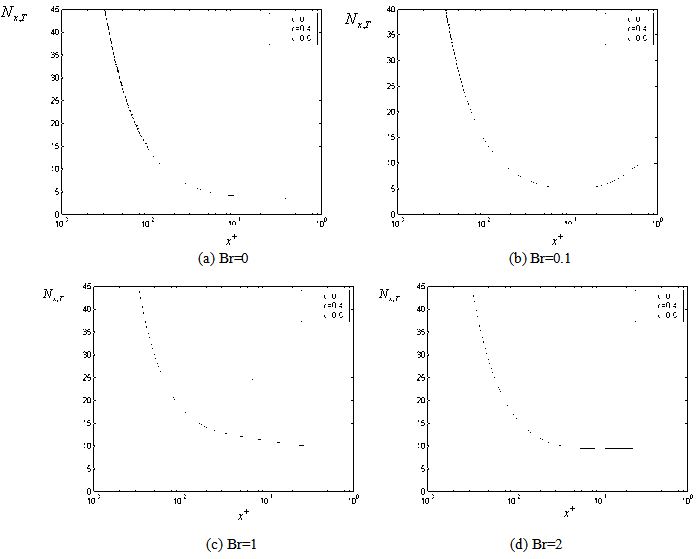 | Figure 7. The variation of the dimensionless local Nusselt number with respect to axial distance for Pe =10 (for case (i) ) |
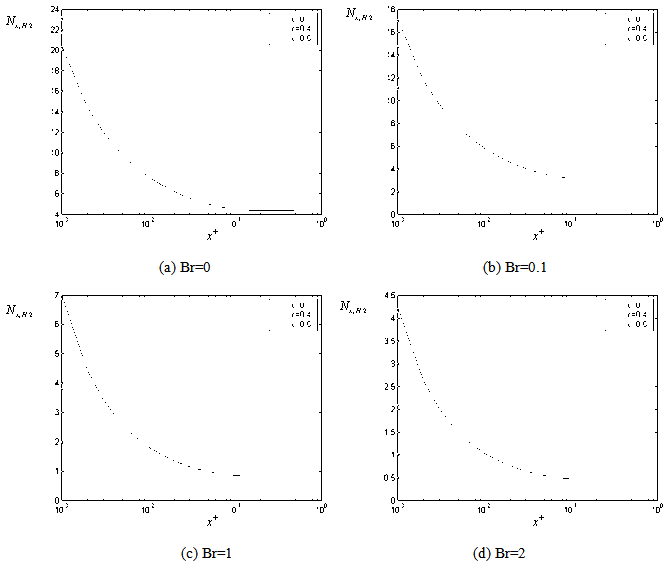 | Figure 8. The variation of the dimensionless local Nusselt number with respect to axial distance for Pe =100 (for case (ii) ) |
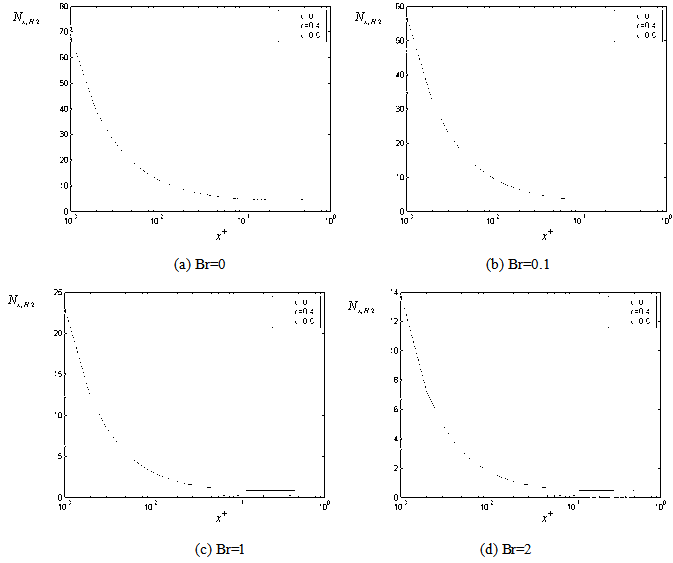 | Figure 9. The variation of the dimensionless local Nusselt number with respect to axial distance for Pe =10 (for case (ii) ) |
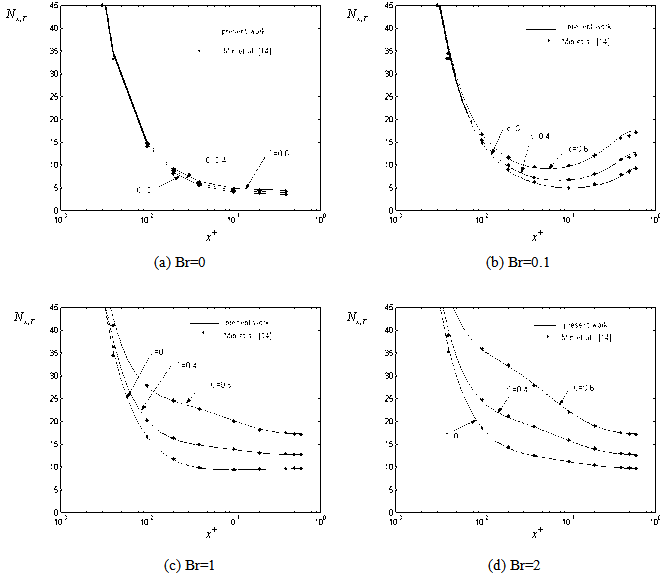 | Figure 10. Comparison of the local Nusselt number for case (i). for Pe= 10 |
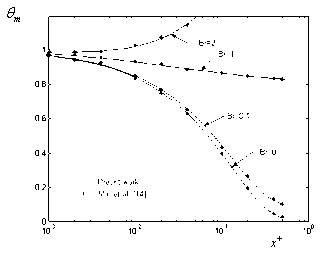 | Figure 11. Comparison of the mean temperature respect to axial distance for case (i) at c=0 and Pe = 10 |
5. Results and Discussion
Numerical results are presented in Figures (2 to 11). The results are made for Pe = 10, 100, with Br = 0, 0.1, 1, 2 and c = 0, 0.4, 0.6 over the range of 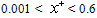 where the transverse mesh spacing
where the transverse mesh spacing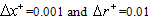 , for the two cases of the thermal boundary conditions. The variation of dimensionless mean temperature
, for the two cases of the thermal boundary conditions. The variation of dimensionless mean temperature with axial coordinate
with axial coordinate is shown for case(i) ( constant wall temperature ) in Figures 2(a , b , c ,d ) and 3(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature
is shown for case(i) ( constant wall temperature ) in Figures 2(a , b , c ,d ) and 3(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature 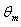 decreases with increasing the values of c (ratio of the yield shear stress to the wall shear stress) for the values of Br = 0, 0.1 and it increases with the increasing values of c for Br =1 , 2. The value of the dimensionless mean temperature
decreases with increasing the values of c (ratio of the yield shear stress to the wall shear stress) for the values of Br = 0, 0.1 and it increases with the increasing values of c for Br =1 , 2. The value of the dimensionless mean temperature 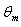 decreases with increasing the values of
decreases with increasing the values of 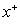 for values of Br = 0, 0.1 and it increases with increasing the values of
for values of Br = 0, 0.1 and it increases with increasing the values of 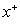 for Br =1 , 2. The value of the dimensionless mean temperature
for Br =1 , 2. The value of the dimensionless mean temperature 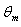 decreases with increasing the values of Peclet number Pe at the same value of Br and c .The variation of dimensionless mean temperature
decreases with increasing the values of Peclet number Pe at the same value of Br and c .The variation of dimensionless mean temperature 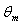 with axial coordinate
with axial coordinate 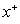 is shown for case(ii) ( constant wall heat flux) in Figures 4(a , b , c ,d ) and 5(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature
is shown for case(ii) ( constant wall heat flux) in Figures 4(a , b , c ,d ) and 5(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature 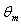 increases with increasing the values of c for the values of Br = 0.1 ,1 ,2 and it appears the same values with increasing values of c for Br =0. The value of the dimensionless mean temperature
increases with increasing the values of c for the values of Br = 0.1 ,1 ,2 and it appears the same values with increasing values of c for Br =0. The value of the dimensionless mean temperature 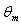 increases with increasing the values of
increases with increasing the values of 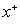 for all values of Br. The value of the dimensionless mean temperature
for all values of Br. The value of the dimensionless mean temperature 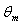 decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of the dimensionless mean temperature
decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of the dimensionless mean temperature 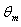 increases with increasing the values of Br for all values c and Pe.The variation of local Nusselt number
increases with increasing the values of Br for all values c and Pe.The variation of local Nusselt number 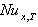 with axial coordinate
with axial coordinate 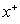 is shown for case(i) in Figures 6(a , b , c ,d ) and 7(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. It has been found that the value of local Nusselt number
is shown for case(i) in Figures 6(a , b , c ,d ) and 7(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. It has been found that the value of local Nusselt number 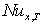 increases with increasing the values of c for all values of Br. The value of local Nusselt number
increases with increasing the values of c for all values of Br. The value of local Nusselt number 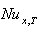 decreases with increasing the values of
decreases with increasing the values of 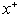 for all values of Br = 0 , 1, 2 and it decreases with increasing the values of
for all values of Br = 0 , 1, 2 and it decreases with increasing the values of 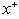 then it increases with increasing the values of
then it increases with increasing the values of 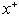 for the value of Br = 0.1 for the different value of Pe and c. It has been observed the local Nusselt number
for the value of Br = 0.1 for the different value of Pe and c. It has been observed the local Nusselt number 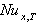 decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of local Nusselt number
decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of local Nusselt number 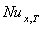 increases with increasing the values of Br for all values c and Pe. The variation of local Nusselt number
increases with increasing the values of Br for all values c and Pe. The variation of local Nusselt number 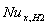 with axial coordinate
with axial coordinate 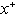 is shown for case(ii) in Figures 8(a , b , c ,d ) and 9(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of local Nusselt number
is shown for case(ii) in Figures 8(a , b , c ,d ) and 9(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of local Nusselt number 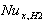 decreases with increasing the values of c for all values of Br = 0.1 , 1 ,2 but when Br = 0 it increases with increasing the values of c. Also it is observed that The value of local Nusselt number
decreases with increasing the values of c for all values of Br = 0.1 , 1 ,2 but when Br = 0 it increases with increasing the values of c. Also it is observed that The value of local Nusselt number 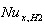 decreases with increasing the values of
decreases with increasing the values of 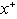 for all values of Br. Also it is observed that the value of local Nusselt number
for all values of Br. Also it is observed that the value of local Nusselt number 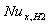 decreases with increasing the values of Peclet number Pe at the same value of Br and c. Also it is observed that The value of local Nusselt number
decreases with increasing the values of Peclet number Pe at the same value of Br and c. Also it is observed that The value of local Nusselt number 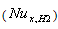 decreases with increasing the values of Br for all values c and Pe.Figure(10) shows the comparison of the local Nusselt number
decreases with increasing the values of Br for all values c and Pe.Figure(10) shows the comparison of the local Nusselt number 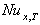 for case (i) with the results obtained by Min et al.[14]( c = 0, 0.4 , 0.6 ,Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[14]. Figure(11) shows the comparison of the mean temperature
for case (i) with the results obtained by Min et al.[14]( c = 0, 0.4 , 0.6 ,Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[14]. Figure(11) shows the comparison of the mean temperature 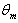 for case (i) with the results obtained by Min et al.[15] for c = 0 ( Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[15]. Tables (1) and (2) show the comparison of the mean temperature
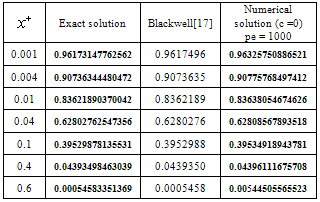
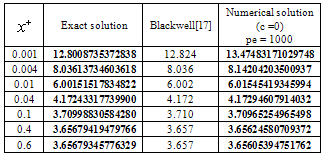
for case (i) with the results obtained by Min et al.[15] for c = 0 ( Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[15]. Tables (1) and (2) show the comparison of the mean temperature 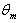 and the local Nusselt number
and the local Nusselt number 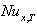 in the present work with previous work Blackwell[17] and exact solution for Newtonian fluid ( c= 0 , Br = 0 and Pe = 1000). It has been found that present results of this study are in good agreement with the results of Blackwell[17] and exact solution.
in the present work with previous work Blackwell[17] and exact solution for Newtonian fluid ( c= 0 , Br = 0 and Pe = 1000). It has been found that present results of this study are in good agreement with the results of Blackwell[17] and exact solution.Table 1. Comparison of the mean temperature in this work (numerical solution for c= 0 , Br=0 and Pe = 1000) with Blackwell[17] and Exact solution
 |
| |
|
Table 2. Comparison of the local Nusslt number in this work (numerical solution for c= 0 , Br=0 and Pe = 1000) with Blackwell[14] and Exact solution
 |
| |
|
6. Conclusions
A finite difference method has been used to numerically solve the energy equations for steady laminar fluid flow and heat transfer in entrance region of a circular pipe. A Bingham Non-Newtonian model is used to characterize the fluid behavior. Two cases of thermal boundary conditions (T and H2 ) are studied. Two-dimensional storage and marching technique with a relaxation method line by line solution procedure for the difference equations are some important features of the program. the effects of the Brinkman number ( Br = 0, 0.1 ,1 ,2 ), the thermal axial position 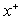 ,the Peclet number ( Pe = 100 , 10 ) and the ratio of the yield shear stress to the wall shear stress( c = 0,0.4 ,0.6) on the temperature
,the Peclet number ( Pe = 100 , 10 ) and the ratio of the yield shear stress to the wall shear stress( c = 0,0.4 ,0.6) on the temperature 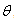 , the mean temperature
, the mean temperature  and the local Nusselt number
and the local Nusselt number 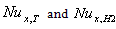 are studied. It is observed that,1- The value of the dimensionless mean temperature
are studied. It is observed that,1- The value of the dimensionless mean temperature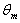 for case (i) decreases with increasing the values of
for case (i) decreases with increasing the values of  for values of Br = 0, 0.1 and it increases with increasing the values of
for values of Br = 0, 0.1 and it increases with increasing the values of 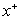 for Br =1 , 2. Also the value of the dimensionless mean temperature
for Br =1 , 2. Also the value of the dimensionless mean temperature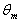 decreases with increasing the values of Peclet number Pe .2- The value of the dimensionless mean temperature
decreases with increasing the values of Peclet number Pe .2- The value of the dimensionless mean temperature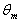 for case (ii) increases with increasing the values of for all values of Br . Also the value of the dimensionless mean temperature(
for case (ii) increases with increasing the values of for all values of Br . Also the value of the dimensionless mean temperature(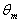 ) decreases with increasing the values of Peclet number Pe and it increases with increasing of the Br .3- The value of local Nusselt number
) decreases with increasing the values of Peclet number Pe and it increases with increasing of the Br .3- The value of local Nusselt number 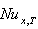 for case(i) decreases with increasing the values of
for case(i) decreases with increasing the values of 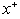 for all values of Br .Also the value of local Nusselt number
for all values of Br .Also the value of local Nusselt number 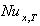 decreases with increasing the values of Peclet number Pe , while increases with increasing the values of Br .4- The value of local Nusselt number
decreases with increasing the values of Peclet number Pe , while increases with increasing the values of Br .4- The value of local Nusselt number 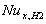 for case (ii) decreases with increasing the values of
for case (ii) decreases with increasing the values of 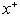 for all values of Br , and it decreases with increasing the values of Peclet number Pe . Also it is observed that The value of local Nusselt number
for all values of Br , and it decreases with increasing the values of Peclet number Pe . Also it is observed that The value of local Nusselt number 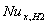 decreases with increasing the values of Br .
decreases with increasing the values of Br .
References
| [1] | Shah, R. K. and London, A. L., Laminar flow forced convection in ducts. Advances in Heat Transfer (suppl.1). Academic Press, New York, 1978. |
| [2] | Tyagi V.P., Laminar forced convection of a dissipative fluid in a channel. J Heat Transfer 1996;88:161–169. |
| [3] | Ou J.W. and Cheng K.C. ,Viscous dissipation effects in the entrance region heat transfer in pipes with uniform heat flux. Appl Sci Res 1973;28:289–301. |
| [4] | Lin T.F., Hawks K.H. and Leidenfrost W., Analysis of viscous dissipation effect on the thermal entrance heat transfer in laminar pipe flows with convective boundary conditions, Warm Stoffubertrag 1983;17: 97–105. |
| [5] | Basu T and Roy D.N., Laminar heat transfer in a tube with viscous dissipation, Int J Heat Mass Transfer 1985;28:699–701. |
| [6] | Zanchini E., Effect of viscous dissipation on the asymptotic behavior of laminar forced convection in circular tubes, Int J Heat Mass Transfer 1997;40:169–178. |
| [7] | Aydin O., Effects of viscous dissipation on the heat transfer in a forced Thermally developing flow, Energy Conversion and Management 2005;46: 3091–3102. |
| [8] | Liou C.T. and Wang F.S. ,Solutions to the extended Graetz problem for a power-law fluid with viscous dissipation and different entrance boundary conditions, Numer Heat Transfer A 1990;17:91–108. |
| [9] | Berardi P.G. , Cuccurullo G. , Acierno D. and Russo P. ,Viscous dissipation in duct flow of molten polymers, In: Proceedings of Eurotherm Seminar 46, Pisa, Italy; July 1995. p. 39–43. |
| [10] | Lawal A.and Mujumdar A.S., The effects of viscous dissipation on heat transfer to power law fluids in arbitrary cross sectional ducts, Warm Stoffubertrag 1992;27:437–46. |
| [11] | Dang V.D., Heat transfer of a power-law fluid at low Peclet number flow, J Heat Transfer 1983;105:542–9. |
| [12] | Barletta A., Fully developed laminar forced convection in circular ducts for power-law fluids with viscous dissipation , Int J Heat Mass Transfer 1997;40(1):15–26. |
| [13] | Valko, P.P., Solution of the Graetz–Brinkman problem with the Laplace transform Galerkin method, International Journal of Heat and Mass Transfer 2005;48: 1874–1882. |
| [14] | Khatyr R., Ouldhadda D. and Il Idrissi A., Viscous dissipation effects on the asymptotic behavior of laminar forced convection for Bingham plastics in circular ducts , Int J Heat Mass Transfer 2003;46:589–98. |
| [15] | Min T., Yoo J.Y. and Choi H., Laminar convective heat transfer of a Bingham plastic in a circular pipe––I. Analytical approach––thermally fully developed flow and thermally developing flow (the Graetz problem extended), Int J Heat Mass Transfer 1997;40:3025–3037. |
| [16] | Jain M.K. , Lyenger S.R.K ., and Jain R.K. , Numerical Method for Scientific and Engineering Computation , Wiely Eastern Limited New Delhi, second edition,1991. |
| [17] | Blackwell, B. F., Numerical solution of the Graetz problem for a Bingham plastic in laminar tube flow with constant wall temperature, Journal of Heat Transfer, 1985; 107:466-468. |


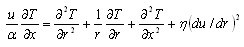
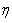 is the apparent viscosity for a Bingham model and given by
is the apparent viscosity for a Bingham model and given by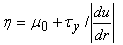
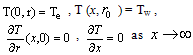
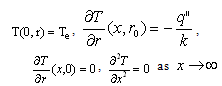
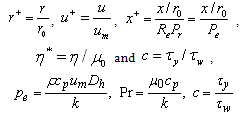 Where r0 is the radius of the tube, τw is the wall shear stress and Dh is the hydraulic diameter.The energy equation (1) is written in the following non-dimensional form by Min et al.[14] as
Where r0 is the radius of the tube, τw is the wall shear stress and Dh is the hydraulic diameter.The energy equation (1) is written in the following non-dimensional form by Min et al.[14] as 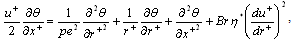

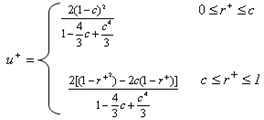
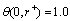 ,
, 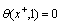 ,
, 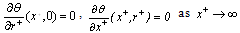
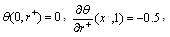
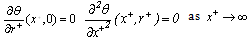
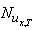 ,
, 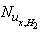 according to the two cases of the thermal boundary conditions are given by
according to the two cases of the thermal boundary conditions are given by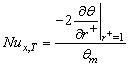
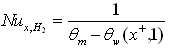
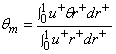
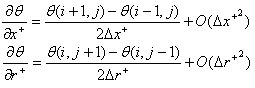 The finite-difference form of the energy equation (5) is:
The finite-difference form of the energy equation (5) is: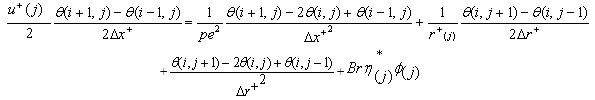
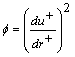 Rearranging equation (13) in the form as:
Rearranging equation (13) in the form as: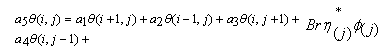
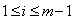 ,
,  where ,
where , 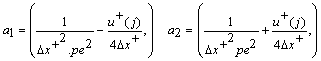
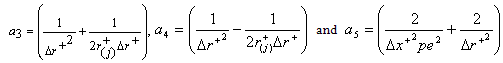 For
For 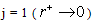 the term
the term 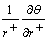 is undefined, therefore we apply the L’Hopital’s rule. Then
is undefined, therefore we apply the L’Hopital’s rule. Then 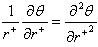 In the equation (13) becomes;
In the equation (13) becomes;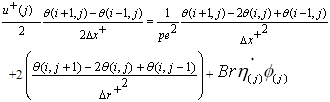
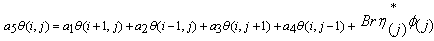
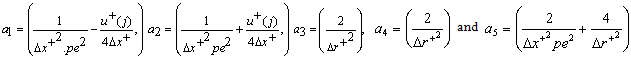 The difference forms of the boundary conditions are:For case (i):
The difference forms of the boundary conditions are:For case (i): 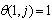
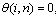
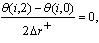
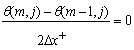 For case (ii):
For case (ii): 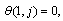
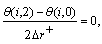
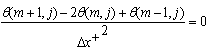 To compute Nusselt number and mean temperature for two cases of temperature boundary conditions we may introduce finite-difference forms for the integrals and the first partial derivatives in equations (10) and (12) .The Simpson rule for single integral is introduced by Jain et al.[16], is used to introduce a difference form for the integral equation (11) as
To compute Nusselt number and mean temperature for two cases of temperature boundary conditions we may introduce finite-difference forms for the integrals and the first partial derivatives in equations (10) and (12) .The Simpson rule for single integral is introduced by Jain et al.[16], is used to introduce a difference form for the integral equation (11) as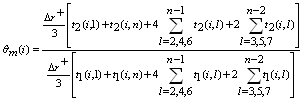 Where,
Where, 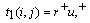
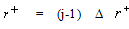 ,
, 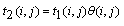
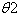 as unknown variable notation), in the first we get the velocity from equation (7), and the energy equation (14) is then solved to obtain
as unknown variable notation), in the first we get the velocity from equation (7), and the energy equation (14) is then solved to obtain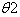 .The linear algebraic equations resulting from equation (14) may be written in the matrix form as
.The linear algebraic equations resulting from equation (14) may be written in the matrix form as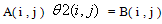
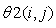 : Designate the unknowns in the algebraic equationsB( i , j ) : Designate the residual in the algebraic equationsi = 1,2,3,…………,n and j=1,2,3,…………,mThe relaxation equation can be written in the form of :
: Designate the unknowns in the algebraic equationsB( i , j ) : Designate the residual in the algebraic equationsi = 1,2,3,…………,n and j=1,2,3,…………,mThe relaxation equation can be written in the form of :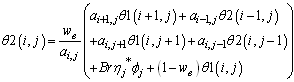
 : Known values of the temperature in the old iterations,
: Known values of the temperature in the old iterations,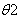 : Unknown values of the temperature in the new iterations,
: Unknown values of the temperature in the new iterations,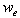 : Relaxation factor,a: the coefficient of
: Relaxation factor,a: the coefficient of  .The resulting of a linear algebraic system of equations are solved by using successive over relaxation method (S.O.R) with relaxation factor
.The resulting of a linear algebraic system of equations are solved by using successive over relaxation method (S.O.R) with relaxation factor 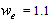 . The process repeated up till the difference between the new and old temperature value at each point is less than
. The process repeated up till the difference between the new and old temperature value at each point is less than 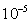 .
.









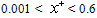 where the transverse mesh spacing
where the transverse mesh spacing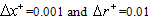 , for the two cases of the thermal boundary conditions. The variation of dimensionless mean temperature
, for the two cases of the thermal boundary conditions. The variation of dimensionless mean temperature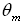 with axial coordinate
with axial coordinate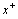 is shown for case(i) ( constant wall temperature ) in Figures 2(a , b , c ,d ) and 3(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature
is shown for case(i) ( constant wall temperature ) in Figures 2(a , b , c ,d ) and 3(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature 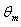 decreases with increasing the values of c (ratio of the yield shear stress to the wall shear stress) for the values of Br = 0, 0.1 and it increases with the increasing values of c for Br =1 , 2. The value of the dimensionless mean temperature
decreases with increasing the values of c (ratio of the yield shear stress to the wall shear stress) for the values of Br = 0, 0.1 and it increases with the increasing values of c for Br =1 , 2. The value of the dimensionless mean temperature 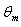 decreases with increasing the values of
decreases with increasing the values of 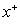 for values of Br = 0, 0.1 and it increases with increasing the values of
for values of Br = 0, 0.1 and it increases with increasing the values of 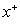 for Br =1 , 2. The value of the dimensionless mean temperature
for Br =1 , 2. The value of the dimensionless mean temperature 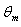 decreases with increasing the values of Peclet number Pe at the same value of Br and c .The variation of dimensionless mean temperature
decreases with increasing the values of Peclet number Pe at the same value of Br and c .The variation of dimensionless mean temperature 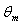 with axial coordinate
with axial coordinate 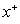 is shown for case(ii) ( constant wall heat flux) in Figures 4(a , b , c ,d ) and 5(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature
is shown for case(ii) ( constant wall heat flux) in Figures 4(a , b , c ,d ) and 5(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of the dimensionless mean temperature 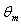 increases with increasing the values of c for the values of Br = 0.1 ,1 ,2 and it appears the same values with increasing values of c for Br =0. The value of the dimensionless mean temperature
increases with increasing the values of c for the values of Br = 0.1 ,1 ,2 and it appears the same values with increasing values of c for Br =0. The value of the dimensionless mean temperature 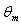 increases with increasing the values of
increases with increasing the values of 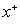 for all values of Br. The value of the dimensionless mean temperature
for all values of Br. The value of the dimensionless mean temperature 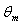 decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of the dimensionless mean temperature
decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of the dimensionless mean temperature 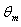 increases with increasing the values of Br for all values c and Pe.The variation of local Nusselt number
increases with increasing the values of Br for all values c and Pe.The variation of local Nusselt number 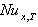 with axial coordinate
with axial coordinate 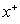 is shown for case(i) in Figures 6(a , b , c ,d ) and 7(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. It has been found that the value of local Nusselt number
is shown for case(i) in Figures 6(a , b , c ,d ) and 7(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. It has been found that the value of local Nusselt number 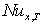 increases with increasing the values of c for all values of Br. The value of local Nusselt number
increases with increasing the values of c for all values of Br. The value of local Nusselt number 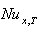 decreases with increasing the values of
decreases with increasing the values of 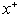 for all values of Br = 0 , 1, 2 and it decreases with increasing the values of
for all values of Br = 0 , 1, 2 and it decreases with increasing the values of 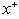 then it increases with increasing the values of
then it increases with increasing the values of 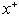 for the value of Br = 0.1 for the different value of Pe and c. It has been observed the local Nusselt number
for the value of Br = 0.1 for the different value of Pe and c. It has been observed the local Nusselt number 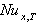 decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of local Nusselt number
decreases with increasing the values of Peclet number Pe at the same value of Br and c. The value of local Nusselt number 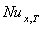 increases with increasing the values of Br for all values c and Pe. The variation of local Nusselt number
increases with increasing the values of Br for all values c and Pe. The variation of local Nusselt number 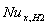 with axial coordinate
with axial coordinate 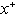 is shown for case(ii) in Figures 8(a , b , c ,d ) and 9(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of local Nusselt number
is shown for case(ii) in Figures 8(a , b , c ,d ) and 9(a , b , c ,d ) for Peclet numbers, Pe = 100,10, respectively and different Brinkman number Br = 0, 0.1 , 1 ,2. The study of this Figures shows that the value of local Nusselt number 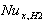 decreases with increasing the values of c for all values of Br = 0.1 , 1 ,2 but when Br = 0 it increases with increasing the values of c. Also it is observed that The value of local Nusselt number
decreases with increasing the values of c for all values of Br = 0.1 , 1 ,2 but when Br = 0 it increases with increasing the values of c. Also it is observed that The value of local Nusselt number 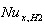 decreases with increasing the values of
decreases with increasing the values of 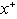 for all values of Br. Also it is observed that the value of local Nusselt number
for all values of Br. Also it is observed that the value of local Nusselt number 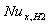 decreases with increasing the values of Peclet number Pe at the same value of Br and c. Also it is observed that The value of local Nusselt number
decreases with increasing the values of Peclet number Pe at the same value of Br and c. Also it is observed that The value of local Nusselt number 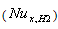 decreases with increasing the values of Br for all values c and Pe.Figure(10) shows the comparison of the local Nusselt number
decreases with increasing the values of Br for all values c and Pe.Figure(10) shows the comparison of the local Nusselt number 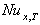 for case (i) with the results obtained by Min et al.[14]( c = 0, 0.4 , 0.6 ,Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[14]. Figure(11) shows the comparison of the mean temperature
for case (i) with the results obtained by Min et al.[14]( c = 0, 0.4 , 0.6 ,Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[14]. Figure(11) shows the comparison of the mean temperature 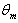 for case (i) with the results obtained by Min et al.[15] for c = 0 ( Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[15]. Tables (1) and (2) show the comparison of the mean temperature
for case (i) with the results obtained by Min et al.[15] for c = 0 ( Br = 0 , 0.1 ,1 ,2 and Pe =10 ). It has been found that present results of this study are in good agreement with the results of Min et al.[15]. Tables (1) and (2) show the comparison of the mean temperature 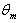 and the local Nusselt number
and the local Nusselt number 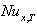 in the present work with previous work Blackwell[17] and exact solution for Newtonian fluid ( c= 0 , Br = 0 and Pe = 1000). It has been found that present results of this study are in good agreement with the results of Blackwell[17] and exact solution.
in the present work with previous work Blackwell[17] and exact solution for Newtonian fluid ( c= 0 , Br = 0 and Pe = 1000). It has been found that present results of this study are in good agreement with the results of Blackwell[17] and exact solution.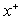 ,the Peclet number ( Pe = 100 , 10 ) and the ratio of the yield shear stress to the wall shear stress( c = 0,0.4 ,0.6) on the temperature
,the Peclet number ( Pe = 100 , 10 ) and the ratio of the yield shear stress to the wall shear stress( c = 0,0.4 ,0.6) on the temperature 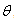 , the mean temperature
, the mean temperature  and the local Nusselt number
and the local Nusselt number 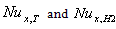 are studied. It is observed that,1- The value of the dimensionless mean temperature
are studied. It is observed that,1- The value of the dimensionless mean temperature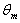 for case (i) decreases with increasing the values of
for case (i) decreases with increasing the values of  for values of Br = 0, 0.1 and it increases with increasing the values of
for values of Br = 0, 0.1 and it increases with increasing the values of 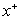 for Br =1 , 2. Also the value of the dimensionless mean temperature
for Br =1 , 2. Also the value of the dimensionless mean temperature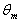 decreases with increasing the values of Peclet number Pe .2- The value of the dimensionless mean temperature
decreases with increasing the values of Peclet number Pe .2- The value of the dimensionless mean temperature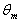 for case (ii) increases with increasing the values of for all values of Br . Also the value of the dimensionless mean temperature(
for case (ii) increases with increasing the values of for all values of Br . Also the value of the dimensionless mean temperature(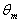 ) decreases with increasing the values of Peclet number Pe and it increases with increasing of the Br .3- The value of local Nusselt number
) decreases with increasing the values of Peclet number Pe and it increases with increasing of the Br .3- The value of local Nusselt number 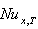 for case(i) decreases with increasing the values of
for case(i) decreases with increasing the values of 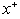 for all values of Br .Also the value of local Nusselt number
for all values of Br .Also the value of local Nusselt number 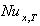 decreases with increasing the values of Peclet number Pe , while increases with increasing the values of Br .4- The value of local Nusselt number
decreases with increasing the values of Peclet number Pe , while increases with increasing the values of Br .4- The value of local Nusselt number 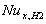 for case (ii) decreases with increasing the values of
for case (ii) decreases with increasing the values of 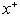 for all values of Br , and it decreases with increasing the values of Peclet number Pe . Also it is observed that The value of local Nusselt number
for all values of Br , and it decreases with increasing the values of Peclet number Pe . Also it is observed that The value of local Nusselt number 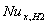 decreases with increasing the values of Br .
decreases with increasing the values of Br . Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
