Joanna Ammerlaan, Tzvetalin S. Vassilev
Department of Mathematics and Computer Science, Nipissing University, North Bay, Canada
Correspondence to: Tzvetalin S. Vassilev, Department of Mathematics and Computer Science, Nipissing University, North Bay, Canada.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper takes a look at various properties of binary hypercubes and middle level graphs, a particular subgraph of the binary hypercube. The intention is to shed some light on the middle level conjecture by discovering patterns within the subgraphs and the known Hamiltonian cycles for those graphs. The problem is closely related to determining Hamiltonicity of graphs and is also closely tied to Gray code cycles and binary sequences.
Keywords:
Middle Level Conjecture, Hypercubes, Hamiltonicity, Queue Gray Code
Cite this paper: Joanna Ammerlaan, Tzvetalin S. Vassilev, Properties of the Binary Hypercube and Middle Level Graphs, Applied Mathematics, Vol. 3 No. 1, 2013, pp. 20-26. doi: 10.5923/j.am.20130301.03.
1. Introduction
A hypercube, sometimes referred to as a n-cube, is the graphical representation of the edges and vertices in a single volumetric unit in any dimension n. It is well known that these graphs are Hamiltonian. The question of whether particular subgraphs of the hypercube are Hamiltonian is less clear.First proposed in the 1980’s by Ivan Havel, the Middle Level Conjecture, under the name “The Revolving Door Conjecture”[1] remains an open problem in mathematics unanimously thought to be true. The conjecture states that for every odd n-dimensional hypercube for 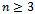 , there exists a Hamiltonian cycle in the graph of the middle layers of the hypercube. The difficulty in solving the problem is undoubtedly due in part to the unclear nature of Hamiltonian cycles in general, for there is no known method to prove the existence of a Hamiltonian cycle in a graph. There are a few strategies which can be used to disprove the existence of such cycles [2], but the middle level graph, as little effort will show, fails on these accounts. As of 2006, with the aid of technology,
, there exists a Hamiltonian cycle in the graph of the middle layers of the hypercube. The difficulty in solving the problem is undoubtedly due in part to the unclear nature of Hamiltonian cycles in general, for there is no known method to prove the existence of a Hamiltonian cycle in a graph. There are a few strategies which can be used to disprove the existence of such cycles [2], but the middle level graph, as little effort will show, fails on these accounts. As of 2006, with the aid of technology, 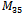 and
and 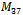 were the largest graphs of this nature to be proved to contain Hamiltonian cycles [5, 9]. This paper takes a look at various properties of the hypercube and the middle level graph as well as the use of Gray codes to develop some of these properties. Finally, this paper will look into how queue Gray codes can be used to search for paths and cycles within middle level graphs and the results of queue Gray code and antipodal tests on known Hamiltonian paths within various middle level graphs.
were the largest graphs of this nature to be proved to contain Hamiltonian cycles [5, 9]. This paper takes a look at various properties of the hypercube and the middle level graph as well as the use of Gray codes to develop some of these properties. Finally, this paper will look into how queue Gray codes can be used to search for paths and cycles within middle level graphs and the results of queue Gray code and antipodal tests on known Hamiltonian paths within various middle level graphs.
2. Definitions and Notations
Definition 1 (Hypercube)A hypercube is the graphical representation of the edges and vertices in a single volumetric unit in any dimension n. For the purpose of this paper it should be noted that all hypercubes refer to binary n-dimensional graphs. These graphs are denoted by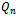 , where n is the dimension (Fig. 1).
, where n is the dimension (Fig. 1).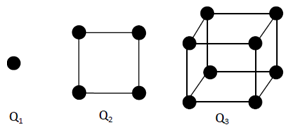 | Figure 1. Hypercubes of the first, second and third dimension |
Definition 2 (Hamiltonian Path)In a graph 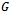 a path that contains every vertex of
a path that contains every vertex of 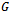 once is referred to as a Hamiltonian Path [2].Definition 3 (Hamiltonian Cycle)In a graph
once is referred to as a Hamiltonian Path [2].Definition 3 (Hamiltonian Cycle)In a graph 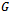 , a cycle c of
, a cycle c of 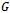 , which contains every vertex of
, which contains every vertex of 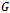 once, is said to be a Hamiltonian cycle, and for this reason,
once, is said to be a Hamiltonian cycle, and for this reason, 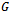 is called a Hamiltonian graph[2].Definition 4 (Vertex Levels of a Hypercube)When mapped to a coordinate axis, each vertex of a hypercube,
is called a Hamiltonian graph[2].Definition 4 (Vertex Levels of a Hypercube)When mapped to a coordinate axis, each vertex of a hypercube, 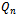 , can be assigned a binary string of length n. The
, can be assigned a binary string of length n. The 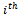 level of the hypercube refers to the set of vertices of
level of the hypercube refers to the set of vertices of 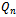 which contain I ones in their vertex string (Fig. 2).Definition 5 (Middle Level Graph)The middle layer graph, denoted
which contain I ones in their vertex string (Fig. 2).Definition 5 (Middle Level Graph)The middle layer graph, denoted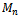 , is a subgraph of
, is a subgraph of 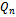 containing the vertices in levels
containing the vertices in levels 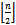 and
and 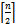 (Fig. 2).Definition 6 (Word or String)The terms word and string are used interchangeably to refer to a binary number consisting of a sequence of zeros and ones.
(Fig. 2).Definition 6 (Word or String)The terms word and string are used interchangeably to refer to a binary number consisting of a sequence of zeros and ones.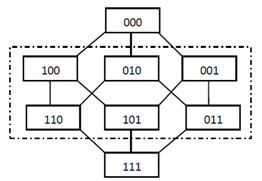 | Figure 2. A layered Q3 graph with M3 outlined in the center |
3. Gray Code
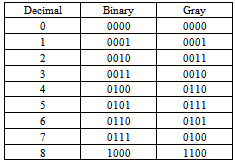
Tightly coupled with the notion of binary counting is that of Gray Code. Gray code is a binary counting system in which consecutive numbers differ by a single bit. Where the binary counting system, like the decimal counting system, places the value of a bit or number on the digit’s position, Gray code does not. Rather, Gray code is produced by applying the exclusive-or operation to consecutive bits of the equivalent binary number (Table. 1)[3].Table 1. Decimal Binary Gray Comparison
 |
| |
|
3.1. Cyclic Gray Code
A finite Gray code sequence is called cyclic if the transition between the last word of the sequence and the first is a single bit exchange; that is the first and last strings differ by a single binary digit. Thus, a Gray code cycle consisting of words of length n contains all the 2n possible bit string combinations [4].Cyclic Gray code can be inductively produced through reflected binary code. The trivial case is when words have a length of one. Clearly, the two words in the Gray code sequence form a cycle. If the word length n, is two, a cyclic Gray code can be produced by concatenating the cycle for 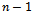 , and its reflection and appending a zero bit to the left side of the unreflected words and a one bit to the left of the reflected words (Fig. 3). The result is a sequence of 2n words of length n where the first and the last differ by a single bit. Continuing, in this manner inductively, a cyclic Gray code sequence can be produced for all words of length n.
, and its reflection and appending a zero bit to the left side of the unreflected words and a one bit to the left of the reflected words (Fig. 3). The result is a sequence of 2n words of length n where the first and the last differ by a single bit. Continuing, in this manner inductively, a cyclic Gray code sequence can be produced for all words of length n. | Figure 3. Recursive construction of Gray Codes for  |
3.2. Queue Gray Code
Queue Gray code adds an additional constraint to that of standard Gray code. In a queue Gray code every consecutive word is produced from the previous by removing the most significant bit, shifting the remaining bits one position to the left, and appending a new least significant bit (Fig. 4). Figure 6 shows several examples of queue Gray code sequences. It becomes clear then, that particular substrings become illegal in queue Gray code.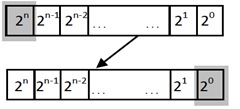 | Figure 4. Queue Gray Code Bit Shift between Consecutive Words |
Consider the substring ‘101’ of a word. Shifting these bits one digit to the left will create a consecutive queue Gray code word which differs from the previous by at least two bits. This however, breaks the most basic law for Gray code. Thus, no word which contains the substring ‘101’ can produce a consecutive queue Gray code word. Similarly, it can be shown that the substring ‘010’ is also illegal. Further, it is impossible to legally create either illegal substring. In order to create a word containing one, the previous consecutive word must have the two least significant bits differ; ’01’ or ’10’. To create the illegal form, both these bit must change. Again, this violates Gray code. It follows then that no queue Gray code sequence containing words of length greater than three will contain any word containing either substring ‘010’ or ‘101’.It can similarly be shown that ‘1001’, ‘0110’, and any substring which does not partition the 1s and 0s to the left and right side of the word is illegal.Proof Here we prove the case when the first and last bits are 1 and there exists at least one 0 bit in the middle. The proof for the opposite case is similar.Suppose a word contains a substring as described above. Let the zero bit be the 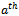 bit in the string. The first ones bit immediately to left of
bit in the string. The first ones bit immediately to left of 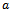 in the
in the 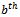 bit of the substring, and the first ones bit immediately to the right of
bit of the substring, and the first ones bit immediately to the right of 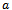 be in the
be in the 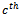 bit of the substring.In the next consecutive word, all the bits of the substring will be shifted one bit to the left. Consider this new word. In the
bit of the substring.In the next consecutive word, all the bits of the substring will be shifted one bit to the left. Consider this new word. In the 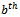 position there will be a zero and in the
position there will be a zero and in the 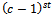 position there will be a one. Since the previous consecutive word contained a one and a zero respectively in these positions, two bits have changed between words (Fig. 5). Thus, the shift is not a Gray code shift: a contradiction.
position there will be a one. Since the previous consecutive word contained a one and a zero respectively in these positions, two bits have changed between words (Fig. 5). Thus, the shift is not a Gray code shift: a contradiction.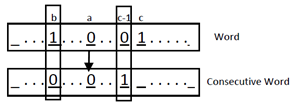 | Figure 5. Queue Gray Code Illegal Substring Form |
From the illegal substrings it follows that every word in a queue Gray code sequence must have the zeros and ones partitioned; that is all the zeros are on the left side of the word and the ones on the right or vice versa. This gives an upper bound of 2n. A queue Gary code sequence, in fact a cycle, can systematically be generated (Fig. 6). From here it is clear that 2n is an exact upper bound for the length of a queue Gray code path.
4. Properties of the Hypercube
Given that the hypercube represents a single volumetric unit in any dimension, it follows that the length of each edge is 1 unit and that all edges which meet at a vertex are perpendicular to each other. It also follows that each vertex can be assigned a unique binary string of length n if the hypercube is placed at the origin of the coordinate systems. Each vertex string corresponds to the coordinate location of the vertex resulting in a unique binary word. The number of vertices is equivalent to the number of possible binary strings of length 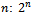 . The degree of each vertex is the dimension n and adjacent vertices differ by a single bit.
. The degree of each vertex is the dimension n and adjacent vertices differ by a single bit.
4.1. A Layered Graph
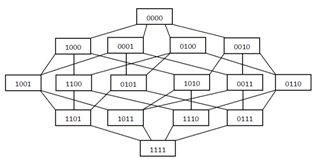
It is helpful to construct the graph of a hypercube as a layered structure. Specifically, the vertices can be grouped based on the number of ones which appear in their corresponding string; the 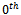 layer containing no ones and the
layer containing no ones and the 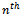 layer containing only ones (Fig. 7).It is apparent that edges only exist between consecutive vertex layers of the graph and not between edges of the same layer. This follows from the fact that edges only exist between vertices which differ by one bit; that is, one endpoint of an edge will contain one more one than the other. Thus, the layered graph will only contain edges between consecutive layers. It is readily apparent then that the graph of a hypercube is also bipartite.
layer containing only ones (Fig. 7).It is apparent that edges only exist between consecutive vertex layers of the graph and not between edges of the same layer. This follows from the fact that edges only exist between vertices which differ by one bit; that is, one endpoint of an edge will contain one more one than the other. Thus, the layered graph will only contain edges between consecutive layers. It is readily apparent then that the graph of a hypercube is also bipartite.  | Figure 6. Queue Gray Code Cycles |
The number of vertices in each layer is simply a combination of the number of ones and the dimension of the graph. The 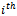 vertex layer of a hypercube contains
vertex layer of a hypercube contains 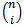 vertices and between vertex layers
vertices and between vertex layers 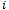 and
and 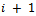 there exists an edge layer containing
there exists an edge layer containing 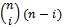 or equivalently
or equivalently 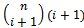 edges.
edges.
4.2. Hamiltonicity of Hypercubes
 | Figure 7. Layered Hypercube Graph of Q4 |
A Hamiltonian path can easily be found in a Hypercube 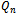 by considering the Gray code sequence of length n. Beginning at the origin, the vertex whose word is a string of n zeros, each consecutive vertex in the path is simply the consecutive Gray code word. These vertices will be adjacent because their binary strings differ by a single bit (as per the definition of Gray code). Since a Gray code sequence will exist through all
by considering the Gray code sequence of length n. Beginning at the origin, the vertex whose word is a string of n zeros, each consecutive vertex in the path is simply the consecutive Gray code word. These vertices will be adjacent because their binary strings differ by a single bit (as per the definition of Gray code). Since a Gray code sequence will exist through all 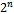 possible strings, it follows that a Hamiltonian path will exists.It can similarly be shown that the hypercube is Hamiltonian. In this case we simply consider the reflected Gray code sequences. Again, because this cyclic sequence exists and is of length
possible strings, it follows that a Hamiltonian path will exists.It can similarly be shown that the hypercube is Hamiltonian. In this case we simply consider the reflected Gray code sequences. Again, because this cyclic sequence exists and is of length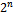 , a Hamiltonian cycle will exist in
, a Hamiltonian cycle will exist in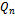 .
.
5. The Middle Level (Layer) Graph
The middle level graph 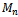 is a subgraph of
is a subgraph of 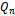 containing those vertices in levels
containing those vertices in levels 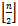 and
and 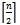 and the edges between them. When n is even however,
and the edges between them. When n is even however, 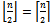 and the subgraph contains only vertices on a single middle layer. Since no edges exist between vertices in the same vertex layer, each vertex will have a degree of zero and the graph will be completely disconnected. No Hamiltonian path or cycle could possibly exist. When n is odd, Hamiltonicity is less clear.
and the subgraph contains only vertices on a single middle layer. Since no edges exist between vertices in the same vertex layer, each vertex will have a degree of zero and the graph will be completely disconnected. No Hamiltonian path or cycle could possibly exist. When n is odd, Hamiltonicity is less clear.
5.1. The Middle Level Conjecture
As there is not too much to be said about the middle layer graphs when n is even, the Middle Level Conjecture considers only graphs where the dimension is odd. As previously stated, the Middle Level Conjecture says that for every odd 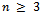 ,
, 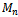 is Hamiltonian.When
is Hamiltonian.When 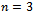 , the only Hamiltonian cycle in
, the only Hamiltonian cycle in 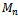 is rather trivial as it is also an Euler path and the total number of edges is only 6 (middle level of Fig. 2). It is considerably more difficult to locate a Hamiltonian cycle in
is rather trivial as it is also an Euler path and the total number of edges is only 6 (middle level of Fig. 2). It is considerably more difficult to locate a Hamiltonian cycle in 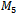 , despite the fact that the graph contains several such cycles (Fig. 9).
, despite the fact that the graph contains several such cycles (Fig. 9).
5.2. Edge Colouring
An approach proposed by Parkhomenko for classifying the Hamiltonian cycles in hypercubes is to classify the edges of the graph rather than to simply focus on the vertices[6]. What he proposed was to assign a weight to each of the edges based upon the axis it was parallel to. In terms of the binary string, this would be assigning a weight to an edge based on the position of the bit which changes over the edge. The weight of an edge joining two adjacent vertices which differ in the 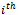 bit, is equivalent to the weight of the
bit, is equivalent to the weight of the 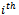 position in the string.
position in the string. 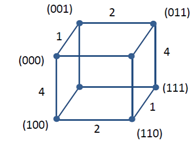 | Figure 8. Edge Weights in Q3 |
For example, consider that graph of a standard cube (Fig. 8). The number of axes is equal to the dimension of the cube and the length if each of the vertex words; in this case three. The x-axis is represented by the first bit in the string, the y-axis the second, and the z-axis the third. An edge that represents a change in the first bit will be parallel to the x-axis and have a weight of 22. Similarly the y-axis parallel edges have a weight of 21 and the z-axis 20. Each of the different weights can be assigned a unique colour. What is more, in the case of 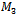 the Hamiltonian path is a sequence of alternating colours
the Hamiltonian path is a sequence of alternating colours 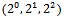 and the graph contains the same number of edges of each colour. This is also the case with
and the graph contains the same number of edges of each colour. This is also the case with 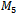 . Though there does not appear to be a clear pattern between the edge colours in the Hamiltonian cycles, there remains four edges of each colour in the cycles.
. Though there does not appear to be a clear pattern between the edge colours in the Hamiltonian cycles, there remains four edges of each colour in the cycles.
5.3. Proposition 1
Each edge level of 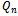 contains an equal number of edges of each colour.Proof (Please refer to Fig. 7)Let
contains an equal number of edges of each colour.Proof (Please refer to Fig. 7)Let 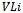 refer to vertex level i and
refer to vertex level i and 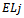 refer to edge level j which resides between
refer to edge level j which resides between 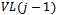 and
and 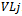 . Each of the j ones in
. Each of the j ones in 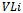 will refer to an edge in
will refer to an edge in 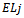 and following the edge to
and following the edge to 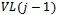 will result in a string missing one of the ones. Recall the position of the missing one determines the colour of the edge. We also know that each vertex will contain an edge of every colour, each corresponding to the axis represented by the changing bit.Beginning with
will result in a string missing one of the ones. Recall the position of the missing one determines the colour of the edge. We also know that each vertex will contain an edge of every colour, each corresponding to the axis represented by the changing bit.Beginning with 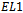 ,
, 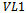 contains exactly
contains exactly 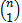 vertices representing each of the n possible positions of the ones bit in the word. It follows then that
vertices representing each of the n possible positions of the ones bit in the word. It follows then that  contains a single edge of each colour.
contains a single edge of each colour.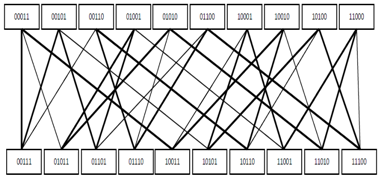 | Figure 9. Hamiltonian Path in M5 |
Moving down to 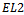 ,
, 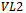 contains exactly
contains exactly  combinations of positions for the two ones in the words. Each of the
combinations of positions for the two ones in the words. Each of the 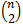 vertices will be adjacent to a pair of uniquely coloured edges in
vertices will be adjacent to a pair of uniquely coloured edges in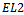 . By fixing one colour and choosing another from the remaining
. By fixing one colour and choosing another from the remaining 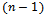 we get that there are
we get that there are 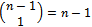 edges of each colour. Looking up to
edges of each colour. Looking up to 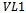 it can be seen that an edge of each colour extends down from each of the vertices to a vertex in
it can be seen that an edge of each colour extends down from each of the vertices to a vertex in 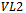 except for the vertex in
except for the vertex in 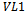 which is adjacent to
which is adjacent to 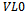 by an edge of that colour. The total number of edges in
by an edge of that colour. The total number of edges in 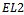 is confirmed by multiplying the number of vertices in
is confirmed by multiplying the number of vertices in 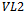 by their degree in
by their degree in 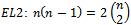 .Similarly,
.Similarly, 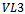 contains
contains 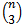 different vertices each containing a unique set of three coloured edges in
different vertices each containing a unique set of three coloured edges in 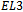 ,
, 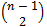 edges of each colour exist in
edges of each colour exist in 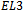 , and the total number of edges in
, and the total number of edges in 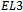 is equal to the product of number of edges of each colour and the number of colours:
is equal to the product of number of edges of each colour and the number of colours: 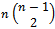 . The number of edges of each colour in
. The number of edges of each colour in 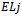 is
is 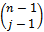 . Therefore, there are an equal number of edges of each colour in each of the edge layers.
. Therefore, there are an equal number of edges of each colour in each of the edge layers.
5.4. Proposition 2
Each Hamiltonian cycle in 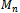 contains an equal number of edges of each colour.ProofThe middle level graph contains two sets of verities; one containing
contains an equal number of edges of each colour.ProofThe middle level graph contains two sets of verities; one containing 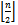 ones and
ones and 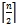 zeros and the other containing
zeros and the other containing 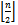 zeros and
zeros and 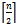 ones. Suppose we fix the
ones. Suppose we fix the 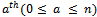 bit of a vertex in the first set to one and the
bit of a vertex in the first set to one and the 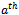 bit of a vertex in the second set to a zero. It follows then
bit of a vertex in the second set to a zero. It follows then 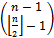 strings from the first set will contain a one in the
strings from the first set will contain a one in the 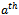 bit position and
bit position and 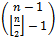 strings from the second set will contain a zero in the
strings from the second set will contain a zero in the 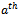 bit position. Similarly, the number of strings from the first set containing a zero in
bit position. Similarly, the number of strings from the first set containing a zero in 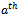 bit position is equal to the number of strings from the second set containing a one in the
bit position is equal to the number of strings from the second set containing a one in the 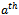 position:
position: 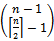 . Thus, the total number of strings in the middle level containing a one in the
. Thus, the total number of strings in the middle level containing a one in the 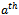 bit position equals the total number of strings containing a zero in that position, and there are an equal number of zeros and ones in each position. Since the Hamiltonian cycles of the graph contain each of the vertices of the graph, the number of bit changes for each position must be the same. This implies the number of edges of each colour is the same.
bit position equals the total number of strings containing a zero in that position, and there are an equal number of zeros and ones in each position. Since the Hamiltonian cycles of the graph contain each of the vertices of the graph, the number of bit changes for each position must be the same. This implies the number of edges of each colour is the same.
6. Computational Pattern Search
With code provided by Dr. Markov of Sofia University[5], Hamiltonian cycles were generated for 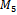 and
and 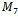 . The growth of the number of Hamiltonian cycles as the dimensions of the graphs increases is rather fantastic. It is clear that
. The growth of the number of Hamiltonian cycles as the dimensions of the graphs increases is rather fantastic. It is clear that 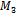 contains only one Hamiltonian Path, and for
contains only one Hamiltonian Path, and for 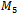 there are 24 Hamiltonian Cycles. For
there are 24 Hamiltonian Cycles. For 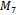 however, there are millions. All 24 paths for
however, there are millions. All 24 paths for 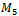 were generated with the provided code within a matter of seconds. After running the program for just shy of three straight days,
were generated with the provided code within a matter of seconds. After running the program for just shy of three straight days, 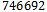 Hamiltonian cycles were found for
Hamiltonian cycles were found for 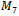 before the program was stopped.Using the collected data, subsequent programs were developed to search the cycles for particular properties within. Various queue Gray code properties were searched as well as the antipodal property.
before the program was stopped.Using the collected data, subsequent programs were developed to search the cycles for particular properties within. Various queue Gray code properties were searched as well as the antipodal property.
6.1. -shift Queue Gray Code
As earlier stated, a queue Gray code sequence is a sequence of binary strings in which consecutive words differ by a single bit and are constructed by removing the most significant bit, shifting the remaining bits one digit left and, appending a new least significant bit. Since ‘101’ is an illegal substring, and 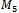 will contain the string ‘10101’
will contain the string ‘10101’ 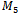 cannot contain a Hamiltonian path which is a queue Gray code sequence. Similarly,
cannot contain a Hamiltonian path which is a queue Gray code sequence. Similarly, 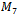 contains the string ‘1010101’ and any larger middle layer graph will contain a similar illegal string.
contains the string ‘1010101’ and any larger middle layer graph will contain a similar illegal string.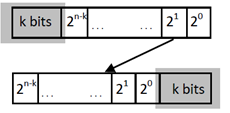 | Figure 10. Generalized k-shift Queue Gray code |
Consider, alternatively, what would occur if the shift was generalized. Suppose that rather than considering a bit shift of one, a shift of two or three was considered. Let 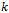 be the number of bits to be shifted, and a
be the number of bits to be shifted, and a 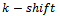 refer to a queue Gray code shift of
refer to a queue Gray code shift of 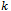 bits (Fig. 10). As earlier stated, no cycles will exist when
bits (Fig. 10). As earlier stated, no cycles will exist when 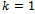 . In the case where a
. In the case where a 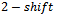 was considered, the program found no cycles in
was considered, the program found no cycles in 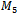 or
or 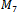 containing the queue Gray code shift. This too makes sense considering a substring a of ‘0011’ will exist in at least one of the vertices’ strings and this substring, if a
containing the queue Gray code shift. This too makes sense considering a substring a of ‘0011’ will exist in at least one of the vertices’ strings and this substring, if a 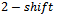 is applied, will fail to be a Gray code transition. Moving to a
is applied, will fail to be a Gray code transition. Moving to a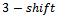 , again no cycles were found. This is reasonable given that some vertex will contain the substring ‘00011’. If a
, again no cycles were found. This is reasonable given that some vertex will contain the substring ‘00011’. If a 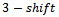 is applied to the word containing this substring then the two words will fail to be a Gray code sequence.Given the failure on all accounts where the shift is less than or equal to
is applied to the word containing this substring then the two words will fail to be a Gray code sequence.Given the failure on all accounts where the shift is less than or equal to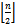 , we consider the case where any of the three shifts is acceptable. That is, between any consecutive vertex strings, a
, we consider the case where any of the three shifts is acceptable. That is, between any consecutive vertex strings, a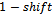 ,
, 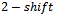 , or a
, or a 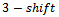 is permitted. This too failed to produce any results. There was no cycle in
is permitted. This too failed to produce any results. There was no cycle in 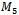 found to contain the property and none of the produced cycles for
found to contain the property and none of the produced cycles for 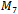 did either. Looking closer into the case of
did either. Looking closer into the case of 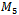 the reason for this is evident. All of the Hamiltonian cycles in
the reason for this is evident. All of the Hamiltonian cycles in 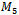 contain at least one of the following pairs of consecutive vertices (decimal):,
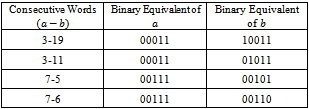
contain at least one of the following pairs of consecutive vertices (decimal):, 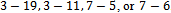 . Looking at their binary equivalents (Table 2) it is clear that all these consecutive words do not contain any
. Looking at their binary equivalents (Table 2) it is clear that all these consecutive words do not contain any 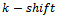 for
for 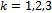 .
.Table 2. Consecutive Vertices of M5
 |
| |
|
6.2. Antipodal Paths/Cycles
A cycle in known as antipodal if opposite nodes of the cycle are complementary bit strings. When the nodes are binary strings this simply means that opposite strings hold zeros and ones in opposite positions and the sum of the two strings will be a string of all ones (the largest binary number possible for strings of that length). For example, consider the middle level graph in the third dimension. When each of the six binary strings are arranged evenly in a circular pattern the opposite vertices have a sum of ‘111’. In the positions where one of the strings has zeros, its opposite string holds ones and where this string holds zeros the other has ones (Fig. 11). This idea can easily be extended to paths by considering opposite vertices to be those separated by 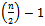 strings, where n is the even number of strings in the sequence and each vertex is represented by string.
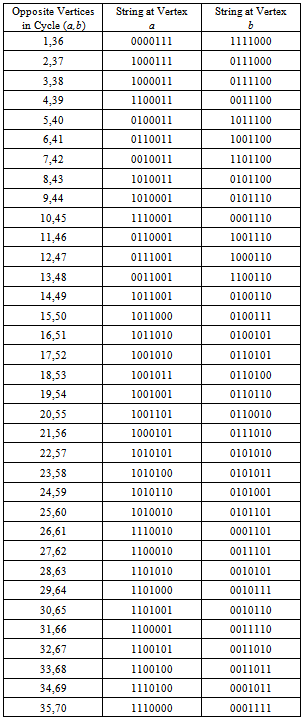
strings, where n is the even number of strings in the sequence and each vertex is represented by string.Table 3. Antipodal Hamiltonian Cycle in M7
 |
| |
|
As it is clear from Fig. 11, the antipodal property holds for the Hamiltonian cycle in the middle level of a 3-dimmensional cube. For the middle level graphs of higher dimension where there are more Hamiltonian cycles, whether an antipodal one exists or not, is not so apparent.We developed a program to search for this property in 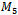 and
and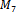 . Results reveal that no Hamiltonian cycle in
. Results reveal that no Hamiltonian cycle in 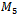 is antipodal. However, there were numerous, at least thousands, of cycles in
is antipodal. However, there were numerous, at least thousands, of cycles in 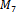 which were. One such cycle is given in Table 3 below.
which were. One such cycle is given in Table 3 below.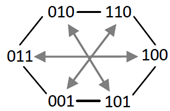 | Figure 11. Antipodal Property of M3 |
7. Conclusions
The difficulty in solving the middle level conjecture lies in part in the fact that patterns are difficult to find. There doesn’t appear to be any clear consistent pattern among the Hamiltonian cycles of the middle level graphs. Though all such cycles will inevitably be cyclic Gray code sequences, every path within any binary hypercube will also be a Gray code sequence. However, it can be said that like the hybercube, and the middle level graph, every Hamiltonian cycle in a middle level graph will contain an equal number of edges of each colour when colouring is based on the weight of the bit being changed between the adjacent vertices. As far as queue Gray code is concerned, no patterns can be found (within the first three middle level graphs at least) as no queue Gray code cycles could be found even with a flexible bit shift. Antipodal cycles however, do exist but not consistently throughout all dimensional graphs. The elusive nature of the Hamiltonian cycle in middle level graphs makes it difficult to derive any feasible algorithmic method for their discovery.To put this in a larger context, the study of the Middle Level Conjecture has contributed new ideas and methods to combinatorics[8]. As we already mentioned, the computational results strengthen the belief that the conjecture is true. If and when it is finally settled this will not be a breakthrough. However, the work on it during the last three decades has illuminated other areas and influenced them. One of the primary beneficiaries is the study of Gray codes. The general question here, given the hamiltonicity of the binary hypercube is to find smaller/restricted structures [12] that admit Gray codes (the middle level is one of them), and conversely find a structure in Gray codes that have certain restrictions imposed on them: the queue property, the generalized queue property or similar. To this end, we would like to mention that it is conjectured that a Hamiltonian cycle exists not only in the k-th and 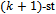 level of the (2k+1)- dimensional hypercube, but between the k-th and (n-k)-th level of the n-dimensional hypercube under the generalized notion of adjacency through
level of the (2k+1)- dimensional hypercube, but between the k-th and (n-k)-th level of the n-dimensional hypercube under the generalized notion of adjacency through 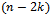 bit flips instead of a single bit flip. Many research articles in recent years [7, 9, 10, 11, 13, 14] offer methods for finding large cycles in the middle layer and hope that these techniques can be extended towards general proof of hamiltonicity.
bit flips instead of a single bit flip. Many research articles in recent years [7, 9, 10, 11, 13, 14] offer methods for finding large cycles in the middle layer and hope that these techniques can be extended towards general proof of hamiltonicity.
ACKNOWLEDGEMENTS
Dr. Tzvetalin Vassilev’s research is supported by NSERC Discovery Grant. Joanna Ammerlaan wishes to acknowledge the help and support of Dr. Tzvetalin Vassilev during the work on this paper. Both authors acknowledge the discussions with, and the helpful suggestions of Dr. Minko Markov and Dr. Darko Dimitrov throughout the work on this topic. We are particularly thankful to Dr. Markov for sharing his computational results and code with us. Finally, we want to acknowledge the participants of the Annual Workshop on Algorithmic Graph Theory held at Nipissing University since 2010 for their inspirational talks.
References
| [1] | B. West, Revolving Door (Middle Levels) Conjecture: Open Problems – Graph Theory and Combinatorics, homepage on Mathematics, University of Illinois[Online]. Available at: http://www.math.uiuc.edu/~west/openp/revolving.html |
| [2] | D. Marcus, Graph Theory: A Problem Oriented Approach, MAA, Washington, USA, 2008. |
| [3] | G. Moss, R. Tocci, N. Widmer, Digital Systems Principles and Applications, 10th Edition. Victoria, Canada. Pearson Education, 2006. |
| [4] | D. Dimitrov, Gray Codes Avoiding or Containing Given Matchings. Workshop on Algorithmic Graph Theory, Nipissing University, North Bay, Canada, May 17 – 22, 2010. |
| [5] | M. Markov, On the Middle Level Conjecture in the Hypercube. 3rd Annual Workshop on Algorithmic Graph Theory, Nipissing University, North Bay, Canada, June 4 – 8, 2012. |
| [6] | P. P. Parkhomenko, Classification of the Hamiltonian Cycles in Binary Hypercubes. Russian Academy of Sciences, Moscow, Russia, January, 2001. |
| [7] | T. Mutze and F. Weber, Construction of 2-Factors in the Middle Layer of the Discrete Cube. Technical Report, ETH Zurich, 2011. |
| [8] | I. Shields, B. Shields, and C. Savage. An update on the middle levels problem. Discrete Mathematics, 309(17): 5271–5277, 2009. |
| [9] | M. Shimada and K. Amano. A Note on the Middle Levels Conjecture. arXiv:0912.4564, September 2011. |
| [10] | H. Kierstead and W. Trotter. Explicit Matchings in the Middle Levels of the Boolean Lattice. Order, 5(2): 163–171, 1988. |
| [11] | J. Johnson. Long Cycles in the Middle Two Layers of the Discrete Cube. J. Combin. Theory Ser. A, 105(2): 255–271, 2004. |
| [12] | M. Buck and D. Wiedemann. Gray Codes with Restricted Density. Discrete Mathematics, 48(2-3) :163–171, 1984. |
| [13] | D. Duffus, H. Kierstead, and H. Snevily. An Explicit 1-Factorization in the Middle of the Boolean Lattice. J. Combin. Theory Ser. A, 65(2): 334–342, 1994. |
| [14] | I. Shields and C. Savage, A Hamilton Path Heuristic with Applications to the Middle Two Levels Problem, Congressus Numerantium, 140: 161-178, 1999. |

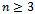 , there exists a Hamiltonian cycle in the graph of the middle layers of the hypercube. The difficulty in solving the problem is undoubtedly due in part to the unclear nature of Hamiltonian cycles in general, for there is no known method to prove the existence of a Hamiltonian cycle in a graph. There are a few strategies which can be used to disprove the existence of such cycles [2], but the middle level graph, as little effort will show, fails on these accounts. As of 2006, with the aid of technology,
, there exists a Hamiltonian cycle in the graph of the middle layers of the hypercube. The difficulty in solving the problem is undoubtedly due in part to the unclear nature of Hamiltonian cycles in general, for there is no known method to prove the existence of a Hamiltonian cycle in a graph. There are a few strategies which can be used to disprove the existence of such cycles [2], but the middle level graph, as little effort will show, fails on these accounts. As of 2006, with the aid of technology, 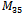 and
and 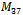 were the largest graphs of this nature to be proved to contain Hamiltonian cycles [5, 9]. This paper takes a look at various properties of the hypercube and the middle level graph as well as the use of Gray codes to develop some of these properties. Finally, this paper will look into how queue Gray codes can be used to search for paths and cycles within middle level graphs and the results of queue Gray code and antipodal tests on known Hamiltonian paths within various middle level graphs.
were the largest graphs of this nature to be proved to contain Hamiltonian cycles [5, 9]. This paper takes a look at various properties of the hypercube and the middle level graph as well as the use of Gray codes to develop some of these properties. Finally, this paper will look into how queue Gray codes can be used to search for paths and cycles within middle level graphs and the results of queue Gray code and antipodal tests on known Hamiltonian paths within various middle level graphs.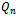 , where n is the dimension (Fig. 1).
, where n is the dimension (Fig. 1).
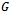 a path that contains every vertex of
a path that contains every vertex of 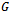 once is referred to as a Hamiltonian Path [2].Definition 3 (Hamiltonian Cycle)In a graph
once is referred to as a Hamiltonian Path [2].Definition 3 (Hamiltonian Cycle)In a graph 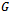 , a cycle c of
, a cycle c of 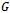 , which contains every vertex of
, which contains every vertex of 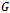 once, is said to be a Hamiltonian cycle, and for this reason,
once, is said to be a Hamiltonian cycle, and for this reason, 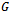 is called a Hamiltonian graph[2].Definition 4 (Vertex Levels of a Hypercube)When mapped to a coordinate axis, each vertex of a hypercube,
is called a Hamiltonian graph[2].Definition 4 (Vertex Levels of a Hypercube)When mapped to a coordinate axis, each vertex of a hypercube, 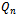 , can be assigned a binary string of length n. The
, can be assigned a binary string of length n. The 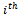 level of the hypercube refers to the set of vertices of
level of the hypercube refers to the set of vertices of 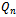 which contain I ones in their vertex string (Fig. 2).Definition 5 (Middle Level Graph)The middle layer graph, denoted
which contain I ones in their vertex string (Fig. 2).Definition 5 (Middle Level Graph)The middle layer graph, denoted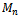 , is a subgraph of
, is a subgraph of 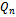 containing the vertices in levels
containing the vertices in levels 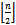 and
and 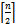 (Fig. 2).Definition 6 (Word or String)The terms word and string are used interchangeably to refer to a binary number consisting of a sequence of zeros and ones.
(Fig. 2).Definition 6 (Word or String)The terms word and string are used interchangeably to refer to a binary number consisting of a sequence of zeros and ones.
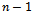 , and its reflection and appending a zero bit to the left side of the unreflected words and a one bit to the left of the reflected words (Fig. 3). The result is a sequence of 2n words of length n where the first and the last differ by a single bit. Continuing, in this manner inductively, a cyclic Gray code sequence can be produced for all words of length n.
, and its reflection and appending a zero bit to the left side of the unreflected words and a one bit to the left of the reflected words (Fig. 3). The result is a sequence of 2n words of length n where the first and the last differ by a single bit. Continuing, in this manner inductively, a cyclic Gray code sequence can be produced for all words of length n.
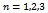

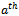 bit in the string. The first ones bit immediately to left of
bit in the string. The first ones bit immediately to left of 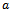 in the
in the 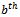 bit of the substring, and the first ones bit immediately to the right of
bit of the substring, and the first ones bit immediately to the right of 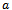 be in the
be in the 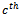 bit of the substring.In the next consecutive word, all the bits of the substring will be shifted one bit to the left. Consider this new word. In the
bit of the substring.In the next consecutive word, all the bits of the substring will be shifted one bit to the left. Consider this new word. In the 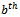 position there will be a zero and in the
position there will be a zero and in the 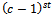 position there will be a one. Since the previous consecutive word contained a one and a zero respectively in these positions, two bits have changed between words (Fig. 5). Thus, the shift is not a Gray code shift: a contradiction.
position there will be a one. Since the previous consecutive word contained a one and a zero respectively in these positions, two bits have changed between words (Fig. 5). Thus, the shift is not a Gray code shift: a contradiction.
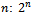 . The degree of each vertex is the dimension n and adjacent vertices differ by a single bit.
. The degree of each vertex is the dimension n and adjacent vertices differ by a single bit. 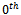 layer containing no ones and the
layer containing no ones and the 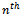 layer containing only ones (Fig. 7).It is apparent that edges only exist between consecutive vertex layers of the graph and not between edges of the same layer. This follows from the fact that edges only exist between vertices which differ by one bit; that is, one endpoint of an edge will contain one more one than the other. Thus, the layered graph will only contain edges between consecutive layers. It is readily apparent then that the graph of a hypercube is also bipartite.
layer containing only ones (Fig. 7).It is apparent that edges only exist between consecutive vertex layers of the graph and not between edges of the same layer. This follows from the fact that edges only exist between vertices which differ by one bit; that is, one endpoint of an edge will contain one more one than the other. Thus, the layered graph will only contain edges between consecutive layers. It is readily apparent then that the graph of a hypercube is also bipartite. 
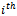 vertex layer of a hypercube contains
vertex layer of a hypercube contains 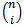 vertices and between vertex layers
vertices and between vertex layers 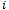 and
and 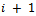 there exists an edge layer containing
there exists an edge layer containing 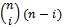 or equivalently
or equivalently 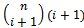 edges.
edges.
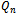 by considering the Gray code sequence of length n. Beginning at the origin, the vertex whose word is a string of n zeros, each consecutive vertex in the path is simply the consecutive Gray code word. These vertices will be adjacent because their binary strings differ by a single bit (as per the definition of Gray code). Since a Gray code sequence will exist through all
by considering the Gray code sequence of length n. Beginning at the origin, the vertex whose word is a string of n zeros, each consecutive vertex in the path is simply the consecutive Gray code word. These vertices will be adjacent because their binary strings differ by a single bit (as per the definition of Gray code). Since a Gray code sequence will exist through all 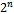 possible strings, it follows that a Hamiltonian path will exists.It can similarly be shown that the hypercube is Hamiltonian. In this case we simply consider the reflected Gray code sequences. Again, because this cyclic sequence exists and is of length
possible strings, it follows that a Hamiltonian path will exists.It can similarly be shown that the hypercube is Hamiltonian. In this case we simply consider the reflected Gray code sequences. Again, because this cyclic sequence exists and is of length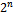 , a Hamiltonian cycle will exist in
, a Hamiltonian cycle will exist in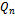 .
.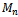 is a subgraph of
is a subgraph of 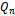 containing those vertices in levels
containing those vertices in levels 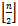 and
and 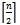 and the edges between them. When n is even however,
and the edges between them. When n is even however, 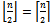 and the subgraph contains only vertices on a single middle layer. Since no edges exist between vertices in the same vertex layer, each vertex will have a degree of zero and the graph will be completely disconnected. No Hamiltonian path or cycle could possibly exist. When n is odd, Hamiltonicity is less clear.
and the subgraph contains only vertices on a single middle layer. Since no edges exist between vertices in the same vertex layer, each vertex will have a degree of zero and the graph will be completely disconnected. No Hamiltonian path or cycle could possibly exist. When n is odd, Hamiltonicity is less clear.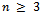 ,
, 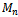 is Hamiltonian.When
is Hamiltonian.When 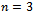 , the only Hamiltonian cycle in
, the only Hamiltonian cycle in 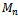 is rather trivial as it is also an Euler path and the total number of edges is only 6 (middle level of Fig. 2). It is considerably more difficult to locate a Hamiltonian cycle in
is rather trivial as it is also an Euler path and the total number of edges is only 6 (middle level of Fig. 2). It is considerably more difficult to locate a Hamiltonian cycle in 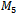 , despite the fact that the graph contains several such cycles (Fig. 9).
, despite the fact that the graph contains several such cycles (Fig. 9).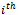 bit, is equivalent to the weight of the
bit, is equivalent to the weight of the 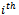 position in the string.
position in the string. 
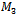 the Hamiltonian path is a sequence of alternating colours
the Hamiltonian path is a sequence of alternating colours 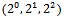 and the graph contains the same number of edges of each colour. This is also the case with
and the graph contains the same number of edges of each colour. This is also the case with 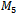 . Though there does not appear to be a clear pattern between the edge colours in the Hamiltonian cycles, there remains four edges of each colour in the cycles.
. Though there does not appear to be a clear pattern between the edge colours in the Hamiltonian cycles, there remains four edges of each colour in the cycles.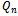 contains an equal number of edges of each colour.Proof (Please refer to Fig. 7)Let
contains an equal number of edges of each colour.Proof (Please refer to Fig. 7)Let 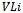 refer to vertex level i and
refer to vertex level i and 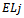 refer to edge level j which resides between
refer to edge level j which resides between 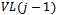 and
and 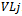 . Each of the j ones in
. Each of the j ones in 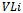 will refer to an edge in
will refer to an edge in 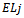 and following the edge to
and following the edge to 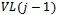 will result in a string missing one of the ones. Recall the position of the missing one determines the colour of the edge. We also know that each vertex will contain an edge of every colour, each corresponding to the axis represented by the changing bit.Beginning with
will result in a string missing one of the ones. Recall the position of the missing one determines the colour of the edge. We also know that each vertex will contain an edge of every colour, each corresponding to the axis represented by the changing bit.Beginning with 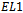 ,
, 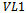 contains exactly
contains exactly 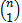 vertices representing each of the n possible positions of the ones bit in the word. It follows then that
vertices representing each of the n possible positions of the ones bit in the word. It follows then that 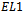 contains a single edge of each colour.
contains a single edge of each colour.
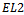 ,
, 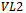 contains exactly
contains exactly  combinations of positions for the two ones in the words. Each of the
combinations of positions for the two ones in the words. Each of the 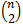 vertices will be adjacent to a pair of uniquely coloured edges in
vertices will be adjacent to a pair of uniquely coloured edges in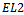 . By fixing one colour and choosing another from the remaining
. By fixing one colour and choosing another from the remaining 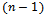 we get that there are
we get that there are 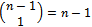 edges of each colour. Looking up to
edges of each colour. Looking up to 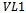 it can be seen that an edge of each colour extends down from each of the vertices to a vertex in
it can be seen that an edge of each colour extends down from each of the vertices to a vertex in 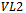 except for the vertex in
except for the vertex in 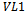 which is adjacent to
which is adjacent to 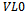 by an edge of that colour. The total number of edges in
by an edge of that colour. The total number of edges in 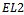 is confirmed by multiplying the number of vertices in
is confirmed by multiplying the number of vertices in 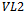 by their degree in
by their degree in 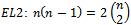 .Similarly,
.Similarly, 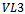 contains
contains 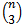 different vertices each containing a unique set of three coloured edges in
different vertices each containing a unique set of three coloured edges in 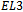 ,
, 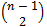 edges of each colour exist in
edges of each colour exist in 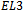 , and the total number of edges in
, and the total number of edges in 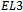 is equal to the product of number of edges of each colour and the number of colours:
is equal to the product of number of edges of each colour and the number of colours: 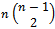 . The number of edges of each colour in
. The number of edges of each colour in 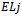 is
is 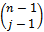 . Therefore, there are an equal number of edges of each colour in each of the edge layers.
. Therefore, there are an equal number of edges of each colour in each of the edge layers.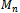 contains an equal number of edges of each colour.ProofThe middle level graph contains two sets of verities; one containing
contains an equal number of edges of each colour.ProofThe middle level graph contains two sets of verities; one containing 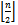 ones and
ones and 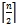 zeros and the other containing
zeros and the other containing 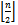 zeros and
zeros and 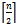 ones. Suppose we fix the
ones. Suppose we fix the 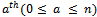 bit of a vertex in the first set to one and the
bit of a vertex in the first set to one and the 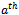 bit of a vertex in the second set to a zero. It follows then
bit of a vertex in the second set to a zero. It follows then 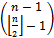 strings from the first set will contain a one in the
strings from the first set will contain a one in the 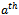 bit position and
bit position and 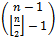 strings from the second set will contain a zero in the
strings from the second set will contain a zero in the 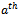 bit position. Similarly, the number of strings from the first set containing a zero in
bit position. Similarly, the number of strings from the first set containing a zero in 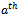 bit position is equal to the number of strings from the second set containing a one in the
bit position is equal to the number of strings from the second set containing a one in the 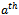 position:
position: 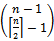 . Thus, the total number of strings in the middle level containing a one in the
. Thus, the total number of strings in the middle level containing a one in the 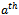 bit position equals the total number of strings containing a zero in that position, and there are an equal number of zeros and ones in each position. Since the Hamiltonian cycles of the graph contain each of the vertices of the graph, the number of bit changes for each position must be the same. This implies the number of edges of each colour is the same.
bit position equals the total number of strings containing a zero in that position, and there are an equal number of zeros and ones in each position. Since the Hamiltonian cycles of the graph contain each of the vertices of the graph, the number of bit changes for each position must be the same. This implies the number of edges of each colour is the same.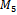 and
and 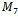 . The growth of the number of Hamiltonian cycles as the dimensions of the graphs increases is rather fantastic. It is clear that
. The growth of the number of Hamiltonian cycles as the dimensions of the graphs increases is rather fantastic. It is clear that 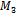 contains only one Hamiltonian Path, and for
contains only one Hamiltonian Path, and for 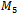 there are 24 Hamiltonian Cycles. For
there are 24 Hamiltonian Cycles. For 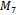 however, there are millions. All 24 paths for
however, there are millions. All 24 paths for 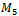 were generated with the provided code within a matter of seconds. After running the program for just shy of three straight days,
were generated with the provided code within a matter of seconds. After running the program for just shy of three straight days, 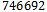 Hamiltonian cycles were found for
Hamiltonian cycles were found for 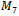 before the program was stopped.Using the collected data, subsequent programs were developed to search the cycles for particular properties within. Various queue Gray code properties were searched as well as the antipodal property.
before the program was stopped.Using the collected data, subsequent programs were developed to search the cycles for particular properties within. Various queue Gray code properties were searched as well as the antipodal property. 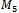 will contain the string ‘10101’
will contain the string ‘10101’ 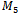 cannot contain a Hamiltonian path which is a queue Gray code sequence. Similarly,
cannot contain a Hamiltonian path which is a queue Gray code sequence. Similarly, 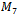 contains the string ‘1010101’ and any larger middle layer graph will contain a similar illegal string.
contains the string ‘1010101’ and any larger middle layer graph will contain a similar illegal string.
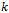 be the number of bits to be shifted, and a
be the number of bits to be shifted, and a 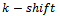 refer to a queue Gray code shift of
refer to a queue Gray code shift of 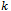 bits (Fig. 10). As earlier stated, no cycles will exist when
bits (Fig. 10). As earlier stated, no cycles will exist when 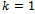 . In the case where a
. In the case where a 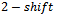 was considered, the program found no cycles in
was considered, the program found no cycles in 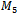 or
or 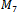 containing the queue Gray code shift. This too makes sense considering a substring a of ‘0011’ will exist in at least one of the vertices’ strings and this substring, if a
containing the queue Gray code shift. This too makes sense considering a substring a of ‘0011’ will exist in at least one of the vertices’ strings and this substring, if a 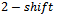 is applied, will fail to be a Gray code transition. Moving to a
is applied, will fail to be a Gray code transition. Moving to a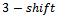 , again no cycles were found. This is reasonable given that some vertex will contain the substring ‘00011’. If a
, again no cycles were found. This is reasonable given that some vertex will contain the substring ‘00011’. If a 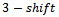 is applied to the word containing this substring then the two words will fail to be a Gray code sequence.Given the failure on all accounts where the shift is less than or equal to
is applied to the word containing this substring then the two words will fail to be a Gray code sequence.Given the failure on all accounts where the shift is less than or equal to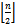 , we consider the case where any of the three shifts is acceptable. That is, between any consecutive vertex strings, a
, we consider the case where any of the three shifts is acceptable. That is, between any consecutive vertex strings, a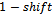 ,
, 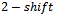 , or a
, or a 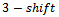 is permitted. This too failed to produce any results. There was no cycle in
is permitted. This too failed to produce any results. There was no cycle in 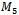 found to contain the property and none of the produced cycles for
found to contain the property and none of the produced cycles for 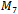 did either. Looking closer into the case of
did either. Looking closer into the case of 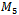 the reason for this is evident. All of the Hamiltonian cycles in
the reason for this is evident. All of the Hamiltonian cycles in 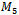 contain at least one of the following pairs of consecutive vertices (decimal):,
contain at least one of the following pairs of consecutive vertices (decimal):, 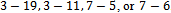 . Looking at their binary equivalents (Table 2) it is clear that all these consecutive words do not contain any
. Looking at their binary equivalents (Table 2) it is clear that all these consecutive words do not contain any 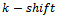 for
for 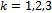 .
.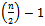 strings, where n is the even number of strings in the sequence and each vertex is represented by string.
strings, where n is the even number of strings in the sequence and each vertex is represented by string.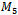 and
and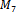 . Results reveal that no Hamiltonian cycle in
. Results reveal that no Hamiltonian cycle in 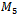 is antipodal. However, there were numerous, at least thousands, of cycles in
is antipodal. However, there were numerous, at least thousands, of cycles in 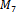 which were. One such cycle is given in Table 3 below.
which were. One such cycle is given in Table 3 below.
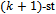 level of the (2k+1)- dimensional hypercube, but between the k-th and (n-k)-th level of the n-dimensional hypercube under the generalized notion of adjacency through
level of the (2k+1)- dimensional hypercube, but between the k-th and (n-k)-th level of the n-dimensional hypercube under the generalized notion of adjacency through 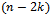 bit flips instead of a single bit flip. Many research articles in recent years [7, 9, 10, 11, 13, 14] offer methods for finding large cycles in the middle layer and hope that these techniques can be extended towards general proof of hamiltonicity.
bit flips instead of a single bit flip. Many research articles in recent years [7, 9, 10, 11, 13, 14] offer methods for finding large cycles in the middle layer and hope that these techniques can be extended towards general proof of hamiltonicity. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

