-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(6): 184-186
doi: 10.5923/j.am.20120206.01
The Limiting Probabilities in the Process of Servicing
Roza Shakenova
Kazach national technical university named after K. I. Satpaev, Almaty, Kazakhstan
Correspondence to: Roza Shakenova, Kazach national technical university named after K. I. Satpaev, Almaty, Kazakhstan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Using 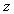 - transformation in Markov processes connected with the fact that the probabilities of transition for the
- transformation in Markov processes connected with the fact that the probabilities of transition for the 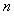 steps in them are geometric progressions, so that with the help of
steps in them are geometric progressions, so that with the help of 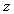 -transformation expression for these probabilities can be obtained in analytical form.
-transformation expression for these probabilities can be obtained in analytical form.
Keywords: limiting probability, Probability of state, Markov Processes, Z-transform
Cite this paper: Roza Shakenova, "The Limiting Probabilities in the Process of Servicing", Applied Mathematics, Vol. 2 No. 6, 2012, pp. 184-186. doi: 10.5923/j.am.20120206.01.
Article Outline
1. Introduction
- Markov chain with a countable state space is an interesting part of Markov processes. Markov processes have found wide application in the application of probability theory and statistics. Some of these applications require more specific information. Other applications require great community. The first type consists of finite chains. The second type includes various models of queuing. Markov process in the study of complex systems is the most convenient. The concepts of the system and the transitions from one state to another are attractive. Since AA Markov introduced the concepts of this theory; many of the leading mathematicians of the world as Richard A. Howard, John Kemeny and others continued to develop the theory of Markov chains. Application of z-transformation for determining the limit probability of markovian processes is shown in the article. In the problem of maintenance of machines can also use the z-transformation. Using z-transformation the expression for the probability can be obtained in an analytical form. And also with z-transformation can find exact analytical expressions of probability states.
2. The Use of 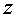 - transforms the Problem of Maintenance of Machines
- transforms the Problem of Maintenance of Machines
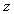 - Transformation can be defined as follows:
- Transformation can be defined as follows: 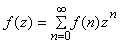 | (1) |
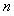 as time, then the function
as time, then the function 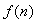 takes arbitrary values of
takes arbitrary values of 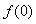 ,
, 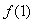 ,
, 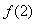 , ... for positive time
, ... for positive time 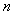 , equal to zero for negative. Function
, equal to zero for negative. Function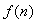 and its transformation
and its transformation 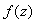 are related to-one correspondence, for example, the unit step function
are related to-one correspondence, for example, the unit step function 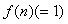 corresponds to its
corresponds to its 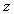 - transformation
- transformation 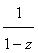 , and
, and 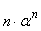 matches
matches 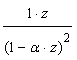 . Consider the problem of maintenance of machines [2]. The machine can be serviced periodically, e.g once per hour. At every moment, there are two states. One working, and another - failing (state 2). If a machine fails, it can be restored to full working condition. The probability to remain in state 1 is equal to 0.7, while the probability to move to state 2 is equal to 0.3. And if the machine is in failing state, then the probability of transition to state 1 is equal to 0.6, and stay in failing state is 0.4. The transition matrix in this case is represented as:
. Consider the problem of maintenance of machines [2]. The machine can be serviced periodically, e.g once per hour. At every moment, there are two states. One working, and another - failing (state 2). If a machine fails, it can be restored to full working condition. The probability to remain in state 1 is equal to 0.7, while the probability to move to state 2 is equal to 0.3. And if the machine is in failing state, then the probability of transition to state 1 is equal to 0.6, and stay in failing state is 0.4. The transition matrix in this case is represented as: We obtain:
We obtain: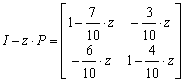 | (2) |
 So as
So as
 Then we obtain:
Then we obtain: The latter matrix can be represented as the sum of two terms, but until then we make the following:
The latter matrix can be represented as the sum of two terms, but until then we make the following: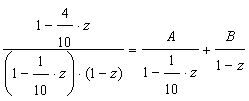 From this we obtain:
From this we obtain: 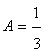 ,
, 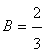 .Then:
.Then: 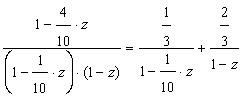 For the following element of matrix we obtain:
For the following element of matrix we obtain: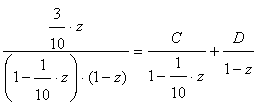 From this we find:
From this we find: 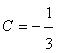 ,
,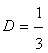 .Then:
.Then: 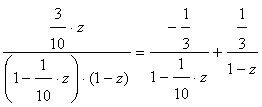 For the next element of transient matrix we obtain:
For the next element of transient matrix we obtain: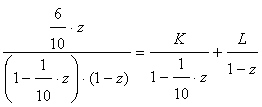 After defining
After defining 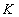 and
and 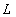
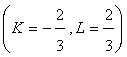 we obtain:
we obtain: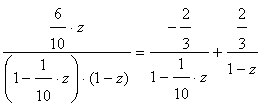 Now let’s calculate the last element:
Now let’s calculate the last element: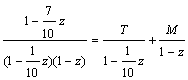 After finding
After finding 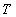 and
and 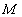 ,
, 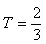 ,
, 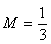 , we get the following expression:
, we get the following expression: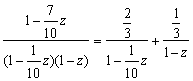 As a result transient matrix is expressed as the sum of two terms:
As a result transient matrix is expressed as the sum of two terms: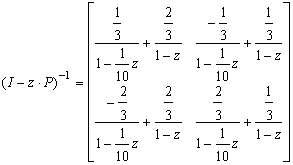 Or in the following way:
Or in the following way: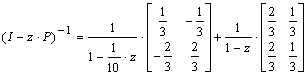 The inverse transform of this matrix, denoted in the form
The inverse transform of this matrix, denoted in the form 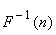 will be:
will be: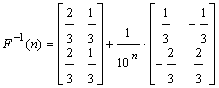 If the machine is in working condition (state 1), ie
If the machine is in working condition (state 1), ie 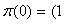
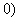 , then
, then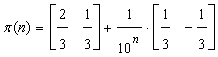 or
or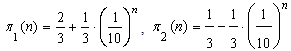 Moreover
Moreover 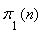 and
and 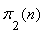 are the exact analytical expressions of the probabilities of states.If
are the exact analytical expressions of the probabilities of states.If 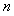 increases indefinitely, then
increases indefinitely, then 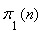 tends to
tends to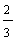 , and
, and 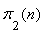 tends to
tends to 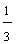 , that is, they are approaching to the limit state probabilities of the process. If the machine is in state 2, or
, that is, they are approaching to the limit state probabilities of the process. If the machine is in state 2, or 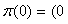
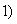 , then
, then 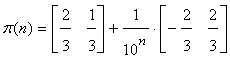 , or
, or 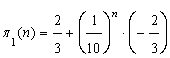
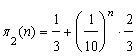 . You can see that with the growth of
. You can see that with the growth of 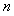 probabilities of the states are approaching to the limit probabilities of the process:
probabilities of the states are approaching to the limit probabilities of the process: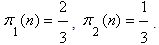 Thus we see that the marginal probabilities do not depend on the values of the probabilities of the initial state of the process. This is the ergodicity of these processes.
Thus we see that the marginal probabilities do not depend on the values of the probabilities of the initial state of the process. This is the ergodicity of these processes.3. Conclusions
- With the help of z-transformation we obtain exact analytical expressions of probability. Thus we see that the marginal probabilities in the problem of maintenance of machines do not depend on the values of the probabilities of the initial state of the process. This is the ergodicity of these processes. The following works on Markov processes [1], [6], [10] may be mentioned as good. The problem of maintenance of machinery has important meaning for the industry, as this problem leads to the problem of replacing the equipment. If there is a task of replacing equipments, you will see the following problem - which car to buy? Particularly the problem of maintenance of machinery concerned residents, owners of cars in countries, which do not specialize in the production of machines and equipment for cars. For ergodic chains sufficiently large period of operation comes stationary mode, in which the probabilities of the system states are independent of time and independent of the probability distribution at the initial time. Ergodic dynamical systems are convenient because they can be described by statistical methods with enough observation time. The system passes every state with definite probability. Therefore, this matrix can be constructed from statistics dates. Abstract matrix is not appropriate to be applied in such cases. If the matrix is stochastic, the sum of elements of any line is equal to 1. And any abstract matrix is not required to satisfy this condition.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML