-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(5): 166-170
doi: 10.5923/j.am.20120205.03
Performance Modeling and Study of blood Flow in Vessels with Porous Effects
Anil Kumar 1, C L Varshney 2, Veer Pal Singh 2
1Greater Noida Institute of technology ,Greater Noida , GB Nagar UP India
2Shri Varshney College Aligarh , UP India
Correspondence to: Anil Kumar , Greater Noida Institute of technology ,Greater Noida , GB Nagar UP India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we consider a mathematical model of blood flow in the blood vessels in presence of magnetic field with effects of porous is investigated. We have discussed the two phase model for the blood flow consisting of a central core of suspended erythrocytes and cell–free layer surrounding the core. The governing equations have been solved analytically. We have obtained the results for velocity, flow rate and effective viscosity in presence of peripheral layer and permeability parameter. All the result has been obtained and discussed through graphs. Physical interpretation of obtained expressions is shown here for better understanding of the problem.
Keywords: Hematocrit , Flow Rate, Viscosity, Permeability, Peripheral Layer, Magnetic Field, Hypertension.
Cite this paper: Anil Kumar , C L Varshney , Veer Pal Singh , "Performance Modeling and Study of blood Flow in Vessels with Porous Effects", Applied Mathematics, Vol. 2 No. 5, 2012, pp. 166-170. doi: 10.5923/j.am.20120205.03.
Article Outline
1. Introduction
- The control of the blood pressure has been possible by using porous effect in cases of cholesterol and related diseases. The plasma solution in the blood obeys the linear Newtonian model for viscosity[1]. The experimental observations and theoretical analysis of blood flow are very useful for the diagnosis of a number of cardiovascular diseases and development of pathological patterns in animal or human physiology[2].The flow of blood through small diameter tubes is of physiological and clinical importance. Due to its complexity and anomalous behaviour, it is very difficult to analyse it. The two types of anomaly are due to low shear and high shear effects[3].When blood flows through larger diameter arteries at high shear rates, it behaves like a Newtonian fluid. Singh and Gupta[4] investigated a computational study of porous medium on flow of non Newtonian liquid. Pries et al.[5] studied the effect of the tube diameter and the hematocrit ratio on the blood viscosity and found that for tube diameters greater than 1 mm, the blood viscosity is independent of the diameter while for tube diameter less than 1 mm, the blood viscosity is strongly dependent on the tube diameter. They also reported the viscosity increases non-linearly with the hematocrit. Bugliarello and Sevilla[6],Cokelet[7] and[8,9,10] have reported that for blood flowing through narrow blood vessels, there is a peripheral layer of plasma and a core region of suspension of all the erythrocytes.Also the red blood cell is major bio-magnetic substance and the blood flow may be influenced by the magnetic field[11]. The effect of magnetic field on blood flow has been analysed theoretically by treating blood as an electrically conductive fluid[12].Assuming blood as a magnetic fluid, it may be possible to control blood pressure and its flow behaviour by using an appropriate magnetic field. Most of the models[13]-[17] on blood flow deal with one phase model. However, in view of the fact that blood is a suspension, a two-phase model appears to be more appropriate. Wagh and Wagh[18] have used[19] a model of dusty gas to study the effect of the magnetic nature of red blood cells of the flow of blood. The reason is, blood is a liquid suspension having mass and volume concentrations roughly the same, however, for dusty gas the mass and bulk concentrations are quite different[20], Nayfeh’s[21] two phase model seems to be more suitable for blood flow. In the above mentioned studies, no attempt has been made to study the effect of magnetic field on stenosis under porous medium together[Gupta (23)]. Kumar et al.[24] investigated a computational technique for flow in blood vessels with porous effects. Gupta[25] investigated computational study of blood flow through stenosed artery with magnetic effects. In view of the above mentioned fact, we have considered the two phase model consisting of central core of suspended erythrocyte and cell free layer surrounding the core in the effect of porous. The study of flow under the influence of a porous effect is also important as far as flow and resistance are concerned. In the present investigation, we study the motion of the blood through a very narrow capillary under the action of the porous effects.
2. Mathematical Model
- We have considered a two layer model (Fig.1) for the blood flow within the cylindrical vessel of radius R consisting of central core radius R1, which contains an erythrocyte suspension of uniform hematocrit and a cell free layer outside the core containing plasma. We have taken some assumptions for formulating the mathematical model. Blood is considered as viscous, incompressible and electrically conducting fluid. Fluid flow is steady and laminar. Magnetic field is constant in transverse direction
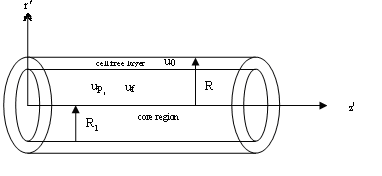 | Figure 1. Flow geometry of blood vessels |
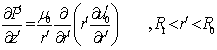 | (1) |
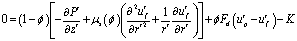 | (2) |
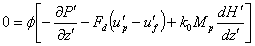 | (3) |
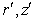 are radial and axial co-ordinates, K is the permeability parameter, uf and up are the velocities of the fluid (plasma) and particles (red cell),
are radial and axial co-ordinates, K is the permeability parameter, uf and up are the velocities of the fluid (plasma) and particles (red cell), 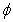 is the volume fraction of the red cells,
is the volume fraction of the red cells, 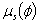 is the suspension viscosity, Fd is the drag coefficient of interaction for the force exerted by one phase on the other, k0 is the magnetic permeability, Mp is the magnetization of red cells and
is the suspension viscosity, Fd is the drag coefficient of interaction for the force exerted by one phase on the other, k0 is the magnetic permeability, Mp is the magnetization of red cells and 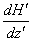 is the magnetic field gradient. The expression of the drag coefficient is given by:
is the magnetic field gradient. The expression of the drag coefficient is given by: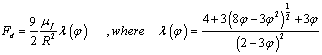 Where
Where 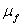 is the constant fluid viscosity.The viscosity of the suspension is given by an empirical relation.
is the constant fluid viscosity.The viscosity of the suspension is given by an empirical relation.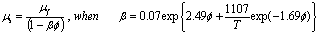 Boundary Conditions
Boundary Conditions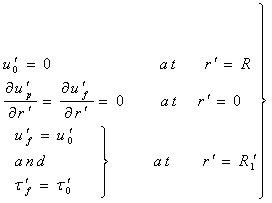 | (4) |
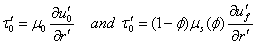
3. Solution of the Problem
- Introducing the following non-dimensional quantities are as given as:
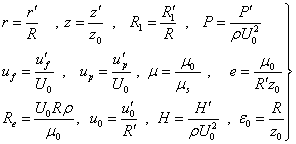 | (5) |
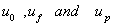 ,obtained as the solution of equations (1)-(3), subjected to the boundary conditions are given as:
,obtained as the solution of equations (1)-(3), subjected to the boundary conditions are given as: 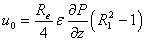 | (6) |
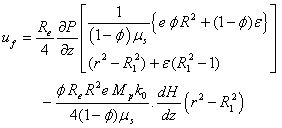 | (7) |
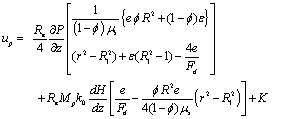 | (8) |
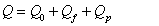 | (9) |
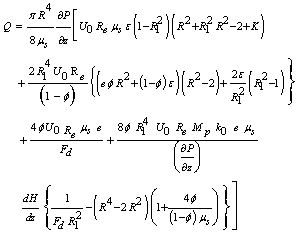 | (10) |
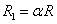 | (11) |
 | (12) |
4. Results and Discussions
- Results have been numerically worked out for various combinations of the parameters involved in the solution. To have a quantitave estimate of the various parameters involved, particularly the hematocrit (
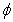 ) and magnetic field gradient
) and magnetic field gradient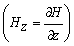 , some of the results is plotted graphically in fig. 2-8.The variation of effective viscosity (
, some of the results is plotted graphically in fig. 2-8.The variation of effective viscosity (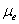 ) for different values of magnetic field gradient (
) for different values of magnetic field gradient (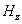 ) is shown in fig.2 and for different values of hematocrit (
) is shown in fig.2 and for different values of hematocrit (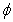 ) is shown in fig.3.The effective viscosity increases with increasing value of hematocrit. Also,the effective viscosity increases with the increase of the magnetic field gradient. This property in a static magnetic field increases the friction of the flowing blood,because the anisotropic orientation of the RBC in the static magnetic field distribes the rolling of the cell in flowing blood,and so the blood viscosity increases[22].
) is shown in fig.3.The effective viscosity increases with increasing value of hematocrit. Also,the effective viscosity increases with the increase of the magnetic field gradient. This property in a static magnetic field increases the friction of the flowing blood,because the anisotropic orientation of the RBC in the static magnetic field distribes the rolling of the cell in flowing blood,and so the blood viscosity increases[22].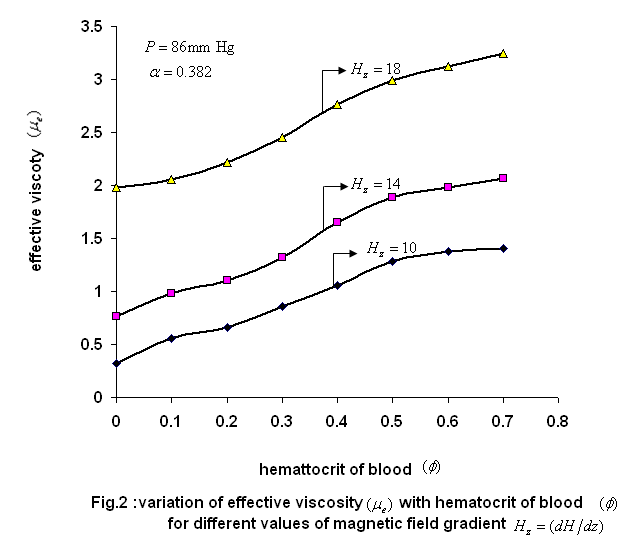 | Figure 2. variation of effective viscosity (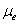 )with hematocrit of blood ( )with hematocrit of blood (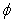 )for various values of magnetic field gradient )for various values of magnetic field gradient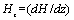 |
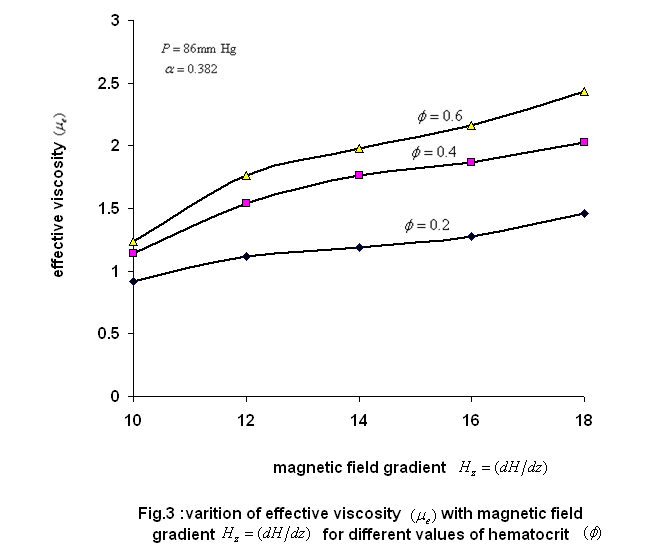 | Figure 3. variation of effective viscosity (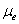 )with magnetic field gradient ( )with magnetic field gradient (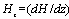 ) for different values of hematocrit field gradient ( ) for different values of hematocrit field gradient (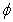 ), K=1.0 ), K=1.0 |
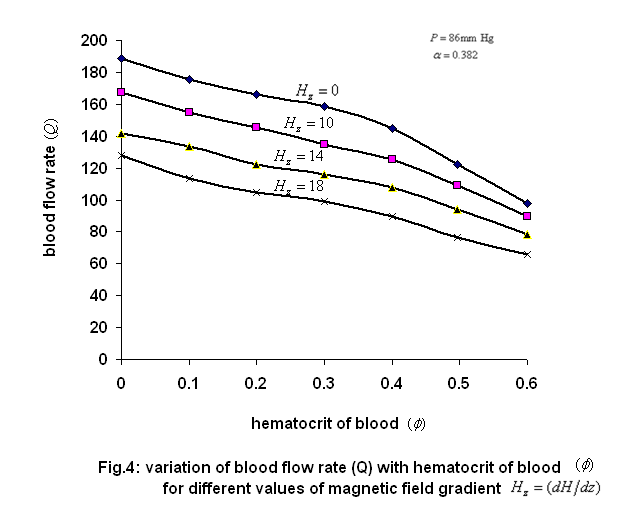 | Figure 4. variation of blood flow rate (Q)with hematocrit of blood (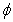 )for different values of magnetic field gradient )for different values of magnetic field gradient 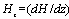 , K=2.0 , K=2.0 |
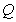 ) with hematocrit of blood (
) with hematocrit of blood (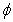 ) for different values of magnetic field gradient (
) for different values of magnetic field gradient (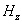 ). It is clear from the figure that the flow rate decreases slowly with the increase of the hematocrit and also decreases with the increasing values of the magnetic field gradient.The variation of axial velocities profiles
). It is clear from the figure that the flow rate decreases slowly with the increase of the hematocrit and also decreases with the increasing values of the magnetic field gradient.The variation of axial velocities profiles 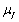 and
and 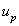 for both phase (plasma and erythrocyte ) with radial axis (r) for different values of hematocrit (
for both phase (plasma and erythrocyte ) with radial axis (r) for different values of hematocrit (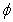 ) and permeability parameter( K=1) are plotted in fig. 5 and 7.It has been observed that the
) and permeability parameter( K=1) are plotted in fig. 5 and 7.It has been observed that the 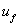 and
and 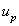 decreases with the increase of the hematocrit (
decreases with the increase of the hematocrit (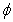 ) for constant magnetic field gradient (
) for constant magnetic field gradient (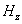 ) and the other parameters are keep constant.The effect of hematocrit of blood (
) and the other parameters are keep constant.The effect of hematocrit of blood (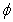 ) on the velocity is relatively small near the wall.It may be due to the red cell’s tendency to accumulate near the tube axis.
) on the velocity is relatively small near the wall.It may be due to the red cell’s tendency to accumulate near the tube axis.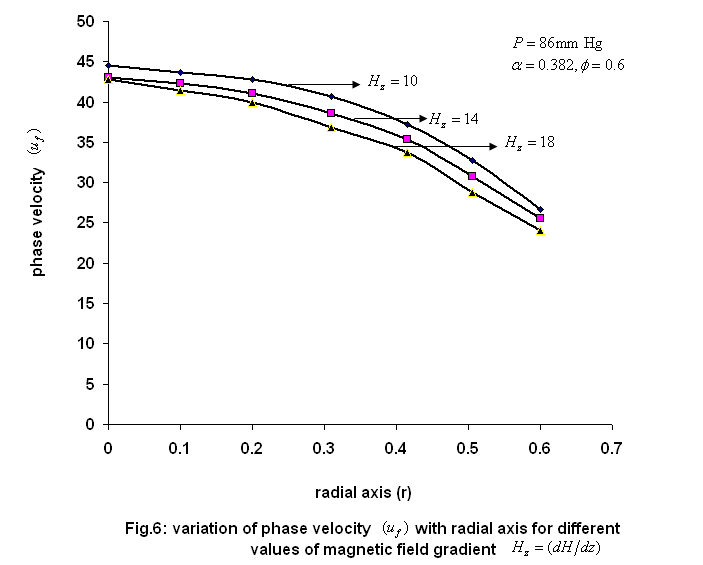 | Figure 6. variation of phase velocity ( )with radial axis for different values of magmetic field gradient )with radial axis for different values of magmetic field gradient  |
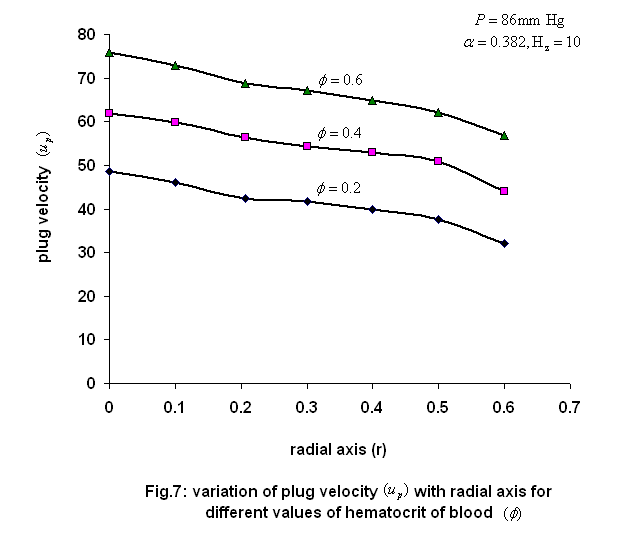 | Figure 7. variation of plug velocity (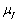 )with radial axis for different values of hematocrit of blood ( )with radial axis for different values of hematocrit of blood (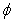 ),K=2.0 ),K=2.0 |
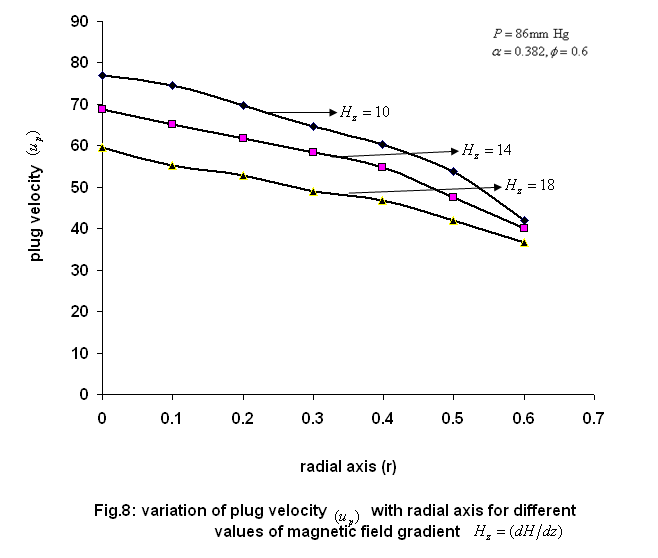 | Figure 8. variation of plug velocity (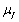 )with radial axis for different values of magmetic field gradient )with radial axis for different values of magmetic field gradient 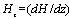 |
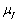 and
and 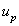 for both phases (plasma and erythrocyte ) with radial axis (r) for different values of magnetic field gradient (
for both phases (plasma and erythrocyte ) with radial axis (r) for different values of magnetic field gradient (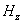 )and permeability parameter(K=1) .It is clear from the figure that
)and permeability parameter(K=1) .It is clear from the figure that 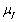 and
and 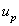 decrease with increase of the magnetic field gradient.Thus ,it is of important to note that though the suspended fluid is non magnetic the magnetic field gradient influences its velocity. All these results of the present study have been compared with already existing results obtained in the theoretical study of[2],[13] and[21].
decrease with increase of the magnetic field gradient.Thus ,it is of important to note that though the suspended fluid is non magnetic the magnetic field gradient influences its velocity. All these results of the present study have been compared with already existing results obtained in the theoretical study of[2],[13] and[21].5. Conclusions
- In the current study of a mathematical model of blood flow in the blood vessels in presence of magnetic field with effects of porous is investigated. We hope that our investigation may be helpful for the medical practitioners and other persons in the area of bio fluid dynamics to understand the flow of blood in the presence of porous effects. The results derived may be useful for hypertension patients through magnetic therapy. It is clear from the above discussion that magnetic field affects largely on the axial flow velocities of blood and on the effective viscosity.So,by taking appropriate values of magnetic field we may regulate the axial velocities and effective viscosity.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML