Sameena Saba
Karamat Husain Muslim Girls P.G. College Lucknow
Correspondence to: Sameena Saba , Karamat Husain Muslim Girls P.G. College Lucknow.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A generalization of sixth order and third order mock theta functions is given and shown that these generalized functions belong to the class of 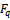 -functions. Multibasic expansion and q-integral representation of these generalized functions is also given.
-functions. Multibasic expansion and q-integral representation of these generalized functions is also given.
Keywords:
Basic Hypergeometric Series, Mock Theta Functions, q-Integral, Multibasic Expansions
Cite this paper:
Sameena Saba , "A Study of a Generalization of Ramanujan’s Third Order and Sixth Order Mock Theta Functions", Applied Mathematics, Vol. 2 No. 5, 2012, pp. 157-165. doi: 10.5923/j.am.20120205.02.
1. Introduction
S. Ramanujan in his last letter to G.H. Hardy[9, pp 354-355] introduced seventeen functions whom he called mock theta functions, as they were not theta functions. He stated two conditions for a function to be a mock theta function:(0) For every root of unity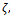 there is a θ-function
there is a θ-function 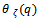 such that the difference
such that the difference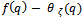 is bounded as
is bounded as 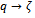 radially.(1) There is no single θ-function which works for all
radially.(1) There is no single θ-function which works for all 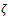 i.e., for every θ-function
i.e., for every θ-function 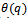 there is some root of unity
there is some root of unity 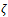 for which difference
for which difference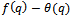 is unbounded as
is unbounded as 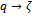 radially.Of the seventeen mock theta functions, four were of third order, ten of fifth order in two groups with five functions in each group and three of seventh order. Ramanujan did not specify what he meant by the order of a mock theta function. Later Watson[15] added three more third order mock theta functions, making the four third order mock theta functions to seven.G.E. Andrews[1] while visiting Trinity College Cambridge University discovered some notebooks of Ramanujan, and called it the “Lost” Notebook. In the Notebook Andrews found seven more mock theta functions and some identities and Andrews and Hickerson[2] called them of sixth order. The sixth order mock theta functions of Ramanujan are
radially.Of the seventeen mock theta functions, four were of third order, ten of fifth order in two groups with five functions in each group and three of seventh order. Ramanujan did not specify what he meant by the order of a mock theta function. Later Watson[15] added three more third order mock theta functions, making the four third order mock theta functions to seven.G.E. Andrews[1] while visiting Trinity College Cambridge University discovered some notebooks of Ramanujan, and called it the “Lost” Notebook. In the Notebook Andrews found seven more mock theta functions and some identities and Andrews and Hickerson[2] called them of sixth order. The sixth order mock theta functions of Ramanujan are 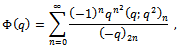
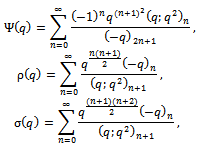 2000 Mathematics Subject Classification.33D15Key words and phrases. Basic Hypergeometric series, mock theta functions, q-integral, multibasic expansions.
2000 Mathematics Subject Classification.33D15Key words and phrases. Basic Hypergeometric series, mock theta functions, q-integral, multibasic expansions. 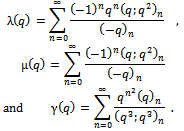 The third order mock theta functions of Ramanujan are
The third order mock theta functions of Ramanujan are 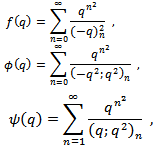
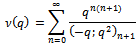 We give a generalization of the sixth order and the third order mock theta functions. The generalized sixth order mock theta functions are
We give a generalization of the sixth order and the third order mock theta functions. The generalized sixth order mock theta functions are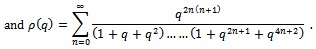
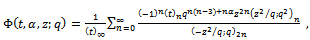 | (1.1) |
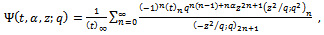 | (1.2) |
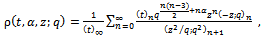 | (1.3) |
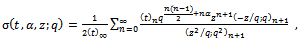 | (1.4) |
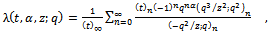 | (1.5) |
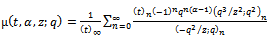 | (1.6) |
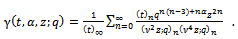 | (1.7) |
For 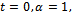 we have the generalized functions of Choi[4]. For
we have the generalized functions of Choi[4]. For 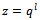 and using induction, these functions satisfy the Ramanujan’s requirement for a mock theta function.The generalized third order mock theta functions are
and using induction, these functions satisfy the Ramanujan’s requirement for a mock theta function.The generalized third order mock theta functions are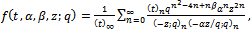 | (1.8) |
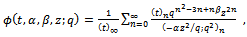 | (1.9) |
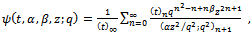 | (1.10) |
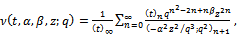 | (1.11) |
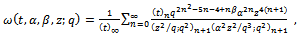 | (1.12) |
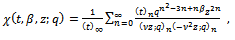 | (1.13) |
and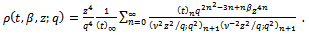 | (1.14) |
where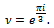 For
For 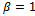 and
and 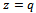 we have generalized five third order mock theta functions namely
we have generalized five third order mock theta functions namely 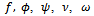 of Andrews[1]. For
of Andrews[1]. For 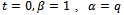 and
and 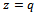 the generalized functions
the generalized functions 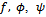 and
and 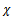 reduce to the third order mock theta functions of Ramanujan and
reduce to the third order mock theta functions of Ramanujan and 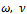 and ρ to the third order mock theta functions of Watson[15].In this study we will show that these generalized functions are
and ρ to the third order mock theta functions of Watson[15].In this study we will show that these generalized functions are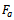 -functions. This is done in section 3.Using the difference equation we derive relations between generalized sixth order mock theta functions and relation between generalized third order mock theta functions. This we do in section 4. In section 5 we give a q-integral representation and in section 6, we give multibasic expansion for these generalized functions.
-functions. This is done in section 3.Using the difference equation we derive relations between generalized sixth order mock theta functions and relation between generalized third order mock theta functions. This we do in section 4. In section 5 we give a q-integral representation and in section 6, we give multibasic expansion for these generalized functions.
2. Notations
We shall use the following usual basic hypergeometric notations: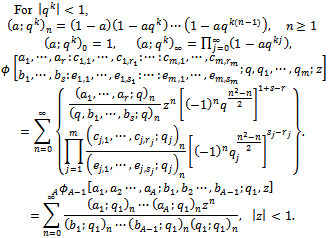
3. The Generalized Functions are 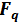 -Functions
-Functions
We show these generalized functions are 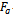 - functions.Theorem 1The generalized functions
- functions.Theorem 1The generalized functions 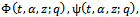
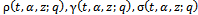 and the generalized functions
and the generalized functions 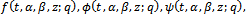
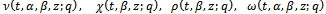 are
are 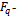 functions.ProofsWe shall give the proof for
functions.ProofsWe shall give the proof for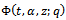 only. The proofs for the other functions are similar, hence omitted.Applying the difference operator
only. The proofs for the other functions are similar, hence omitted.Applying the difference operator 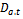 to
to 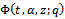 we have
we have 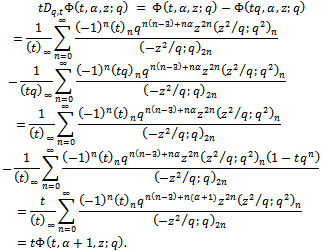 So
So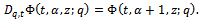 Hence
Hence 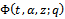 is a
is a 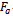 - function.As stated earlier the proofs for other functions are similar, so omitted.
- function.As stated earlier the proofs for other functions are similar, so omitted.
4. Relations between the Generalized Functions of Sixth Order Mock Theta Functions and Relations between Generalized Functions of Third Order Mock Theta Functions
Theorem 2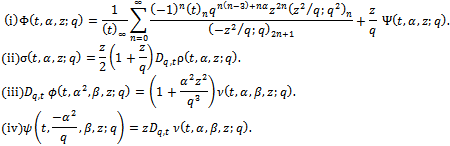 Proof of (i)which proves Theorem 2 (i).Proof of (ii)
Proof of (i)which proves Theorem 2 (i).Proof of (ii) which proves Theorem 2 (ii).Proof of (iii)Writing
which proves Theorem 2 (ii).Proof of (iii)Writing  for α in
for α in 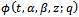 , we have
, we have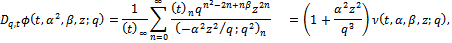 which proves Theorem 2 (iii).Proof of (iv)Writing
which proves Theorem 2 (iii).Proof of (iv)Writing 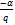 for α and then
for α and then 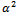 for α in
for α in 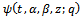 in (1.8), we have
in (1.8), we have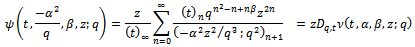 which proves Theorem 2 (iv).
which proves Theorem 2 (iv).
5. q-Integral Representation for the Generalized Functions of Sixth and Third Order Mock Theta Functions
The q-integral was defined by Thomae and Jackson[7, p. 19] as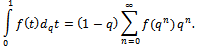 We now give the q-integral representation for the generalized sixth order mock theta functions and also for generalized third order mock theta functions. Theorem 3(a)
We now give the q-integral representation for the generalized sixth order mock theta functions and also for generalized third order mock theta functions. Theorem 3(a)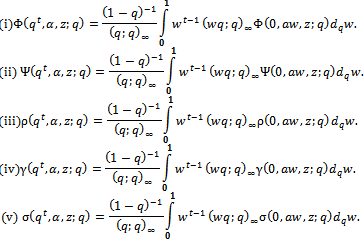 ProofWe shall give the detailed proof for
ProofWe shall give the detailed proof for 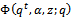 The proofs for the other functions are similar, so omitted.Limiting case of q-beta integral[7, p. 19 (1.11.7)] is
The proofs for the other functions are similar, so omitted.Limiting case of q-beta integral[7, p. 19 (1.11.7)] is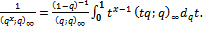 | (5.1) |
Now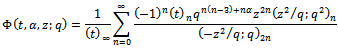 Replacing t by
Replacing t by 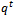 and
and 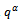 by a, we have
by a, we have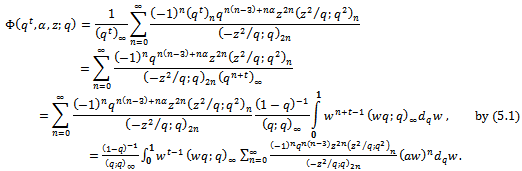 | (5.2) |
But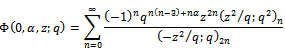 and since
and since 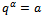 ,
,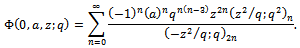 Hence
Hence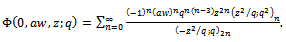 | (5.3) |
by using (5.3), (5.2) can be written as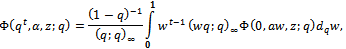 which proves (i). The proofs for all other functions are similar.Theorem 3(b)The q-integral representation for the generalized third order mock theta functions:
which proves (i). The proofs for all other functions are similar.Theorem 3(b)The q-integral representation for the generalized third order mock theta functions: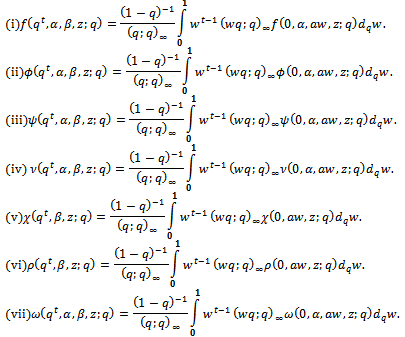 ProofThe proofs are similar to given above for
ProofThe proofs are similar to given above for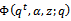 , so the Theorem 3(b) follows.
, so the Theorem 3(b) follows.
6. Multibasic Expansions of Generalized Functions of Sixth and Third Order Mock Theta Functions
Using the summation formula[7, (3.6.7), p. 71] and[8, Lemma 10, p. 57], we have the multibasic expansion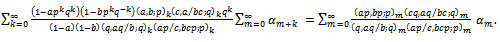 | (6.1) |
Corollary 1Letting 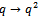 and
and 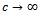 in (6.1) we have
in (6.1) we have | (6.2) |
Corollary 2Letting 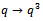 and
and 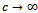 in (6.1) we have
in (6.1) we have 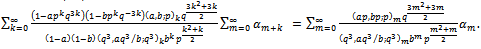 | (6.3) |
Corollary 3Letting 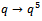 and
and 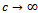 in (6.1) we have
in (6.1) we have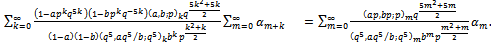 | (6.4) |
In the following Theorem we now give multibasic expansions for generalized functions of sixth order mock theta functions and third order mock theta functions. We give detailed proof for 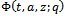 and for other functions we write only the specialized parameters.Theorem 4(a)The expansions for generalized functions of sixth order mock theta functions.
and for other functions we write only the specialized parameters.Theorem 4(a)The expansions for generalized functions of sixth order mock theta functions.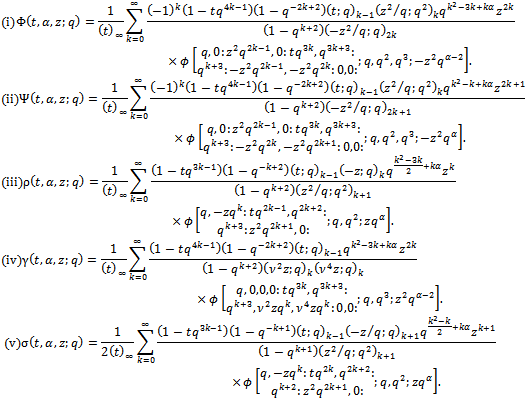 Proof of (i)
Proof of (i)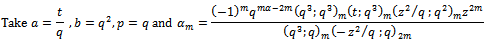 in (6.3) to get
in (6.3) to get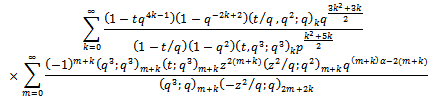
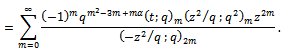 The right hand side of (6.5) is equal to
The right hand side of (6.5) is equal to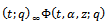 The left hand side of (6.5) is equal to
The left hand side of (6.5) is equal to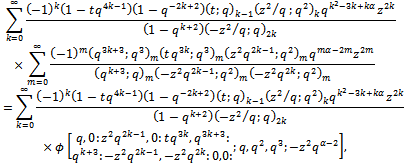 which proves Theorem 4(a)(i).Proof of (ii)
which proves Theorem 4(a)(i).Proof of (ii)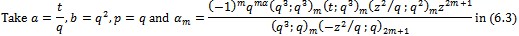 Proof of (iii)
Proof of (iii)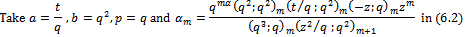 Proof of (iv)
Proof of (iv)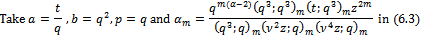 Proof of (v)
Proof of (v)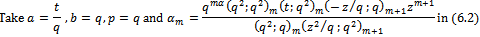 Theorem 4(b)The expansions for generalized functions of mock theta functions of third order.
Theorem 4(b)The expansions for generalized functions of mock theta functions of third order.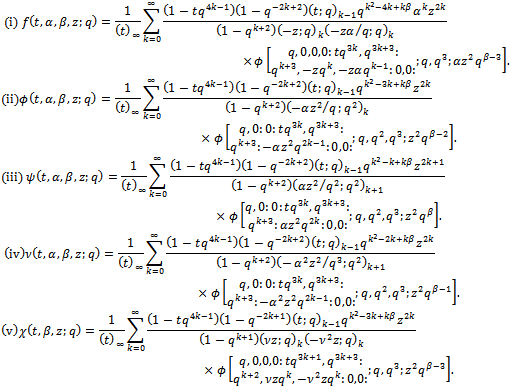
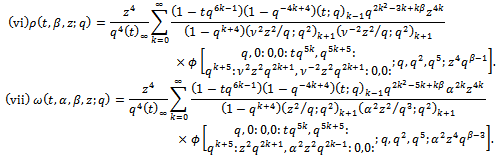 Proof of (i)
Proof of (i)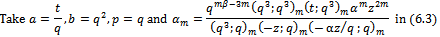 Proof of (ii)
Proof of (ii)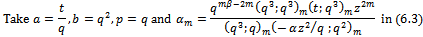 Proof of (iii)
Proof of (iii)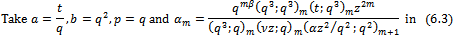 Proof of (iv)
Proof of (iv)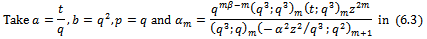 Proof of (v)
Proof of (v)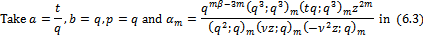 Proof of (vi)
Proof of (vi)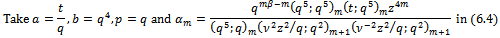 Proof of (vii)
Proof of (vii)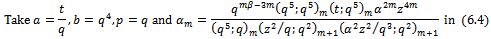
7. Conclusions
Mock theta functions are mysterious functions. These investigations will be helpful in understanding more about these functions. Being shown that they belong to the class of 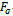 -functions more properties can be established and relations between these mock theta functions can also be derived.
-functions more properties can be established and relations between these mock theta functions can also be derived.
ACKNOWLEDGEMENTS
I am thankful to Dr. Bhaskar Srivastava for his help and guidance.
References
| [1] | G.E. Andrews, On basic hypergeometric mock theta functions and partitions (1), Quart. J. Math. 17 (1966) 64-80. |
| [2] | G.E. Andrews and D. Hickerson, Ramanujan’s ‘Lost’ Notebook-VII: The sixth order mock theta functions, Adv. in Math. 89 (1991) 60-105. |
| [3] | G.E. Andrews and B.C. Berndt, Ramanujan’s ‘Lost’ Notebook Part I, Springer New York (2005). |
| [4] | G.E. Andrews and B.C. Berndt, Ramanujan’s ‘Lost’ Notebook Part II, Springer New York (2009). |
| [5] | Y.S. Choi, The Basic Bilateral Hypergeometric Series and the Mock Theta Functions, Ramanujan J. 24 (2011) 345-386. |
| [6] | Y.S. Choi, Tenth order mock theta functions in Ramanujan’s lost notebook IV, Trans. Amer. Math.Soc. 354 (2002) 705-733. |
| [7] | G. Gasper and M. Rahman, Basic Hypergeometric Series, Cambridge University Press, Cambridge, (1990). |
| [8] | E.D. Rainville, Special Function, Chelsea Publishing Company, Bronx, New York (1960). |
| [9] | S. Ramanujan, Collected Papers, Cambridge University Press, 1972, reprinted Chelsea, New York, (1962). |
| [10] | C.D. Savage and A.J. Yee, Euler’s partition theorem and the combinatorics of -sequences, J. Combin. Thy. Ser. A 115 (2008) 967-996. |
| [11] | Bhaskar Srivastava, Ramanujan’s fifth order and tenth order mock theta functions- A generalization (Communicated). |
| [12] | B. Srivastava, A Comprehensive study of second order mock theta functions, Bull. Korean Math. Soc. 42 No. 4 (2005) 889-900. |
| [13] | B. Srivastava, A Study of -functions connected with Ramanujan tenth order Mock theta functions, Math. J. Okayam Univ. 46 (2004) 131-139. |
| [14] | Bhaskar Srivastava, On a generalization of Ramanujan’s seventh order mock theta functions (Communicated). |
| [15] | G.N. Watson, The final problem: an account of the mock theta functions, J. London Math. Soc. 11 (1936) 55-80. |

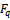 -functions. Multibasic expansion and q-integral representation of these generalized functions is also given.
-functions. Multibasic expansion and q-integral representation of these generalized functions is also given.
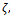 there is a θ-function
there is a θ-function 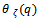 such that the difference
such that the difference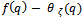 is bounded as
is bounded as 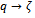 radially.(1) There is no single θ-function which works for all
radially.(1) There is no single θ-function which works for all 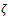 i.e., for every θ-function
i.e., for every θ-function 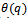 there is some root of unity
there is some root of unity 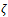 for which difference
for which difference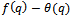 is unbounded as
is unbounded as 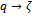 radially.Of the seventeen mock theta functions, four were of third order, ten of fifth order in two groups with five functions in each group and three of seventh order. Ramanujan did not specify what he meant by the order of a mock theta function. Later Watson[15] added three more third order mock theta functions, making the four third order mock theta functions to seven.G.E. Andrews[1] while visiting Trinity College Cambridge University discovered some notebooks of Ramanujan, and called it the “Lost” Notebook. In the Notebook Andrews found seven more mock theta functions and some identities and Andrews and Hickerson[2] called them of sixth order. The sixth order mock theta functions of Ramanujan are
radially.Of the seventeen mock theta functions, four were of third order, ten of fifth order in two groups with five functions in each group and three of seventh order. Ramanujan did not specify what he meant by the order of a mock theta function. Later Watson[15] added three more third order mock theta functions, making the four third order mock theta functions to seven.G.E. Andrews[1] while visiting Trinity College Cambridge University discovered some notebooks of Ramanujan, and called it the “Lost” Notebook. In the Notebook Andrews found seven more mock theta functions and some identities and Andrews and Hickerson[2] called them of sixth order. The sixth order mock theta functions of Ramanujan are 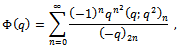
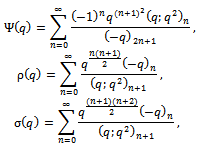 2000 Mathematics Subject Classification.33D15Key words and phrases. Basic Hypergeometric series, mock theta functions, q-integral, multibasic expansions.
2000 Mathematics Subject Classification.33D15Key words and phrases. Basic Hypergeometric series, mock theta functions, q-integral, multibasic expansions. 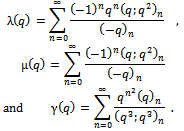 The third order mock theta functions of Ramanujan are
The third order mock theta functions of Ramanujan are 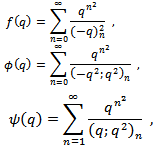
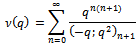 We give a generalization of the sixth order and the third order mock theta functions. The generalized sixth order mock theta functions are
We give a generalization of the sixth order and the third order mock theta functions. The generalized sixth order mock theta functions are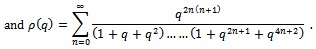
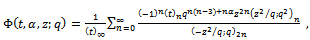
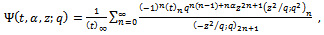
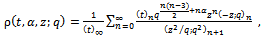
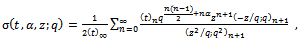
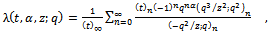
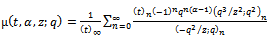
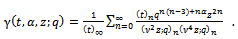
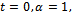 we have the generalized functions of Choi[4]. For
we have the generalized functions of Choi[4]. For 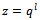 and using induction, these functions satisfy the Ramanujan’s requirement for a mock theta function.The generalized third order mock theta functions are
and using induction, these functions satisfy the Ramanujan’s requirement for a mock theta function.The generalized third order mock theta functions are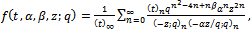
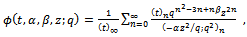
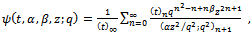
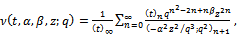
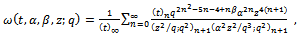
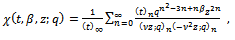
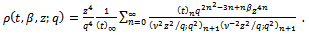
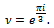 For
For 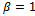 and
and 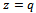 we have generalized five third order mock theta functions namely
we have generalized five third order mock theta functions namely 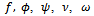 of Andrews[1]. For
of Andrews[1]. For 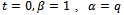 and
and 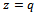 the generalized functions
the generalized functions 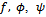 and
and 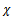 reduce to the third order mock theta functions of Ramanujan and
reduce to the third order mock theta functions of Ramanujan and 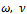 and ρ to the third order mock theta functions of Watson[15].In this study we will show that these generalized functions are
and ρ to the third order mock theta functions of Watson[15].In this study we will show that these generalized functions are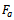 -functions. This is done in section 3.Using the difference equation we derive relations between generalized sixth order mock theta functions and relation between generalized third order mock theta functions. This we do in section 4. In section 5 we give a q-integral representation and in section 6, we give multibasic expansion for these generalized functions.
-functions. This is done in section 3.Using the difference equation we derive relations between generalized sixth order mock theta functions and relation between generalized third order mock theta functions. This we do in section 4. In section 5 we give a q-integral representation and in section 6, we give multibasic expansion for these generalized functions.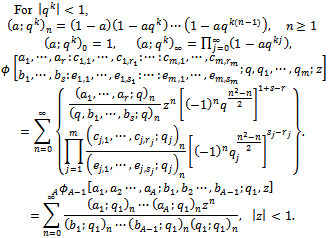
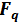 -Functions
-Functions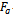 - functions.Theorem 1The generalized functions
- functions.Theorem 1The generalized functions 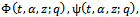
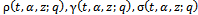 and the generalized functions
and the generalized functions 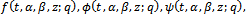
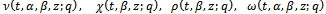 are
are 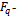 functions.ProofsWe shall give the proof for
functions.ProofsWe shall give the proof for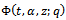 only. The proofs for the other functions are similar, hence omitted.Applying the difference operator
only. The proofs for the other functions are similar, hence omitted.Applying the difference operator 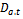 to
to 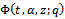 we have
we have 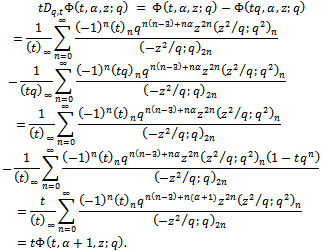 So
So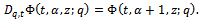 Hence
Hence 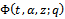 is a
is a  - function.As stated earlier the proofs for other functions are similar, so omitted.
- function.As stated earlier the proofs for other functions are similar, so omitted.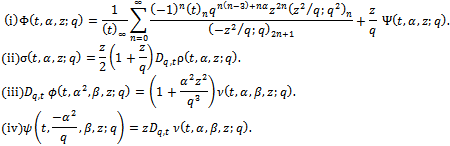 Proof of (i)which proves Theorem 2 (i).Proof of (ii)
Proof of (i)which proves Theorem 2 (i).Proof of (ii)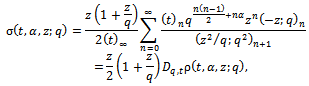 which proves Theorem 2 (ii).Proof of (iii)Writing
which proves Theorem 2 (ii).Proof of (iii)Writing 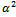 for α in
for α in 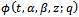 , we have
, we have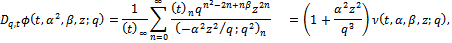 which proves Theorem 2 (iii).Proof of (iv)Writing
which proves Theorem 2 (iii).Proof of (iv)Writing 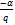 for α and then
for α and then 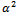 for α in
for α in 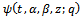 in (1.8), we have
in (1.8), we have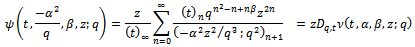 which proves Theorem 2 (iv).
which proves Theorem 2 (iv).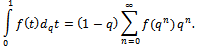 We now give the q-integral representation for the generalized sixth order mock theta functions and also for generalized third order mock theta functions. Theorem 3(a)
We now give the q-integral representation for the generalized sixth order mock theta functions and also for generalized third order mock theta functions. Theorem 3(a)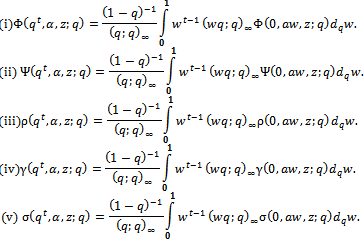 ProofWe shall give the detailed proof for
ProofWe shall give the detailed proof for  The proofs for the other functions are similar, so omitted.Limiting case of q-beta integral[7, p. 19 (1.11.7)] is
The proofs for the other functions are similar, so omitted.Limiting case of q-beta integral[7, p. 19 (1.11.7)] is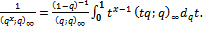
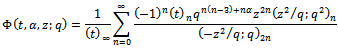 Replacing t by
Replacing t by  and
and  by a, we have
by a, we have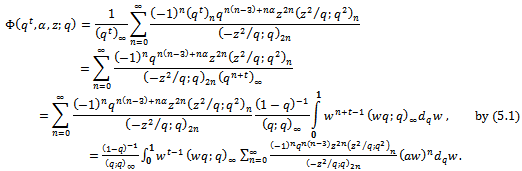
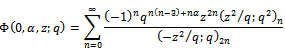 and since
and since 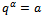 ,
,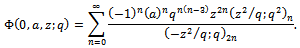 Hence
Hence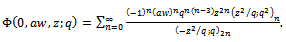
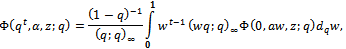 which proves (i). The proofs for all other functions are similar.Theorem 3(b)The q-integral representation for the generalized third order mock theta functions:
which proves (i). The proofs for all other functions are similar.Theorem 3(b)The q-integral representation for the generalized third order mock theta functions: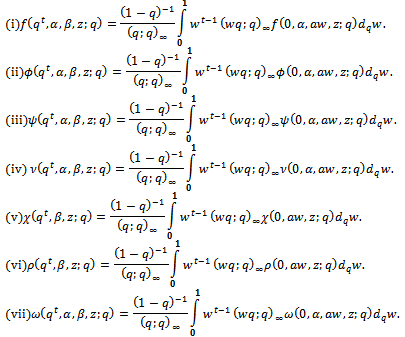 ProofThe proofs are similar to given above for
ProofThe proofs are similar to given above for , so the Theorem 3(b) follows.
, so the Theorem 3(b) follows.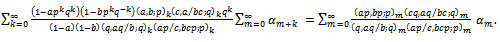
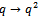 and
and 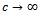 in (6.1) we have
in (6.1) we have
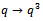 and
and  in (6.1) we have
in (6.1) we have 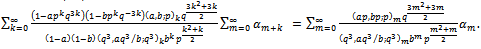
 and
and  in (6.1) we have
in (6.1) we have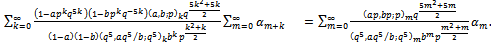
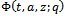 and for other functions we write only the specialized parameters.Theorem 4(a)The expansions for generalized functions of sixth order mock theta functions.
and for other functions we write only the specialized parameters.Theorem 4(a)The expansions for generalized functions of sixth order mock theta functions.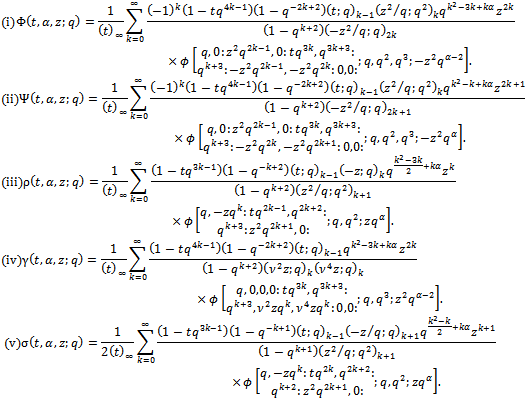 Proof of (i)
Proof of (i)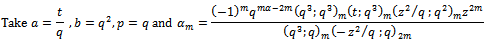 in (6.3) to get
in (6.3) to get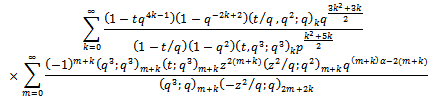
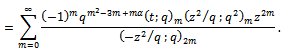 The right hand side of (6.5) is equal to
The right hand side of (6.5) is equal to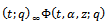 The left hand side of (6.5) is equal to
The left hand side of (6.5) is equal to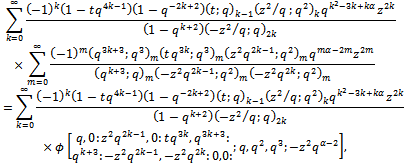 which proves Theorem 4(a)(i).Proof of (ii)
which proves Theorem 4(a)(i).Proof of (ii)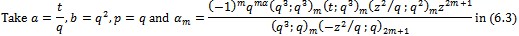 Proof of (iii)
Proof of (iii)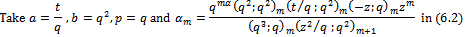 Proof of (iv)
Proof of (iv)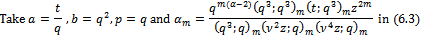 Proof of (v)
Proof of (v)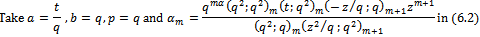 Theorem 4(b)The expansions for generalized functions of mock theta functions of third order.
Theorem 4(b)The expansions for generalized functions of mock theta functions of third order.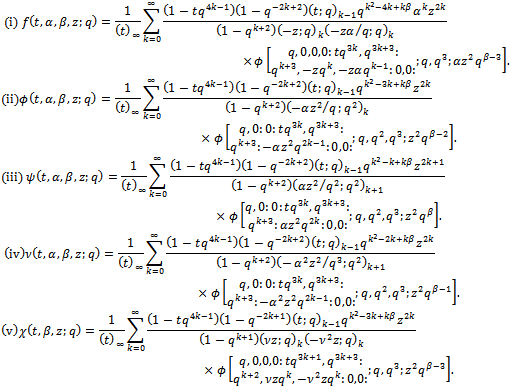
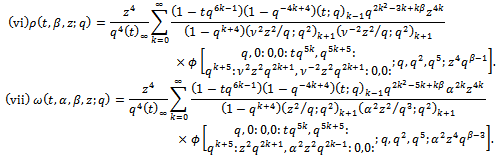 Proof of (i)
Proof of (i)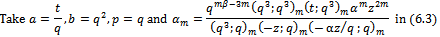 Proof of (ii)
Proof of (ii)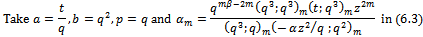 Proof of (iii)
Proof of (iii)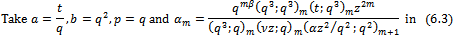 Proof of (iv)
Proof of (iv)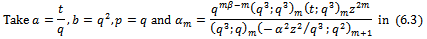 Proof of (v)
Proof of (v)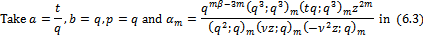 Proof of (vi)
Proof of (vi)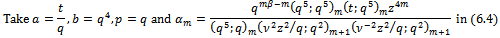 Proof of (vii)
Proof of (vii)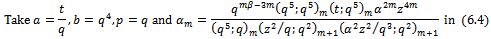
 -functions more properties can be established and relations between these mock theta functions can also be derived.
-functions more properties can be established and relations between these mock theta functions can also be derived. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML