-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(4): 146-151
doi:10.5923/j.am.20120204.09
Partial New Mock Theta Functions
Abstract
Reference
Full-Text PDF
Full-text HTMLBhaskar Srivastava
Department of Mathematics and Astronomy, Lucknow University, Lucknow, India
Correspondence to: Bhaskar Srivastava, Department of Mathematics and Astronomy, Lucknow University, Lucknow, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
By using a simple identity of mine, I have proved sixty identities connecting the mock theta functions of Ramanujan with mock theta functions recently generated by Andrews and Bringmann et al, by taking their partial sums.
Keywords: Mock Theta Function, Partial Mock Theta Function, Q-Hypergeometric Series
Cite this paper: Bhaskar Srivastava, Partial New Mock Theta Functions, Applied Mathematics, Vol. 2 No. 4, 2012, pp. 146-151. doi: 10.5923/j.am.20120204.09.
Article Outline
- 5.2. Relations of Mock Theta Functions of Andrews with Third Order Mock Theta Functions of Ramanujan
- 5.3. Relations of Mock Theta Functions of Andrews with Fifth Order Mock Theta Functions of Ramanujan
- 5.4. Relations of Mock Theta Functions of Andrews with Sixth Order Mock Theta Functions of Ramanujan
1. Introduction
- In his last letter to G.H. Hardy[14], Ramanujan wrote “I discovered very interesting functions recently which I call mock theta functions”. He also listed seventeen functions—four of order three, two groups five in each group of order five and three of order seven. He did not explain what he meant by “order” of the mock theta functions. Later Watson gave three more mock theta functions of order three.Andrews while visiting Cambridge University found notebooks of Ramanujan and called them “lost” notebooks. The “lost” notebooks contain six mock theta functions and Andrews and Hickerson[7] called them of order six. The “lost” notebook also contains eight identities for the mock theta functions and Choi[10] called these mock theta functions of order ten.Gordon and McIntosh[13] gave eight mock theta functions and called them of order eight, though four of them are of lesser order. Hikami also gave a mock theta function and called it of order two.Recently Andrews in his paper[6] generated some mock theta functions and found four of them interesting. Bringmann, Hikami and Lovejoy found two more mock theta functions. We have made comprehensive study of these functions in [16],[17] and also their bilateral form in[18].In some of Ramanujan’s unpublished work, now published as “lost” notebook, a number of identities and expansion formulas for partial sums of theta functions are mentioned without proof. A study of these partial sums, identities and expansions has been made by Andrews and he wrote that some of these partial theta functions identities have interesting number theoretic interpretations. These observations motivated me to study the partial mock theta functions. The definition of a partial mock theta functions is that we take the partial sum of the infinite series representing these functions. Thus for mock theta function
,
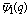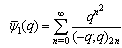the partial mock theta function will be defined and denoted as
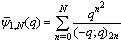Moreover, by taking the partial sum, the additional advantage is that convergence of the series is not a restraint.In this paper we use a simple summation identity and using this identity we connect the mock theta functions of Andrews among themselves and the mock theta functions of Bringmann et al among themselves. Further we show the relationship between mock theta functions of Andrews with the third, fifth, sixth and tenth order mock theta function of Ramanujan and with eighth order mock theta functions of Gordon and McIntosh.The mock theta functions of Andrews [6]: 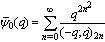| (1.1) |
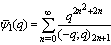 | (1.2) |
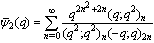 | (1.3) |
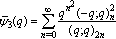 | (1.4) |
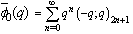 | (1.5) |
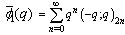 | (1.6) |
2. Basic Results
- The following q- notations have been usedFor
,
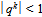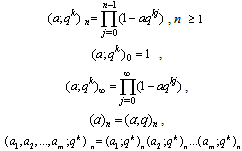A generalized basic hypergeometric series with base is defined as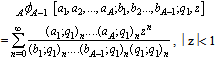
3. Definitions of Mock Theta Functions
- Third order mock theta functions of Ramanujan:
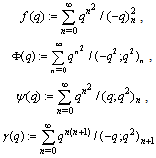Fifth order mock theta functions of Ramanujan: 
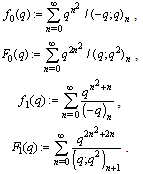Sixth order mock theta functions of Ramanujan :
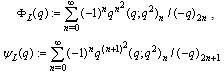To distinguish these functions from the others in notation, we have put a suffix L in their symbols.Seventh order mock theta functions of Ramanujan:
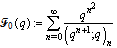Eighth order mock theta functions of Gordon and McIntosh: 
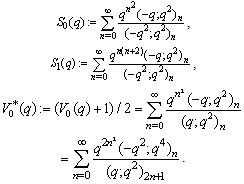Tenth order mock theta functions of Ramanujan: 
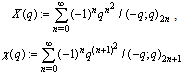Second order mock theta function 
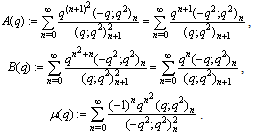Alternative definitions of second order mock theta functions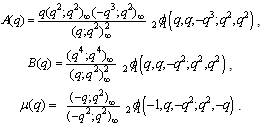
4. Main Summation Theorem
- We give a proof of the following identityTheorem
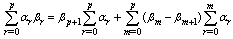 | (4.1) |
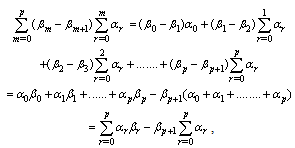which proves the theorem.5. Relations of Partial New Mock Theta Functions with Mock Theta Functions of Ramanujan
5.1. Relations among Partial Mock Theta Functions of Andrews and Partial Mock Theta Functions of Bringmann et al
- We give relations between partial mock theta functions of Andrews and partial mock theta functions of Bringmann et al. In the limit we have the mock theta functions expressed as a series in partial mock theta functions.By definition
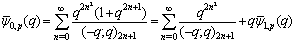 | (5.1) |
, 
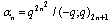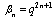in (4.1), we have 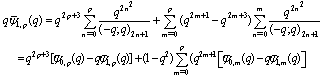| (5.2) |
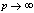in (5.2), we have 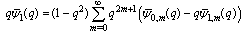| (5.3) |
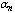and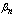 
will be indicated in parenthesis.  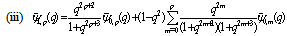| (5.4) |
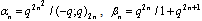in (4.1)) 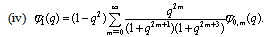| (5.5) |
in (5.4))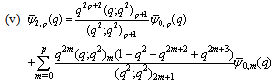 | (5.6) |
,
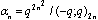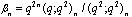in (4.1)) 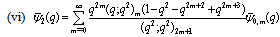| (5.7) |
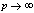in (5.6)) 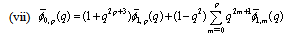| (5.8) |
,
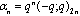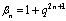in (4.1)) 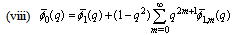| (5.9) |
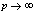in (5.8))5.2. Relations of Mock Theta Functions of Andrews with Third Order Mock Theta Functions of Ramanujan
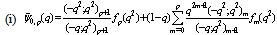 | (5.10) |
,
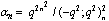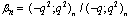in (4.1)) 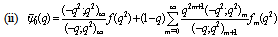| (5.11) |
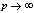in (5.10)) 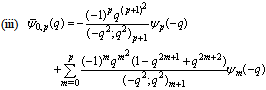| (5.12) |
,
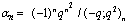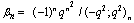in (4.1)) 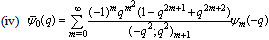| (5.13) |
in (5.12))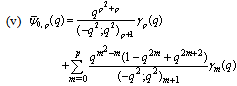 | (5.14) |
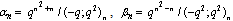in (4.1)) 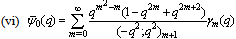| (5.15) |
in (5.14))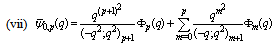 | (5.16) |
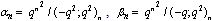in (4.1)) 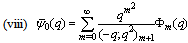| (5.17) |
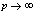in (5.16)) 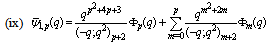| (5.18) |
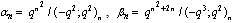in (4.1)) 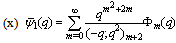| (5.19) |
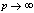in (5.18))5.3. Relations of Mock Theta Functions of Andrews with Fifth Order Mock Theta Functions of Ramanujan
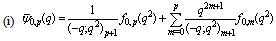 | (5.20) |
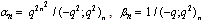in (4.1)) 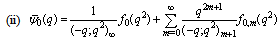| (5.21) |
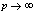in (5.20)) 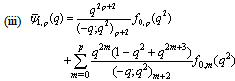| (5.22) |
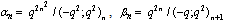in (4.1)) 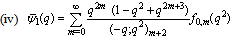| (5.23) |
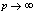in (5.22)) 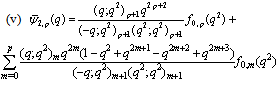| (5.24) |
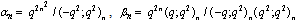in (4.1)) 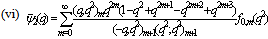| (5.25) |
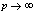in (5.24)) 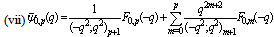| (5.26) |
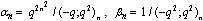in (4.1)) 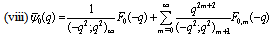| (5.27) |
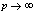in (5.26)) 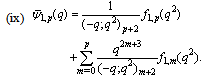| (5.28) |
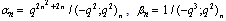in (4.1)) 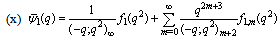| (5.29) |
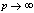in (5.28)) 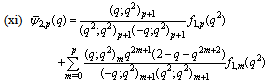| (5.30) |
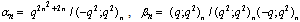in (4.1)) 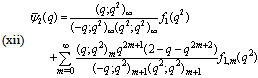| (5.31) |
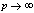in (5.30)) 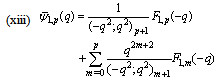| (5.32) |
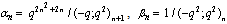in (4.1)) 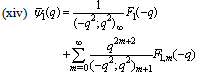| (5.33) |
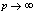in (5.32))5.4. Relations of Mock Theta Functions of Andrews with Sixth Order Mock Theta Functions of Ramanujan
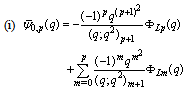 | (5.34) |
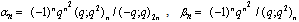in (4.1)) 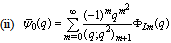| (5.35) |
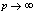in (5.34)) 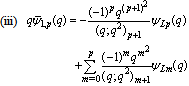| (5.36) |
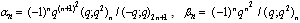in (4.1)) 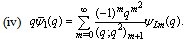| (5.37) |
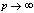in (5.36))5.5. Relations of Mock Theta Functions of Andrews with Seventh Order Mock Theta Functions of Ramanujan
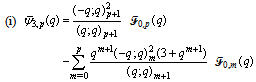 | (5.38) |
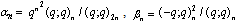in (4.1)) 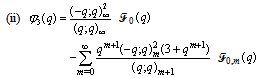| (5.39) |
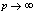in (5.38))5.6. Relations of Mock Theta Functions of Andrews with Eighth Order Mock Theta Functions of Gordon and McIntosh
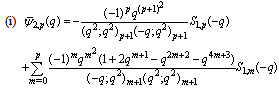 | (5.40) |
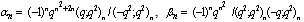in (4.1)) 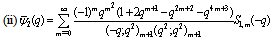| (5.41) |
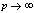in (5.40)) 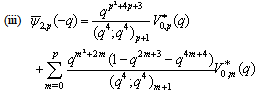| (5.42) |
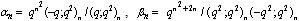in (4.1)) 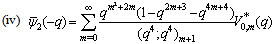| (5.43) |
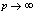in (5.42)) 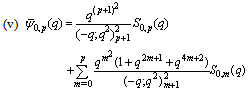| (5.44) |
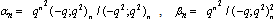in (4.1)) 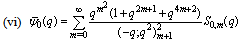| (5.45) |
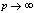in (5.44)) 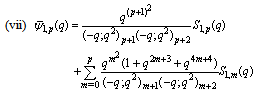| (5.46) |
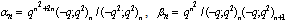in (4.1)) 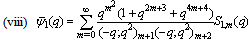| (5.47) |
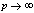in (5.46))5.7. Relations of Mock Theta Functions of Andrews with Tenth Order Mock Theta Functions of Ramanujan
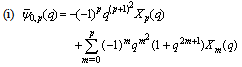 | (5.48) |
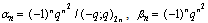in (4.1)) 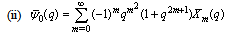| (5.49) |
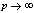in (5.48)) 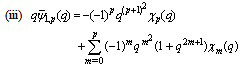| (5.50) |
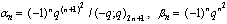in (4.1)) 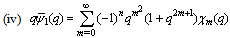| (5.51) |
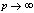in (5.50))5.8. Relations of Mock Theta Functions of Andrews and Mock Theta Functions of Bringmann et al with Second Order Mock Theta Functions
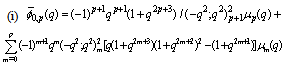 | (5.52) |
,
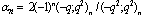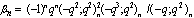in (4.1)) 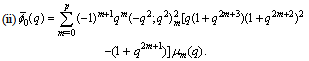| (5.53) |
in (5.52))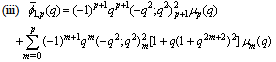 | (5.54) |
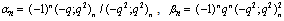in (4.1)) 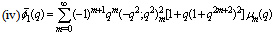| (5.55) |
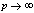in (5.54)) 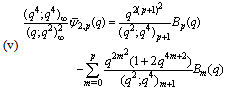| (5.56) |
,
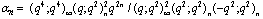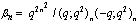in (4.1)) 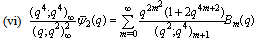| (5.57) |
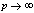in (5.56)) 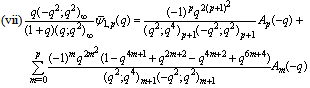| (5.58) |
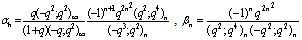in (4.1)) 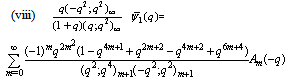| (5.59) |
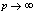in (5.58)) 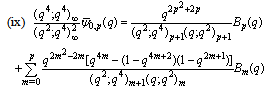| (5.60) |
,
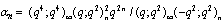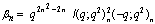in (4.1)) 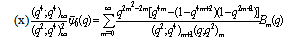| (5.61) |
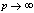in (5.60))6. Conclusions
- By the help of a simple summation formula identities connecting various partial mock theta functions are given. The consideration of partial sums of the mock theta functions is helpful as there is no constraint about convergence of the series. These partial identities may be helpful in giving number theoretic interpretations.