-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(4): 141-145
doi: 10.5923/j.am.20120204.08
On the Boundedness Properties of Solutions to Set Control Differential Equations
Nguyen Dinh Phu 1, Le Thanh Quang 1, Lam Quoc Dung 2
1Faculty of Mathematics and Computer Science,University of Science-VNU Ho Chi Minh City, Vietnam
2Faculty of Economics and Commerce, Hoa Sen University, Ho Chi Minh City, Vietnam
Correspondence to: Nguyen Dinh Phu , Faculty of Mathematics and Computer Science,University of Science-VNU Ho Chi Minh City, Vietnam.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The set-valued differential equations (SDEs) are important parts of the set-valued analysis theory. It was investigeted by professor Lakshmikantham V., and many other authors (see[1]-[6],[8]-[10]). Beside that, we have to studied the problems of existence, comparison and stability of set solutions to the set-valued control differential equations (SCDEs) (see[7],[11]-[16]). In this paper, we present the problems of boundedness for set solutions to the Set Control Differential Equations (SCDEs) by the Lyapunov-like functions and by admisible control- feedback.
Keywords: Set Differential Equations (SDEs), Set Control Differential Equations (SCDEs)
1. Introduction
- In the last 10 years, set-valued analysis is interesting with the new field of set differential equations (SDEs). There are many the authors are interesting in field of SDEs, for example, Lakshmikantham V., Gnana T., Kaleva O., Mohapatra R.,... Before we proceed to investigate our problems, let's note the following facts:In[5], Prof.V. Lakshmikantham and the other authors have studied the set differential equations (SDEs).In[13] and[16], the authors have considered the set control differential equations (SCDEs), that is SDEs with set controls:
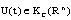 and have some important results on existence, stability.In[11] the author has given many kinds of feedback
and have some important results on existence, stability.In[11] the author has given many kinds of feedback 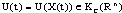 for problem of global controllability.In this paper, we present the boundedness of set solutions to SCDEs by the Liapunov-like functions and by feedback.This paper is organized as follows: in section 2, we recall some basic concepts and notations which are useful in next sections. In section 3 we present the boundedness properties of set solutions to SCDEs and in the last section, we give the conclusion and acknowledgements.
for problem of global controllability.In this paper, we present the boundedness of set solutions to SCDEs by the Liapunov-like functions and by feedback.This paper is organized as follows: in section 2, we recall some basic concepts and notations which are useful in next sections. In section 3 we present the boundedness properties of set solutions to SCDEs and in the last section, we give the conclusion and acknowledgements.2. Preliminaries
- In[5], Prof.V. Lakshmikantham and the other authors have studied the set differential equations (SDEs). In this work the authors have considered the Hausdorff metric space as followings:Let
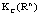 denote the collection of all nonempty convex subsets of
denote the collection of all nonempty convex subsets of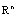 . Given
. Given 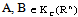 - the Hausdorff distance between A and B is defined by
- the Hausdorff distance between A and B is defined by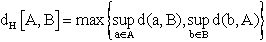 We define the magnitude of a nonempty subset of A
We define the magnitude of a nonempty subset of A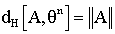 We define the magnitude of a nonempty subset of A:
We define the magnitude of a nonempty subset of A: 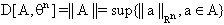 | (1) |
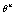 is the zero element of
is the zero element of 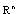 which is regarded as a one point set.
which is regarded as a one point set. 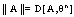 - norm in
- norm in 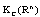 is finite when the supremum in (1) is attained with
is finite when the supremum in (1) is attained with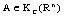 . The set
. The set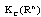 , with the metric D defined above, is a complete metric space. It has been proven that
, with the metric D defined above, is a complete metric space. It has been proven that 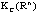 becomes a semilinear metric space which can be embedded as a complete cone into a corresponding Banach space, if it is equipped with the natural algebraic operations of addition and nonnegative scalar multiplication.Let
becomes a semilinear metric space which can be embedded as a complete cone into a corresponding Banach space, if it is equipped with the natural algebraic operations of addition and nonnegative scalar multiplication.Let 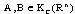 if there exists a set
if there exists a set 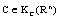 such that
such that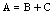 , then C is called the Hausdorff difference (the geometric difference) of the sets A and B and is denoted by the symbol A-B The mapping
, then C is called the Hausdorff difference (the geometric difference) of the sets A and B and is denoted by the symbol A-B The mapping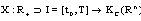 is said to have a Hukuhara derivative
is said to have a Hukuhara derivative 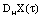 at a point
at a point 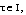 if
if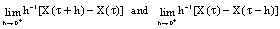 exist in the topology of
exist in the topology of 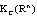 and are equal to
and are equal to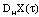 .By embedding
.By embedding 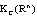 as a complete cone in a corresponding Banach space and taking into account the result on the differentiation of Bochner integral, we find that if
as a complete cone in a corresponding Banach space and taking into account the result on the differentiation of Bochner integral, we find that if 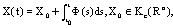 where
where 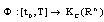 is integrable in the sence of Bochner, then
is integrable in the sence of Bochner, then 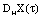 exists and the equality
exists and the equality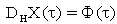 | (2) |
3. Main Results
- Let's consider the set control differential equations (SCDEs):
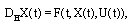 | (3) |
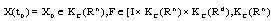
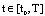 , state
, state 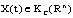 and control
and control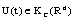 . If
. If 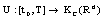 integrable, then it is called an admissible control. Let U be a set of all admissible controls. The mapping
integrable, then it is called an admissible control. Let U be a set of all admissible controls. The mapping 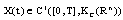 is said to be a solution of SCDES (3) on
is said to be a solution of SCDES (3) on 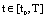 iff it satisfies SCDEs on
iff it satisfies SCDEs on 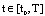 and is the symbolic representation of the following Hukuhara integral expression:
and is the symbolic representation of the following Hukuhara integral expression: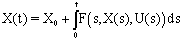 | (4) |
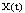 of SCDEs (3) is said to be:a/ (B)- bounded on
of SCDEs (3) is said to be:a/ (B)- bounded on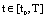 , if there exists the constant
, if there exists the constant 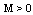 such that, by (4) we have
such that, by (4) we have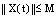 , for all
, for all 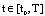 .b/ (EB)- Exponent bounded on
.b/ (EB)- Exponent bounded on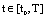 , if there exist the constants
, if there exist the constants 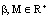 such that the supper distance:
such that the supper distance: 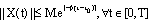 Assume that
Assume that 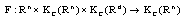 satisfies the followings:(F1). there exists a constant
satisfies the followings:(F1). there exists a constant 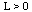 such that
such that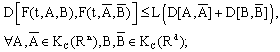 (F2). there exists constant c>0 such that
(F2). there exists constant c>0 such that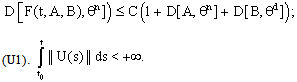 Theorem 3.1. Let
Theorem 3.1. Let 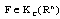 satisfies hypotheses (F1)-(F2) and U satisfies (U1), then SCDEs (3) has unique B- bounded set solutions
satisfies hypotheses (F1)-(F2) and U satisfies (U1), then SCDEs (3) has unique B- bounded set solutions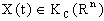 . Proof. We have to prove that: a) By (F1), there exists the set solutions, which is represented as (4). b) Uniqueness of
. Proof. We have to prove that: a) By (F1), there exists the set solutions, which is represented as (4). b) Uniqueness of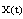 . Assume that the other set solutions
. Assume that the other set solutions 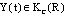 such that
such that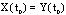 , then
, then 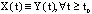 in force (F2). c) A boundedness property of set solution
in force (F2). c) A boundedness property of set solution 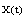 that means there exists
that means there exists 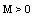 such that
such that 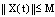 for all
for all 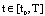 .We estimate
.We estimate 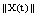 by (4) and (F2):
by (4) and (F2): 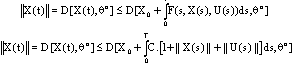 Putting
Putting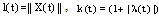 and
and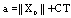 , we have
, we have 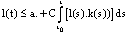 .This Gronwall's inequality implies that
.This Gronwall's inequality implies that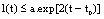 .Choosing
.Choosing 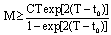 , we have
, we have 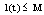 for all
for all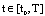 .Theorem 3.2. Let
.Theorem 3.2. Let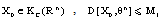 and
and 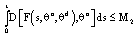 and by contraction feedback
and by contraction feedback 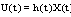 and
and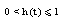 , then SCDEs (3) has the unique (B)- bounded solution in
, then SCDEs (3) has the unique (B)- bounded solution in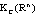 .Proof. (a) Problems of existence and uniqueness are clear.(b) Problem of (B)- bounded are proved by integral expression (4) followings:
.Proof. (a) Problems of existence and uniqueness are clear.(b) Problem of (B)- bounded are proved by integral expression (4) followings: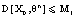 ,and
,and 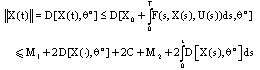 .Using Gronwall's inequality, we infer
.Using Gronwall's inequality, we infer  where
where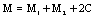 , we obtain
, we obtain 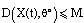 .Next, we present some results about (B), (EB) of solutions in
.Next, we present some results about (B), (EB) of solutions in  with using the Lyapunov-like functions.Theorem 3.3. Assume that the positive Lyapunov - like function
with using the Lyapunov-like functions.Theorem 3.3. Assume that the positive Lyapunov - like function 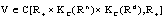 which satisfies the following conditions:(i)
which satisfies the following conditions:(i) 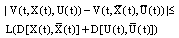 , where L is bounded Lipschitz constant, for all
, where L is bounded Lipschitz constant, for all 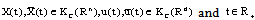 ; (ii)
; (ii)  , for
, for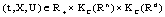 ,where
,where 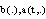 are increasing functions; (iii)
are increasing functions; (iii) 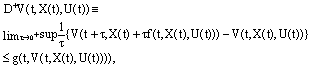 where
where 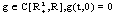 for all
for all 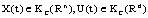 and
and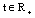 , we have the following affirmations: a/ If
, we have the following affirmations: a/ If 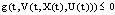 then a set solution
then a set solution 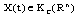 of SCDEs (3) is (B)-bounded. b/ If
of SCDEs (3) is (B)-bounded. b/ If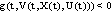 (or if
(or if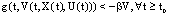 ) then a set solution
) then a set solution 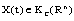 of SCDEs (3) is (EB)-bounded. Proof. Setting the function
of SCDEs (3) is (EB)-bounded. Proof. Setting the function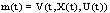 , we have
, we have 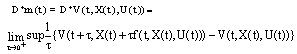
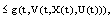 so
so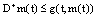 , implies that
, implies that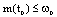 . Since
. Since 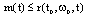 where
where 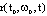 is maximal solution of ODE:
is maximal solution of ODE: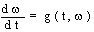 | (5) |
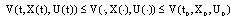 for all
for all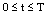 . • Let
. • Let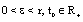 , be given. Choose a
, be given. Choose a 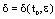 such that
such that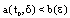 . We claim that with this
. We claim that with this 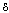 then (B)- bounded solution. If it’s not true, there exists solution
then (B)- bounded solution. If it’s not true, there exists solution 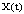 of SCDEs (3) and
of SCDEs (3) and 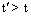 , such that
, such that 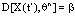 and
and 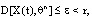 where
where 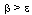 for all
for all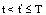 .Wherever
.Wherever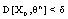 , because
, because 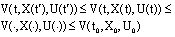 for all
for all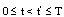 , then :
, then : 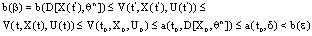 by
by 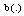 is a increasing function, therefore this contradiction proves that (B)-bounded solution .• In the case, if
is a increasing function, therefore this contradiction proves that (B)-bounded solution .• In the case, if 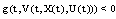 (or
(or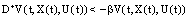 ) then we have
) then we have 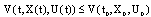 for all
for all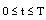 .If
.If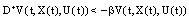 then
then 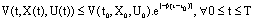 and if (EB) is not true, given
and if (EB) is not true, given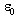 , we choose
, we choose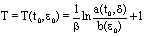 then
then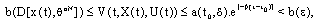 for all
for all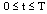 , this contradiction proves that the fuzzy set solution
, this contradiction proves that the fuzzy set solution 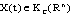 is (EB). Definition 3.2. The set solutions of SCDEs (3) are said to be:a/ (B1)- equi - bounded, if for any
is (EB). Definition 3.2. The set solutions of SCDEs (3) are said to be:a/ (B1)- equi - bounded, if for any 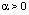 and
and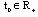 , there exists a
, there exists a 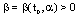 such that
such that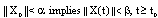 .b/ (B2)- uniform - bounded, if β in (B1) does not depend on
.b/ (B2)- uniform - bounded, if β in (B1) does not depend on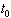 .Theorem 3.4. Assume that the Lyapunov-like function
.Theorem 3.4. Assume that the Lyapunov-like function 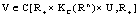 and feedback
and feedback 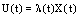 satisfy the following conditions:(i)
satisfy the following conditions:(i) 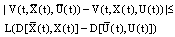 ,where L is bounded Lipschitz constant, for all
,where L is bounded Lipschitz constant, for all 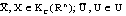 and
and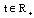 ;(ii) add condition
;(ii) add condition 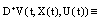
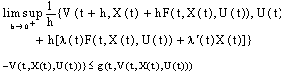 where
where 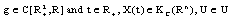 .If
.If 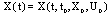 is any solution of SCDEs (3) existing on
is any solution of SCDEs (3) existing on 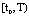 such that
such that 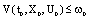 , then we have
, then we have 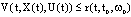 where
where 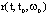 is a maximal solution of ordinary differential equation (ODE) (5)
is a maximal solution of ordinary differential equation (ODE) (5) 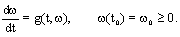 Proof. Let
Proof. Let 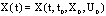 is any solution of SCDEs (3) existing on
is any solution of SCDEs (3) existing on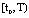 .Define
.Define 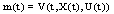 so that
so that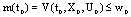 . Now, for small
. Now, for small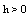 , by our assumption it follows that
, by our assumption it follows that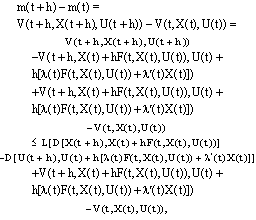 using the Lipschitz condition give (i), thus we have
using the Lipschitz condition give (i), thus we have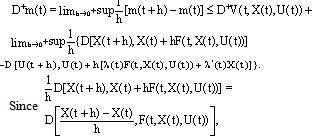 and
and 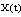 is any solution of SCDEs (3), we find that
is any solution of SCDEs (3), we find that 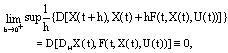 and
and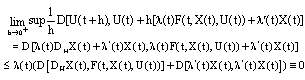 We therefore have the scalar differential inequality
We therefore have the scalar differential inequality 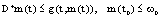 which yields, as before, the estimate
which yields, as before, the estimate 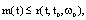 where
where 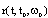 is a maximal solution of ODE (5). This proof is complete.Corollary 3.1. A function
is a maximal solution of ODE (5). This proof is complete.Corollary 3.1. A function 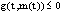 is admissible in the theorem 3.4 to yield the estimate
is admissible in the theorem 3.4 to yield the estimate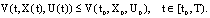 Next, we have some denotes:
Next, we have some denotes: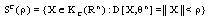 ,
,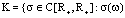 is increasing in
is increasing in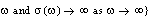 .Now, we introduce some results on the boundedness of set solutions for SCDEs (3) by feedback
.Now, we introduce some results on the boundedness of set solutions for SCDEs (3) by feedback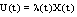 . Theorem 3.5. Assume that
. Theorem 3.5. Assume that 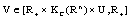 is Lyapunov-like function and
is Lyapunov-like function and 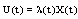 is feedback for SCDEs (3) satisfies the following conditions: (i)
is feedback for SCDEs (3) satisfies the following conditions: (i) 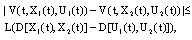 for
for 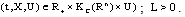 (ii)
(ii) 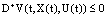 (iii)
(iii) 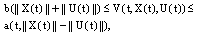 then, the affirmation (B1) holds.Proof. Proof of this theorem is analogous proof of theorem 3.3.Theorem 3.6. Assume that(i)
then, the affirmation (B1) holds.Proof. Proof of this theorem is analogous proof of theorem 3.3.Theorem 3.6. Assume that(i) 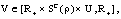 where ρ may be large, satisfies:
where ρ may be large, satisfies: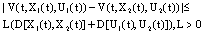 (ii) for
(ii) for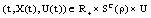 ,
,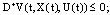 (iii)
(iii) 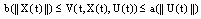 and
and 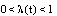 where
where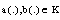 , which are defined only on
, which are defined only on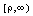 ,then, (B2) holds.Proof. We have to prove that (B2) holds. Because
,then, (B2) holds.Proof. We have to prove that (B2) holds. Because 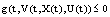 implies
implies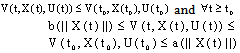 Thus for all
Thus for all 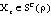 and
and 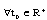 there exists estimate
there exists estimate 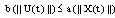 then by (iii) of theorem 3.5 the affirmation for (B1) holds, that means (B2) holds.
then by (iii) of theorem 3.5 the affirmation for (B1) holds, that means (B2) holds.4. Conclusions
- By the Lyapunov like-funcions and by some kinds of feeback we just have investigated the problems of boundedness for set solutions to set control differential equations - SCDES, that is an one of the new trends in set-valued analysis. The boundedness properties of set solutions allows testing the extremal solutions, what is useful in practice of applications SDEs and SCDEs.
ACKNOWLEDGEMENTS
- The authors gratefully acknowledge the referees for their careful reading and many valuable remarks which improved the presentation of the paper.Thanks are due to the Vietnam National Foundation for Science and Technology Devolopment (NAFOSTED) for financial support.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML