Tsouria Zendagui , Mourad Mahboub
Faculty of Sciences, University of Tlemcen, BP.119 Tlemcen, Algeria
Correspondence to: Mourad Mahboub , Faculty of Sciences, University of Tlemcen, BP.119 Tlemcen, Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The generalized nonlinear Schrödinger equation describes the different physical phenomena encountered when ultrashort pulses propagate through dispersive and nonlinear fibers. If the pulse duration is of picoseconds order, the nonlinear Schrödinger equation can be simplified. However the analytical solution remains inaccessible except for some special cases like soliton. The symmetric split-step Fourier method (S-SSFM) which is derived from the Strang formulas, subdivides the global propagation distance into small steps of length h to calculate the numerical solution of this equation. By using only the fact that the dispersive and nonlinear operators do not commute the Baker-Campbell-Hausdorff formula shows that the global relative error of this method is O(h2). Our numerical simulation results show that this error depends also on the self phase modulation nonlinear term. For this purpose, we employ in this work an explicit representation of the nonlinear operator and we present four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 obtained respectively from some weighting coefficients (c0, c1) = (0, 1), (c0, c1) = (1, 0), (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1). Thus, we have computed for an input Gaussian pulse, the numerical solutions and the global relative errors for each implementation. As results, the estimated slopes of the linear variations of the global relative errors allow showing that the S-SSFM1 and T-SM1 errors are O(h), S-SSFM2 and T-SM2 errors are O(h2); furthermore, the S-SSFM is more accurate than the T-SM. In order to obtain an indicator of accuracies, we present the variations of the global relative errors for some values of the propagation length of the fiber.
Keywords:
Schrödinger Equation, Global Relative Error, Symmetric Split-Step Fourier Method
1. Introduction
Ultrashort pulse propagation in dispersive and nonlinear optical fibers is described by the generalized nonlinear Schrödinger equation (G-NLSE)[1,2]: | (1) |
Where 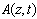 is the amplitude of the variable field, β2 and β3 are respectively, the second and the third order dispersion coefficients, α is the attenuation coefficient and γ is the nonlinear coefficient of the self phase modulation due to optical Kerr effect. is the slope of the Raman gain (stimulated Raman scattering (SRS)) and
is the amplitude of the variable field, β2 and β3 are respectively, the second and the third order dispersion coefficients, α is the attenuation coefficient and γ is the nonlinear coefficient of the self phase modulation due to optical Kerr effect. is the slope of the Raman gain (stimulated Raman scattering (SRS)) and 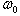 is the center angular frequency. The term proportional to
is the center angular frequency. The term proportional to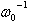 in the second member represents the self-steepening effect.The generalized nonlinear Schrödinger equation is knownto be applicable for femtosecond pulses; it can be simplified when the pulse width is of picosecond order (not less than 5ps). The Raman effect and the self-steepening effect terms can be neglected compared to the self phase modulation term[3]. For such pulses the contribution of the third order dispersion is also quite small compared to the second order dispersion term unless operation is near the zero of the group velocity dispersion (where β2 is null). The simplified NLSE is then given by the following equation:
in the second member represents the self-steepening effect.The generalized nonlinear Schrödinger equation is knownto be applicable for femtosecond pulses; it can be simplified when the pulse width is of picosecond order (not less than 5ps). The Raman effect and the self-steepening effect terms can be neglected compared to the self phase modulation term[3]. For such pulses the contribution of the third order dispersion is also quite small compared to the second order dispersion term unless operation is near the zero of the group velocity dispersion (where β2 is null). The simplified NLSE is then given by the following equation: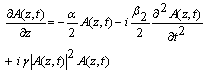 | (2) |
This equation can be written as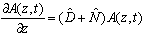 | (3) |
with a linear operator 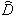 and a nonlinear operator
and a nonlinear operator 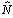 defined as
defined as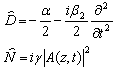 | (4) |
Equation (2) cannot be solved analytically except for some special cases like soliton where the dispersion effects are compensated by the optical Kerr effect[4-6].Several methods has been developed to determine the numerical solution of this equation, the most important are called operator splitting methods and the widely used are the Lie formulas[7] : 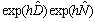
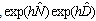 and the Strang formulas[8] :
and the Strang formulas[8] : 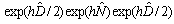 ,
,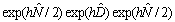 .The nonlinear term is solved in time domain, whereas the dispersion term is solved in the frequency domain and requires some fast Fourier transform (FFT) routines. From the Lie formulas derive the split-step Fourier method (SSFM), and the Strang formulas lead to the symmetric split step Fourier method (S-SSFM).In the split-step Fourier method (SSFM), the global propagation distance is subdivides into steps of length h, sufficiently small, and the approximate solution is obtained by supposing that along each step the effects of dispersion and nonlinearity are assumed to be independent. The error of this method derives from the fact that the operators of dispersion and nonlinearity do not commute. To improve the precision, we must consider another procedure for the pulse propagation where the effects of nonlinearity (or dispersion) are inserted at the middle of each step of the fiber. This is known as the symmetric split step Fourier method (S-SSFM) and its description are given in paragraph 2. In the paragraph 3, we study the effect of the nonlinear term
.The nonlinear term is solved in time domain, whereas the dispersion term is solved in the frequency domain and requires some fast Fourier transform (FFT) routines. From the Lie formulas derive the split-step Fourier method (SSFM), and the Strang formulas lead to the symmetric split step Fourier method (S-SSFM).In the split-step Fourier method (SSFM), the global propagation distance is subdivides into steps of length h, sufficiently small, and the approximate solution is obtained by supposing that along each step the effects of dispersion and nonlinearity are assumed to be independent. The error of this method derives from the fact that the operators of dispersion and nonlinearity do not commute. To improve the precision, we must consider another procedure for the pulse propagation where the effects of nonlinearity (or dispersion) are inserted at the middle of each step of the fiber. This is known as the symmetric split step Fourier method (S-SSFM) and its description are given in paragraph 2. In the paragraph 3, we study the effect of the nonlinear term 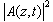 on the S-SSFM global relative error. We present for this purpose four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 and we will show numerically that this error depends on the nonlinear term and is O(h) or O(h2). However, the S-SSFM algorithms are more accurate than the T-SM. We present the numerical results in paragraph 4 and a conclusion of this work is given in paragraph 5.
on the S-SSFM global relative error. We present for this purpose four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 and we will show numerically that this error depends on the nonlinear term and is O(h) or O(h2). However, the S-SSFM algorithms are more accurate than the T-SM. We present the numerical results in paragraph 4 and a conclusion of this work is given in paragraph 5.
2. The Symmetric Split-Step Fourier Method
If the step h is sufficiently small, we can neglect the variations of the nonlinear operator 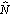 in the interval[z, z+h] and the formal solution of the variable field amplitude A(z+h, t) in terms of A(z, t) is given by the following equation:
in the interval[z, z+h] and the formal solution of the variable field amplitude A(z+h, t) in terms of A(z, t) is given by the following equation: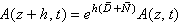 | (5) |
The two operators 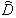 and
and 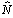 do not commute thus the calculation of A(z, t) is difficult to realize. Equation (5) can be approached by the following equation:
do not commute thus the calculation of A(z, t) is difficult to realize. Equation (5) can be approached by the following equation: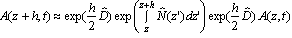 | (6) |
or by the equation: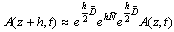 | (7) |
An argument based on the Baker-Campbell-Hausdorff formula[9] shows that the local error, which is the error along one step of length h of the symmetric split-step scheme is O(h3). Since the total number of the steps in a fiber is inversely proportional to the spatial step length h, the global relative error accumulated along the whole fiber is O(h2)[10,11].
3. Evaluation of the Nonlinear Operator
The nonlinear operator can be approximated by using the trapezoidal rule: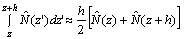 | (8) |
However 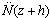 cannot be known at z+h/2, then we propose two implementations. We exploit an explicit representation of the nonlinear operator
cannot be known at z+h/2, then we propose two implementations. We exploit an explicit representation of the nonlinear operator 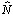 where the attenuation factor α is neglected and by using equations (2) and (7), we compute numerically the output pulse along a step from an input pulse A(0,t) at the entry of the fiber as following:
where the attenuation factor α is neglected and by using equations (2) and (7), we compute numerically the output pulse along a step from an input pulse A(0,t) at the entry of the fiber as following: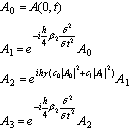 | (9) |
Step by step, we compute recursively the output pulse at the end of the fiber. The choice of the coefficients c0 and c1 is crucial for the computation errors of the method. In order to evaluate the performance of these implementations, we use the global relative error δ given by the following equation[12]: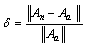 | (10) |
Where Aa is the fine numerical solution at the end of the fiber computed for a very small and constant value of the step size h; the norm  is defined by:
is defined by: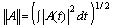 | (11) |
In this work, we present a numerical estimation of the global relative error (GRE) of the S-SSFM for two implementations: (c0, c1) = (0, 1) and (c0, c1) = (1, 0) which we design respectively by S-SSFM1 and S-SSFM2. We show that the GRE is respectively O(h) and O(h2).Then, we consider the second formula of the Strang splitting and we make a permutation in the position of the two operators 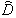 and
and 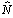 in equation (7), the solution will be numerically computed from the input pulse A(0,t) as following:
in equation (7), the solution will be numerically computed from the input pulse A(0,t) as following: 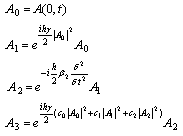 | (12) |
We can see that the nonlinear operator will be applied in two steps. First, we must introduce the intensity 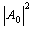 to calculate the nonlinear term of A1. Second, there exist several combinations of the intensities
to calculate the nonlinear term of A1. Second, there exist several combinations of the intensities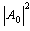 ,
, 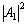 and
and 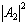 pondered respectively by three coefficients c0, c1 and c2 to compute the nonlinear term of A3. This approach is also called the three-split method and designed by T-SM[13]. From
pondered respectively by three coefficients c0, c1 and c2 to compute the nonlinear term of A3. This approach is also called the three-split method and designed by T-SM[13]. From 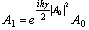 it is clear that
it is clear that 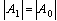 (nonlinear operator introduces only phase shift), and consequently, for some combinations like (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1) relation
(nonlinear operator introduces only phase shift), and consequently, for some combinations like (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1) relation 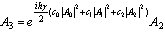 simplifies to
simplifies to 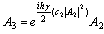 . Therefore, in this work, we show that the GRE of the T-SM is O(h) for the combination (c0,c1,c2) = (1,1,-1) which we design by T-SM1 and the GRE is O(h2) for the combination (c0,c1,c2) = (-1,1,1) which we design by T-SM2.
. Therefore, in this work, we show that the GRE of the T-SM is O(h) for the combination (c0,c1,c2) = (1,1,-1) which we design by T-SM1 and the GRE is O(h2) for the combination (c0,c1,c2) = (-1,1,1) which we design by T-SM2.
4. Numerical Results
We consider in our simulation a silica single mode fiber and we study in the dispersive and nonlinear regime, the propagation of a Gaussian pulse for which the amplitude of the incident field can be written as: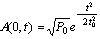 | (13) |
The corresponding parameters are as following: β2 = -20 ps2/km in an optical telecommunication window around λ0 = 1,55 μm, γ = 2 W -1km-1, P0 = 5 mW and t0 = 40 ps. We compute the numerical output solutions An, using the four implementations, by considering the transmission distance z = 200 km, with a spatial step size h = 1 km. The correspondent curves are plotted in Figure 1a.We note a temporal broadening of the output pulses, due to dispersion and a diminution of the maximal intensity. It seems that the numerical results are identical, but if we zoom the framed part in Figure 1a, we obtain the Figure 1b in which we can see the differences between the numerical values.| Table 1. Global relative errors calculated using the four implementations for z = 200km |
| | h(km) | 0.03125 | 0.0625 | 0.125 | 0.25 | 0.5 | 1 | Estimated order α | | GRE S-SSFM1 | 1.5 10-5 | 3.5 10-5 | 7.5 10-5 | 1.6 10-4 | 3.2 10-4 | 6.4 10-4 | 1.078 | | GRE S-SSFM2 | 5.6 10-9 | 2.3 10-8 | 9.5 10-8 | 3.8 10-7 | 1.5 10-6 | 6.1 10-6 | 2.018 | | GRE T-SM1 | 6.0 10-5 | 1.4 10-4 | 3.0 10-4 | 6.2 10-4 | 1.2 10-3 | 2.5 10-3 | 1.155 | | GRE T-SM2 | 1.6 10-8 | 7.0 10-8 | 2.8 10-7 | 1.1 10-6 | 4.5 10-6 | 1.8 10-5 | 2.063 |
|
|
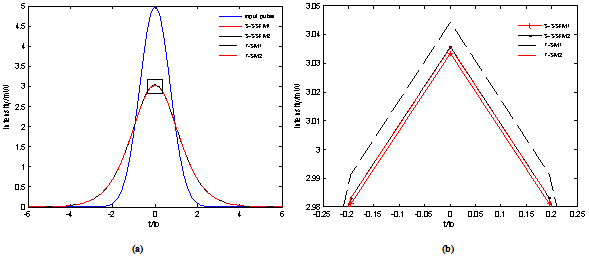 | Figure 1. (a) The input pulse and some output pulses for z = 200 km, (b) zoom of the part inside the square of the output pulses |
We have measured the variation of the global relative error for the four implementations: S-SSFM1, S-SSFM2, T-SM1 and T-SM2 against the spatial step size h. We note that the fine numerical solution Aa is computed for h = 7.8 m. The corresponding curves are plotted in Figure 2. We prove by using a graphic log-log that the global relative error can be estimated by formulas of type δ = Chα. More precisely we have verified by a linear regression in the graphic, that the order of h is practically equal to 1 for the S-SSFM1 and T-SM1 and 2 for the S-SSFM2 and T-SM2. The detailed results are presented in table 1. We can also show from the curves of Figure 2 that the S-SSFM implementations are more accurate than the T-SM.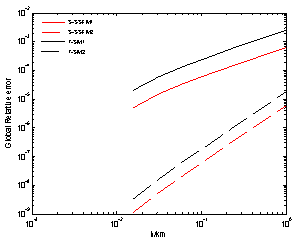 | Figure 2. Global relative error for z = 200km vs. step size h |
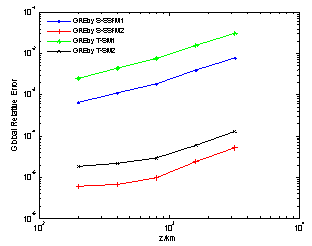 | Figure 3. Global relative error for h =1km vs. propagation distance z |
The estimated GRE for the S-SSFM2 and T-SM2 is O(h2) which corresponds substantially to the commutator error. The nonlinear term has practically no influence on these implementations rather than the S-SSFM1 and the T-SM1 for which the GRE is O(h), decreased by one order and depends on the nonlinear term.In the Figure 3, we plot the GRE variation curves for the four implementations for h = 1 km versus the propagation length z. These curves will be an indicator of accuracy and allow deciding the step size to be taken in a wide range of situations of practical interest.
5. Conclusions
The propagation of picoseconds pulses in optical fibers is described by the simplified Schrödinger equation. The symmetric split-step Fourier method is often used to calculate the numerical solution of this equation. If we consider the only fact that the dispersive and nonlinear operators do not commute the Baker-Campbell-Hausdorff formula shows that the global relative error of this method is O(h2). We have analysed in this paper, the effect of the nonlinear self phase modulation, which depends on the intensity term 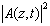 , on the global relative error. By using the two Strang splitting formulas and an explicit representation of the nonlinear operator, we have presented four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 obtained from different forms of the approximate nonlinear term and respectively for the weighting coefficients (c0, c1) = (0, 1), (c0, c1) = (1, 0), (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1). Our numerical results prove that this error is O(h) or O(h2). We conclude that the nonlinear term has an influence on the splitting error, the S-SSFM is more accurate than the T-SM and in order to obtain an indicator of accuracies, we present the variations of the global relative errors for some values of the propagation length of the fiber.
, on the global relative error. By using the two Strang splitting formulas and an explicit representation of the nonlinear operator, we have presented four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 obtained from different forms of the approximate nonlinear term and respectively for the weighting coefficients (c0, c1) = (0, 1), (c0, c1) = (1, 0), (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1). Our numerical results prove that this error is O(h) or O(h2). We conclude that the nonlinear term has an influence on the splitting error, the S-SSFM is more accurate than the T-SM and in order to obtain an indicator of accuracies, we present the variations of the global relative errors for some values of the propagation length of the fiber.
References
| [1] | Govind P. Agrawal: Nonlinear Fiber Optics, 4th ed., Academic Press, Boston, 2007. |
| [2] | Mourad Mahboub, Tsouria Zendagui, "Global relative error evaluation of the split-step Fourier method (S-SSFM ): Ultrafast pulses propagation in nonlinear and dispersive optical fibers", Proceedings of V Seminar SENALAP2009, December 16-17, 2009. |
| [3] | M. Tiwari, V. Janyani, "Two-Octave Spanning Supercontinuum in a Soft Glass Photonic Crystal Fiber Suitable for 1.55 m Pumping", Journal of Lightwave Technology 29(23), 2011, pp. 3560-3565. |
| [4] | H. Ghafouri-Shiraz, M. Nagata, P. Shum, "A novel method for analysis of soliton propagation in optical fibers", IEEE Journal Quantum Electron 31(1), 1995, pp. 190-200. |
| [5] | T. R. Taha, M. J. Ablowitz, "Analytical and numerical aspects of certain nonlinear evolution equations. II. Numerical, nonlinear Schrödinger equation", Journal Computing Physics 55(2), 1984, pp.203-230. |
| [6] | A. Fazacas, P. Sterian, " Second and third order dispersion effects analyzed by the split-step Fourier method for soliton propagation in optical fibers", Journal of Optoelectronics and Advanced Materials 14(3-4), 2012, pp. 376-382. |
| [7] | S. Yu, S. Zhao, G.W. Wei, "Local spectral time splitting method for first- and second-order partial differential equations", journal of Computational Physics 206(2), 2005, pp. 727-780. |
| [8] | G. Strang, "On the construction and comparison of difference schemes", SIAM Journal on Numerical Analysis 5(3), 1968, pp. 506–517. |
| [9] | Q. Zhang and M. I. Hayee, "Symmetrized split-step Fourier scheme to control global simulation accuracy in fiber-optic communication systems", Journal of Lightwave Technology, 26(2), (2008), pp. 302-316. |
| [10] | V.C. Long, H.N. Viet, M Trippenbach, K.D. Xuan, "Propagation Technique for Ultrashort Pulses III: Pulse Splitting of Ultrashort Pulses in a Kerr Medium", Computational Methods in Science and Technology 14(1), 2008, pp. 21-26. |
| [11] | T. Hohage, F. Schmidt, "On the numerical solution of nonlinear Schrödinger type equation in fiber optics", Technical Report 02-01, Zuse Institute Berlin, 2002. |
| [12] | O.V. Sinkin, R. Holzlöhner, J. Zweck, C.R. Menyuk, "Optimization of the split-step Fourier method in modeling optical fiber communications systems", Journal of Lightwave Technology 21(1), 2003, pp. 61-68. |
| [13] | J. Javanainen, J. Ruostekoski, "Symbolic calculation in development of algorithms: split-step methods for the Gross–Pitaevskii equation", Journal of Physics A: Mathematical and General 39(12), 2006, L179-L18. |

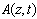 is the amplitude of the variable field, β2 and β3 are respectively, the second and the third order dispersion coefficients, α is the attenuation coefficient and γ is the nonlinear coefficient of the self phase modulation due to optical Kerr effect. is the slope of the Raman gain (stimulated Raman scattering (SRS)) and
is the amplitude of the variable field, β2 and β3 are respectively, the second and the third order dispersion coefficients, α is the attenuation coefficient and γ is the nonlinear coefficient of the self phase modulation due to optical Kerr effect. is the slope of the Raman gain (stimulated Raman scattering (SRS)) and 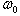 is the center angular frequency. The term proportional to
is the center angular frequency. The term proportional to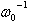 in the second member represents the self-steepening effect.The generalized nonlinear Schrödinger equation is knownto be applicable for femtosecond pulses; it can be simplified when the pulse width is of picosecond order (not less than 5ps). The Raman effect and the self-steepening effect terms can be neglected compared to the self phase modulation term[3]. For such pulses the contribution of the third order dispersion is also quite small compared to the second order dispersion term unless operation is near the zero of the group velocity dispersion (where β2 is null). The simplified NLSE is then given by the following equation:
in the second member represents the self-steepening effect.The generalized nonlinear Schrödinger equation is knownto be applicable for femtosecond pulses; it can be simplified when the pulse width is of picosecond order (not less than 5ps). The Raman effect and the self-steepening effect terms can be neglected compared to the self phase modulation term[3]. For such pulses the contribution of the third order dispersion is also quite small compared to the second order dispersion term unless operation is near the zero of the group velocity dispersion (where β2 is null). The simplified NLSE is then given by the following equation: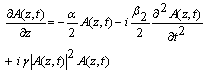
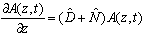
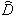 and a nonlinear operator
and a nonlinear operator 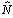 defined as
defined as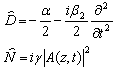
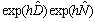
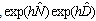 and the Strang formulas[8] :
and the Strang formulas[8] : 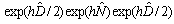 ,
,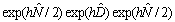 .The nonlinear term is solved in time domain, whereas the dispersion term is solved in the frequency domain and requires some fast Fourier transform (FFT) routines. From the Lie formulas derive the split-step Fourier method (SSFM), and the Strang formulas lead to the symmetric split step Fourier method (S-SSFM).In the split-step Fourier method (SSFM), the global propagation distance is subdivides into steps of length h, sufficiently small, and the approximate solution is obtained by supposing that along each step the effects of dispersion and nonlinearity are assumed to be independent. The error of this method derives from the fact that the operators of dispersion and nonlinearity do not commute. To improve the precision, we must consider another procedure for the pulse propagation where the effects of nonlinearity (or dispersion) are inserted at the middle of each step of the fiber. This is known as the symmetric split step Fourier method (S-SSFM) and its description are given in paragraph 2. In the paragraph 3, we study the effect of the nonlinear term
.The nonlinear term is solved in time domain, whereas the dispersion term is solved in the frequency domain and requires some fast Fourier transform (FFT) routines. From the Lie formulas derive the split-step Fourier method (SSFM), and the Strang formulas lead to the symmetric split step Fourier method (S-SSFM).In the split-step Fourier method (SSFM), the global propagation distance is subdivides into steps of length h, sufficiently small, and the approximate solution is obtained by supposing that along each step the effects of dispersion and nonlinearity are assumed to be independent. The error of this method derives from the fact that the operators of dispersion and nonlinearity do not commute. To improve the precision, we must consider another procedure for the pulse propagation where the effects of nonlinearity (or dispersion) are inserted at the middle of each step of the fiber. This is known as the symmetric split step Fourier method (S-SSFM) and its description are given in paragraph 2. In the paragraph 3, we study the effect of the nonlinear term 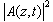 on the S-SSFM global relative error. We present for this purpose four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 and we will show numerically that this error depends on the nonlinear term and is O(h) or O(h2). However, the S-SSFM algorithms are more accurate than the T-SM. We present the numerical results in paragraph 4 and a conclusion of this work is given in paragraph 5.
on the S-SSFM global relative error. We present for this purpose four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 and we will show numerically that this error depends on the nonlinear term and is O(h) or O(h2). However, the S-SSFM algorithms are more accurate than the T-SM. We present the numerical results in paragraph 4 and a conclusion of this work is given in paragraph 5.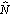 in the interval[z, z+h] and the formal solution of the variable field amplitude A(z+h, t) in terms of A(z, t) is given by the following equation:
in the interval[z, z+h] and the formal solution of the variable field amplitude A(z+h, t) in terms of A(z, t) is given by the following equation: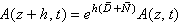
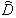 and
and 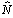 do not commute thus the calculation of A(z, t) is difficult to realize. Equation (5) can be approached by the following equation:
do not commute thus the calculation of A(z, t) is difficult to realize. Equation (5) can be approached by the following equation: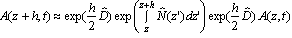
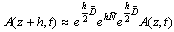
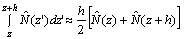
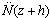 cannot be known at z+h/2, then we propose two implementations. We exploit an explicit representation of the nonlinear operator
cannot be known at z+h/2, then we propose two implementations. We exploit an explicit representation of the nonlinear operator  where the attenuation factor α is neglected and by using equations (2) and (7), we compute numerically the output pulse along a step from an input pulse A(0,t) at the entry of the fiber as following:
where the attenuation factor α is neglected and by using equations (2) and (7), we compute numerically the output pulse along a step from an input pulse A(0,t) at the entry of the fiber as following:
 is defined by:
is defined by:
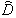 and
and 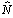 in equation (7), the solution will be numerically computed from the input pulse A(0,t) as following:
in equation (7), the solution will be numerically computed from the input pulse A(0,t) as following: 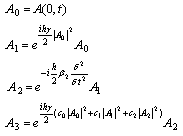
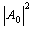 to calculate the nonlinear term of A1. Second, there exist several combinations of the intensities
to calculate the nonlinear term of A1. Second, there exist several combinations of the intensities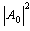 ,
, 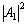 and
and 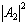 pondered respectively by three coefficients c0, c1 and c2 to compute the nonlinear term of A3. This approach is also called the three-split method and designed by T-SM[13]. From
pondered respectively by three coefficients c0, c1 and c2 to compute the nonlinear term of A3. This approach is also called the three-split method and designed by T-SM[13]. From 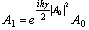 it is clear that
it is clear that 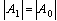 (nonlinear operator introduces only phase shift), and consequently, for some combinations like (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1) relation
(nonlinear operator introduces only phase shift), and consequently, for some combinations like (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1) relation 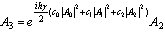 simplifies to
simplifies to 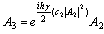 . Therefore, in this work, we show that the GRE of the T-SM is O(h) for the combination (c0,c1,c2) = (1,1,-1) which we design by T-SM1 and the GRE is O(h2) for the combination (c0,c1,c2) = (-1,1,1) which we design by T-SM2.
. Therefore, in this work, we show that the GRE of the T-SM is O(h) for the combination (c0,c1,c2) = (1,1,-1) which we design by T-SM1 and the GRE is O(h2) for the combination (c0,c1,c2) = (-1,1,1) which we design by T-SM2.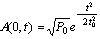



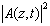 , on the global relative error. By using the two Strang splitting formulas and an explicit representation of the nonlinear operator, we have presented four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 obtained from different forms of the approximate nonlinear term and respectively for the weighting coefficients (c0, c1) = (0, 1), (c0, c1) = (1, 0), (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1). Our numerical results prove that this error is O(h) or O(h2). We conclude that the nonlinear term has an influence on the splitting error, the S-SSFM is more accurate than the T-SM and in order to obtain an indicator of accuracies, we present the variations of the global relative errors for some values of the propagation length of the fiber.
, on the global relative error. By using the two Strang splitting formulas and an explicit representation of the nonlinear operator, we have presented four implementations: the S-SSFM1, S-SSFM2, T-SM1 and T-SM2 obtained from different forms of the approximate nonlinear term and respectively for the weighting coefficients (c0, c1) = (0, 1), (c0, c1) = (1, 0), (c0,c1,c2) = (-1,1,1) and (c0,c1,c2) = (1,-1,1). Our numerical results prove that this error is O(h) or O(h2). We conclude that the nonlinear term has an influence on the splitting error, the S-SSFM is more accurate than the T-SM and in order to obtain an indicator of accuracies, we present the variations of the global relative errors for some values of the propagation length of the fiber. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML