O. P. Misra 1, Dinesh Kumar Mishra 2
1School of Mathematics and allied sciences, Jiwaji University, Gwalior 474011 Madhya Pradesh, India
2Department of Mathematics S.L.P. Govt. P.G. College, Gwalior 474006 Madhya Pradesh, India
Correspondence to: Dinesh Kumar Mishra , Department of Mathematics S.L.P. Govt. P.G. College, Gwalior 474006 Madhya Pradesh, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Chikungunya is a vector borne communicable disease which is transmitted in human population through the bite of an infected Aedes-Aegeypti mosquito. In order to study the spread of Chikungunya disease a model has been proposed and analyzed in this paper. In the proposed model the human population and the mosquito population have been divided into three and two classes respectively. For controlling the disease, vector control measures such as, reduction in the breeding of vector population, killing of mosquitoes and isolation of infected humans have been also taken in to account in the model. Linear and non-linear stability analysis of the model has been carried out. From the analysis we have derived a threshold condition involving control reproductive number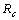 , and we have found that the disease free equilibrium point is locally asymptotically stable when
, and we have found that the disease free equilibrium point is locally asymptotically stable when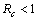 and unstable when
and unstable when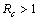 .We have also proved that a unique endemic equilibrium point exists and is locally asymptotically stable when
.We have also proved that a unique endemic equilibrium point exists and is locally asymptotically stable when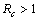 . Thus, we have concluded from the analysis of the model that the disease will either die out or will remain endemic depending on the value of control reproductive number. This study will assist the health department in controlling the spread of Chikungunya disease by introducing the control measures such as increasing the awareness in the society, killing of mosquitoes and isolating the infected individuals.
. Thus, we have concluded from the analysis of the model that the disease will either die out or will remain endemic depending on the value of control reproductive number. This study will assist the health department in controlling the spread of Chikungunya disease by introducing the control measures such as increasing the awareness in the society, killing of mosquitoes and isolating the infected individuals.
Keywords:
Chikungunya Disease, Epidemic Model, Control Reproductive Number, Stability, Disease Free Equilibrium Point, Endemic Equilibrium Point
1. Introduction
Chikungunya is a vector borne communicable disease. It is caused by a Buggy creek virus or better known as Chikungunya virus. This virus is an enveloped positive-strand RNA virus capable of replicating in a mosquito species known as ades-aegeypti. Aedes-aegeypti mosquitoes usually dwell in human habitats. Chikungunya virus is transmitted in the human individuals through the bite of an Aedes-Aegeypti mosquito. Chikungunya disease has become a global concern due to an escalation in the disease outbreaks, in Africa, India and South East Asian countries. The epidemic is a consequence of heavy rains favoring the active breeding of these mosquitoes in urban habitats that synchronize with humans, who serve as reservoir host for Chikungunya virus.Aedes-aegeypti is a household container breeder and aggressive anthrophilic day time biter. Apart from other containers like clay jars, drums, cement tanks and coolers, west bottles are also found to be positive for aedes breeding. According to a survey report[15] more than 80% breeding has been found in small and midsized containers.Since no vaccine or specific antiviral treatment available for Chikungunya fever, vector avoidance and control is atpresent the only way to limit the disease transmission. As we know that most of the Chikungunya vector population grows in household containers therefore education of society can play an effective role to curb the vector breeding. Simultaneously chemical spray can eliminate the vector presented in the surroundings of human habitat. A new ULV technique consisting of aerosol spray of ultra low volume quantities of insecticide has been found to be effective in killing the mosquito in the air as well as on the water. With the help of ULV treatment the Aedes Research unit Bangkok was able to reduce adult mosquito density by more then 98% for several weeks[12]. Further, spread of the infection can be reduced by isolating infected humans from mosquitoes. This can be done by staying indoors and sleeping under mosquito nets.Dynamics of various vector borne diseases has been studied by various researchers such as N.T.J.Bailey[3], Aron[2], Anderson and May[1], Esteva and Vardos[9,10], Diekmann and Heesterbeek[7], Chitnis et. al[5,6] and Bacaër[4] using mathematical models.Ramchurn et. al[13] have specifically studied the transmission dynamics of chikungunya epidemic outbreak with the help of a SI model. In the present work we have developed and extended the model in light of the dynamics of the chikungunya disease.Thus in this paper we have studied an epidemic model for chikungunya disease by considering SIR dynamics for human population and SI dynamics for mosquito population. Through this model we have discussed effects of control measures on the transmission dynamics of chikungunya disease.
2. Model Formulation
In the formulation of the proposed model the human population have been classified into three categories, namely susceptible, infected and removed. Similarly mosquito population has been classified into two categories namely susceptible and infected mosquitoes. When an infected mosquito bites a susceptible human then he gets infection and goes to the infected human class. As chikungunya is not a killer disease[14] and after recovery infected human acquires immunity for significant time therefore after recovery infected humans go to removed class. It has been also assumed in the model that the infected human individuals are kept away from the contact of the mosquitoes by different means such as use of mosquito net, staying at isolated place in the house. Similarly when a susceptible mosquito bites an infected human then it gets infected and joins the infected mosquito class. The transfer diagram of this process is shown in following figure 1.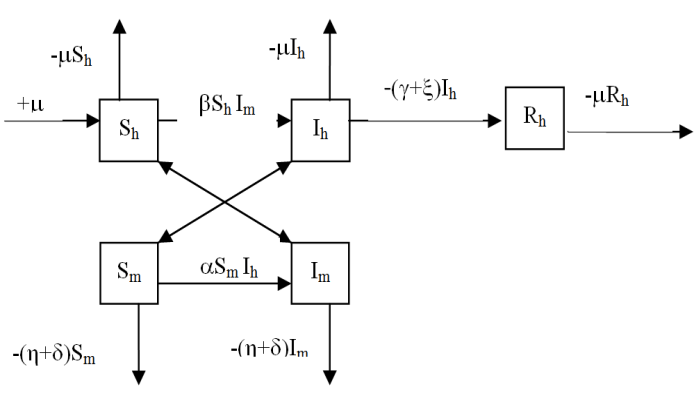 | Figure 1. Transfer diagram of Chikungunya |
Let 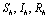 are the proportions of the susceptible, infectious and removed individuals in the human population and
are the proportions of the susceptible, infectious and removed individuals in the human population and 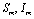 are the proportions of the susceptible and infected mosquitoes in the mosquito population. The dynamical system representing the epidemic spread in human and vector population are then given by the following system of non linear ordinary differential equations.
are the proportions of the susceptible and infected mosquitoes in the mosquito population. The dynamical system representing the epidemic spread in human and vector population are then given by the following system of non linear ordinary differential equations.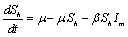 | (2.1a) |
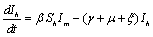 | (2.1b) |
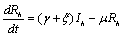 | (2.1c) |
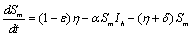 | (2.1d) |
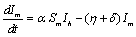 | (2.1e) |
With initial conditions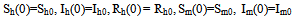 | (2.2) |
The description of parameters is as followsμ = birth and death rates of humans.η = birth and death rates of mosquitoes.β= rate of transmission from infected mosquito to susceptible human.α= rate of transmission from infected human to susceptible mosquito.γ = recovery rate of humans.ξ= rate at which infected humans are isolated from mosquitoes.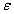 = Rate of awareness programme for reducing vector breeding. (
= Rate of awareness programme for reducing vector breeding. ( ).δ = Killing rate of mosquitoes by spraying chemicals. Let
).δ = Killing rate of mosquitoes by spraying chemicals. Let 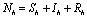 and
and 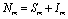 are total population sizes of human and mosquitoes respectively. Then
are total population sizes of human and mosquitoes respectively. Then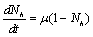 | (2.3a) |
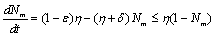 | (2.3b) |
This implies that 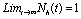 and
and 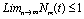 It can be easily seen that the feasible region
It can be easily seen that the feasible region 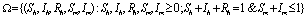 is positively invariant for the model(2.1).Thus, we restrict our attention to the dynamics of the model in
is positively invariant for the model(2.1).Thus, we restrict our attention to the dynamics of the model in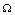 .Using
.Using 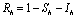 in
in 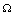 equation(2.1c) can be removed from the model. Therefore we have to study only following four equations.
equation(2.1c) can be removed from the model. Therefore we have to study only following four equations.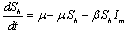 | (2.4a) |
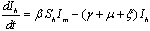 | (2.4b) |
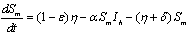 | (2.4c) |
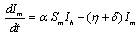 | (2.4d) |
3. Disease Free Equilibrium Point and Reproductive Number
The model (2.4) has exactly one equilibrium point E1(1, 0, 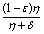 , 0) in the region
, 0) in the region 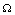 , with no disease in the population.We use the next generation matrix approach as described by Diekmann et. al[8] and Hefferman et. al[11] to define the reproductive number
, with no disease in the population.We use the next generation matrix approach as described by Diekmann et. al[8] and Hefferman et. al[11] to define the reproductive number 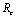 which we call control reproductive number, as the number of secondary infections that one infectious individual would create over the duration of the infectious period in the presence of control measures, provided that everyone else is susceptible. For the model (2.4)
which we call control reproductive number, as the number of secondary infections that one infectious individual would create over the duration of the infectious period in the presence of control measures, provided that everyone else is susceptible. For the model (2.4)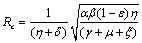 | (3.1) |
When there is no control measure applied, then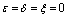 . In this condition the control reproductive number become basic reproductive number
. In this condition the control reproductive number become basic reproductive number  and
and 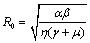 | (3.2) |
it is clear that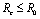 .
.
4. Stability of the Disease Free Equilibrium Point
Applying the transformations,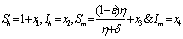 in (2.4) we have,
in (2.4) we have,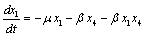 | (4.1a) |
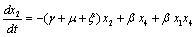 | (4.1b) |
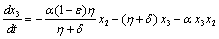 | (4.1c) |
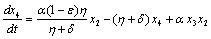 | (4.1d) |
4.1. Local Stability Analysis of Disease Free Equilibrium Point
The linearized system of (2.4) around E0 is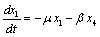 | (4.2a) |
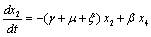 | (4.2b) |
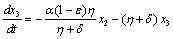 | (4.2c) |
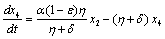 | (4.2d) |
The Jacobian of linearized system around E0 is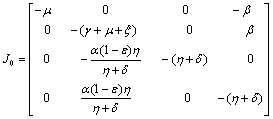 Two characteristic roots of
Two characteristic roots of 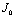 are -
are -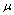 and -
and -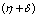 which are negative and remaining two characteristic roots are obtained by solving quadratic equation.
which are negative and remaining two characteristic roots are obtained by solving quadratic equation.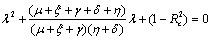 | (4.3) |
Roots of the equation (4.3) are either negative or have negative real parts only when 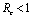 and has exactly one positive root if
and has exactly one positive root if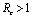 .Thus we have established the following result.Theorem 4.1. The disease free equilibrium point E0 is locally asymptotically stable if
.Thus we have established the following result.Theorem 4.1. The disease free equilibrium point E0 is locally asymptotically stable if 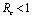 and unstable if
and unstable if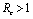 .
.
4.2. Non Linear Stability Analysis of Disease Free Equilibrium Point
Consider a positive definite function 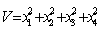 | (4.4) |
then using the non-linear system (4.1) in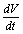 , we get
, we get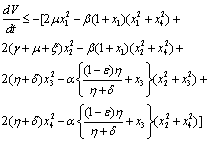 Now using the inequality
Now using the inequality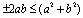 on the right hand side of
on the right hand side of 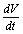 we find that
we find that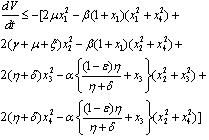 | (4.5) |
Again using the region 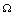 on the right hand side of the above inequality (4.1) we get
on the right hand side of the above inequality (4.1) we get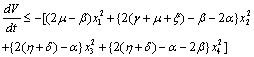 Now, it can be easily seen that
Now, it can be easily seen that 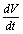 is negative definite under the following conditions.
is negative definite under the following conditions.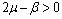 | (4.6a) |
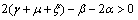 | (4.6b) |
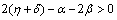 | (4.6c) |
Therefore by Lyapunov’s second method of stability we state the following result.Theorem 4.2. The disease free equilibrium point E0 is non-linearly asymptotically stable if the following three conditions are being satisfied.(i) 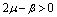 (ii)
(ii) 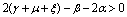 (iii)
(iii) 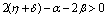 To predict the behaviour of
To predict the behaviour of 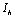 we have solved the linearized system (4.2) around E0.From equations (4.2b) and (4.2d) we get
we have solved the linearized system (4.2) around E0.From equations (4.2b) and (4.2d) we get 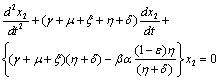 | (4.7) |
Above equation is a second order ordinary differential equation with constant coefficient.The auxiliary equation of (4.7) is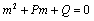 | (4.8) |
Where 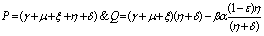 If two roots of (4.7) are
If two roots of (4.7) are 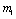 and
and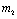 then,
then, 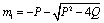 and
and 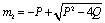 Since
Since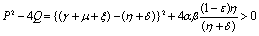 Therefore both the roots of (4.8) are real. Root
Therefore both the roots of (4.8) are real. Root 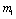 is always negative and
is always negative and 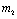 is negative if
is negative if 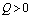 and positive if
and positive if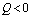 .Again
.Again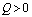
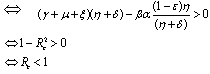 Thus
Thus 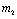 is negative if
is negative if 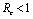 and is positive if
and is positive if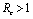 .Now solution of (4.7) is
.Now solution of (4.7) is 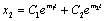 (4.9)Where,
(4.9)Where, 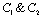 are constants of integration. Now if
are constants of integration. Now if 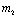 is negative then
is negative then 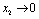 as
as 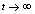 and if
and if 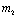 is positive then
is positive then 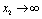 as
as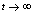 , i.e. as
, i.e. as 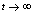
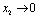 if
if 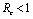 and
and 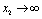 if
if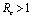 .Thus we can say that for
.Thus we can say that for 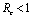 infective population decreases with time and after a sufficient large time disease will die out due to the unavailability of infected human.
infective population decreases with time and after a sufficient large time disease will die out due to the unavailability of infected human.
5. Endemic Equilibrium Point
Endemic equilibrium point is the steady state solution when the disease persists in the population i.e. 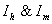 are positive. In the model (2.4), a unique endemic equilibrium point E1(
are positive. In the model (2.4), a unique endemic equilibrium point E1(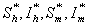 ), where
), where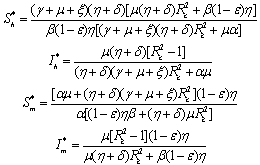 exists only when
exists only when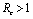 .
.
6. Stability of Endemic Equilibrium Point
Applying the transformations,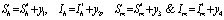 in (2.4)We have,
in (2.4)We have,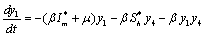 | (6.1a) |
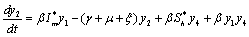 | (6.1b) |
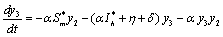 | (6.1c) |
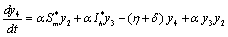 | (6.1d) |
6.1. Local Stability Analysis of Endemic Equilibrium Point
The linearized system of (2.4) around E1 is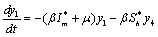 | (6.2a) |
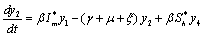 | (6.2b) |
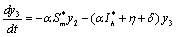 | (6.2c) |
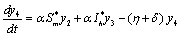 | (6.2d) |
The Jacobian of linearized system around E1 is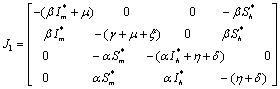 One characteristic root of
One characteristic root of 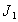 is -
is -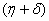 which is negative and remaining three characteristic roots are obtained by solving following cubic equation.
which is negative and remaining three characteristic roots are obtained by solving following cubic equation.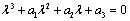 | (6.3) |
Where,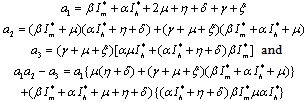 Since
Since 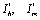 exists and are positive only when
exists and are positive only when , therefore
, therefore 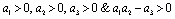 when
when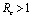 .Thus by Hurwitz criterion all the roots of (6.3) are either negative or have negative real parts if
.Thus by Hurwitz criterion all the roots of (6.3) are either negative or have negative real parts if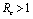 .Hence we have established the following result.Theorem 6.1. The endemic equilibrium point E1 exists and is locally asymptotically stable if
.Hence we have established the following result.Theorem 6.1. The endemic equilibrium point E1 exists and is locally asymptotically stable if 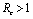 and it does not exist if
and it does not exist if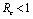 .
.
6.2. Non Linear Stability Analysis of Endemic Equilibrium Point
Consider a positive definite function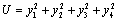 | (6.4) |
Then using the non-linear system (6.1) in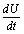 , we get
, we get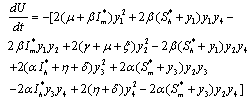 Now using the inequality,
Now using the inequality, 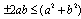 on the right hand side of
on the right hand side of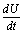 , we find that
, we find that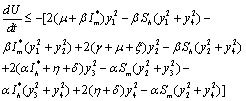 | (6.5) |
Again using the region 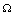 on the right hand side of the above inequality (6.5), we get
on the right hand side of the above inequality (6.5), we get 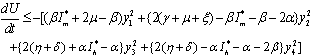 Thus,
Thus,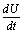 is negative definite if the following conditions hold good.
is negative definite if the following conditions hold good.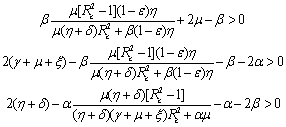 Hence, we have reached the following result.Theorem 6.2 The endemic equilibrium point E1 is non-linearly asymptotically stable if following conditions are being satisfied.(i)
Hence, we have reached the following result.Theorem 6.2 The endemic equilibrium point E1 is non-linearly asymptotically stable if following conditions are being satisfied.(i) 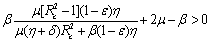 (ii)
(ii) 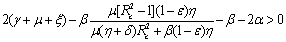 (iii)
(iii) 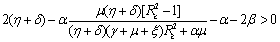
7. Discussion
In this paper, we have analyzed a model to study the impact of various vector control measures on the transmission dynamics of chikungunya disease. We have shown that there exists a feasible region where the model is well posed and for which a unique disease free equilibrium point is obtained. We defined a control reproductive number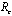 , and it has been concluded that DFE is linearly asymptotically stable if
, and it has been concluded that DFE is linearly asymptotically stable if 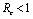 and unstable if
and unstable if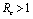 (Theorems 4.1&6.1). We have also shown that an endemic equilibrium point exists which is linearly asymptotically stable if
(Theorems 4.1&6.1). We have also shown that an endemic equilibrium point exists which is linearly asymptotically stable if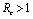 .When no vector control measure is applied then the control reproductive number
.When no vector control measure is applied then the control reproductive number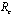 becomes the basic reproductive number
becomes the basic reproductive number 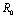 and it has been shown that
and it has been shown that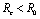 .Thus we have verified that the intervention policy by means of vector control, decreases the reproductive number and level of disease.Also the conditions for non linear stability of both the equilibrium points have been derived (Theorems 4.2 &6.2).The solution of linearized system (4.2) shows that the disease will die out after some time if
.Thus we have verified that the intervention policy by means of vector control, decreases the reproductive number and level of disease.Also the conditions for non linear stability of both the equilibrium points have been derived (Theorems 4.2 &6.2).The solution of linearized system (4.2) shows that the disease will die out after some time if 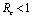 and it will remain in the population if
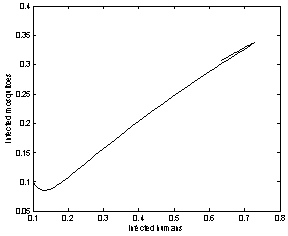
and it will remain in the population if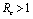 .Finally, with the help of simulations the graphs between state variables and time have been plotted (fig.2,3,4&5), and phase plane plots between Ih and Im have been also shown(fig.6,7,8 & 9) for different values of
.Finally, with the help of simulations the graphs between state variables and time have been plotted (fig.2,3,4&5), and phase plane plots between Ih and Im have been also shown(fig.6,7,8 & 9) for different values of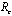 . It has been shown from the figures that if we are able to reduce the control reproductive number to less than 1 using various control measures independently or simultaneously then disease likely to vanish.
. It has been shown from the figures that if we are able to reduce the control reproductive number to less than 1 using various control measures independently or simultaneously then disease likely to vanish.Table 1. Parameter values and initial conditions used in the simulation
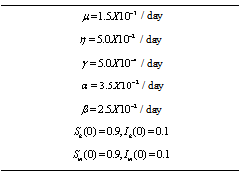 |
| |
|
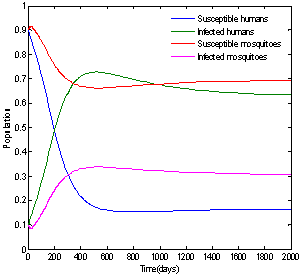 | Figure 2. Solution of chikungunya model without control measures and with parameter values given in table 1 which corresponds to Rc = 2.9580 |
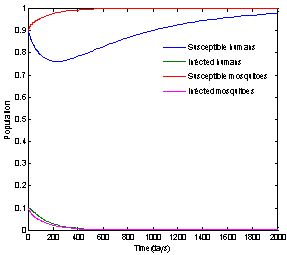 | Figure 3. Solution of chikungunya model with parameter values given in table 1 and with 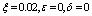 which corresponds to Rc = 0.8919 which corresponds to Rc = 0.8919 |
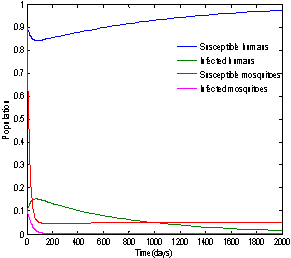 | Figure 4. Solution of chikungunya model with parameter values given in table 1 and with 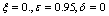 which corresponds to Rc = 0.6614 which corresponds to Rc = 0.6614 |
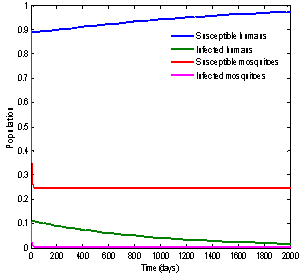 | Figure 5. Solution of chikungunya model with parameter values given in table 1 and with 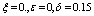 which corresponds to Rc = 0.7395 which corresponds to Rc = 0.7395 |
 | Figure 6. Phase plane plot between Ih and Im of chikungunya model without control measures and with parameter values given in table 1 which corresponds to Rc = 2.9580 |
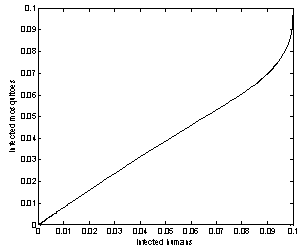 | Figure 7. Phase plane plot between Ih and Im of chikungunya model with parameter values given in table 1 and with 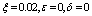 which corresponds to Rc = 0.8919 which corresponds to Rc = 0.8919 |
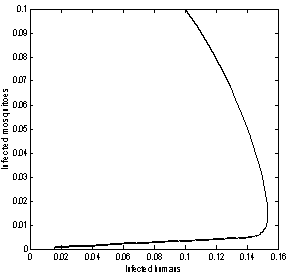 | Figure 8. Phase plane plot between Ih and Im of chikungunya model with parameter values given in table 1 and with 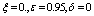 which corresponds to Rc = 0.6614 which corresponds to Rc = 0.6614 |
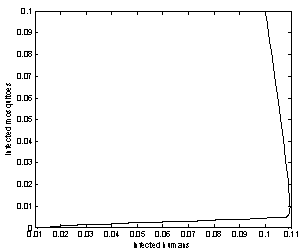 | Figure 9. Phase plane plot between Ih and Im of chikungunya model with parameter values given in table 1 and with 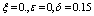 which corresponds to Rc = 0.7395 which corresponds to Rc = 0.7395 |
Table 2. Endemic values of state variables for parameter values given in table 1, where ξ = ε = δ=0
 |
| |
|
References
| [1] | Anderson R.M. and May R.M., Infectious Diseases of Humans: Dynamics and Control, Oxford University Press, Oxford, UK, 1991. |
| [2] | Aron J.L., Mathematical modeling of immunity to malaria, Math. Biosci., 90 (1988), 385-398. |
| [3] | Bailey N.T.J., The mathematical theory of infectious diseases and its application, Griffin London, 1975. |
| [4] | Bacaër Nicolas, Approximation of the basic reproduction number 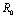 for vector borne diseases with a periodic vector population, Bull. Math. Biol., 69 (2008), 1067-1091. for vector borne diseases with a periodic vector population, Bull. Math. Biol., 69 (2008), 1067-1091. |
| [5] | Chitnis N., Cushing J.M. and Hyman J.M., Bifurcation analysis of a mathematical model for malaria transmission, SIAM J. Appl. Math., 67 (2006) 24-45. |
| [6] | Chitnis N., Hyman J.M.and Cushing J.M., Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model, Bull. Math. Biol., 70 (2008) 1272-1296. |
| [7] | Diekmann. O and Heesterbeek J.A.P., Mathematical Epidemiology of Infectious Diseases, Wiley, New York, 2000. |
| [8] | Diekmann O., Heesterbeek J.A.P. and Metz J.A.J., On the definition and the computation of the basic reproduction ratio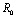 in models for infectious diseases in heterogeneous populations, J. Math. Biol., 28 (1990) 365-382. in models for infectious diseases in heterogeneous populations, J. Math. Biol., 28 (1990) 365-382. |
| [9] | Esteva L. and Vargas C., Analysis of a dengue disease transmission model, Math. Biosci, 150 (1998) 131-115. |
| [10] | Esteva L. and Vargas C., A model for dengue disease with variable human population, J. Math. Biol., 38 (1999) 220-240. |
| [11] | Heffernan J.M., Smith R.J. and Wahl L.M., Perspectives on the Basic Reproductive ratio, Journal of The Royal society interface, 2 (2005) 281-293. |
| [12] | Park K., Preventive and Social Medicine, M/S Banarsi Das Bhanot Publishers, Jabalpur, India, 2005. |
| [13] | Ramchurn, S.K.,Goorah S.S.D., Mungla D., Ramsurrun B., Pydiah and Summun A., A study of the 2006 Chikungunya epidemic outbreak in Mauritius, Internet Journal of Medical Update, 3 (2008) 11-21. |
| [14] | World Health Organization, Chikungunya Fever fact sheet, (2008),http://www.searo.who.int/LinkFiles/Chikungunya_fever_fact_sheet.pdf. |
| [15] | Yadav J.S., A special issue on Chikungunya, ENVIS News Letter, 3 (2006) 1-12. |
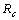 , and we have found that the disease free equilibrium point is locally asymptotically stable when
, and we have found that the disease free equilibrium point is locally asymptotically stable when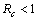 and unstable when
and unstable when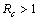 .We have also proved that a unique endemic equilibrium point exists and is locally asymptotically stable when
.We have also proved that a unique endemic equilibrium point exists and is locally asymptotically stable when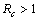 . Thus, we have concluded from the analysis of the model that the disease will either die out or will remain endemic depending on the value of control reproductive number. This study will assist the health department in controlling the spread of Chikungunya disease by introducing the control measures such as increasing the awareness in the society, killing of mosquitoes and isolating the infected individuals.
. Thus, we have concluded from the analysis of the model that the disease will either die out or will remain endemic depending on the value of control reproductive number. This study will assist the health department in controlling the spread of Chikungunya disease by introducing the control measures such as increasing the awareness in the society, killing of mosquitoes and isolating the infected individuals.

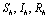 are the proportions of the susceptible, infectious and removed individuals in the human population and
are the proportions of the susceptible, infectious and removed individuals in the human population and 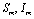 are the proportions of the susceptible and infected mosquitoes in the mosquito population. The dynamical system representing the epidemic spread in human and vector population are then given by the following system of non linear ordinary differential equations.
are the proportions of the susceptible and infected mosquitoes in the mosquito population. The dynamical system representing the epidemic spread in human and vector population are then given by the following system of non linear ordinary differential equations.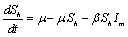
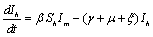
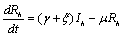
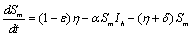
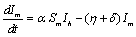
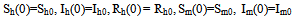
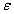 = Rate of awareness programme for reducing vector breeding. (
= Rate of awareness programme for reducing vector breeding. (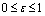 ).δ = Killing rate of mosquitoes by spraying chemicals. Let
).δ = Killing rate of mosquitoes by spraying chemicals. Let 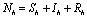 and
and 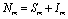 are total population sizes of human and mosquitoes respectively. Then
are total population sizes of human and mosquitoes respectively. Then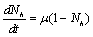
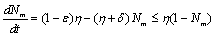
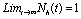 and
and 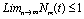 It can be easily seen that the feasible region
It can be easily seen that the feasible region 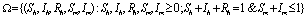 is positively invariant for the model(2.1).Thus, we restrict our attention to the dynamics of the model in
is positively invariant for the model(2.1).Thus, we restrict our attention to the dynamics of the model in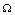 .Using
.Using 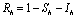 in
in 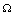 equation(2.1c) can be removed from the model. Therefore we have to study only following four equations.
equation(2.1c) can be removed from the model. Therefore we have to study only following four equations.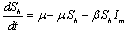
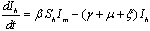
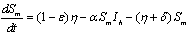
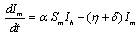
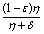 , 0) in the region
, 0) in the region 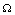 , with no disease in the population.We use the next generation matrix approach as described by Diekmann et. al[8] and Hefferman et. al[11] to define the reproductive number
, with no disease in the population.We use the next generation matrix approach as described by Diekmann et. al[8] and Hefferman et. al[11] to define the reproductive number 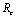 which we call control reproductive number, as the number of secondary infections that one infectious individual would create over the duration of the infectious period in the presence of control measures, provided that everyone else is susceptible. For the model (2.4)
which we call control reproductive number, as the number of secondary infections that one infectious individual would create over the duration of the infectious period in the presence of control measures, provided that everyone else is susceptible. For the model (2.4)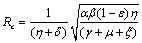
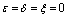 . In this condition the control reproductive number become basic reproductive number
. In this condition the control reproductive number become basic reproductive number 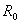 and
and 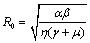
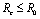 .
.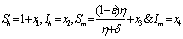 in (2.4) we have,
in (2.4) we have,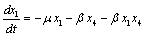
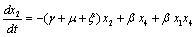
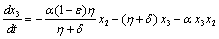
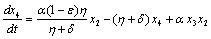
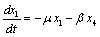
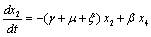
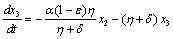
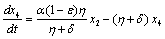
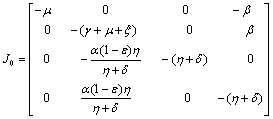 Two characteristic roots of
Two characteristic roots of 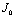 are -
are -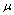 and -
and -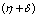 which are negative and remaining two characteristic roots are obtained by solving quadratic equation.
which are negative and remaining two characteristic roots are obtained by solving quadratic equation.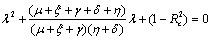
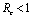 and has exactly one positive root if
and has exactly one positive root if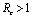 .Thus we have established the following result.Theorem 4.1. The disease free equilibrium point E0 is locally asymptotically stable if
.Thus we have established the following result.Theorem 4.1. The disease free equilibrium point E0 is locally asymptotically stable if 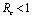 and unstable if
and unstable if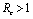 .
.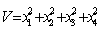
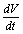 , we get
, we get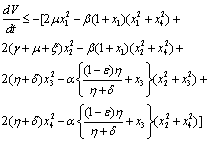 Now using the inequality
Now using the inequality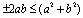 on the right hand side of
on the right hand side of 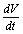 we find that
we find that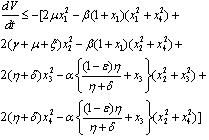
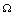 on the right hand side of the above inequality (4.1) we get
on the right hand side of the above inequality (4.1) we get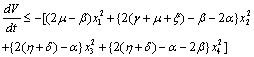 Now, it can be easily seen that
Now, it can be easily seen that 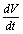 is negative definite under the following conditions.
is negative definite under the following conditions.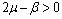
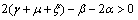
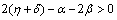
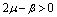 (ii)
(ii) 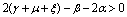 (iii)
(iii) 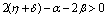 To predict the behaviour of
To predict the behaviour of  we have solved the linearized system (4.2) around E0.From equations (4.2b) and (4.2d) we get
we have solved the linearized system (4.2) around E0.From equations (4.2b) and (4.2d) we get 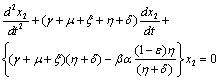
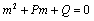
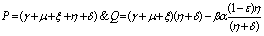 If two roots of (4.7) are
If two roots of (4.7) are 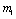 and
and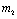 then,
then, 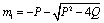 and
and 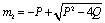 Since
Since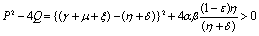 Therefore both the roots of (4.8) are real. Root
Therefore both the roots of (4.8) are real. Root 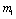 is always negative and
is always negative and 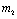 is negative if
is negative if 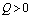 and positive if
and positive if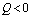 .Again
.Again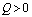
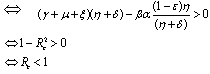 Thus
Thus 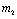 is negative if
is negative if 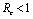 and is positive if
and is positive if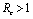 .Now solution of (4.7) is
.Now solution of (4.7) is 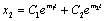 (4.9)Where,
(4.9)Where, 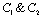 are constants of integration. Now if
are constants of integration. Now if 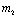 is negative then
is negative then 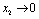 as
as 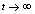 and if
and if 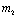 is positive then
is positive then 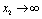 as
as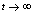 , i.e. as
, i.e. as 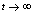
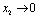 if
if 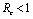 and
and 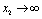 if
if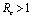 .Thus we can say that for
.Thus we can say that for 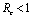 infective population decreases with time and after a sufficient large time disease will die out due to the unavailability of infected human.
infective population decreases with time and after a sufficient large time disease will die out due to the unavailability of infected human.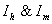 are positive. In the model (2.4), a unique endemic equilibrium point E1(
are positive. In the model (2.4), a unique endemic equilibrium point E1(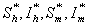 ), where
), where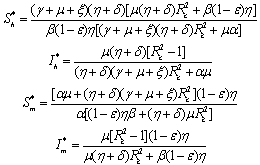 exists only when
exists only when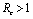 .
.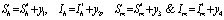 in (2.4)We have,
in (2.4)We have,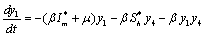
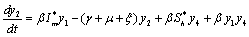
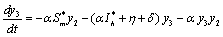
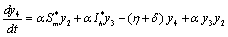
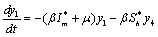
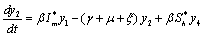
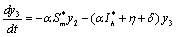
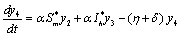
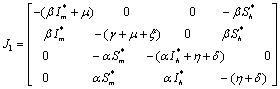 One characteristic root of
One characteristic root of 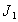 is -
is -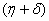 which is negative and remaining three characteristic roots are obtained by solving following cubic equation.
which is negative and remaining three characteristic roots are obtained by solving following cubic equation.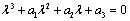
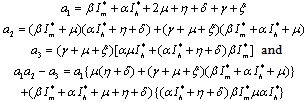 Since
Since 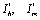 exists and are positive only when
exists and are positive only when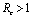 , therefore
, therefore 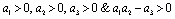 when
when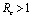 .Thus by Hurwitz criterion all the roots of (6.3) are either negative or have negative real parts if
.Thus by Hurwitz criterion all the roots of (6.3) are either negative or have negative real parts if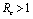 .Hence we have established the following result.Theorem 6.1. The endemic equilibrium point E1 exists and is locally asymptotically stable if
.Hence we have established the following result.Theorem 6.1. The endemic equilibrium point E1 exists and is locally asymptotically stable if 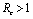 and it does not exist if
and it does not exist if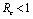 .
.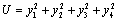
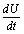 , we get
, we get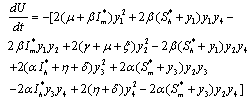 Now using the inequality,
Now using the inequality, 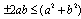 on the right hand side of
on the right hand side of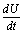 , we find that
, we find that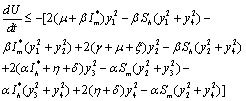
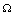 on the right hand side of the above inequality (6.5), we get
on the right hand side of the above inequality (6.5), we get 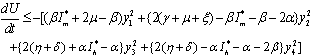 Thus,
Thus,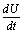 is negative definite if the following conditions hold good.
is negative definite if the following conditions hold good.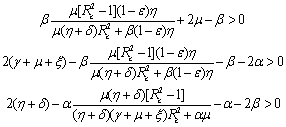 Hence, we have reached the following result.Theorem 6.2 The endemic equilibrium point E1 is non-linearly asymptotically stable if following conditions are being satisfied.(i)
Hence, we have reached the following result.Theorem 6.2 The endemic equilibrium point E1 is non-linearly asymptotically stable if following conditions are being satisfied.(i) 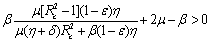 (ii)
(ii) 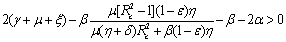 (iii)
(iii) 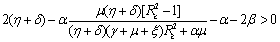
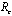 , and it has been concluded that DFE is linearly asymptotically stable if
, and it has been concluded that DFE is linearly asymptotically stable if 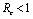 and unstable if
and unstable if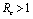 (Theorems 4.1&6.1). We have also shown that an endemic equilibrium point exists which is linearly asymptotically stable if
(Theorems 4.1&6.1). We have also shown that an endemic equilibrium point exists which is linearly asymptotically stable if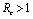 .When no vector control measure is applied then the control reproductive number
.When no vector control measure is applied then the control reproductive number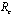 becomes the basic reproductive number
becomes the basic reproductive number 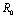 and it has been shown that
and it has been shown that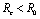 .Thus we have verified that the intervention policy by means of vector control, decreases the reproductive number and level of disease.Also the conditions for non linear stability of both the equilibrium points have been derived (Theorems 4.2 &6.2).The solution of linearized system (4.2) shows that the disease will die out after some time if
.Thus we have verified that the intervention policy by means of vector control, decreases the reproductive number and level of disease.Also the conditions for non linear stability of both the equilibrium points have been derived (Theorems 4.2 &6.2).The solution of linearized system (4.2) shows that the disease will die out after some time if 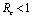 and it will remain in the population if
and it will remain in the population if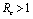 .Finally, with the help of simulations the graphs between state variables and time have been plotted (fig.2,3,4&5), and phase plane plots between Ih and Im have been also shown(fig.6,7,8 & 9) for different values of
.Finally, with the help of simulations the graphs between state variables and time have been plotted (fig.2,3,4&5), and phase plane plots between Ih and Im have been also shown(fig.6,7,8 & 9) for different values of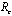 . It has been shown from the figures that if we are able to reduce the control reproductive number to less than 1 using various control measures independently or simultaneously then disease likely to vanish.
. It has been shown from the figures that if we are able to reduce the control reproductive number to less than 1 using various control measures independently or simultaneously then disease likely to vanish.

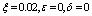 which corresponds to Rc = 0.8919
which corresponds to Rc = 0.8919
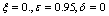 which corresponds to Rc = 0.6614
which corresponds to Rc = 0.6614
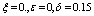 which corresponds to Rc = 0.7395
which corresponds to Rc = 0.7395

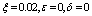 which corresponds to Rc = 0.8919
which corresponds to Rc = 0.8919
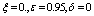 which corresponds to Rc = 0.6614
which corresponds to Rc = 0.6614
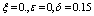 which corresponds to Rc = 0.7395
which corresponds to Rc = 0.7395 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML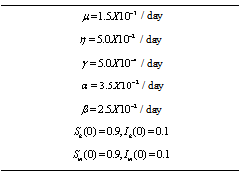

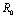 for vector borne diseases with a periodic vector population, Bull. Math. Biol., 69 (2008), 1067-1091.
for vector borne diseases with a periodic vector population, Bull. Math. Biol., 69 (2008), 1067-1091.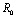 in models for infectious diseases in heterogeneous populations, J. Math. Biol., 28 (1990) 365-382.
in models for infectious diseases in heterogeneous populations, J. Math. Biol., 28 (1990) 365-382.