Rajesh C. Shah 1, Dilip B. Patel 2
1Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara - 390 001, Gujarat State, India
2Department of Mathematics, Sankalchand Patel College of Engineering, Visnagar – 384 315, Gujarat State, India
Correspondence to: Rajesh C. Shah , Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara - 390 001, Gujarat State, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper theoretically studied the effects of various porous structure on the action of the squeeze film formed when a curved upper plate with porous facing approached an impermeable and flat lower plate using ferrofluid as lubricant. Two porous structures given by Kozeny - Carman( a globular sphere model ) and Irmay ( a capillary fissures model ) are considered for the study. Expressions are obtained for pressure and load capacity under an external magnetic field oblique the lower plate. It is found that the load capacity is increased in both the cases with the increase of magnetization. It is also found that the load capacity increased substantially in the case of concave plates and in the case of porous structure given by Kozeny - Carman. The load capacity is more for the porous structure given by Kozeny – Carman.
Keywords:
Ferrofluid, Squeeze Film, Porous, Circular Plates, Lubrication
1. Introduction
Ferrofluid or magnetic fluid[1] are stable colloidal suspensions containing fine ferromagnetic particles dispersing in a liquid, called carrier liquid, in which a surfactant is added to generate a coating layer preventing the flocculation of the particles. When an external magnetic field is applied, ferrofluids experience magnetic body forces depends upon the magnetization of ferromagnetic particles. Owing to these features ferrofluids are useful in many applications like in sensors, sealing devices, filtering apparatus, etc.[2,3].Wu[4], in an innovative analysis , dealt with the case of squeeze film behavior for porous annular disks in which he showed that owing to the fact that fluid can flow through the porous material as well as through the space between the bounding surfaces , the performance of a porous walled squeeze film can differ substantially from that of a solid walled squeeze film. Murti[5] analyzed the squeeze film behavior between porous circular discs.With the advent of ferrofluid, Agrawal[6] studied its effects on a porous inclined bearing and found that the magnetization of the magnetic particles in the lubricant increased its load capacity without affecting the friction on the moving slider. Later Verma[7] and Shah and Bhat[8,9] investigated the squeeze film between porous plates and found that its performance with magnetic fluid lubricant was better than with conventional lubricant.In all above investigations, none of the authors considered various porous structure for porous plates in their study. The porous layer in the bearing is considered because its advantages property of self lubrication. With this motivation, we recapitulate the study of the paper of Shah and Bhat[10] for various porous structure without the effect of rotation, and with the effect of ferrofluid as lubricant under a magnetic field oblique to the lower plate. The problem also include the effect of squeeze velocity and the curvature of the upper disc. The ferrofluid flow model considered here is due to R. E. Rosensweig[1].A ferrofluid lubrication equation is derived for the above problem and the various porous structure is considered for computation of bearing characteristics like pressure and load capacity. The ferrofluid used in computations are water based.
2. The Mathematical Model
The configuration of the bearing, shown in Figure 1, consists of two circular plates each of radius a (metre). The upper plate has a porous facing of thickness l1(metre) which is backed by a solid wall. It moves normally towards an impermeable and flat lower plate with uniform velocity 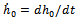 where
where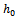 (metre) is the central film thickness and t is time in seconds. The film thickness h (metre) is given by
(metre) is the central film thickness and t is time in seconds. The film thickness h (metre) is given by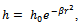 | (1) |
where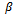 is the curvature of the upper plate and r (metre) is the radial coordinate.Assuming axially symmetric flow of the ferrofluid between the plates under an oblique magnetic field
is the curvature of the upper plate and r (metre) is the radial coordinate.Assuming axially symmetric flow of the ferrofluid between the plates under an oblique magnetic field 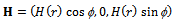 whose magnitude H vanishes at
whose magnitude H vanishes at 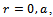 the modified Reynolds’s equation governing the film pressure p is[10]
the modified Reynolds’s equation governing the film pressure p is[10]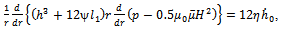 | (2) |
where 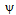 is the permeability of the porous region,
is the permeability of the porous region, 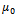 is the permeability of the free space,
is the permeability of the free space, 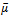 is the magnetic susceptibility and
is the magnetic susceptibility and 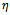 is the fluid viscosity.
is the fluid viscosity.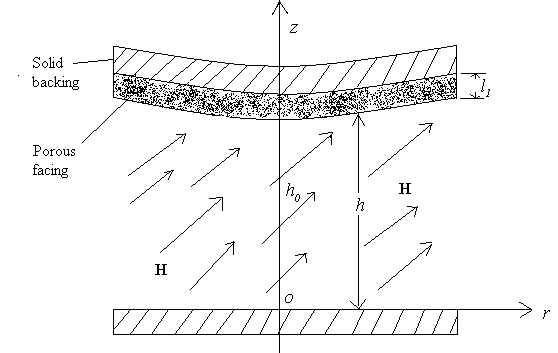 | Figure 1. Configuration of the problem |
3. Solution
CASE I (a globular sphere model as shown in Figure 2). A porous material is filled with globular particles ( a mean particle size 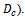
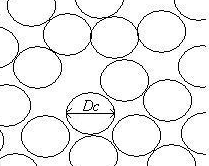 | Figure 2. Structure model of porous sheets given by Kozeny-Carman |
In this case Kozeny-Carman formula[11] gives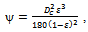 | (3) |
where 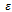 is the porosity.Let us introduce the dimensionless quantities
is the porosity.Let us introduce the dimensionless quantities 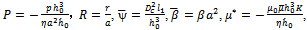 | (4) |
and take, for example,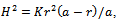 | (5) |
where 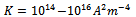 is chosen so as to have a magnetic field of strength between the order of 105 to 106.The angle
is chosen so as to have a magnetic field of strength between the order of 105 to 106.The angle 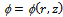 ,since the magnetic field arise out of a potential, can be determined from
,since the magnetic field arise out of a potential, can be determined from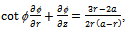 | (6) |
with the help of elliptic integrals depending on the value of 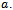 Using equations (1) - (5), we see that the dimensionless film pressure P satisfies the equation
Using equations (1) - (5), we see that the dimensionless film pressure P satisfies the equation 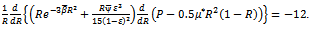 | (7) |
Solving equation (7) under the boundary conditions 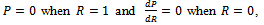 | (8) |
we obtain 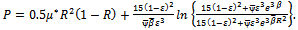 | (9) |
The load capacity W of the bearing can be expressed in dimensionless form as 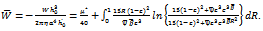 | (10) |
CASE II (a capillary fissures model as shown Figure 3). The model is composed of three sets of mutually orthogonal fissures (a mean solid size 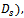 and assuming no loss of hydraulic gradient at the junctions, Irmay[12] derived the permeability
and assuming no loss of hydraulic gradient at the junctions, Irmay[12] derived the permeability | Figure 3. Structure model of porous sheets given by Irmay |
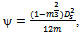 | (11) |
where 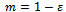 and
and 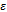 is the porosityLet us introduce the dimensionless quantities
is the porosityLet us introduce the dimensionless quantities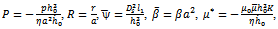 | (12) |
Using equations(1), (2), (5), (11) and (12), the dimensionless film pressure P satisfies the equation 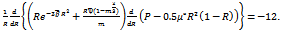 | (13) |
Solving equation (13) under the boundary conditions (8), we obtain 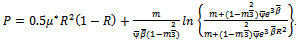 | (14) |
The load capacity W of the bearing can be expressed in dimensionless form as 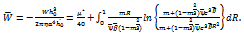 | (15) |
4. Results and Discussion
The dimensionless pressure P and load capacity 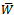 are given, by equations (9), (10) for globular sphere model given by Kozeny-Carman and by equations (14), (15) for capillary fissures model by Irmay.Setting the magnetization parameter
are given, by equations (9), (10) for globular sphere model given by Kozeny-Carman and by equations (14), (15) for capillary fissures model by Irmay.Setting the magnetization parameter 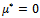 and without considering the two cases of
and without considering the two cases of 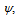 the present analysis reduces to nonmagnetic case[13].Also, setting
the present analysis reduces to nonmagnetic case[13].Also, setting 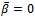 in equations (9), (10) and (14), (15), we obtain the results for flat upper plate for two cases.The computed values of the dimensionless load capacity
in equations (9), (10) and (14), (15), we obtain the results for flat upper plate for two cases.The computed values of the dimensionless load capacity 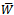 are displayed in figure 4 and figure 5 for two different cases and for the following value of the parameters:
are displayed in figure 4 and figure 5 for two different cases and for the following value of the parameters: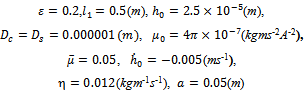 Figure 4 and figure 5 show that
Figure 4 and figure 5 show that 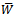 increase with
increase with 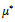 and
and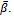 The increases are substantial in the case of concave plates
The increases are substantial in the case of concave plates 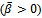 for case I.
for case I.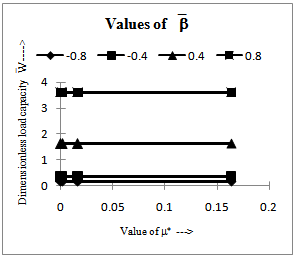 | Figure 4. Values of the dimensionless load capacity  for different values of for different values of  and and 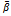 for case I for case I |
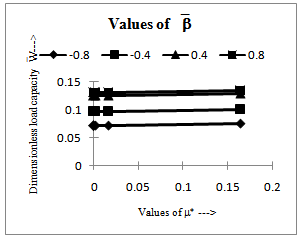 | Figure 5. Values of the dimensionless load capacity 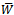 for different values of for different values of 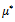 and and 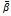 for case II for case II |
The load capacity also increases more in case I, this may be because of the slow coming out of the ferrofluid from the porous region.
5. Conclusions
Based upon the results and discussion it can be concluded that the better load carrying capacity is obtained for globular sphere model with the effect of ferrofluid under an oblique magnetic field to the lower plate.Thus, it is suggested to have a design of porous squeeze bearing with globular sphere in the porous region.
References
| [1] | R E Rosensweig. Ferrohydrodynamics, Cambridge University Press, New York (1985). |
| [2] | N C Popa, I Potencz, L Brostean, L Vekas. Some applications of inductive transducers with magnetic fluids, Sensors and Actuators A , 59 (1997) 197-200. |
| [3] | M Goldowsky. New methods for sealing, filtering, and lubricating with magnetic fluids, IEEE transactions on Magnetics, Mag.- 16 (1980) 382-386. |
| [4] | H Wu. Squeeze- film behavior for porous annular disks, Journal of Lubrication Technology, Trans. ASME, Series F, 92(4) (1970) 593-596. |
| [5] | P R K Murti. Squeeze-film behavior in porous circular discs, Journal of Lubrication Technology, 96(1974) 206. |
| [6] | V K Agrawal. Magnetic fluid based porous inclined slider bearing, Wear,107 (1986) 133-139. |
| [7] | P D S Verma. Magnetic fluid based squeeze film,International Journal of Engineering Science, 24(1986) 395. |
| [8] | R C Shah, S R Tripathi, M V Bhat. Magnetic fluid based squeeze film between porous annular curved plates with the effect of rotational inertia, Pramana- Journal of Physics, 58(3) (2002) 545-550. |
| [9] | R C Shah, M V Bhat. Combined effect of anisotropic permeability and slip velocity on porous walled squeeze films lubricated with a ferrofluid, Journal of Friction and Wear, 24(1),(2003) 58-64. |
| [10] | R C Shah, M V Bhat. Squeeze film based on magnetic fluid in curved porous rotating circular plates, Journal of Magnetism and Magnetic Materials,208 (2000) 115-119. |
| [11] | Jun Liu. Analysis of a porous elastic sheet damper with a magnetic fluid, Journal of Tribology, 131(2009) 0218011-15. |
| [12] | S Irmay. Flow of liquid through cracked media, Bull. Res. Counc. Isr., 5A(1)(1955) 84. |
| [13] | M V Bhat, J V Hingu. Squeeze films in curved porous circular plates, Wear 52(1979) 193 |

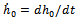 where
where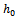 (metre) is the central film thickness and t is time in seconds. The film thickness h (metre) is given by
(metre) is the central film thickness and t is time in seconds. The film thickness h (metre) is given by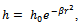
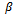 is the curvature of the upper plate and r (metre) is the radial coordinate.Assuming axially symmetric flow of the ferrofluid between the plates under an oblique magnetic field
is the curvature of the upper plate and r (metre) is the radial coordinate.Assuming axially symmetric flow of the ferrofluid between the plates under an oblique magnetic field 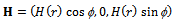 whose magnitude H vanishes at
whose magnitude H vanishes at 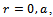 the modified Reynolds’s equation governing the film pressure p is[10]
the modified Reynolds’s equation governing the film pressure p is[10]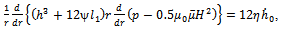
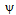 is the permeability of the porous region,
is the permeability of the porous region, 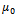 is the permeability of the free space,
is the permeability of the free space, 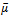 is the magnetic susceptibility and
is the magnetic susceptibility and 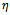 is the fluid viscosity.
is the fluid viscosity.
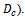

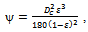
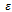 is the porosity.Let us introduce the dimensionless quantities
is the porosity.Let us introduce the dimensionless quantities 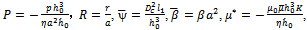
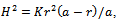
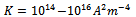 is chosen so as to have a magnetic field of strength between the order of 105 to 106.The angle
is chosen so as to have a magnetic field of strength between the order of 105 to 106.The angle 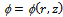 ,since the magnetic field arise out of a potential, can be determined from
,since the magnetic field arise out of a potential, can be determined from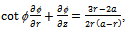
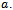 Using equations (1) - (5), we see that the dimensionless film pressure P satisfies the equation
Using equations (1) - (5), we see that the dimensionless film pressure P satisfies the equation 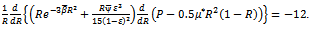
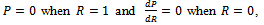
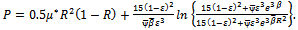
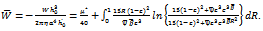
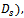 and assuming no loss of hydraulic gradient at the junctions, Irmay[12] derived the permeability
and assuming no loss of hydraulic gradient at the junctions, Irmay[12] derived the permeability
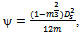
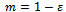 and
and 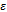 is the porosityLet us introduce the dimensionless quantities
is the porosityLet us introduce the dimensionless quantities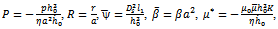
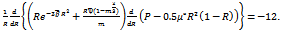
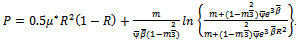
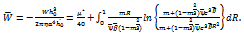
 are given, by equations (9), (10) for globular sphere model given by Kozeny-Carman and by equations (14), (15) for capillary fissures model by Irmay.Setting the magnetization parameter
are given, by equations (9), (10) for globular sphere model given by Kozeny-Carman and by equations (14), (15) for capillary fissures model by Irmay.Setting the magnetization parameter 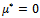 and without considering the two cases of
and without considering the two cases of  the present analysis reduces to nonmagnetic case[13].Also, setting
the present analysis reduces to nonmagnetic case[13].Also, setting 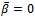 in equations (9), (10) and (14), (15), we obtain the results for flat upper plate for two cases.The computed values of the dimensionless load capacity
in equations (9), (10) and (14), (15), we obtain the results for flat upper plate for two cases.The computed values of the dimensionless load capacity 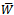 are displayed in figure 4 and figure 5 for two different cases and for the following value of the parameters:
are displayed in figure 4 and figure 5 for two different cases and for the following value of the parameters: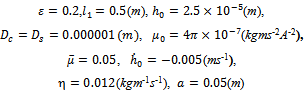 Figure 4 and figure 5 show that
Figure 4 and figure 5 show that 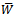 increase with
increase with 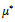 and
and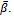 The increases are substantial in the case of concave plates
The increases are substantial in the case of concave plates 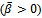 for case I.
for case I.
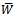 for different values of
for different values of 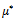 and
and 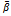 for case I
for case I
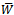 for different values of
for different values of 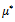 and
and 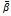 for case II
for case II Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML