-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(4): 116-120
doi: 10.5923/j.am.20120204.03
Interval – Valued Differential Equations with Generalized Derivative
Natalia Skripnik
Department of Optimal Control & Economic Cybernetics, Odessa National University named after I.I. Mechnikov, Odessa, 65026, Ukraine
Correspondence to: Natalia Skripnik , Department of Optimal Control & Economic Cybernetics, Odessa National University named after I.I. Mechnikov, Odessa, 65026, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper the concept of generalized differentiability (proposed in[17]) for interval-valued mappings is used. The interval-valued differential equations with generalized derivative are considered and the existence theorem is proved.
Keywords: Interval-valued Mapping, Generalized Derivative, Differential Equations, Existence Theorem
Article Outline
1. Introduction
- Lately the development of calculus in metric spaces became an object of attention of many researchers [1,11-14,16,18 and ref. herein]. Earlier F.S. de Blasi and F. Iervolino begun studying of set-valued differential equations (SDEs) in semilinear metric spaces[5-8]. Now it transformed into the theory of SDEs as an independent discipline. The properties of solutions, the impulse SDEs, control systems and asymptotic methods for SDEs were considered. On the other hand, SDEs are useful in other areas of mathematics. For example, SDEs are used as an auxiliary tool to prove the existence results for differential inclusions. Also, one can employ SDEs in the investigation of fuzzy differential equations. Moreover, SDEs are a natural generalization of usual ordinary differential equations in finite (or infinite) dimensional Banach spaces.However all these equations have a natural lack - the diameter of a set-valued solution is a non-decreasing function. Possibly it is connected with the fact that these differential equations were entered by analogy with the single-valued theory.But in the theory of ordinary differential equations a solution in any moment of time is a point (so a solution does not possess the property of "thickness"). Therefore, the similar introduction of the differential equations for a set-valued case is not absolutely adequate.In[17] a new concept of a derivative of a set-valued mapping that generalizes the concept of Hukuhara derivative was entered and a new type of a set-valued differential equation such that the diameter of its solution can whether increase or decrease (for example, to be periodic) was considered. In the ideological sense this definition of the derivative is close to the definitions proposed in[2-4,15].In this paper the interval-valued differential equations with generalized derivative are considered and the existence theorem is proved.
2. The Generalized Derivative
- Let
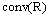 be a space of all nonempty closed intervals
be a space of all nonempty closed intervals 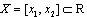 with Hausdorff metric
with Hausdorff metric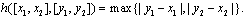 Definition 1 [10]. Let
Definition 1 [10]. Let 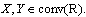 A set
A set 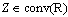 such that
such that 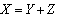 is called a Hukuhara difference of the sets X and Y and is denoted by
is called a Hukuhara difference of the sets X and Y and is denoted by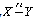 .Let
.Let 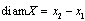 The Hukuhara difference of the sets
The Hukuhara difference of the sets 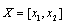 and
and 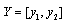 exists iff
exists iff 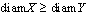 and is equal to
and is equal to 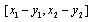 Let
Let 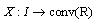 be an interval-valued mapping;
be an interval-valued mapping; 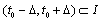 be a
be a 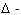 neighbourhood of a point
neighbourhood of a point 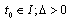
 | (1) |
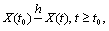 | (2) |
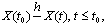 | (3) |
 | (4) |
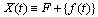 for
for 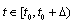 or
or 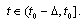 If all differences (1) - (4) exist then
If all differences (1) - (4) exist then 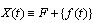 in
in 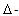 neighbourhood of the point
neighbourhood of the point 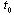 If for all
If for all 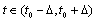 there exists only one of the one-sided differences, then using the properties of the Hukuhara difference, we get that the mapping
there exists only one of the one-sided differences, then using the properties of the Hukuhara difference, we get that the mapping 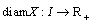 in the
in the 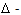 neighbourhood of the point
neighbourhood of the point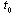 can be:a) non-decreasing on
can be:a) non-decreasing on 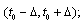 b) non-increasing on
b) non-increasing on 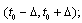 c) non-decreasing on
c) non-decreasing on 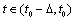 and non-increasing on
and non-increasing on 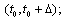 d) non-increasing on
d) non-increasing on 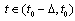 and non-decreasing on
and non-decreasing on 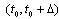 Hence, for each of the above mentioned cases only one of combinations of differences is possible:a) (1) and (3); b) (2) and (4); c) (2) and (3); d) (1) and (4).Consider four types of limits corresponding to one of the difference types:
Hence, for each of the above mentioned cases only one of combinations of differences is possible:a) (1) and (3); b) (2) and (4); c) (2) and (3); d) (1) and (4).Consider four types of limits corresponding to one of the difference types: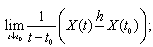 | (5) |
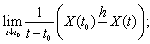 | (6) |
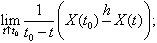 | (7) |
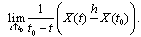 | (8) |
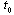 not more than two limits can exist (as we assumed that there exist only two of four Hukuhara differences).Considering all above we have that there exist only following combinations of limits:a) (5) and (7); b) (6) and (8); c) (6) and (7); d) (5) and (8).Definition 2. If the corresponding two limits exist and are equal we will say that the mapping
not more than two limits can exist (as we assumed that there exist only two of four Hukuhara differences).Considering all above we have that there exist only following combinations of limits:a) (5) and (7); b) (6) and (8); c) (6) and (7); d) (5) and (8).Definition 2. If the corresponding two limits exist and are equal we will say that the mapping 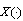 is differentiable in the generalized sense in the point
is differentiable in the generalized sense in the point 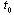 and denote the generalized derivative by
and denote the generalized derivative by 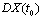 Let us say that the interval-valued mapping
Let us say that the interval-valued mapping 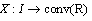 is differentiable in the generalized sense on the interval I if it is differentiable in the generalized sense at every point of this interval.Definition 3. The interval-valued mapping
is differentiable in the generalized sense on the interval I if it is differentiable in the generalized sense at every point of this interval.Definition 3. The interval-valued mapping 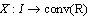 is called absolutely continuous on the interval I if there exist a measurable interval-valued mapping
is called absolutely continuous on the interval I if there exist a measurable interval-valued mapping 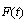 and a system of intervals
and a system of intervals 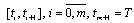 such that for all
such that for all 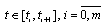

3. Differential Equations with the Generalized Derivative
- Consider the differential equation with the generalized derivative
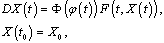 | (9) |
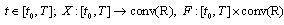
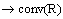 are interval valued mappings;
are interval valued mappings; 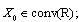
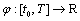 is a continuous function, function
is a continuous function, function 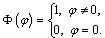 Definition 4. An interval-valued mapping
Definition 4. An interval-valued mapping 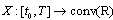 is called the solution of differential equation (9) if it is absolutely continuous, satisfies (9) almost everywhere on
is called the solution of differential equation (9) if it is absolutely continuous, satisfies (9) almost everywhere on 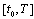 and
and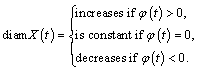 If on the interval
If on the interval 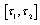 the function
the function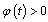 , then we have
, then we have  and
and 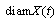 increases. So
increases. So 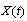 satisfies the integral equation
satisfies the integral equation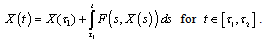 If on the interval
If on the interval 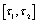 the function
the function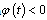 , then we have
, then we have 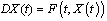 and
and 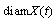 decreases. Therefore
decreases. Therefore 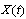 satisfies the integral equation i.e.
satisfies the integral equation i.e.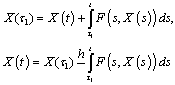 If on the interval
If on the interval 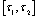 the function
the function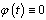 , then we have
, then we have 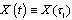 .Example 1. Consider the following differential equation with generalized derivative
.Example 1. Consider the following differential equation with generalized derivative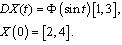 As
As 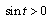 for
for 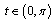 we have
we have 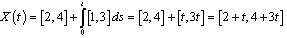 for
for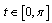 . So for
. So for 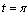 we get
we get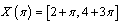 .Further as
.Further as  for
for 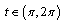 we have
we have 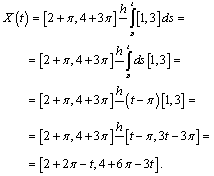 So for
So for 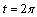 we get
we get . If we consider this equation for
. If we consider this equation for 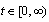 we will get the periodic solution.Example 2. Consider the same differential equation with generalized derivative but with
we will get the periodic solution.Example 2. Consider the same differential equation with generalized derivative but with :
: 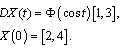 As
As 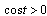 for
for 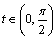 then we have
then we have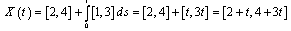 for
for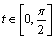 .Further as
.Further as 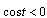 for
for 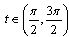 then we get
then we get 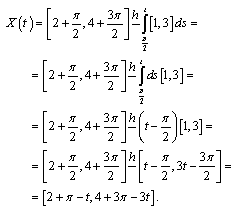 So for
So for 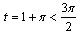 we have
we have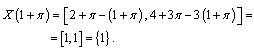 It means that the solution exists only for
It means that the solution exists only for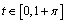 . Remark. It is obvious that the mapping
. Remark. It is obvious that the mapping 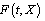 defines only on “how much” the interval-valued mapping
defines only on “how much” the interval-valued mapping 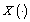 changes in case of its "decrease" or "increase" and function
changes in case of its "decrease" or "increase" and function 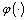 defines what will be with
defines what will be with 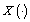 ["decrease" or "increase"]. If
["decrease" or "increase"]. If 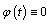 irrespective of
irrespective of 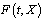 the mapping
the mapping 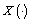 will be constant.Example 3. Consider the differential equation from Example 1 with
will be constant.Example 3. Consider the differential equation from Example 1 with 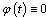 for
for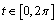 . Then
. Then 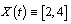 for
for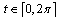 .If we take
.If we take 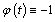 then we will have
then we will have 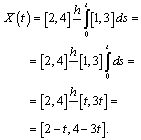 Then for
Then for 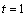 we get
we get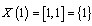 . So the solution exists for
. So the solution exists for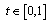 .So for all
.So for all 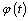 we can guarantee the existence of solution of the differential equation
we can guarantee the existence of solution of the differential equation 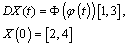 on the interval
on the interval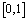 . Obviously, for example if
. Obviously, for example if 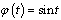 the solution exists on
the solution exists on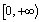 .The following theorem of existence of the solution of equation (9) holds:Theorem 1. Let the interval-valued mapping
.The following theorem of existence of the solution of equation (9) holds:Theorem 1. Let the interval-valued mapping 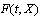 in the domain
in the domain 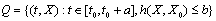 satisfy the conditions:a) for any fixed X the interval-valued mapping
satisfy the conditions:a) for any fixed X the interval-valued mapping 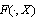 is measurable;b) for almost every fixed t the interval-valued mapping
is measurable;b) for almost every fixed t the interval-valued mapping 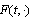 is continuous;c)
is continuous;c) 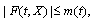 where
where 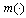 is summable on
is summable on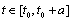 ;d)
;d) 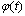 has the finite number of intervals where
has the finite number of intervals where 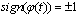 on
on 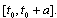 Then there exists a solution of equation (9) defined on the interval
Then there exists a solution of equation (9) defined on the interval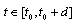 , where
, where 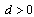 satisfies the conditionsa)
satisfies the conditionsa) 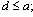 b)
b) 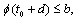 where
where 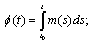 c)
c)  where
where 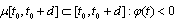 for
for 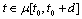 Proof. Consider the behaviour of the function
Proof. Consider the behaviour of the function 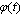 on the interval
on the interval 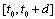 By condition d) of the theorem there exists a finite number of points
By condition d) of the theorem there exists a finite number of points 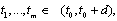
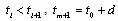 , such that the function
, such that the function 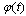 doesn’t change its sign on the interval
doesn’t change its sign on the interval 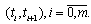 Suppose that there exists a solution of the equation (9) on the interval
Suppose that there exists a solution of the equation (9) on the interval 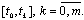 If
If 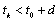 consider the equation (9) on the interval
consider the equation (9) on the interval 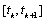 Case
Case 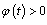 Let
Let 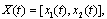
 Then the interval- valued mapping
Then the interval- valued mapping 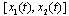 satisfies the integral equation
satisfies the integral equation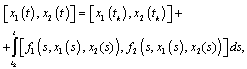 i.e. the functions
i.e. the functions 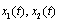 satisfy the system of integral equations
satisfy the system of integral equations Therefore the functions
Therefore the functions 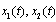 satisfy the system of differential equations
satisfy the system of differential equations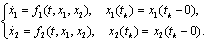 Using the Caratheodory theorem [9] we have that there exists a solution of this system defined on the interval
Using the Caratheodory theorem [9] we have that there exists a solution of this system defined on the interval 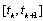 Case
Case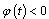 . Then the interval-valued mapping
. Then the interval-valued mapping 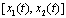 satisfies the integral equation
satisfies the integral equation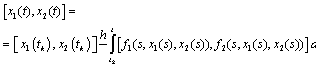 i.e. the functions
i.e. the functions 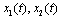 satisfy the system of integral equations
satisfy the system of integral equations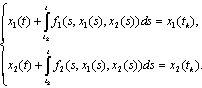 Therefore the functions
Therefore the functions 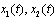 satisfy the system of differential equations
satisfy the system of differential equations 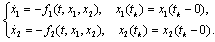 Using the Caratheodory theorem we have that there exists a solution of this system defined on the interval
Using the Caratheodory theorem we have that there exists a solution of this system defined on the interval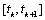 . Then there exists a solution of differential equation (9) provided that
. Then there exists a solution of differential equation (9) provided that 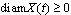 The fact that
The fact that 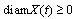 follows from the condition c) of the theorem:
follows from the condition c) of the theorem: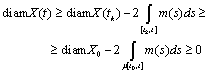 because on intervals where
because on intervals where 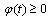
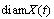 doesn't decrease. 3)
doesn't decrease. 3) 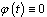 Then we have
Then we have 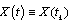 So the solution of differential equation (9) exists on
So the solution of differential equation (9) exists on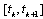 .
.4. Conclusions
- In this paper the concept of generalized differentiability (proposed in [17]) for interval-valued mappings is used. The interval-valued differential equations with generalized derivative are considered and the existence theorem is proved.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML