-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(4): 100-115
doi: 10.5923/j.am.20120204.02
Complete Classification of BKM Lie Superalgebras Possessing Strictly Imaginary Property
N. Sthanumoorthy , K. Priyadharsini
Ramanujan Institute for Advanced study in Mathematics, University of Madras, Chennai - 600 005, India
Correspondence to: N. Sthanumoorthy , Ramanujan Institute for Advanced study in Mathematics, University of Madras, Chennai - 600 005, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, complete classifications of all BKM Lie superalgebras (with finite order and infinite order Cartan matrices) possessing Strictly Imaginary Property are given. These classifications also include, in particular, the Monster BKM Lie superalgebra.
Keywords: Borcherds Kac-Moody Lie Superalgebras, Strictly Imaginary Roots, Purely Imaginary Roots
Article Outline
1. Introduction
- In[4], the theory of Lie superalgebras was given and in[5], theory of Kac- Moody Lie superalgebras was described. Borcherds[2] initiated the study of generalized Kac-Moody algebras(GKM algebras). Wakimoto[19] introduced BKM superalgebras(BKM Lie superalgebras). The existence of special imaginary roots for Kac-Moody algebras(KM algebras) were shown in[1] and the concept of special imaginary roots was extended from KM algebras to GKM algebras in[7]. In[11], some properties of roots of GKM algebras were studied and in[12],[14], special imaginary roots of these classes were found out and finally in[15], a complete classification of GKM algebras possessing special imaginary roots was found out. The notion of special imaginary roots of BKM algebras was generalized to BKM superalgebras in[16] and certain classes of BKM Lie superalgebras possessing special imaginary roots were found out in[16]. In[18], a complete classification of BKM Lie superalgebras possessing special imaginary roots was given. The concept of strictly imaginary roots for KM algebras was introduced by Kac([5],[6]). Casperson[3] gave a complete classification of KM algebras possessing strictly imaginary property. The concept of purely imaginary roots for KM algebras was introduced in[10] and therein the KM algebras possessing purely imaginary property were completely classified. Again in[13], the concept of purely imaginary roots from KM algebras to GKM was extended, and the GKM algebras possessing purely imaginary property were completely classified. In[14], the properties of strictly imaginary roots and purely imaginary roots of GKM algebras were compared and using the classification of GKM algebras possessing purely imaginary property, the algebras whose purely imaginary roots are strictly imaginary roots were found. Complete classification of GKM algebras possessing special imaginary roots and strictly imaginary property were given in[15].The concepts of strictly imaginary roots and purely imaginary roots of Borcherds Kac-Moody algebras(BKM algebras) were extended to BKM superalgebras in[17]. A complete classification of those BKM superalgebras with purely alien imaginary property and purely imaginary property were given in[17]. Moreover, the properties of strictly imaginary roots and purely imaginary roots of BKM superalgebras were compared and the BKM superalgebras whose purely imaginary roots are also strictly imaginary were found out in[17].Aim of this paper is to give a complete classification of BKM Lie superalgebras possessing strictly imaginary property.
2. Preliminaries
2.1. Basic Definitions
- In this section, we briefly recall the fundamental definitions regarding BKM Lie superalgebras, their Weyl groups and root systems as given in[19].For the definition of Generalized Generalized Cartan matrix(GGCM) one can see[9].Definition 2.1.1:[19].Let
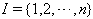 be a finite index set and let
be a finite index set and let 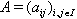 be an
be an 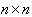 real matrix. Let
real matrix. Let 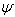 be a subset of I. If A satisfies the following conditions, then
be a subset of I. If A satisfies the following conditions, then 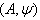 is called a BKM super matrix.
is called a BKM super matrix.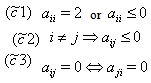
 if
if  then
then 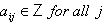
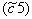 if
if 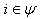 and
and 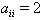 then
then 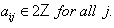 Define, subsets
Define, subsets 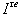 and
and 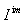 of I by
of I by 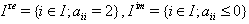 .Let
.Let 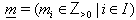 be a collection of positive integers such that
be a collection of positive integers such that 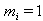 for all
for all 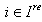 We call
We call 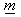 a charge of A.Also set
a charge of A.Also set 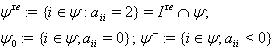 and
and 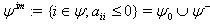 .Remarks: (1) If
.Remarks: (1) If 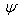 is an empty set then the BKM super matrix coincides with the corresponding BKM matrix( or GKM matrix). (2) For description of the quasi- Dynkin diagram,
is an empty set then the BKM super matrix coincides with the corresponding BKM matrix( or GKM matrix). (2) For description of the quasi- Dynkin diagram,  one can refer to[19]. A Generalized Generalized Cartan Matrix is called indecomposable if it cannot be reduced to a block diagonal form by shuffling rows and columns[8].For the sake of completeness we repeat the following fundamentals already explained in[17].Definition 2.1.2:[6] Let I be an index set.
one can refer to[19]. A Generalized Generalized Cartan Matrix is called indecomposable if it cannot be reduced to a block diagonal form by shuffling rows and columns[8].For the sake of completeness we repeat the following fundamentals already explained in[17].Definition 2.1.2:[6] Let I be an index set. 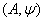 be an indecomposable BKM super matrix where
be an indecomposable BKM super matrix where 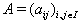 and
and 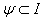 . Then one and only one of the following three possibilities holds forA.(Fin) det
. Then one and only one of the following three possibilities holds forA.(Fin) det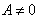 ; there exists
; there exists 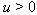 such that
such that 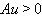 and
and 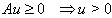 or
or 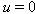 .(Aff) Corank =1; there exists
.(Aff) Corank =1; there exists 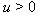 such that
such that 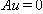 and
and 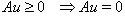 (Ind) det
(Ind) det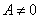 ; there exists
; there exists 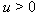 such that
such that 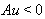 and
and 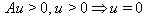 Referring to the above three cases, we say that A is of finite, affine or indefinite type respectively and write
Referring to the above three cases, we say that A is of finite, affine or indefinite type respectively and write 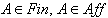 or
or 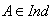 respectively.Definition 2.1.3:[18]We say that a BKM super matrix
respectively.Definition 2.1.3:[18]We say that a BKM super matrix 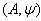 is of hyperbolic type, if it is indefinite type and every principal submatrix of A is either finite or affine type BKM super matrix.Definition 2.1.4[19]: If a BKM super matrix
is of hyperbolic type, if it is indefinite type and every principal submatrix of A is either finite or affine type BKM super matrix.Definition 2.1.4[19]: If a BKM super matrix 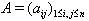 decomposes as
decomposes as 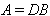 where,
where, 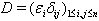 a diagonal matrix and
a diagonal matrix and 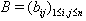 is a symmetric matrix, then A is said to be symmetrizable.If A is a symmetrizable BKM supermatrix, then taking the diagonal matrix D satisfying
is a symmetric matrix, then A is said to be symmetrizable.If A is a symmetrizable BKM supermatrix, then taking the diagonal matrix D satisfying 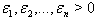 by
by 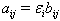 we have
we have 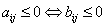 and
and 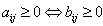 for all i and j.We assume that
for all i and j.We assume that 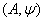 is a symmetrizable and indecomposable BKM supermatrix.Definition 2.1.5:[19] For any BKM supermatrix,
is a symmetrizable and indecomposable BKM supermatrix.Definition 2.1.5:[19] For any BKM supermatrix, 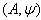 where
where 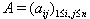 , we have a triple
, we have a triple 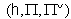 , where
, where 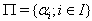 and
and 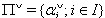 satisfying the following relations: (i)
satisfying the following relations: (i) 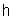 is a finite dimensional (complex) vector space such that
is a finite dimensional (complex) vector space such that 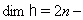 rank A. (ii)
rank A. (ii) 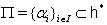 is linearly independent and
is linearly independent and 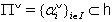 is linearly independent, where
is linearly independent, where 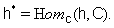 iii)
iii) 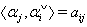 , where
, where 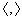 denotes a duality pairing between
denotes a duality pairing between 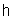 and
and 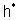 This triple
This triple 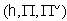 is called a realization of A.Call an element of
is called a realization of A.Call an element of 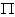 (respectively
(respectively 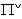 ) a fundamental root or a simple root (respectively fundamental coroot or a simple coroot).Moreover, set
) a fundamental root or a simple root (respectively fundamental coroot or a simple coroot).Moreover, set 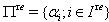 and
and 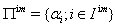 . We call an element of
. We call an element of 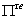 (resp.
(resp. 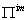 ) a real simple root (resp. an imaginary simple root).Also divide
) a real simple root (resp. an imaginary simple root).Also divide 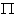 as
as 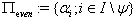 , the set of all even simple roots and
, the set of all even simple roots and 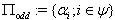 , the set of all odd simple roots. Let
, the set of all odd simple roots. Let 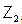 is the residue class ring mod 2 with elements
is the residue class ring mod 2 with elements 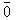 and
and 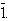 Definition 2.1.6:[19] A
Definition 2.1.6:[19] A 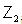 -graded vector space
-graded vector space 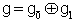 possessing the operation called the bracket product,
possessing the operation called the bracket product, 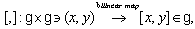 is called a Lie superalgebra if it satisfies the following conditions:
is called a Lie superalgebra if it satisfies the following conditions: 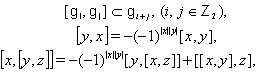 for all
for all 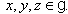 .Definition 2.1.7:[19] The Borcherds Kac-Moody Lie superalgebra (abbreviated as BKM Lie superalgebra or BKM superalgebra)
.Definition 2.1.7:[19] The Borcherds Kac-Moody Lie superalgebra (abbreviated as BKM Lie superalgebra or BKM superalgebra) 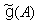 associated to a symmetrizable BKM super matrix
associated to a symmetrizable BKM super matrix 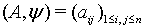 is the Lie superalgebra generated by the vector space
is the Lie superalgebra generated by the vector space 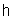 and the elements
and the elements 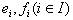 satisfying the following relations: 1.
satisfying the following relations: 1. 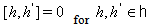 2.
2. 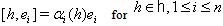 3.
3. 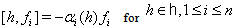 4.
4. 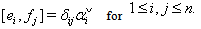 5. if
5. if 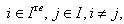 then
then 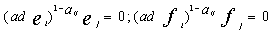 6. if
6. if 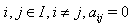 , then
, then 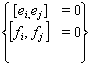 7. if
7. if 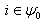 then
then 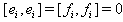 . Remarks: As we are assuming that the matrix
. Remarks: As we are assuming that the matrix 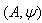 is symmetrizable, the associated BKM superalgebra
is symmetrizable, the associated BKM superalgebra  is simple (for a proof one can see[6], and also[19] ),which we will denote by
is simple (for a proof one can see[6], and also[19] ),which we will denote by 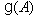 . So for a BKM supermatrix
. So for a BKM supermatrix 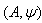 ,
, 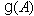 is called BKM Lie superalgebra or BKM superalgebra associated to
is called BKM Lie superalgebra or BKM superalgebra associated to 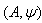 In[5], Dynkin diagrams were defined for Lie superalgebras. Dynkin diagrams were already extended from KM algebras to GKM algebras in[11] and then extended to BKM Lie superalgebras in[17], which are again given below.Definition 2.1.8:[17] To every BKM super matrix
In[5], Dynkin diagrams were defined for Lie superalgebras. Dynkin diagrams were already extended from KM algebras to GKM algebras in[11] and then extended to BKM Lie superalgebras in[17], which are again given below.Definition 2.1.8:[17] To every BKM super matrix 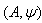 , where
, where 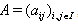 ,
, 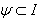 the index set I, is associated with a Dynkin diagram
the index set I, is associated with a Dynkin diagram 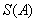 defined as follows:
defined as follows: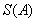 has n vertices and vertices i and j are connected by
has n vertices and vertices i and j are connected by 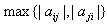 number of lines if
number of lines if 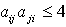 and there is an arrow pointing towards i if
and there is an arrow pointing towards i if 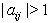 . If
. If 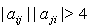 , i and j are connected by a bold faced edge equipped with the ordered pair
, i and j are connected by a bold faced edge equipped with the ordered pair 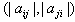 Moreover 1. if
Moreover 1. if 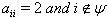 , the i-th vertex will be denoted by a white circle. 2. if
, the i-th vertex will be denoted by a white circle. 2. if 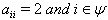 , the i-th vertex will be denoted by a white circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. 3. if
, the i-th vertex will be denoted by a white circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. 3. if 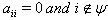 , the i -th vertex will be denoted by a crossed circle. 4. if
, the i -th vertex will be denoted by a crossed circle. 4. if 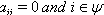 , the i -th vertex will be denoted by a crossed circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. 5. if
, the i -th vertex will be denoted by a crossed circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. 5. if 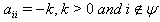 , the i -th vertex will be denoted by a white circle with
, the i -th vertex will be denoted by a white circle with 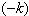 written within parentheses and above the circle. 6. if
written within parentheses and above the circle. 6. if 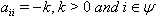 , the i -th vertex will be denoted by a white circle with
, the i -th vertex will be denoted by a white circle with 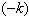 written within parentheses and above the circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. With these definitions, the Dynkin diagrams of all BKM superalgebras can be drawn.Some examples of Dynkin diagrams of BKM superalgebras were drawn in[17].A BKM Lie superalgebra
written within parentheses and above the circle with (od) written within parentheses and below the circle to denote the vertex corresponding to an odd simple root in this case. With these definitions, the Dynkin diagrams of all BKM superalgebras can be drawn.Some examples of Dynkin diagrams of BKM superalgebras were drawn in[17].A BKM Lie superalgebra 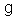 , like a KM or BKM algebra, has the following natural root space decomposition:
, like a KM or BKM algebra, has the following natural root space decomposition: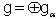 where
where 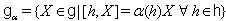 is called the root space associated to
is called the root space associated to 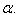 An element
An element 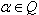 is called a root, if
is called a root, if 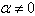 and
and 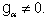 The number mult
The number mult 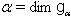 is called the multiplicity of the root α. A root α of
is called the multiplicity of the root α. A root α of 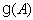 can be expressed as
can be expressed as 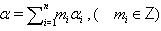 where
where 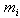 's are all
's are all 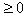 or all
or all 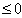 . Corresponding to whether
. Corresponding to whether 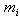 's are all
's are all 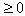 or all
or all 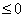 , α is called a positive root or a negative root respectively. Also
, α is called a positive root or a negative root respectively. Also 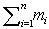 is called the height of α and is denoted by
is called the height of α and is denoted by 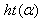 We denote by
We denote by 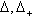 and
and 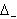 the set of all roots, positive roots and negative roots respectively. Also note that
the set of all roots, positive roots and negative roots respectively. Also note that 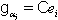 and
and 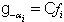 .Definition 2.1.9:[19]Let
.Definition 2.1.9:[19]Let 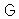 be a BKM Lie superalgebra. Set
be a BKM Lie superalgebra. Set 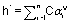 and take a subspace
and take a subspace 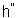 of
of 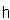 satisfying
satisfying 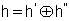 .Define the symmetric bilinear form
.Define the symmetric bilinear form 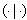 on
on 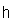 as follows:
as follows: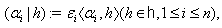
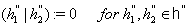 . Then
. Then 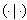 is non-degenerate on
is non-degenerate on 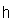 and this induces the linear isomorphism,
and this induces the linear isomorphism, 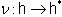 We completely identify
We completely identify 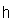 and
and 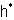 via this map v and omit the symbol v in the following results. The proofs of these results are in[19].Lemma 2.1.10:[19] For
via this map v and omit the symbol v in the following results. The proofs of these results are in[19].Lemma 2.1.10:[19] For 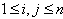 , one has the following:1.
, one has the following:1. 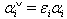 2.
2. 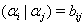 3.
3. 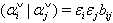 4. If
4. If 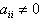 then
then 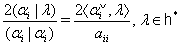 , in particular if
, in particular if 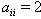 , then
, then 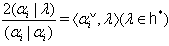 Remark: For
Remark: For 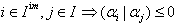 . In terms of inner product
. In terms of inner product  , we have
, we have 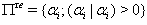 and
and 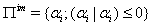 .Definition 2.1.11:[17] For each
.Definition 2.1.11:[17] For each 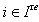 we define the simple reflection
we define the simple reflection 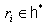 by
by 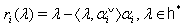 The Weyl group W of
The Weyl group W of 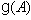 is the subgroup of
is the subgroup of 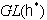 generated by the
generated by the 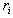 's
's 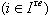 . Note that
. Note that 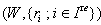 is a coxeter system. So for a real root
is a coxeter system. So for a real root 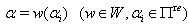 we define the reflection
we define the reflection 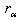 of
of 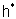 with respect to α by
with respect to α by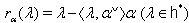 where
where 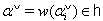 is the dual real root of
is the dual real root of 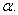 Note that
Note that 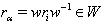 .Lemma 2.1.12:[19]. The bilinear form
.Lemma 2.1.12:[19]. The bilinear form 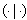 on
on 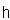 and
and 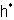 is invariant under the action of the Weyl group.In particular, we have
is invariant under the action of the Weyl group.In particular, we have 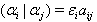 for
for 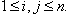 Definition 2.1.13:[17]The set of all real roots of a BKM Lie superalgebra is defined as
Definition 2.1.13:[17]The set of all real roots of a BKM Lie superalgebra is defined as 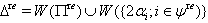 Then the set of all imaginary roots is
Then the set of all imaginary roots is 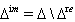 We have,
We have,  and
and 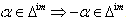 .Definition 2.1.14:[19]Let
.Definition 2.1.14:[19]Let 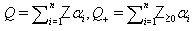 , then we have
, then we have 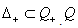 . is called the root lattice and
. is called the root lattice and 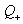 is called the positive root lattice.The root lattice
is called the positive root lattice.The root lattice 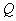 becomes a (partially) ordered set by putting
becomes a (partially) ordered set by putting 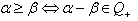 for
for 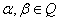 .Now, for
.Now, for 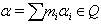 , support of α is defined as
, support of α is defined as 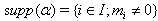 . If
. If 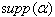 is a connected subset of the Dynkin diagram of A, we say that
is a connected subset of the Dynkin diagram of A, we say that 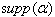 is connected.Definition 2.1.15:[19] Imaginary roots of BKM superalgebras are basically of two types, domestic-type and alien-type.Domestic-type imaginary root:An imaginary root which is conjugate to a fundamental root under the action of the Weyl group is called domestic-type imaginary root. We denote by
is connected.Definition 2.1.15:[19] Imaginary roots of BKM superalgebras are basically of two types, domestic-type and alien-type.Domestic-type imaginary root:An imaginary root which is conjugate to a fundamental root under the action of the Weyl group is called domestic-type imaginary root. We denote by 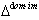 , the set of all domestic-type imaginary roots.Alien-type imaginary root:An imaginary root which is not a conjugate to a fundamental root under the action of the Weyl group is called alien-type imaginary root. We denote by
, the set of all domestic-type imaginary roots.Alien-type imaginary root:An imaginary root which is not a conjugate to a fundamental root under the action of the Weyl group is called alien-type imaginary root. We denote by 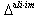 , the set of all alien-type imaginary roots.Since an imaginary root is either conjugate or not conjugate to a fundamental root under the action of Weyl group, each imaginary root is either domestic imaginary or alien imaginary.We have
, the set of all alien-type imaginary roots.Since an imaginary root is either conjugate or not conjugate to a fundamental root under the action of Weyl group, each imaginary root is either domestic imaginary or alien imaginary.We have 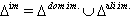 Lemma 2.1.16:[19] 1.
Lemma 2.1.16:[19] 1. 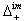 is invariant under the action of the Weyl group. 2. If
is invariant under the action of the Weyl group. 2. If 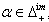 then there exists
then there exists 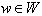 satisfying
satisfying 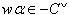 3. For
3. For 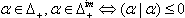 Theorem 2.1.17:[19]For a symmetrizable BKM supermatrix
Theorem 2.1.17:[19]For a symmetrizable BKM supermatrix 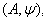 if we set
if we set 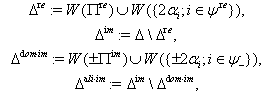 then concerning
then concerning 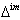 and
and 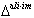 we have the following results: 1.
we have the following results: 1. 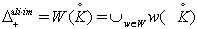 . 2.
. 2. 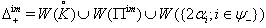 . where
. where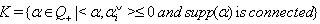 and
and 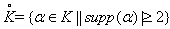 Also by notation
Also by notation 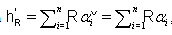
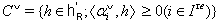 and
and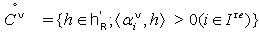 .Lemma 2.1.18:[19]For
.Lemma 2.1.18:[19]For 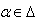 and
and 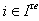 one has the following: 1. The set
one has the following: 1. The set 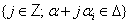 is a finite set. Let p be the minimum contained in this set, and let q be the maximum in this set. Then,
is a finite set. Let p be the minimum contained in this set, and let q be the maximum in this set. Then, 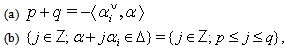 (c) the sequence
(c) the sequence 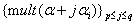 is bilaterally symmetric, and the left half of this sequence is monotone nondecreasing. Namely,1.
is bilaterally symmetric, and the left half of this sequence is monotone nondecreasing. Namely,1. 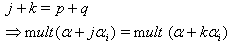
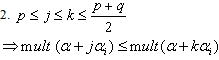
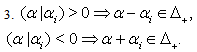
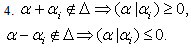 Strictly domestic type imaginary roots, strictly alien type imaginary roots, strictly imaginary roots, purely imaginary roots, purely domestic type imaginary roots and purely alien imaginary root were already explained in[17]. We repeat the following definitions which we need here.Definition 2.1.19:[`17]A domestic-type imaginary root
Strictly domestic type imaginary roots, strictly alien type imaginary roots, strictly imaginary roots, purely imaginary roots, purely domestic type imaginary roots and purely alien imaginary root were already explained in[17]. We repeat the following definitions which we need here.Definition 2.1.19:[`17]A domestic-type imaginary root 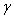 in a BKM super algebra is said to be strictly domestic-type imaginary, if for every
in a BKM super algebra is said to be strictly domestic-type imaginary, if for every 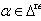 either
either 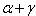 or
or 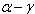 is a root. Let
is a root. Let 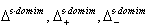 denote the set of all strictly domestic-type imaginary roots, positive and negative strictly domestic-type imaginary roots respectively.Definition 2.1.20:[17]An alien-type imaginary root
denote the set of all strictly domestic-type imaginary roots, positive and negative strictly domestic-type imaginary roots respectively.Definition 2.1.20:[17]An alien-type imaginary root 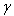 in a BKM super algebra is said to be strictly alien-type imaginary, if for every
in a BKM super algebra is said to be strictly alien-type imaginary, if for every 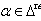 either
either 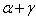 or
or 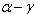 is a root. Let
is a root. Let 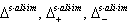 denote the set of all strictly alien-type imaginary roots, positive and negative strictly alien-type imaginary roots respectively.Definition 2.1.21:[17] An imaginary root
denote the set of all strictly alien-type imaginary roots, positive and negative strictly alien-type imaginary roots respectively.Definition 2.1.21:[17] An imaginary root 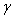 in a BKM super algebra is said to be strictly imaginary, if for every
in a BKM super algebra is said to be strictly imaginary, if for every 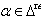 either
either 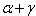 or
or 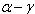 is a root. The set of all strictly imaginary roots is denoted by
is a root. The set of all strictly imaginary roots is denoted by 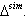 Let
Let 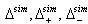 denote the set of all strictly imaginary roots, positive and negative strictly imaginary roots respectively.Remark: As it was noticed in[5],(1)If
denote the set of all strictly imaginary roots, positive and negative strictly imaginary roots respectively.Remark: As it was noticed in[5],(1)If 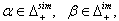 then
then 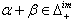 (2)
(2) 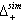 is a semigroup.Definition 2.1.22:[17] A BKM super matrix
is a semigroup.Definition 2.1.22:[17] A BKM super matrix 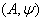 is said to have strictly imaginary property, if
is said to have strictly imaginary property, if 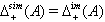 If a BKM supermatrix satisfies strictly imaginary property, we say that corresponding BKM Lie superalgebra satisfies strictly imaginary property.Purely alien imaginary roots, purely domestic imaginary roots were already explained in Sthanumoorthy et al.(2009).Definition 2.1.23:[17] Let
If a BKM supermatrix satisfies strictly imaginary property, we say that corresponding BKM Lie superalgebra satisfies strictly imaginary property.Purely alien imaginary roots, purely domestic imaginary roots were already explained in Sthanumoorthy et al.(2009).Definition 2.1.23:[17] Let 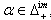 we say that α is purely imaginary, if for any
we say that α is purely imaginary, if for any 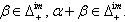 We say that the BKM super algebra
We say that the BKM super algebra 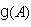 has the purely imaginary property, if
has the purely imaginary property, if 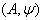 satisfies this property. We have,
satisfies this property. We have, 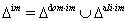 Similarly we say that a negative root
Similarly we say that a negative root 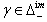 is purely imaginary if
is purely imaginary if 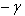 is a purely imaginary root. Denote by
is a purely imaginary root. Denote by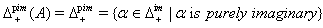 and
and 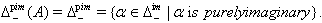 Then, the set of all purely imaginary roots is
Then, the set of all purely imaginary roots is 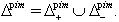 We omit the proof of the following theorem for BKM Lie superalgebras which can be directly verified using the proof for KM algebras already proved in[3].Theorem 2.1.24:[17] For BKM Lie superalgebras, the following results are true: (a) If
We omit the proof of the following theorem for BKM Lie superalgebras which can be directly verified using the proof for KM algebras already proved in[3].Theorem 2.1.24:[17] For BKM Lie superalgebras, the following results are true: (a) If 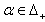 and
and 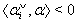 for all
for all 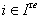 then
then 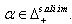 (b) If
(b) If 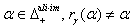 for all
for all 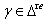 then
then 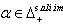 (c) If
(c) If 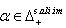 and
and 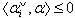 for all
for all 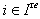 then
then 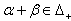 for all
for all 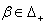 (d) If
(d) If 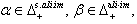 then
then 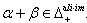 (e)
(e) 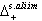 is a semigroup. In addition to the above results, we prove the following results for BKM Lie superalgebras.Theorem 2.1.25: a) If
is a semigroup. In addition to the above results, we prove the following results for BKM Lie superalgebras.Theorem 2.1.25: a) If 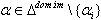 and
and 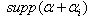 is connected, then
is connected, then 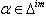 b) If
b) If 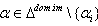
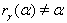 for all
for all 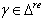 then
then 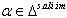 Proof: a) Let
Proof: a) Let 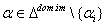 and
and 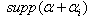 be connected. Then
be connected. Then 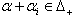 So by lemma 2.1.18.
So by lemma 2.1.18. 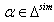 b) Let
b) Let 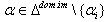 . If
. If 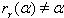 for all
for all 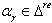 then
then 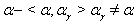
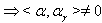
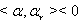 or
or 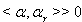 So, by lemma 2.1.18., we have
So, by lemma 2.1.18., we have 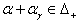 or
or 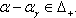 Hence α is a strictly imaginary root.Remark:From the property
Hence α is a strictly imaginary root.Remark:From the property 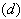 of the Theorem (2.1.24), we have
of the Theorem (2.1.24), we have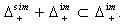
3. Complete Classification of BKM Lie Superalgebras Possessing Strictly Imaginary Property
- Remark: In[17], a complete classification of BKM Lie superalgebras possessing purely imaginary property was given.
3.1. First we Give the following Results from[3].
- Definition 3.1.1:[3] We say that the generalized Cartan matrix A has the property SIM(more briefly:
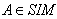 ) if
) if  Definition 3.1.2:[3]A is said to satisfy NC1, if there exists no subsets
Definition 3.1.2:[3]A is said to satisfy NC1, if there exists no subsets 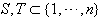 such that
such that 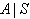 is affine or indefinite type, and
is affine or indefinite type, and 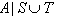 is decomposable.The following theorem proved by Casperson (1994) is for the indefinite Kac-Moody algebras possessing strictly imaginary property. Casperson (1994) gave a complete classification of Kac-Moody algebras possessing strictly imaginary property.Theorem 3.1.3:[3] A GCM lies in SIM if and only if it satisfies the condition NC1 and has no principal submatrix contained in the following list:1. The
is decomposable.The following theorem proved by Casperson (1994) is for the indefinite Kac-Moody algebras possessing strictly imaginary property. Casperson (1994) gave a complete classification of Kac-Moody algebras possessing strictly imaginary property.Theorem 3.1.3:[3] A GCM lies in SIM if and only if it satisfies the condition NC1 and has no principal submatrix contained in the following list:1. The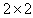 matrices of the form
matrices of the form 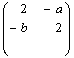 with
with 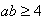 and
and 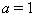 or
or 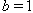 2. The matrices of the following Dynkin diagrams of twisted affine type:
2. The matrices of the following Dynkin diagrams of twisted affine type: 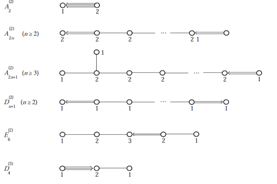 3. The strictly hyperbolic
3. The strictly hyperbolic 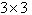 matrices associated with the Dynkin diagrams of the form:
matrices associated with the Dynkin diagrams of the form: 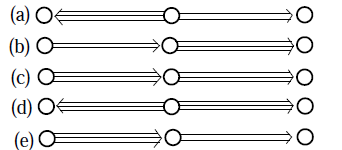 4. The hyperbolic
4. The hyperbolic 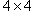 matrices associated with the Dynkin diagrams of the form:
matrices associated with the Dynkin diagrams of the form: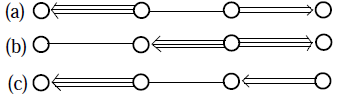 From[3], we can conclude the following for affine Kac-Moody algebras:5. If an algebra is affine, we have that
From[3], we can conclude the following for affine Kac-Moody algebras:5. If an algebra is affine, we have that 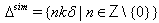 and hence
and hence 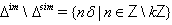 where
where 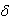 is the unique minimal positive imaginary root and k is the order of the diagram automorphism used to construct the algebra.Again for the case of
is the unique minimal positive imaginary root and k is the order of the diagram automorphism used to construct the algebra.Again for the case of 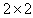 matrices, the following theorem gives a complete classification of the non-strictly imaginary roots:Theorem 3.1.4:[3]Suppose, for the GCM
matrices, the following theorem gives a complete classification of the non-strictly imaginary roots:Theorem 3.1.4:[3]Suppose, for the GCM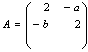 ,
, 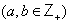 , that
, that 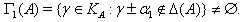 Then, either 1.
Then, either 1. 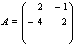 and
and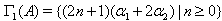 (or) 2.
(or) 2. 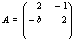 where
where 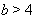 and
and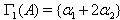 Corollary 3.1.5:[3]The GCM
Corollary 3.1.5:[3]The GCM 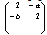 is not in SIM if and only if
is not in SIM if and only if 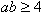 and either
and either 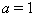 or
or 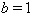 Proposition 3.1.6:[3] A GCM of affine type is a member of SIM if and only if it is of non-twisted affine type. Remarks:From[17], the set of all strictly imaginary roots of any BKM superalgebra is a subset of set of all purely imaginary roots, that is ,
Proposition 3.1.6:[3] A GCM of affine type is a member of SIM if and only if it is of non-twisted affine type. Remarks:From[17], the set of all strictly imaginary roots of any BKM superalgebra is a subset of set of all purely imaginary roots, that is , 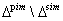 may be an empty set or non-empty set depending upon the algebras. So, for the BKM superalgebras possessing purely imaginary property, we verify whether the set
may be an empty set or non-empty set depending upon the algebras. So, for the BKM superalgebras possessing purely imaginary property, we verify whether the set 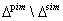 is empty or not. In the case where
is empty or not. In the case where 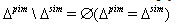 all purely imaginary roots are strictly imaginary as
all purely imaginary roots are strictly imaginary as 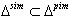 is always true. BKM superalgebras which satisfy the condition
is always true. BKM superalgebras which satisfy the condition 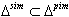 will be in the class of BKM algebras possessing strictly imaginary property.Hence the condition
will be in the class of BKM algebras possessing strictly imaginary property.Hence the condition 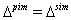 is equivalent to
is equivalent to 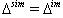 which is equivalent to SIM property.
which is equivalent to SIM property.3.2. As in the Cases of Special And Purely Imaginary Roots We Divide The Classes of BKM Superalgebras Into Two Categories. We Divide these BKM Lie Superalgebras into Two Categories.
- Category 1: BKM Lie superalgebras without odd roots(GKM algebras only)Category 2: BKM Lie superalgebras with a non-empty set of odd roots:We discuss category 1 below.Category 1: BKM Lie superalgebras without odd root:(GKM algebras only) Complete classification of GKM algebras possessing Strictly imaginary property was already given in[17].Category 2: BKM Lie superalgebras with a non-empty set of odd roots:We divide this category 2 into two classes, which are Category2: Class(I): BKM Lie superalgebras of finite order Cartan matrices and with a non-empty set of odd roots Category2: Class(II): BKM Lie superalgebras of infinite order Cartan matrices and with a non-empty set of odd roots We discuss below these two classes separately .Category 2:Class(I): BKM Lie superalgebras with a non-empty set of odd rootsWe classify these BKM superalgebras into three subclasses (i),(ii) and (iii).(i).BKM superalgebras with all simple roots being real with a non-empty set of odd roots: These are BKM superalgebras which do not have any imaginary root. So this set of BKM superalgebras do not possess strictly imaginary property.(ii).BKM superalgebras all whose simple roots are imaginary with a non-empty set of odd roots:These are BKM superalgebras whose supermatrices do not appear as the extensions of KM matrices. So all the diagonal elements are negative. Hence there is no real simple root and all the roots are imaginary and also strictly imaginary.(iii).BKM superalgebras with finite (non-zero) number of real simple roots and finite (non-zero) number of imaginary simple roots with a non-empty set of odd roots:Remark: Hereafter we denote by GGX, a Generalized Generalized Cartan matrix ( BKM super matrix or BKM matrix). We prove the following theorem for this case.Theorem 3.2.1: Let
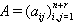 (the symmetrizable GGX)
(the symmetrizable GGX) Here
Here 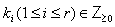
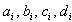 are positive integers . Moreover, GX is KM matrix of finite, affine or indefinite type of order
are positive integers . Moreover, GX is KM matrix of finite, affine or indefinite type of order 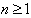 and GGX is a supermatrix of finite, affine or indefinite type with r simple imaginary roots added to that of GX. Then the following results are true for BKM superalgebras with odd roots. 1. GX is of finite type: (a) If
and GGX is a supermatrix of finite, affine or indefinite type with r simple imaginary roots added to that of GX. Then the following results are true for BKM superalgebras with odd roots. 1. GX is of finite type: (a) If 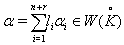 with
with 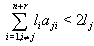 (for all
(for all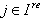 ) is true for all
) is true for all 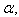 then the corresponding BKM superalgebra satisfies SIM property.(b)If
then the corresponding BKM superalgebra satisfies SIM property.(b)If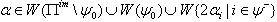
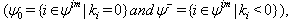 with
with 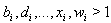 in the above GGX for
in the above GGX for 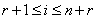 is true for all
is true for all 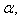 then the corresponding BKM superalgebra satisfies SIM property. Here in (a) and (b),
then the corresponding BKM superalgebra satisfies SIM property. Here in (a) and (b), 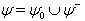 is the set of all odd roots and
is the set of all odd roots and 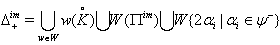 is the set of all positive imaginary roots. 2. GX is of untwisted affine type: (a) If
is the set of all positive imaginary roots. 2. GX is of untwisted affine type: (a) If 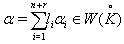 with
with 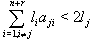 (for all
(for all 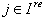 ) is true for all
) is true for all 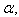 then the corresponding BKM Lie superalgebra satisfies SIM property.(b)If
then the corresponding BKM Lie superalgebra satisfies SIM property.(b)If 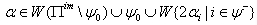 with
with 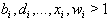 in the above GGX for
in the above GGX for 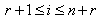 is true for all
is true for all 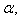 then the corresponding BKM Lie superalgebra satisfies SIM property. 3. If GX is of twisted affine type, then Strictly imaginary property does not hold. 4. If GX is of indefinite type, then Strictly imaginary property does not always hold.Proof:In the usual notation, let
then the corresponding BKM Lie superalgebra satisfies SIM property. 3. If GX is of twisted affine type, then Strictly imaginary property does not hold. 4. If GX is of indefinite type, then Strictly imaginary property does not always hold.Proof:In the usual notation, let 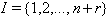 with
with 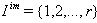 and
and 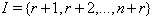
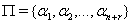 is the set of all simple roots with
is the set of all simple roots with 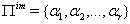 is the set of all simple imaginary roots and
is the set of all simple imaginary roots and 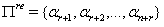 is the set of all simple real roots. Ingeneral
is the set of all simple real roots. Ingeneral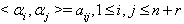 and
and 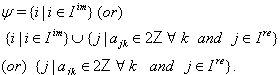 (1) Let GX be of finite type GCM and
(1) Let GX be of finite type GCM and 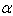 be an positive imaginary root. Then
be an positive imaginary root. Then 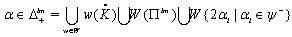 Here
Here 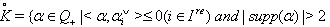 We discuss below Case(a), Case(b) and Case(c) separately. Case(a): If
We discuss below Case(a), Case(b) and Case(c) separately. Case(a): If 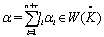 then we have
then we have 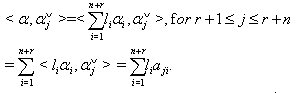 By Theorem 2.1.24.(a), it is clear that if
By Theorem 2.1.24.(a), it is clear that if 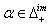 and
and 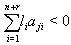 then Strictly imaginary property holds.Case(b): If
then Strictly imaginary property holds.Case(b): If 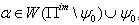 then
then 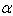 can be written as
can be written as 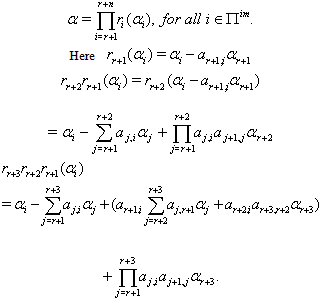 Finally,
Finally, 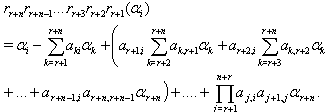 We divide this case(b) into Case(b)(1), Case(b)(2) (Case(b)(2)(i),Case(b)(2)(ii)) and Case(b)(3) separately.Case(b)(1): Let
We divide this case(b) into Case(b)(1), Case(b)(2) (Case(b)(2)(i),Case(b)(2)(ii)) and Case(b)(3) separately.Case(b)(1): Let 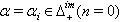 We have
We have 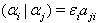 for
for 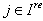 Since
Since 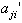 s are always negative integers and
s are always negative integers and 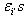 are always positive, by theorem 2.1.25., it is clear that
are always positive, by theorem 2.1.25., it is clear that 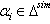 Case(b)(2):Let
Case(b)(2):Let 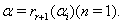 Case(b)(2)(i): Let
Case(b)(2)(i): Let 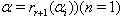 with
with 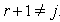 If
If 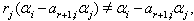 by the theorem 2.1.25,
by the theorem 2.1.25, 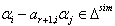 On the contrary, if
On the contrary, if 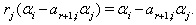 Then
Then 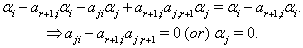 As
As 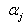 is a real simple root,
is a real simple root, 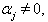
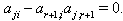 This is also not true, because
This is also not true, because 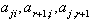 are negative integers. So by theorem 2.1.25.,
are negative integers. So by theorem 2.1.25., 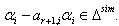 Case(b)(2)(ii): Let
Case(b)(2)(ii): Let 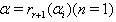 with
with 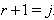 Then
Then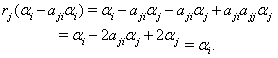 But
But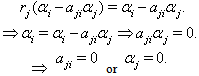 Here
Here 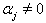 because
because 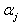 is a simple real root and
is a simple real root and 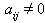 for
for 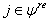 with
with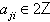 and
and 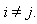 So
So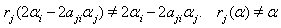 with
with 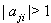 Hence by theorem 2.1.25.,
Hence by theorem 2.1.25., 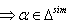 if
if 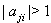 Case(b)(3):Let
Case(b)(3):Let 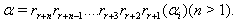 We have
We have 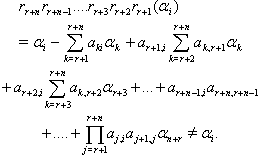 As all the
As all the 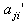 s are negative integers , by theorem 2.1.25.,
s are negative integers , by theorem 2.1.25., 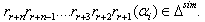 Case(c): If
Case(c): If 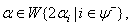 then can be written as
then can be written as 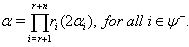 Here
Here 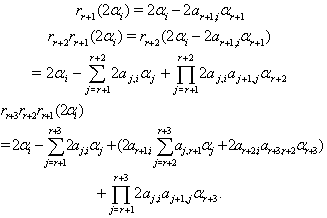 Finally,
Finally, 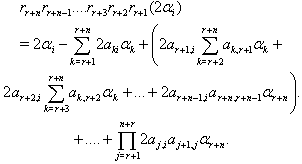 We discuss below Case(c)(1), Case(c)(2) and Case(3) separately in Case(c).Case(c)(1): Let
We discuss below Case(c)(1), Case(c)(2) and Case(3) separately in Case(c).Case(c)(1): Let 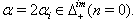 We have
We have 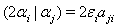 for
for 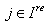 Since
Since 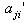 s are always negative integers and
s are always negative integers and 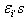 are always positive, by theorem 2.1.25., it is clear that
are always positive, by theorem 2.1.25., it is clear that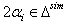 Case(c)(2): Let
Case(c)(2): Let 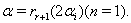 Case(c)(2)(i):Let
Case(c)(2)(i):Let 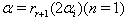 with
with 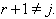 If
If 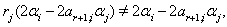 then
then 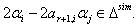 We have,
We have, 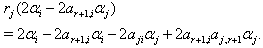 But
But 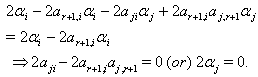 As
As 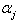 is a real simple root with
is a real simple root with 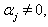
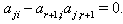 This is not true, because
This is not true, because 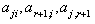 are negative integers. So by theorem 2.1.25.,
are negative integers. So by theorem 2.1.25., 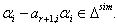 Case(c)(2)(ii): Let
Case(c)(2)(ii): Let 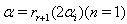 with
with 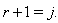 Then
Then 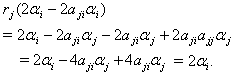 But
But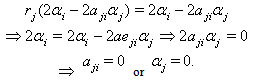 Here
Here 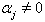 because
because 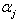 is a simple real root and
is a simple real root and 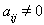 for
for 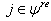 with
with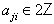 and
and 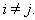 So
So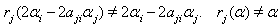 with
with  By theorem 2.1.25.,
By theorem 2.1.25., 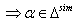 if
if 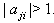 Case(c)(3):Let
Case(c)(3):Let 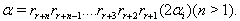 We have
We have 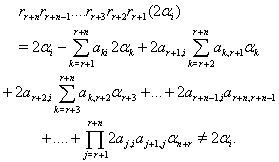 As all the
As all the 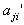 s are negative integers, by theorem 2.1.25.,
s are negative integers, by theorem 2.1.25., 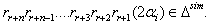 (2) Let GX be of untwisted affine type. For KM algebras of untwisted affine type, SIM property holds as per Casperson(1994). For BKM algebras with odd roots which we get as extensions of KM algebras untwisted affine type, the proof is exactly same to case(1) and hence SIM property holds.(3) Let GX be of twisted affine type. As per Casperson(1994) mentioned above, SIM property does not hold for KM algebras and the same is true for BKM Lie superalgebras which appear as extension of KM algebras of twisted affine type. Hence SIM property does not hold.(4)Let GX be of indefinite type. As far as indefinite BKM Lie superalgebras are concerned, extension of finite and untwisted affine type of KM algebras will hold SIM property, where as other algebras do not hold. The following example will illustrate the above theorem.Example: Extension of finite type Let
(2) Let GX be of untwisted affine type. For KM algebras of untwisted affine type, SIM property holds as per Casperson(1994). For BKM algebras with odd roots which we get as extensions of KM algebras untwisted affine type, the proof is exactly same to case(1) and hence SIM property holds.(3) Let GX be of twisted affine type. As per Casperson(1994) mentioned above, SIM property does not hold for KM algebras and the same is true for BKM Lie superalgebras which appear as extension of KM algebras of twisted affine type. Hence SIM property does not hold.(4)Let GX be of indefinite type. As far as indefinite BKM Lie superalgebras are concerned, extension of finite and untwisted affine type of KM algebras will hold SIM property, where as other algebras do not hold. The following example will illustrate the above theorem.Example: Extension of finite type Let 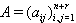 ( the symmetrizable GGX)
( the symmetrizable GGX) 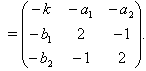 This is a BKM supermatrix of indefinite type denoted by
This is a BKM supermatrix of indefinite type denoted by 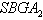 , which is an extension of finite type
, which is an extension of finite type 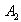 .If
.If 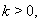
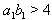 and
and 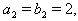 then the Dynkin diagram can be drawn as follows:
then the Dynkin diagram can be drawn as follows: 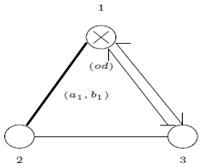 | Figure 1. Dynkin diagram of SBGA2 |
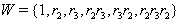 .
.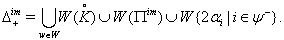 Here
Here 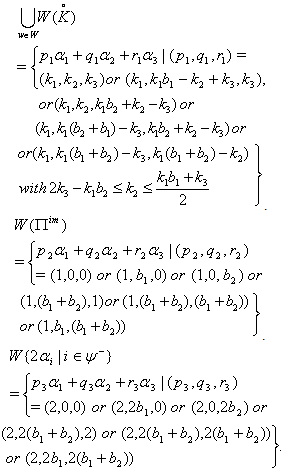 Case(a):
Case(a): 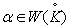 . The following relations (i), (ii),...,(vii) can be directly verified.(i)If
. The following relations (i), (ii),...,(vii) can be directly verified.(i)If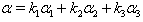 with
with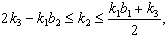 then
then 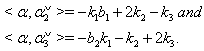 (ii) If
(ii) If 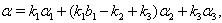 with
with 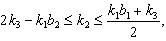 then
then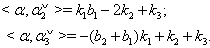 (iii) If
(iii) If 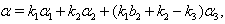 with
with 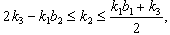 then
then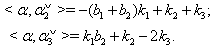 (iv)If
(iv)If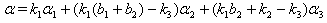 with
with 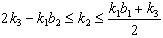 then
then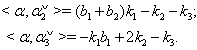 (v)If
(v)If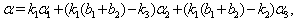 with
with 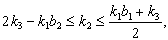 then
then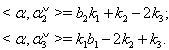 (vi)If
(vi)If 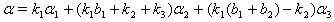 with
with 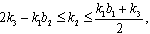 then
then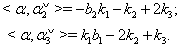 By Theorem 2.1.24., and from the above results (i), (ii), (iii), (iv), (v) and (vi), it is clear that if
By Theorem 2.1.24., and from the above results (i), (ii), (iii), (iv), (v) and (vi), it is clear that if 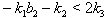 and
and 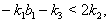 that is if (in general),
that is if (in general), 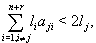 then
then 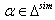 for all
for all 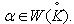 Case (b): Let
Case (b): Let 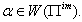 The following relations (i), (ii),...,(vi) can be easily verified. (i)If
The following relations (i), (ii),...,(vi) can be easily verified. (i)If 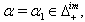 we get
we get 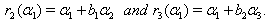 By Theorem 2.1.25., if
By Theorem 2.1.25., if 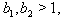 then
then 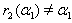 and
and 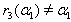 which implies
which implies 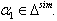 (ii) If
(ii) If 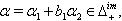 we get
we get 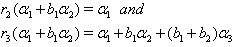 (iii) If
(iii) If 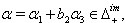 we get
we get 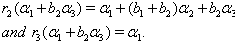 (iv) If
(iv) If 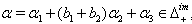 we get
we get 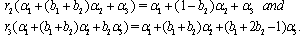 (v) If
(v) If 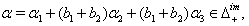 we get
we get 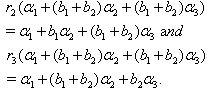 (vi) If
(vi) If 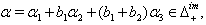 we get
we get 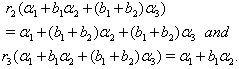 From the above results (ii), (iii), (iv), (v) and (vi) with
From the above results (ii), (iii), (iv), (v) and (vi) with 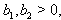 it is clear that
it is clear that 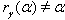 for
for 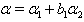 in (ii),
in (ii), 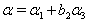 in (iii),
in (iii), 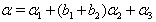 in (iv),
in (iv), 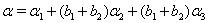 in (v),
in (v), 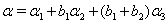 in (vi). Hence, by Theorem 2.1.25., SIM property holds.In general, if
in (vi). Hence, by Theorem 2.1.25., SIM property holds.In general, if 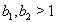 then
then 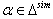 for
for 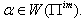 Case(c): Let
Case(c): Let 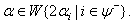 The following relations (i),(ii),...,(vi) can be directly verified.(i)If
The following relations (i),(ii),...,(vi) can be directly verified.(i)If 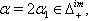 we get
we get 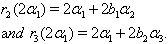 By Theorem 2.1.25., if
By Theorem 2.1.25., if 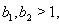 then
then 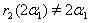 and
and 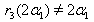 which implies
which implies 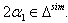 (ii) If
(ii) If 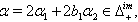 we get
we get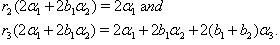 (iii) If
(iii) If 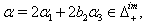 we get
we get 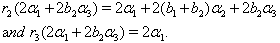 (iv) If
(iv) If 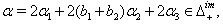 we get
we get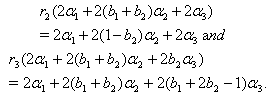 (v)If
(v)If 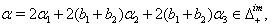 we get
we get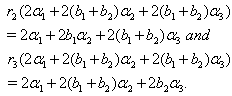 (vi) If
(vi) If 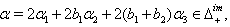 we get
we get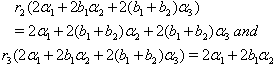 From the above results (ii), (iii), (iv), (v) and (vi) with
From the above results (ii), (iii), (iv), (v) and (vi) with 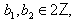 it is clear that
it is clear that 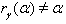 for
for 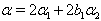 in (ii),
in (ii), 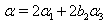 in (iii),
in (iii), 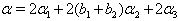 in (iv),
in (iv), 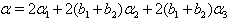 in (v),
in (v), 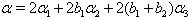 in (vi). Hence, by theorem 2.1.25., SIM property holds. In general, for
in (vi). Hence, by theorem 2.1.25., SIM property holds. In general, for 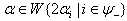 SIM property holds if
SIM property holds if 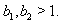 Example: Extension of untwisted affine type Let
Example: Extension of untwisted affine type Let 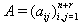 (the symmetrizable GGX)
(the symmetrizable GGX) 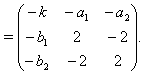 This is a BKM supermatrix of indefinite type denoted by
This is a BKM supermatrix of indefinite type denoted by 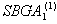 , which is an extension of untwisted affine type
, which is an extension of untwisted affine type 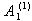 . If k=0,
. If k=0, 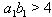 and
and 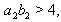 then the Dynkin diagram can be drawn as follows:
then the Dynkin diagram can be drawn as follows: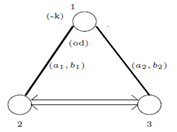 | Figure 2. Dynkin diagram of SBGA1(1). |
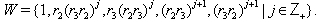 Then
Then 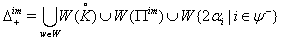 Here
Here  Case(a):Let
Case(a):Let 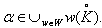 The following relations (i),(ii), ....,(vi) can be easily verified.(i) If
The following relations (i),(ii), ....,(vi) can be easily verified.(i) If 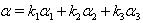 with
with 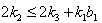 and
and 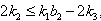 then
then 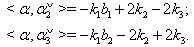 (ii) If
(ii) If 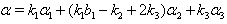 with
with 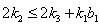 and
and 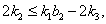 then
then 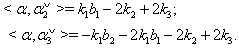 (iii) If
(iii) If 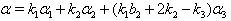 with
with 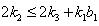 and
and 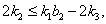 then
then 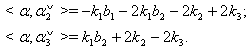 (iv) If
(iv) If 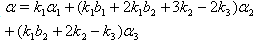 with
with 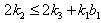 and
and 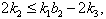 then
then 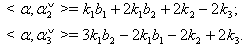 (v) If
(v) If  with
with 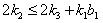 and
and 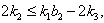 then
then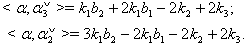 (vi)If
(vi)If 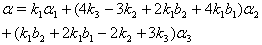 with
with 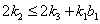 and
and 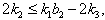 then
then 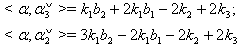 Similarly, we can find
Similarly, we can find 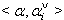 for different
for different 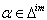 and
and 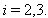 Hence by Theorem 2.1.24., and by the above results (i),(ii), ....,(vi) and others, it is clear that
Hence by Theorem 2.1.24., and by the above results (i),(ii), ....,(vi) and others, it is clear that 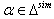 for all
for all 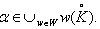 if
if 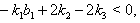
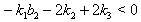 and
and 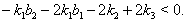 That is if
That is if 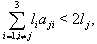 SIM property holds.Case(b): Let
SIM property holds.Case(b): Let 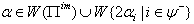 The following relations (i), (ii),...,(iv) can be easily verified.(i)If
The following relations (i), (ii),...,(iv) can be easily verified.(i)If 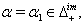 we get
we get 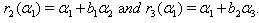 By Theorem 2.1.25., if
By Theorem 2.1.25., if 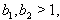 then
then 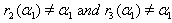 which implies
which implies 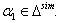 (ii) If
(ii) If 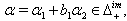 we get
we get 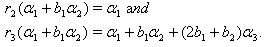 (iii) If
(iii) If 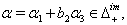 we get
we get 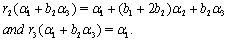 we get
we get 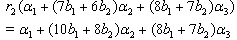
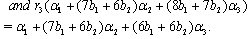 Similarly, we can find
Similarly, we can find  for
for  and
and  Hence by Theorem 2.1.25., and by the above results (ii), (iii) and others, with
Hence by Theorem 2.1.25., and by the above results (ii), (iii) and others, with 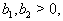 it is clear that
it is clear that 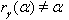 for
for 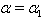 ,
,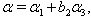
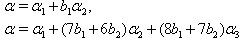 ,.....
,..... 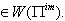 In general, if
In general, if 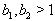 we get
we get 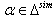 for
for 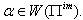 Case(C): If
Case(C): If 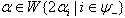 The following relations (i), (ii),...,(iv) can be easily verified.(i)If
The following relations (i), (ii),...,(iv) can be easily verified.(i)If 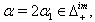 we get
we get 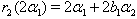 and
and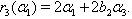 By Theorem 2.1.25., if
By Theorem 2.1.25., if 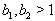 then
then 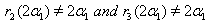 which implies
which implies 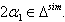 (ii) If
(ii) If 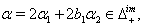 we get
we get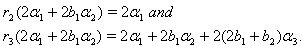 (iii) If
(iii) If 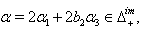 we get
we get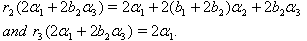 (iv)If
(iv)If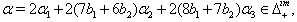 we get
we get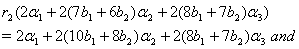
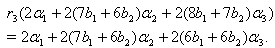 Similarly, we can find
Similarly, we can find 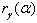 for
for 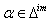 and
and 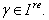 Hence by Theorem 2.1.25 and by the above results (ii), (iii),...,(iv) and others, with
Hence by Theorem 2.1.25 and by the above results (ii), (iii),...,(iv) and others, with 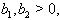 it is clear that
it is clear that 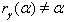 for
for 
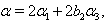
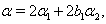 .....,
.....,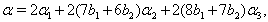 .....
.....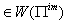 In general, if
In general, if 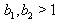 we get
we get 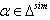 for
for 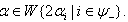 Class(II): BKM Lie superalgebras of infinite order and with a finite non-empty set of odd roots We divide this class into three subclasses.(i) All simple roots are imaginary(odd or even)(ii) One simple real root(odd or even) and infinite number of imaginary roots(odd or even) (iii) Finite number of simple real roots and infinite number of imaginary roots.We discuss these cases below(i) All simple roots are imaginary(odd or even): For this class, all the roots are imaginary. So these algebras satisfy strictly imaginary property.(ii) One simple real root(odd or even) and infinite number of imaginary roots(odd or even): We prove the following theorem for this case. Theorem 3.2.2: Let
Class(II): BKM Lie superalgebras of infinite order and with a finite non-empty set of odd roots We divide this class into three subclasses.(i) All simple roots are imaginary(odd or even)(ii) One simple real root(odd or even) and infinite number of imaginary roots(odd or even) (iii) Finite number of simple real roots and infinite number of imaginary roots.We discuss these cases below(i) All simple roots are imaginary(odd or even): For this class, all the roots are imaginary. So these algebras satisfy strictly imaginary property.(ii) One simple real root(odd or even) and infinite number of imaginary roots(odd or even): We prove the following theorem for this case. Theorem 3.2.2: Let 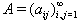 (the symmetrizable GGX)
(the symmetrizable GGX)  Here
Here 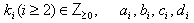 are positive integers and GGX is the BKM supermatrix with one real simple root and infinite number of imaginary roots. If
are positive integers and GGX is the BKM supermatrix with one real simple root and infinite number of imaginary roots. If 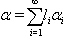 with
with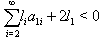 is true for all
is true for all 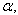 then the corresponding BKM Lie superalgebra satisfies Strictly imaginary property.Proof:In the usual notation
then the corresponding BKM Lie superalgebra satisfies Strictly imaginary property.Proof:In the usual notation 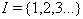 with
with 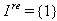 and
and 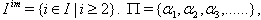 with
with 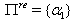 and
and 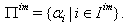 We define
We define 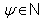 and
and 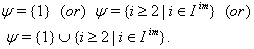 Let
Let 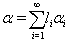 and
and 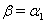 . Then by Theorem 2.1.24.,
. Then by Theorem 2.1.24., 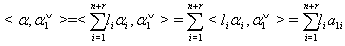 If
If 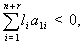 which is same as
which is same as 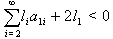 then Strictly imaginary property holds.Remark: For BKM superalgebras which appear as extension of twisted affine type(Case 3) and extension of indefinite type(Case 4), examples were given in[17](
then Strictly imaginary property holds.Remark: For BKM superalgebras which appear as extension of twisted affine type(Case 3) and extension of indefinite type(Case 4), examples were given in[17]( 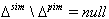 set)(Section 4, Case 3, subcase 2).Remarks:We have seen above that in the case of BKM Lie superalgebras of infinite order with one simple real root (odd or even ) and infinite number of imaginary roots (odd or even) for
set)(Section 4, Case 3, subcase 2).Remarks:We have seen above that in the case of BKM Lie superalgebras of infinite order with one simple real root (odd or even ) and infinite number of imaginary roots (odd or even) for 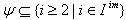 SIM property holds only when
SIM property holds only when 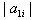 and
and 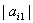 are all greater than one. As a counter example, we consider Monster Lie superalgebra with one simple real root and infinite number of simple imaginary roots(odd or even). Consider
are all greater than one. As a counter example, we consider Monster Lie superalgebra with one simple real root and infinite number of simple imaginary roots(odd or even). Consider 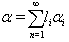 with
with 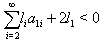 and
and 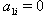 for
for 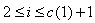 (c(1): multiplicity of the root corresponding to -2 ). As
(c(1): multiplicity of the root corresponding to -2 ). As 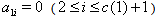 , the corresponding BKM Lie superalgebra does not satisfy SIM property. We prove this below. Consider Monster Lie superalgebra which has the following supermatrix as defined below: Let
, the corresponding BKM Lie superalgebra does not satisfy SIM property. We prove this below. Consider Monster Lie superalgebra which has the following supermatrix as defined below: Let 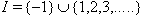 be an index set and consider the Borcherds-Cartan super matrix
be an index set and consider the Borcherds-Cartan super matrix 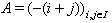 with charge
with charge 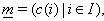 where
where 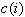 are the coefficients of the elliptic modular function
are the coefficients of the elliptic modular function 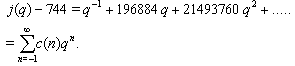 Here
Here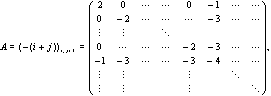 is the BKM supermatrix and
is the BKM supermatrix and 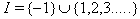 We define
We define 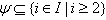
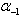 is the real root corresponding to the diagonal element 2 and
is the real root corresponding to the diagonal element 2 and 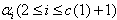 are the imaginary roots corresponding to the diagonal element -2 We consider any
are the imaginary roots corresponding to the diagonal element -2 We consider any 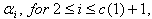 then
then 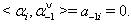 This implies
This implies 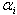 does not satisfy the strictly imaginary property for
does not satisfy the strictly imaginary property for 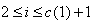 . Hence Strictly imaginary property does not hold for a Monster Lie superalgebra.(iii) Finite number(atleast two) of simple real roots and infinite number of imaginary roots: We prove the following theorem for this case. Theorem 3.2.3: Let
. Hence Strictly imaginary property does not hold for a Monster Lie superalgebra.(iii) Finite number(atleast two) of simple real roots and infinite number of imaginary roots: We prove the following theorem for this case. Theorem 3.2.3: Let 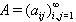 ( the symmetrizable GGX)
( the symmetrizable GGX)  Here
Here 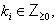
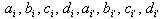 are positive integers and GGX is the BKM supermatrix with
are positive integers and GGX is the BKM supermatrix with 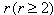 real simple roots and infinite number of imaginary roots. If
real simple roots and infinite number of imaginary roots. If 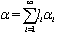 with
with 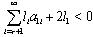 is true for all
is true for all 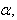 then the corresponding BKM Lie superalgebra satisfies Strictly imaginary property. Proof:In the usual notations
then the corresponding BKM Lie superalgebra satisfies Strictly imaginary property. Proof:In the usual notations 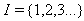 with
with 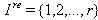 (
(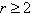 ) and
) and 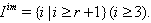 Here,
Here, 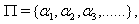 the set of all simple roots with
the set of all simple roots with 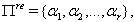 the set of simple real root and
the set of simple real root and 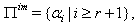 the set of all simple imaginary roots. We define
the set of all simple imaginary roots. We define 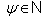 and
and 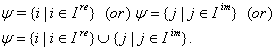 Let
Let 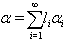 and
and 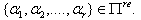
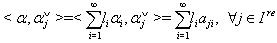 As all
As all 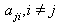 are negative integers and
are negative integers and 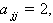 we have
we have 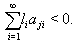 Hence
Hence 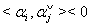 and SIM property holds.Remarks: As in the case of Monster Lie superalgebra with one simple real root and infinite number of imaginary simple roots with the condition
and SIM property holds.Remarks: As in the case of Monster Lie superalgebra with one simple real root and infinite number of imaginary simple roots with the condition 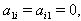 we can consider BKM Lie superalgebras with two simple real roots and infinite number of imaginary simple roots with the condition,
we can consider BKM Lie superalgebras with two simple real roots and infinite number of imaginary simple roots with the condition, 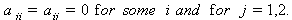 In this case, as
In this case, as 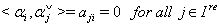 and for some
and for some 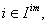 (similar to Monster Lie superalgebra as in theorem 3.2.3. ) SIM property does not hold . Hence we understand that for the infinite order case, the SIM property depends on the non-diagonal non-zero entries of the corresponding BKM supermatrix.
(similar to Monster Lie superalgebra as in theorem 3.2.3. ) SIM property does not hold . Hence we understand that for the infinite order case, the SIM property depends on the non-diagonal non-zero entries of the corresponding BKM supermatrix. 4. Conclusions
- In this paper, a complete classification of Borcherds Kac-Moody Lie superalgebras possessing strictly imaginary property is given. From this classification, one can understand that strictly imaginary property depends mainly on the coefficients of the corresponding BKM supermatrix. With these findings, different complete classifications of Borcherds Kac-Moody Lie superalgebras possessing special imaginary roots, purely imaginary roots and strictly imaginary roots were separately found out in different research papers. In fact, these classifications will be very much helpful to the researchers to extend these classes of root systems to other types of finite and infinite dimensional Lie (super)algebras. Moreover, other characteristics of these classes of Borcherds Kac-Moody Lie superalgebras possessing these root systems can also be studied. These findings may also lead to many other applications.
ACKNOWLEDGEMENTS
- The research has been financially supported by the University Grants Commission (UGC), Govt. of India, through the Major research Project, F.No.36-272/2008(SR). The authors, N.Sthanumoorthy (Principal Investigator of the Project) and K.Priyadharsini(Project Fellow for the Project) are thankful to the UGC for the same.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML -function, classical Mobius function and the very strange formula, Adv. Math, vol 30, pp 85-136, 1978.
-function, classical Mobius function and the very strange formula, Adv. Math, vol 30, pp 85-136, 1978.