Deepti Seth
Department of Mathematics,Raj Kumar Goel Engineering College, Ghaziabad. India
Correspondence to: Deepti Seth , Department of Mathematics,Raj Kumar Goel Engineering College, Ghaziabad. India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A simple mathematical model for the steady state oxygen distribution in the eye has been developed. The model introduces the krogh retinal cylinder surrounded by retinal capillary.The analytical solution to the governing equations are obtained in normalized forms by employing perturbation techniques for the arterial end ,the central region and the venous end of the retinal cylinder. Solutions are obtained for each of these regions. The computational results are presented through the graphs. The effect of important parameters on the retinal capillary concentration , are examined and discussed. The results of the model may contribute when axial diffusion is important and when it can be neglected.
Keywords:
Retinal Capillary, Oxygen Transport, Retinal Tissue
1. Introduction
Oxygen is essential for the metabolism of retinal cells and thus for their functioning. Retinal tissue is considered metabolically as a very active tissue and is sensitive to hypoxic conditions.Even in health the functional serve of oxygen in the human retina lasts for only seconds. The function of the blood is transportation of nutrients and oxygen to the tissue will be comprised two separate vascular system: the retinal vascularization and the choroidal vascularizatio. The former one supplies the inner two-thirds of the retina[3,4]through three layers of capillary networks including the radial peripapillary capillaries and a superficial and deep layer of capillaries. The retinal circulation shows progressive slowing of linear flow rate in arterioles and capillaries. Therefore, retinal circulation is characterized by a low blood flow and a high level of oxygen extraction; arteriovenous difference in partial pressure of oxygen (pO2) is about 40% . To ensure a selective exchange of substances between the blood and the surrounding tissues, retinal vascular endothelial cells[5,6] are non-fenestrated, tightly joined, and form an inner blood-retinal barrier between the retinal capillaries and the tissue . Thus, retinal capillaries, [7,8] classified as continuous capillaries, are a tube developed by the endothelial cells with no intercellular or intracellular gaps or small intercellular gaps. Gases such as O2 and CO2 can transport across the capillary walls.The transport of oxygen from the lungs to the systematic capillaries is accomplished by a process of bulk flow as oxygenated blood is carried to the tissues. Once blood reaches the systematic capillaries, oxygen dissociates from hemoglobin (in RBC’s) which holds 97% of its maximum amount of O2 from normal air or holds 100% when breathing pure O2, diffuses through the red cell membranes into the plasma and from there into the tissue. We need O2 for the energy cycle that sustains life when we do not have enough O2 in our body tissues, series of events occur that, if not corrected, lead to disease conditions either infection, tissue destruction or both. If there is low O2 in tissues (hypoxia), there is a short window of opportunity to correct it.In addition to a large number of experimental studies numerous mathematical models[1,2,10] for the oxygen transport in the systematic capillaries and surrounding tissue in different organs of the body have been developed and analyzed. The first simple mathematical model for oxygen transport across the capillaries was formulated by Krogh . The model is based on the concept that oxygen diffuses only in to a tissue cylinder concentric with the capillary. Krogh has been used to investigate the oxygen transport in retinal capillary and surrounding tissues[8,9].Friedland[2]developed the mathematical model of transmural transport of oxygen to the retina of the human eye. He included not only the tissue metabolism and time varying concentrations but also included hydrostatic transmural pressure gradients in the model. The present work is concerned with the formulation of a simple mathematical model for the transport of oxygen from the retinal capillaries to the surrounding tissue. The equations governing the transport of intravascular oxygen in the retinal capillary and the transport of extravascular oxygen in the retinal tissue in a hypoxia environment are written in simplified form by taking into account the axial diffusion in the retinal tissue and capillary and an arbitrary oxyhemoglogbin dissociation relationship.
2. Mathematical Formulation
The illustration of physical model relevant to the present study is shown in Fig.1. The model comprises the single retinal capillary surrounded by a concentric cylinder of retinal tissue. In order to study the effect ofvarious parameters on the oxygen transport phenomena the model considers:ⅰ Oxygen transport in the retinal tissueⅱ Oxygen transport within the retinal capillaryThe model assumes that the radial and axial diffusion in the retinal tissue and the axial diffusion within the retinal capillary along with an arbitrary oxyhemoglobin dissociation relationship. The oxygen transported by the blood diffuses from the retinal capillary into retinal tissue and it is consumed at a constant rate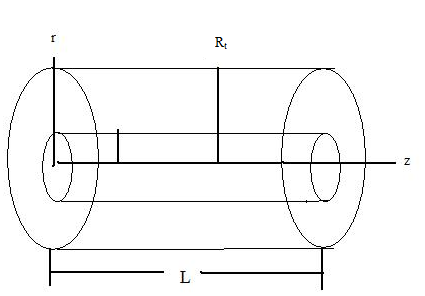 | Figure 1. Systematic diagram of oxygen transport into the retinal tissue |
In order to obtain the basic differential equationsgoverning the transport phenomena occurring in the tissue the following set of additional assumptions is introduced.
2.1. Assumptions
(ⅰ)A uniform radial oxygen distribution within the capillary.(ⅱ)The transport phenomena are steady.
2.2. Governing Equations
Retinal Tissue Region:By taking into account all the above mentioned assumptions, the oxygen concentration into the retinal tissue satisfies the equations in the form: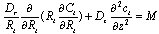 | (1) |
The above equation states that the oxygen concentration into the retinal tissue as a result of radial and axial diffusion into the retinal tissue. Where C represents the oxygen concentration in the retinal tissue,L capillary length, Rt radius of retinal tissue,M oxygen consumption rate, Dr, Dz radial and axial diffusivity.Capillary Region:The governing equation for the oxygen concentration within the capillary is given by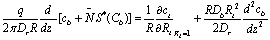 | (2) |
The above equation states that the oxygen of the blood changes along the capillary as a result of axial diffusion within the capillary and radial diffusion into the surrounding tissue. Where q is the volume blood flow rate , Db diffusivity of blood. Here oxygen content per unit of blood is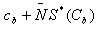 . Where the first term cb represents the dissolved oxygen and the second term
. Where the first term cb represents the dissolved oxygen and the second term 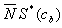 defines the oxygen bound to hemoglobin,
defines the oxygen bound to hemoglobin, 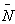 the oxygen capacity of blood at 100% saturation,
the oxygen capacity of blood at 100% saturation, 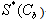 )is the oxyhemoglobin dissociation relationship.The function may
)is the oxyhemoglobin dissociation relationship.The function may 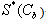 be approximated by the empirical formula
be approximated by the empirical formula | (3) |
for the suitable choice of the constants K and n.
2.3. Boundary Conditions
In order to formulate a physically consistent and mathematically tractable model, the boundary conditions relevant to the present problem are prescribed as follows:In tissue region: | (4) |
 | (5) |
The boundary condition (4) and (5) states that there will no permeation of oxygen along the radial and axial direction. Where C, R and z are prescribed.In capillary region: | (6) |
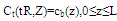 | (7) |
2.4. Non Dimensionalization
We define the non- dimensional variable by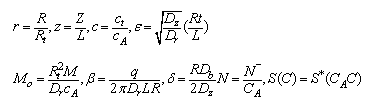 under the above scheme, Eqs. (1) and(2) for various regions are converted in the following normalized forms:along with the boundary condition’s
under the above scheme, Eqs. (1) and(2) for various regions are converted in the following normalized forms:along with the boundary condition’s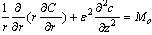 | (8) |
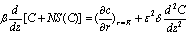 | (9) |
along with the boundary conditions: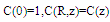 | (10) |
2.5. Solution to the Problem
In the present work we are interested in the study of effect of axial diffusion in the retinal capillary and tissue in the eye in order to ascertain when these effects can be neglected and when they must be taken in to account. The solutions of Eqs. (1)-(2) for the unknown function c(r,z) and C(z) with boundary conditions under different cases: (i) By setting €=0 and corresponds to neglecting axial diffusion in the retinal tissue and capillary. (ii) The effect of axial diffusion by considering the higher order terms (iii) Effect of radial and axial diffusion in the narrow region or boundary layer or near the ends. The above equations (8)and (9) may be solved for small € by using perturbation method. The solution for C(z) and c(r,z) will be obtained in the form of an asymptotic series, applicable for small €: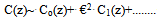 | (11) |
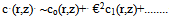 | (12) |
The leading term Co and co satisfy Eq.(8) and (10) with ε=0.Case (i): Without axial diffusion: In this case we consider the problem of finding C0(z) and c0(r,z) from Eqs. (8)-(8.1) and (9’) it follows that,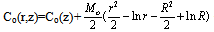 | (13) |
Substituting this into Eq.(9) and using the boundary condition (9’), it follows that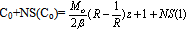 | (14) |
The above Equation gives z explicitly in terms of C0. For any choice of S(Co), z(Co) can be computed, starting at Co=1, where z=0,and continuing untill z=1 is attained.Case(ii): The effect of axial diffusion: We consider the problem of finding the functions C1(z)and c1(r,z) by substituting the expansions (11,12 ) into Eqs. (8), (8.1), (8.2),() and retaining term of order €2. Using the expansion S(Co+€2C1)=S(C0)+ €2S’(Co) C1, this gives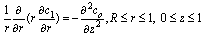 | (15) |
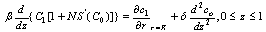 | (16) |
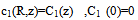 | (17) |
and includes the effect of axial diffusion. The solution to Eq.() satisfying the boundary condition is easily found to be 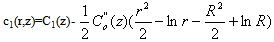 | (18) |
where C0(z) is already known from Eq.(14).Substituting this into Eq.(15) and integrating with respect to z gives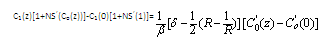 | (19) |
Using the boundary condition C1(0)=0 in Eq.(18) completes the solution for C1(z).The solution obtained in the form of expansion given by Eq.(11),(12) is not valid at the end z=0 because in the present analysis it has not been possible to satisfy the boundary condition expressed by Eq.(8.2), and the solution Co(z)+ε2C1(z) give nonzero O2flux through the ends of the cylinders. In order to determine the unknown constants C1(0) and complete the solution for C1(z) it is necessary to examine the solution in the region near z=0.THE SOLUTION NEAR z=0The boundary layer at the arterial end occupies a small region about z=0 in the limit 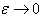 Therefore it cannot be described in terms of the physical variable z. The approximate boundary layer variable
Therefore it cannot be described in terms of the physical variable z. The approximate boundary layer variable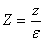 ,which has the property
,which has the property 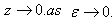 .In terms of this variable the governing equation are
.In terms of this variable the governing equation are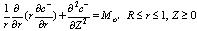 | (20) |
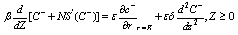 | (21) |
The boundary conditions are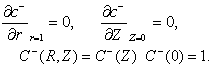 | (22) |
We write the solutions 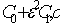 in terms of r and Z,and expanding the result in a series in
in terms of r and Z,and expanding the result in a series in 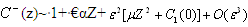 | (23) |
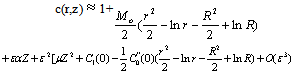 | (24) |
where 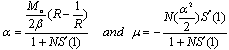 It can be shown that
It can be shown that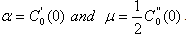 . It follows from Eq.(24) that the boundary layer expansion is of the form
. It follows from Eq.(24) that the boundary layer expansion is of the form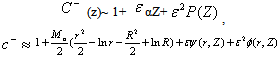 | (25) |
THE ARTERIAL BOUNDARY LAYERIn the previous section, we have obtained solution of order €2 for the capillary and retinal tissue oxygen concentration in the region bounded away from the arterial and venous ends.Thus, in this section, we have examined the asymptotic expansion near z=0 and the approximate analytical solutions to the governing equations are obtained in normalized forms by employing perturbation methods. From the expansion (20) we observed that to order €2 , the boundary layer expansions for the retinal capillary and tissue concentration are of the form given by(21),Where equations and boundary conditions for P and 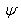 s were obtained above.Substituting the expansion (21) into the boundary layer equations gives the following problem for
s were obtained above.Substituting the expansion (21) into the boundary layer equations gives the following problem for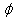 :
: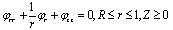 | (26) |
 | (27) |
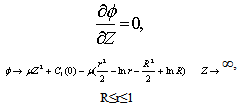 | (28) |
The problem for 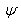 can be solved in terms of an eigen function expansion involving composite Bessel functions:
can be solved in terms of an eigen function expansion involving composite Bessel functions: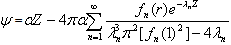 | (29) |
The eigenfunctions 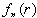 are defined in terms of the Bessel functions J0 and Yo by
are defined in terms of the Bessel functions J0 and Yo by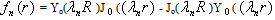 | (30) |
and the eigenvalues 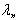 are the roots of
are the roots of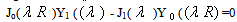 | (31) |
Here Jm, Ym denote the mth order Bessel functions of the first and second kind, respectively.From the Eq.() has no imaginary or repeated roots, and has an infinite number of positive roots The function P(Z) describing the retinal capillary oxygen concentration can be determined by substituting the solution fo ψ(r,Z) into Eq.(). This gives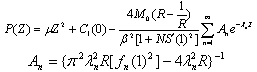 | (32) |
The solution to the Eq.() for φ is much more complex. Writing 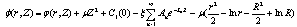 | (33) |
Where 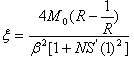 THE VENOUS BOUNDARY LAYER:The arterial boundary layer solution can be extended to the venous end. In this case the boundary layer variable is X=(1-z)/ε, which has the property z→1 as ε →0 for fixed X. In terms of this variable the governing equations are
THE VENOUS BOUNDARY LAYER:The arterial boundary layer solution can be extended to the venous end. In this case the boundary layer variable is X=(1-z)/ε, which has the property z→1 as ε →0 for fixed X. In terms of this variable the governing equations are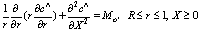 | (34) |
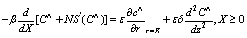 | (35) |
where 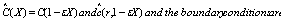
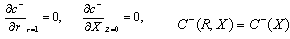 It can be shown that
It can be shown that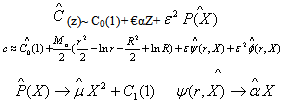
3. Results and Discussion
The values of most of model parameters are not known to the best of our knowledge. We have used appropriately estimated values of the physiological parameters in the computational model results. The computational results of the present model have been obtained from the above approximate solutions by using appropriate values of the physiological parameters listed in Table.1.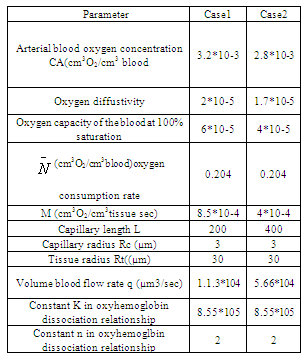 Case.I: It is observed from solutions that for the axial diffusion results in amore rapid decrease in the retinal capillary oxygen concentration at the arterial end and oxygen is delivered to the retinal tissue in excess of that necessary to meet its metabolic needs. This excess oxygen moves longitudinally in the retinal tissue.The curves in Fig.2 depict the retinal capillary concentration profiles both without axial diffusion and with axial diffusion for different values of tissue diffusivity. The solution without axial diffusion is independent of tissue diffusivity. As the diffusivity increases when the axial diffusion and the absolute value of €2C1(0) is increased.The extent of the deviation of the O2 profile from the solution directly related to the magnitude of €2C1(0) . In terms of dimensional variables
Case.I: It is observed from solutions that for the axial diffusion results in amore rapid decrease in the retinal capillary oxygen concentration at the arterial end and oxygen is delivered to the retinal tissue in excess of that necessary to meet its metabolic needs. This excess oxygen moves longitudinally in the retinal tissue.The curves in Fig.2 depict the retinal capillary concentration profiles both without axial diffusion and with axial diffusion for different values of tissue diffusivity. The solution without axial diffusion is independent of tissue diffusivity. As the diffusivity increases when the axial diffusion and the absolute value of €2C1(0) is increased.The extent of the deviation of the O2 profile from the solution directly related to the magnitude of €2C1(0) . In terms of dimensional variables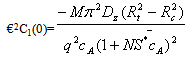 As €2C1(0)→0, the effect of axial diffusion on the oxygen profiles becomes negligible.sAs arterial O2 concentration decreases,
As €2C1(0)→0, the effect of axial diffusion on the oxygen profiles becomes negligible.sAs arterial O2 concentration decreases, 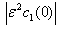 decreases and axial diffusion become less important. The curve in Fig.3(a,b) represents the effect of change in metabolic rate relative to data shown in table.1. These curves illustrate when the metabolic rate is increased, the value of
decreases and axial diffusion become less important. The curve in Fig.3(a,b) represents the effect of change in metabolic rate relative to data shown in table.1. These curves illustrate when the metabolic rate is increased, the value of 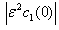 increased. Thus these curve illustrate the greater importance of axial diffusion at the arterial end.
increased. Thus these curve illustrate the greater importance of axial diffusion at the arterial end.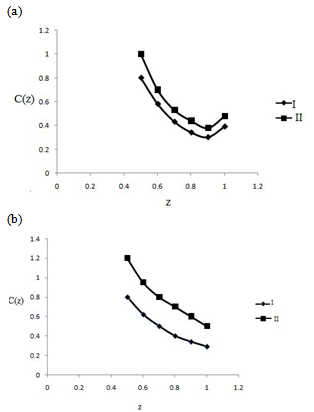 | Figure 2. The effect on the capillary oxygen concentration of changes in various parameters(a)Increased oxygen content of the arterial blood, (b) decreased oxygen content of the arterial blood (I) without axial diffusion, (II) with axial diffusion |
However, difference between the curves with and without axial diffusion in these figures are comparable in the midcapillary region. From the factor[1+NS’C0(z)], C1(z) decreases, with distance z as the slope of the oxyhemoglobin relationship increases. The more amount of oxygen consumed in the retinal tissue to move from the relatively flat portion of the dissociation curve to the very step portion. Thus there should be a significant decrease in 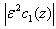 along the capillary length. However while
along the capillary length. However while 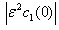 is greater in Fig.3(b) decreases to much smaller values of
is greater in Fig.3(b) decreases to much smaller values of 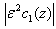 as the lower oxygen concentration is observed. Thus, the non-linearity of the oxyhemoglobin dissociation relationship plays an important role in determining the difference between the solution with and without axial diffusion.
as the lower oxygen concentration is observed. Thus, the non-linearity of the oxyhemoglobin dissociation relationship plays an important role in determining the difference between the solution with and without axial diffusion. 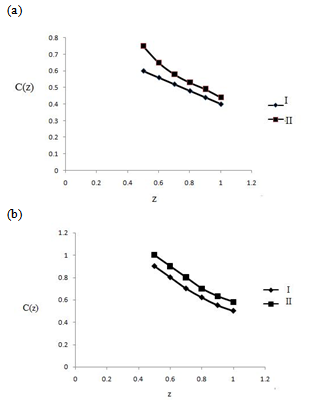 | Figure 3. The effect on the capillary oxygen concentration of changes in (a) decreased oxygen consumption rate (b) increased oxygen consumption rate; (I) without axial diffusion,(II)with axial diffusion |
References
| [1] | B. Allan Friedland, (1978) ‘ Mathematical model of transmural transport of oxygen to the retina’, Bull. Math. Biol.Vol 40, pp 823–837. |
| [2] | .J. Mcguire and T.W. Secomb,(2001) ‘A theoretical model for oxygen transport in skeletal muscle under conditions of high oxygen demand’,Appl. Physiol. Vol91, pp 2255–2265. |
| [3] | Cringle Stephen J, Yu D (2004). Intraretinal oxygenation and oxygen consumption in the rabbit during systemic hyperoxia. Invest Ophthalmol. Vis. Sci. Vol 45 pp.3223-3228 |
| [4] | Haugh LM, Linsenmeier RA and Goldstick TK. (1990). Mathematical models of the spatial distribution of retinal oxygen tension Ann.Biomed.Eng. Vol 18,pp.19-36 |
| [5] | M. Sharan, M.P. Singh,and B. Singh, (1995)’An analytical model for oxygen transport in tissue capillaries in a hyperbaric environment with first order metabolic consumption’, Math. Comput. Modell. Vol 22 (9) pp. 99–111. |
| [6] | Marshall Mun, Shin Lih, (1975) Transport Phenomena in Medicine and Biology’, John Wiley and Sons, New York,. |
| [7] | Pakola SJand Grunwald JE (1993): Effects of oxygen and carbon dioxide on humanretinal circulation. Invest Ophthalmol Vis Sci Vol. 34, pp. 2866-2870. |
| [8] | R. Kumar, F. Stepanek, A. Mantalaris, (2004), An oxygen transport model to bone narrow microcirculation’, Food Bioprod. Process. Vol82, pp.105–116. |
| [9] | Remington LA. (2005).Clinical Anatomy of the Visual System. 2nd Edition ed. St. Louis,Missouri: Elsevier, |
| [10] | Roos W. Magnus,( 2004), Theoretical estimation of retinal oxygenation during retinal artery occulsion’, Physiol. Meas. Vol 25 pp.1523–1532. |


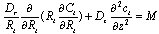
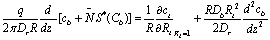
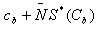 . Where the first term cb represents the dissolved oxygen and the second term
. Where the first term cb represents the dissolved oxygen and the second term 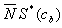 defines the oxygen bound to hemoglobin,
defines the oxygen bound to hemoglobin, 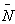 the oxygen capacity of blood at 100% saturation,
the oxygen capacity of blood at 100% saturation, 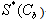 )is the oxyhemoglobin dissociation relationship.The function may
)is the oxyhemoglobin dissociation relationship.The function may 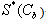 be approximated by the empirical formula
be approximated by the empirical formula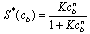
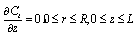
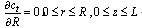
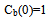
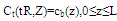
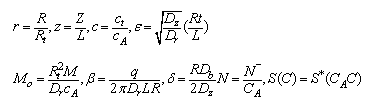 under the above scheme, Eqs. (1) and(2) for various regions are converted in the following normalized forms:along with the boundary condition’s
under the above scheme, Eqs. (1) and(2) for various regions are converted in the following normalized forms:along with the boundary condition’s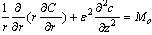
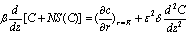
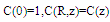
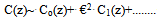
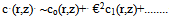
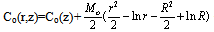
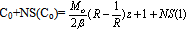
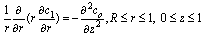
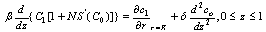
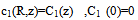
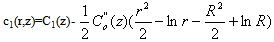
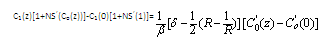
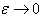 Therefore it cannot be described in terms of the physical variable z. The approximate boundary layer variable
Therefore it cannot be described in terms of the physical variable z. The approximate boundary layer variable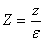 ,which has the property
,which has the property 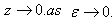 .In terms of this variable the governing equation are
.In terms of this variable the governing equation are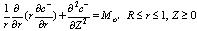
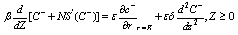
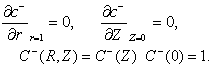
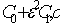 in terms of r and Z,and expanding the result in a series in
in terms of r and Z,and expanding the result in a series in 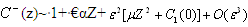
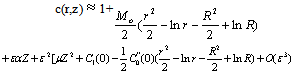
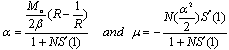 It can be shown that
It can be shown that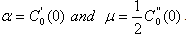 . It follows from Eq.(24) that the boundary layer expansion is of the form
. It follows from Eq.(24) that the boundary layer expansion is of the form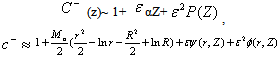
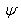 s were obtained above.Substituting the expansion (21) into the boundary layer equations gives the following problem for
s were obtained above.Substituting the expansion (21) into the boundary layer equations gives the following problem for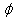 :
: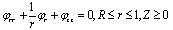

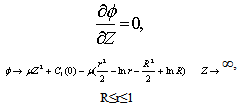
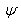 can be solved in terms of an eigen function expansion involving composite Bessel functions:
can be solved in terms of an eigen function expansion involving composite Bessel functions: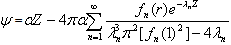
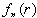 are defined in terms of the Bessel functions J0 and Yo by
are defined in terms of the Bessel functions J0 and Yo by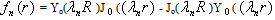
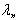 are the roots of
are the roots of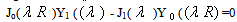
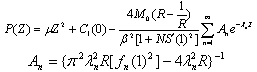
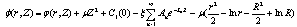
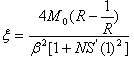 THE VENOUS BOUNDARY LAYER:The arterial boundary layer solution can be extended to the venous end. In this case the boundary layer variable is X=(1-z)/ε, which has the property z→1 as ε →0 for fixed X. In terms of this variable the governing equations are
THE VENOUS BOUNDARY LAYER:The arterial boundary layer solution can be extended to the venous end. In this case the boundary layer variable is X=(1-z)/ε, which has the property z→1 as ε →0 for fixed X. In terms of this variable the governing equations are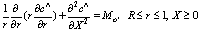
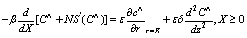
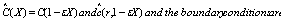
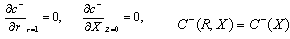 It can be shown that
It can be shown that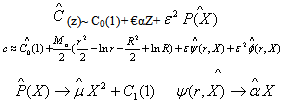
 Case.I: It is observed from solutions that for the axial diffusion results in amore rapid decrease in the retinal capillary oxygen concentration at the arterial end and oxygen is delivered to the retinal tissue in excess of that necessary to meet its metabolic needs. This excess oxygen moves longitudinally in the retinal tissue.The curves in Fig.2 depict the retinal capillary concentration profiles both without axial diffusion and with axial diffusion for different values of tissue diffusivity. The solution without axial diffusion is independent of tissue diffusivity. As the diffusivity increases when the axial diffusion and the absolute value of €2C1(0) is increased.The extent of the deviation of the O2 profile from the solution directly related to the magnitude of €2C1(0) . In terms of dimensional variables
Case.I: It is observed from solutions that for the axial diffusion results in amore rapid decrease in the retinal capillary oxygen concentration at the arterial end and oxygen is delivered to the retinal tissue in excess of that necessary to meet its metabolic needs. This excess oxygen moves longitudinally in the retinal tissue.The curves in Fig.2 depict the retinal capillary concentration profiles both without axial diffusion and with axial diffusion for different values of tissue diffusivity. The solution without axial diffusion is independent of tissue diffusivity. As the diffusivity increases when the axial diffusion and the absolute value of €2C1(0) is increased.The extent of the deviation of the O2 profile from the solution directly related to the magnitude of €2C1(0) . In terms of dimensional variables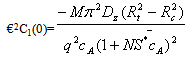 As €2C1(0)→0, the effect of axial diffusion on the oxygen profiles becomes negligible.sAs arterial O2 concentration decreases,
As €2C1(0)→0, the effect of axial diffusion on the oxygen profiles becomes negligible.sAs arterial O2 concentration decreases, 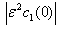 decreases and axial diffusion become less important. The curve in Fig.3(a,b) represents the effect of change in metabolic rate relative to data shown in table.1. These curves illustrate when the metabolic rate is increased, the value of
decreases and axial diffusion become less important. The curve in Fig.3(a,b) represents the effect of change in metabolic rate relative to data shown in table.1. These curves illustrate when the metabolic rate is increased, the value of 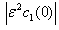 increased. Thus these curve illustrate the greater importance of axial diffusion at the arterial end.
increased. Thus these curve illustrate the greater importance of axial diffusion at the arterial end.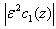 along the capillary length. However while
along the capillary length. However while 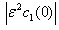 is greater in Fig.3(b) decreases to much smaller values of
is greater in Fig.3(b) decreases to much smaller values of 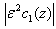 as the lower oxygen concentration is observed. Thus, the non-linearity of the oxyhemoglobin dissociation relationship plays an important role in determining the difference between the solution with and without axial diffusion.
as the lower oxygen concentration is observed. Thus, the non-linearity of the oxyhemoglobin dissociation relationship plays an important role in determining the difference between the solution with and without axial diffusion.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
