J.I. Mamedkhanov1, I.B. Dadashova2
1Department of theory of functions and functional analysis, Baku State University, Baku, AZ 1148, Azerbaijan
21Department of theory of functions and functional analysis, Baku State University, Baku, AZ 1148, Azerbaijan
Correspondence to: J.I. Mamedkhanov, Department of theory of functions and functional analysis, Baku State University, Baku, AZ 1148, Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we study a problem of approximation for the classes of functions determined only on the boundary of domain in weighted integral spaces by means of the rational functions of the form (1) where 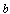 is a point lying strictly inside the considered curve. Notice that the approximation estimations, generally speaking, coincide with the estimations of polynomial approximation for
is a point lying strictly inside the considered curve. Notice that the approximation estimations, generally speaking, coincide with the estimations of polynomial approximation for 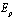 classes (Smirnov's class).
classes (Smirnov's class).
Keywords:
Rational Approximation, Conformal Map, Smoothness Modulus
1. Introduction
Approximation problem for the classes of functions determined only on the boundary of domain is of great importance alongside with the study of approximation of functions by means of polynomials analytic in the domain 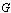 and with some conditions on the boundary
and with some conditions on the boundary 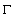 . Obviously, it is impossible in general to approximate such classes of functions by means of polynomials[12]. Therefore, various kinds of rational functions or so called generalized polynomials are mostly used in this case as an approximation tool[12]. J. I. Mamedkhanov, D. M. Israfilov and I. M. Botchaev investigated the approximation problems of functions determined only on the boundary of domain by means of rational functions of the form
. Obviously, it is impossible in general to approximate such classes of functions by means of polynomials[12]. Therefore, various kinds of rational functions or so called generalized polynomials are mostly used in this case as an approximation tool[12]. J. I. Mamedkhanov, D. M. Israfilov and I. M. Botchaev investigated the approximation problems of functions determined only on the boundary of domain by means of rational functions of the form 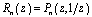 for certain classes of curves in terms of uniform metric[1-4].In this paper, we study the approximation problems of a function from the class
for certain classes of curves in terms of uniform metric[1-4].In this paper, we study the approximation problems of a function from the class 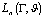 by means of a rational function of the form
by means of a rational function of the form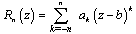 | (1) |
where 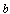 is a point lying strictly inside the considered curve
is a point lying strictly inside the considered curve 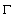 1. Without loss of generality, we will assume
1. Without loss of generality, we will assume 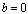 throughout this paper.
throughout this paper.
2. Basic Definitions and Notations
1. Let 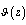 be an almost everywhere finite, non-zerofunction measurable on
be an almost everywhere finite, non-zerofunction measurable on 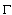 . If the function
. If the function 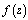 determined on
determined on 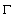 is measurable, and the function
is measurable, and the function 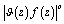 the class
the class 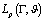 . If we define the norm in the class
. If we define the norm in the class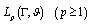 as
as 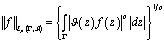 , then is integrable on
, then is integrable on 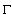 , then we will say that
, then we will say that 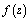 belongs to
belongs to 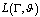 becomes a Banach space
becomes a Banach space 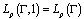 .2. By
.2. By 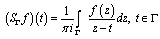 we denote the Cauchy singular integral.3. Denote by
we denote the Cauchy singular integral.3. Denote by 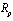 a totality of curves
a totality of curves 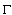 for which
for which 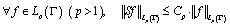 , where
, where 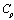 is depending on the point
is depending on the point 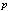 .Notice that the classes
.Notice that the classes 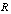 and
and 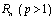 are equivalent[5].4. Let
are equivalent[5].4. Let 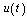 be a measurable, almost everywhere finite function on
be a measurable, almost everywhere finite function on 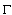 . We will say that
. We will say that 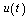 belongs to the class
belongs to the class 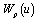 if it differs from zero almost everywhere and the operator
if it differs from zero almost everywhere and the operator 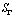 is bounded in the space
is bounded in the space 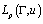 . Notice that this class is well studied in the theory of singular operators[5]. 5. We will say that the closed curve
. Notice that this class is well studied in the theory of singular operators[5]. 5. We will say that the closed curve 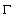 belongs to the class
belongs to the class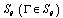 if
if 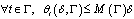 where
where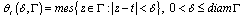 26. We will say that the curve
26. We will say that the curve 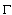 belongs to the class of
belongs to the class of 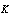 -curves
-curves 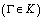 if the length of the greatest of the arches connecting two arbitrary points
if the length of the greatest of the arches connecting two arbitrary points 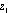 and
and 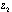 on it has the same order as that of the chord connecting these points[10-11].Obviously,
on it has the same order as that of the chord connecting these points[10-11].Obviously, 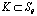 .A lot of works have been devoted to the class of curves
.A lot of works have been devoted to the class of curves 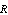 over the past years[5]. Finally, G. David[6] proved that
over the past years[5]. Finally, G. David[6] proved that 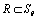 .7. By
.7. By 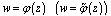 we will denote a function that conformally and univalently maps the exterior (interior) of the curve
we will denote a function that conformally and univalently maps the exterior (interior) of the curve 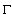 onto the exterior (interior) of a unit circle
onto the exterior (interior) of a unit circle 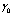 normalized by the conditions:
normalized by the conditions: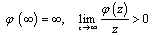 ,and let
,and let 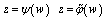 denote the inverse to function to
denote the inverse to function to 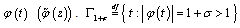 is a level line of the curve
is a level line of the curve 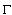 ;
; 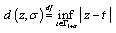 for
for 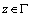 ;
; 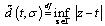 for
for 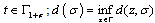 .8. Let’s consider the following quantities (see[7]):where
.8. Let’s consider the following quantities (see[7]):where 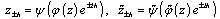 .Obviously, these quantities satisfy all the properties of smoothness modulus on good classes of curves, in particular, on smooth or piecewise-smooth curves. In case of more general classes of curves we will consider the quantitiesandProceeding in the same way as in[7], it is easy to see that these quantities satisfy all the properties of smoothness modulus (i.e.
.Obviously, these quantities satisfy all the properties of smoothness modulus on good classes of curves, in particular, on smooth or piecewise-smooth curves. In case of more general classes of curves we will consider the quantitiesandProceeding in the same way as in[7], it is easy to see that these quantities satisfy all the properties of smoothness modulus (i.e. 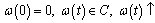 ,
, 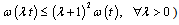 on any curves
on any curves 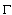 and they are the best majorants for the functions
and they are the best majorants for the functions 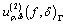 and
and 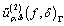 , respectively, among all smoothness modulus type functions.
, respectively, among all smoothness modulus type functions.
3. Main Result
Now we prove the following:Theorem. Let 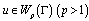 and
and 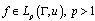 . Then, for every positive integer
. Then, for every positive integer 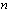 there exists a rational function
there exists a rational function 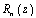 of the form (1) such that
of the form (1) such that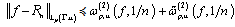 .3
.3
4. Proof
Obviously, 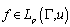 and
and 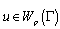 imply that
imply that 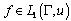 . Now, by virtue of
. Now, by virtue of 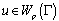 we can state that
we can state that 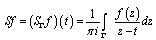 exists almost everywhere on
exists almost everywhere on 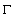 . It follows that[8], the Cauchy type integral has certain angular values almost everywhere on
. It follows that[8], the Cauchy type integral has certain angular values almost everywhere on 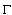 equal to
equal to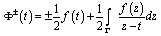 .And this in turn implies thatThis relation shows that in order to approximate the function
.And this in turn implies thatThis relation shows that in order to approximate the function 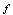 given only on the curve
given only on the curve 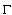 in terms of the metric of the space
in terms of the metric of the space 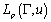 it suffices to approximate the functions
it suffices to approximate the functions 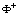 and
and 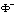 which are analytic inside and outside the given closed curve, respectively, and belong to
which are analytic inside and outside the given closed curve, respectively, and belong to 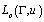 . So let us prove that for every positive integer
. So let us prove that for every positive integer  there exist the polynomials
there exist the polynomials 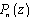 and
and 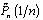 of degree
of degree 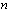 such that
such that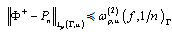 | (3) |
and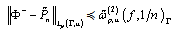 | (4) |
First we will prove the validity of relation (3). From 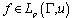 and
and 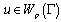 it follows that if
it follows that if 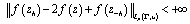 ,then
,then 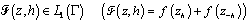 . This allows to state that the singular integral
. This allows to state that the singular integral 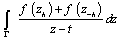 exists almost everywhere on
exists almost everywhere on 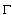 in the sense of principal value. The last statement enables us to approximate the function
in the sense of principal value. The last statement enables us to approximate the function 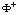 by the Jackson-Dzyadyk polynomials[9] represented in the following form:
by the Jackson-Dzyadyk polynomials[9] represented in the following form: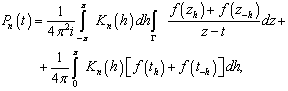 | (5) |
where 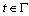 and
and 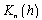 is a kernel that represents a trigonometric polynomial of at most
is a kernel that represents a trigonometric polynomial of at most 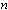 -th degree and satisfies the conditions
-th degree and satisfies the conditions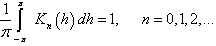 | (6) |
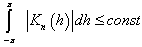 | (7) |
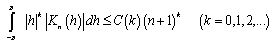 | (8) |
Furthermore, from fulfillment of conditions (6) - (8) we directly get 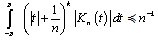 | (9) |
Now, taking into account relation (6), we represent the function 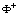 as follows:
as follows: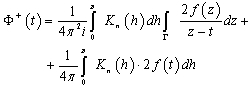 | (10) |
Further, by virtue of relations (5) and (10), we estimate the difference 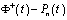 in the sense of
in the sense of  metric. Obviously, we have
metric. Obviously, we have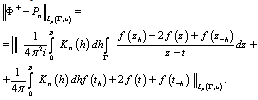 We apply Minkovski inequality, and then Minkovski’s generalized inequality to find that
We apply Minkovski inequality, and then Minkovski’s generalized inequality to find that 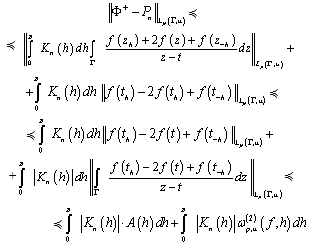 (11) where
(11) where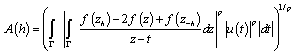 As
As 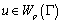 , the latter relation yields
, the latter relation yields 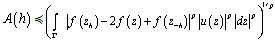 It follows from (11) that
It follows from (11) that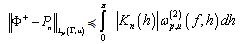 | (12) |
Therefore, using classical technique we get (3).To complete the proof, we only have to show the validity of relation (4). To this end, we map the plane  onto the plane
onto the plane  by means of the function
by means of the function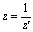 | (13) |
Obviously, the contour 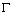 is mapped into some contour
is mapped into some contour 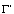 and the functions
and the functions 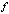 and
and 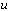 are transformed into the functions
are transformed into the functions 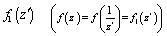 and
and 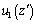
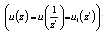 , respectively.Let us prove the validity of the following statements:
, respectively.Let us prove the validity of the following statements: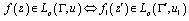 | (14) |
andValidity of (14) is obvious.Further, combining relation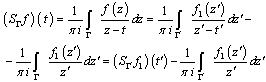 | (16) |
with relation (14) and the fact that 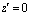 lies strictly outside
lies strictly outside  , we get relation (15).At the same time, we notice that for
, we get relation (15).At the same time, we notice that for 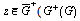 is the interior of the curve
is the interior of the curve 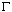 ) the function
) the function 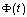 on the plane
on the plane 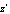 takes the form
takes the form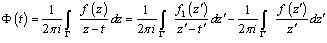 .If we take into accountthen we get:Obviously, the function
.If we take into accountthen we get:Obviously, the function 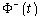 in the plane
in the plane 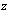 corresponds to the function
corresponds to the function 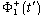 in the plane
in the plane 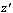 . Hence, by virtue of relation (3) we get
. Hence, by virtue of relation (3) we get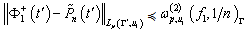 | (17) |
Further, taking into account that 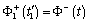 ,
, 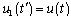 and the point
and the point 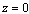 lies inside
lies inside 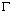 , we get
, we get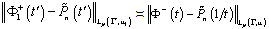 | (18) |
To complete the proof of relation (4) we use the obvious relation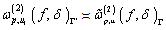 | (19) |
Thus, from relation (17), by virtue of (18) and (19), we get the required relation (4).Now, to complete the proof of the theorem it suffices to make use of relations (3) and (4) and for 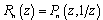 ,from whence, by virtue of relation (2), the statement of theorem follows.
,from whence, by virtue of relation (2), the statement of theorem follows.
Notes
1. By 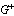 and
and 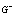 we will denote an interior and an exterior of the curve
we will denote an interior and an exterior of the curve 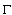 , respectively.2.
, respectively.2. 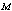 denotes various positive constants depending only on explicit parameters. In addition, we will use the notations
denotes various positive constants depending only on explicit parameters. In addition, we will use the notations 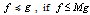 and
and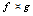 , if
, if 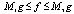 .3. Signs ≼ and ≍ define an ordinal relation. Namely,
.3. Signs ≼ and ≍ define an ordinal relation. Namely, 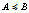 means
means 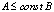 . And
. And 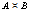 means
means 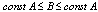 .
.
References
| [1] | J. I. Mamedkhanov, D. M. Isralov, “Approximation by rational functions of polynomials on curves”, Doklady Mathematics Azerb., vol. 35, no.4, pp. 19-20, 1979. |
| [2] | J. I. Mamedkhanov, I. M. Batchayev, “The problems on approximation on a uniform metric on quasiconformal curves,” Proceedings of the I Republican scientific Conference of post-graduate students of Azerbaijan, Azerbaijan, Baku, 1978. |
| [3] | D. I. Mamedkhanov, “Weighted Approximation in the mean,” In the book: Abstracts of the International Conference on the Constructive Theory of Functions, Sofia, 1977. |
| [4] | D. I. Mamedkhanov, “Weighted polynomial approximation in the mean on a complex plane,” In Proceedings of the all union Shool: Modern problems of theory of functions, Azerbaijan, Baku, 1977, pp. 169-180, 1980. |
| [5] | B. V. Khvedelidze, “The method of Cauchy type integral in discontinuous boundary value problems,” Contemporary problems of mathematics, Itogi Nauki, Math., no. 7, pp. 5-163, 1975. |
| [6] | G. David, “Gourbes cordeare et espaces de Hardy generalises”, Ann. Just. Fourier, Vol. 32, No. 3, pp. 227-239, 1982. |
| [7] | J. I. Mamedkhanov, I. B. Dadashova, “Analogue of Jackson-Bernstein's theorem in on closed curves in the complex plane II,” Further progress in analysis, in Proceedings of the 6th International ISAAC Congress, Ankara, Turkey, 13-18 August 2007, World Scientific, pp. 260-267, 2009. |
| [8] | I. I. Privalov, Boundary properties of single-valued analytic fufunctions, Nauka, Moscow , (Russian), 1950. |
| [9] | V. K. Dzyadyk, Introduction to the theory of approximation of functions by polynomials, Nauka, Moscow (Russian), 1977. |
| [10] | V. V. Andrievskii, “Weighted polynomial inequalities with doubling weights on a quasismooth arc”. Acta Mathematica Hungarica, vol. 135, no.1-2, pp.8-23, 2012, DOI: 10.1007/s10474-011-0155-6). |
| [11] | V. V. Andrievskii, “Weighted Bernstein-type inequalities on a quasismooth curve in the complex plane”. Constructive Approximation. 2011, DOI: 10.1007/s00365-011-9144-9. |
| [12] | A. A. Gonchar, “Rational approximation of analytic functions”, Linear and complex analysis problems, Lect. Notes Math., 1043, eds. V.P. Havin, S. V. Hruscev, N. K. Nikol’sci, Springer, pp.471–474, 1982. |

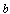 is a point lying strictly inside the considered curve. Notice that the approximation estimations, generally speaking, coincide with the estimations of polynomial approximation for
is a point lying strictly inside the considered curve. Notice that the approximation estimations, generally speaking, coincide with the estimations of polynomial approximation for 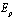 classes (Smirnov's class).
classes (Smirnov's class).
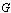 and with some conditions on the boundary
and with some conditions on the boundary 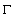 . Obviously, it is impossible in general to approximate such classes of functions by means of polynomials[12]. Therefore, various kinds of rational functions or so called generalized polynomials are mostly used in this case as an approximation tool[12]. J. I. Mamedkhanov, D. M. Israfilov and I. M. Botchaev investigated the approximation problems of functions determined only on the boundary of domain by means of rational functions of the form
. Obviously, it is impossible in general to approximate such classes of functions by means of polynomials[12]. Therefore, various kinds of rational functions or so called generalized polynomials are mostly used in this case as an approximation tool[12]. J. I. Mamedkhanov, D. M. Israfilov and I. M. Botchaev investigated the approximation problems of functions determined only on the boundary of domain by means of rational functions of the form 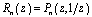 for certain classes of curves in terms of uniform metric[1-4].In this paper, we study the approximation problems of a function from the class
for certain classes of curves in terms of uniform metric[1-4].In this paper, we study the approximation problems of a function from the class 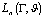 by means of a rational function of the form
by means of a rational function of the form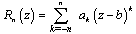
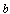 is a point lying strictly inside the considered curve
is a point lying strictly inside the considered curve 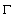 1. Without loss of generality, we will assume
1. Without loss of generality, we will assume 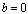 throughout this paper.
throughout this paper. be an almost everywhere finite, non-zerofunction measurable on
be an almost everywhere finite, non-zerofunction measurable on 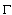 . If the function
. If the function 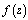 determined on
determined on 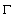 is measurable, and the function
is measurable, and the function 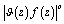 the class
the class 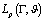 . If we define the norm in the class
. If we define the norm in the class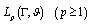 as
as 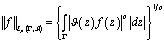 , then is integrable on
, then is integrable on 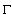 , then we will say that
, then we will say that 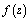 belongs to
belongs to 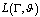 becomes a Banach space
becomes a Banach space 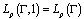 .2. By
.2. By 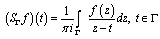 we denote the Cauchy singular integral.3. Denote by
we denote the Cauchy singular integral.3. Denote by 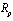 a totality of curves
a totality of curves 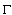 for which
for which 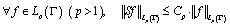 , where
, where 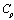 is depending on the point
is depending on the point 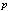 .Notice that the classes
.Notice that the classes 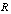 and
and 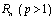 are equivalent[5].4. Let
are equivalent[5].4. Let 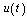 be a measurable, almost everywhere finite function on
be a measurable, almost everywhere finite function on 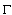 . We will say that
. We will say that 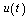 belongs to the class
belongs to the class 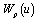 if it differs from zero almost everywhere and the operator
if it differs from zero almost everywhere and the operator 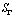 is bounded in the space
is bounded in the space 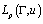 . Notice that this class is well studied in the theory of singular operators[5]. 5. We will say that the closed curve
. Notice that this class is well studied in the theory of singular operators[5]. 5. We will say that the closed curve 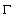 belongs to the class
belongs to the class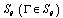 if
if 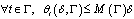 where
where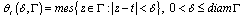 26. We will say that the curve
26. We will say that the curve 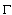 belongs to the class of
belongs to the class of 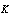 -curves
-curves 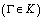 if the length of the greatest of the arches connecting two arbitrary points
if the length of the greatest of the arches connecting two arbitrary points 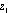 and
and 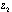 on it has the same order as that of the chord connecting these points[10-11].Obviously,
on it has the same order as that of the chord connecting these points[10-11].Obviously, 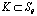 .A lot of works have been devoted to the class of curves
.A lot of works have been devoted to the class of curves 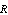 over the past years[5]. Finally, G. David[6] proved that
over the past years[5]. Finally, G. David[6] proved that 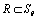 .7. By
.7. By 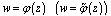 we will denote a function that conformally and univalently maps the exterior (interior) of the curve
we will denote a function that conformally and univalently maps the exterior (interior) of the curve 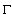 onto the exterior (interior) of a unit circle
onto the exterior (interior) of a unit circle 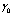 normalized by the conditions:
normalized by the conditions: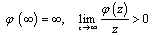 ,and let
,and let 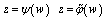 denote the inverse to function to
denote the inverse to function to 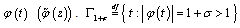 is a level line of the curve
is a level line of the curve 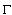 ;
; 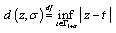 for
for 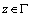 ;
; 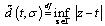 for
for 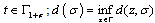 .8. Let’s consider the following quantities (see[7]):where
.8. Let’s consider the following quantities (see[7]):where 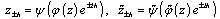 .Obviously, these quantities satisfy all the properties of smoothness modulus on good classes of curves, in particular, on smooth or piecewise-smooth curves. In case of more general classes of curves we will consider the quantitiesandProceeding in the same way as in[7], it is easy to see that these quantities satisfy all the properties of smoothness modulus (i.e.
.Obviously, these quantities satisfy all the properties of smoothness modulus on good classes of curves, in particular, on smooth or piecewise-smooth curves. In case of more general classes of curves we will consider the quantitiesandProceeding in the same way as in[7], it is easy to see that these quantities satisfy all the properties of smoothness modulus (i.e. 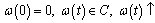 ,
, 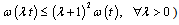 on any curves
on any curves 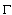 and they are the best majorants for the functions
and they are the best majorants for the functions 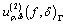 and
and 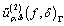 , respectively, among all smoothness modulus type functions.
, respectively, among all smoothness modulus type functions. 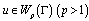 and
and 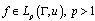 . Then, for every positive integer
. Then, for every positive integer 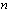 there exists a rational function
there exists a rational function 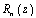 of the form (1) such that
of the form (1) such that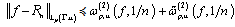 .3
.3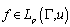 and
and 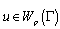 imply that
imply that 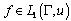 . Now, by virtue of
. Now, by virtue of 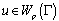 we can state that
we can state that 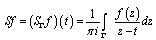 exists almost everywhere on
exists almost everywhere on 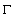 . It follows that[8], the Cauchy type integral has certain angular values almost everywhere on
. It follows that[8], the Cauchy type integral has certain angular values almost everywhere on 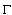 equal to
equal to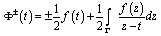 .And this in turn implies thatThis relation shows that in order to approximate the function
.And this in turn implies thatThis relation shows that in order to approximate the function 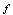 given only on the curve
given only on the curve 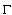 in terms of the metric of the space
in terms of the metric of the space 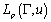 it suffices to approximate the functions
it suffices to approximate the functions 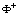 and
and 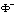 which are analytic inside and outside the given closed curve, respectively, and belong to
which are analytic inside and outside the given closed curve, respectively, and belong to 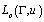 . So let us prove that for every positive integer
. So let us prove that for every positive integer  there exist the polynomials
there exist the polynomials 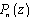 and
and 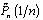 of degree
of degree 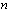 such that
such that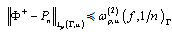
 and
and  it follows that if
it follows that if  ,then
,then 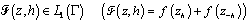 . This allows to state that the singular integral
. This allows to state that the singular integral 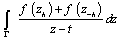 exists almost everywhere on
exists almost everywhere on 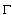 in the sense of principal value. The last statement enables us to approximate the function
in the sense of principal value. The last statement enables us to approximate the function  by the Jackson-Dzyadyk polynomials[9] represented in the following form:
by the Jackson-Dzyadyk polynomials[9] represented in the following form:
 and
and  is a kernel that represents a trigonometric polynomial of at most
is a kernel that represents a trigonometric polynomial of at most  -th degree and satisfies the conditions
-th degree and satisfies the conditions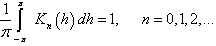
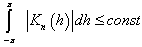
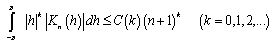
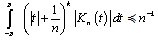
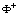 as follows:
as follows: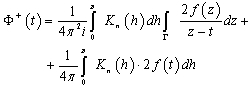
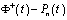 in the sense of
in the sense of 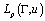 metric. Obviously, we have
metric. Obviously, we have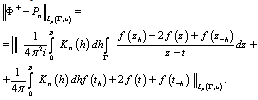 We apply Minkovski inequality, and then Minkovski’s generalized inequality to find that
We apply Minkovski inequality, and then Minkovski’s generalized inequality to find that 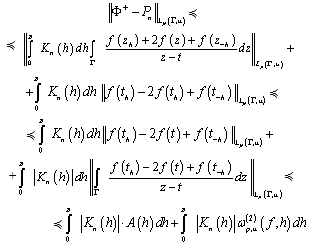 (11) where
(11) where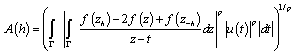 As
As 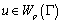 , the latter relation yields
, the latter relation yields 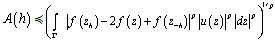 It follows from (11) that
It follows from (11) that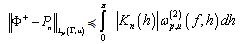
 onto the plane
onto the plane  by means of the function
by means of the function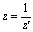
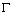 is mapped into some contour
is mapped into some contour 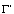 and the functions
and the functions 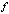 and
and 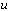 are transformed into the functions
are transformed into the functions 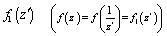 and
and 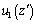
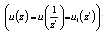 , respectively.Let us prove the validity of the following statements:
, respectively.Let us prove the validity of the following statements: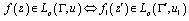
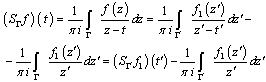
 lies strictly outside
lies strictly outside  , we get relation (15).At the same time, we notice that for
, we get relation (15).At the same time, we notice that for 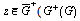 is the interior of the curve
is the interior of the curve 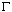 ) the function
) the function 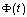 on the plane
on the plane 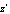 takes the form
takes the form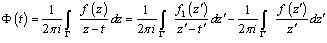 .If we take into accountthen we get:Obviously, the function
.If we take into accountthen we get:Obviously, the function 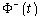 in the plane
in the plane 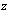 corresponds to the function
corresponds to the function 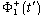 in the plane
in the plane 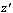 . Hence, by virtue of relation (3) we get
. Hence, by virtue of relation (3) we get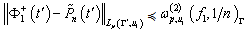
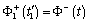 ,
, 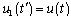 and the point
and the point 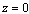 lies inside
lies inside 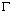 , we get
, we get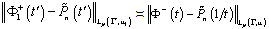
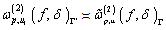
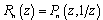 ,from whence, by virtue of relation (2), the statement of theorem follows.
,from whence, by virtue of relation (2), the statement of theorem follows. and
and  we will denote an interior and an exterior of the curve
we will denote an interior and an exterior of the curve  , respectively.2.
, respectively.2. 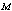 denotes various positive constants depending only on explicit parameters. In addition, we will use the notations
denotes various positive constants depending only on explicit parameters. In addition, we will use the notations 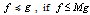 and
and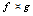 , if
, if 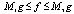 .3. Signs ≼ and ≍ define an ordinal relation. Namely,
.3. Signs ≼ and ≍ define an ordinal relation. Namely, 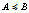 means
means 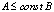 . And
. And 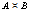 means
means 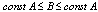 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML