-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(3): 70-76
doi: 10.5923/j.am.20120203.05
Unsteady Three Dimensional Free Convection Heat and Mass Transfer Flow Embedded in a Porous Medium with Periodic Permeability and Constant Heat and Mass Flux
N. C. Jain, D. Chaudhary, Dinesh K. Vijay
Department of Mathematics, University of Rajasthan, Jaipur-302004
Correspondence to: N. C. Jain, Department of Mathematics, University of Rajasthan, Jaipur-302004.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We analyse an unsteady three dimensional free convection flow with combined heat and mass transfer over a vertical plate embedded in a porous medium with time dependent suction velocity and transverse sinusoidal permeability. The unsteadiness is due to the time dependent suction velocity. The governing equations with the boundary conditions are first converted into dimensionless form by non-similar transformations and then resulting system of coupled non-linear partial differential equations are solved by series expansion method. The effects of different parameters are shown on velocity (u), cross flow velocity (w), temperature (θ), Concentration (C), Skin friction (τx) and Nusselt number (Nu) graphically. We observe that skin friction is higher in air (Pr=0.71) than in water (Pr=7) but result differs for Nusselt number.
Keywords: Free convection, Heat flux, Mass flux, Porous medium, Three dimensional and Unsteady
Article Outline
1. Introduction
- The phenomenon of free convective flow with simultaneous heat and mass transfer has been a subject of interest of many researchers because of its varied applications in natural sciences, engineering sciences and in industry. Such phenomenon is observed in buoyancy induced motions in the atmosphere, in bodies of water, quasi-solid bodies such as earth, etc. Free convective flows with periodic permeability through highly porous media play an important role in chemical engineering, turbo-machinery and in aerospace technology. Such flow include several practical applications, for example, geothermal reservoirs, drying of porous solids, thermal insulation, enhanced oil recovery, packed-bed catalytic reactors, cooling of nuclear reactors and underground energy transport.In view of these applications various investigators have worked on the subject but restricted themselves to two dimensional flows. But situations may arise when the flow field may be essentially three dimensional, for example, when suction velocity, porous medium, temperature on the body etc. varies sinusoidaly. Ahmed[2] has studied heat and mass transfer on free convective three dimensional unsteady flows over a porous vertical plate. Aboeldahab and Azzam[1] have studied unsteady three dimensional combined heat and mass transfer for convective flow over a stretching surface with time dependent chemical reaction. Sahin[13] studied oscillatory three dimensional flow and heat and mass transfer through a porous medium in presence of periodic suction. Singh and Gupta[14]have studied MHD free convective flow of a viscous fluid through a porous medium bounded by an oscillating porous plate in slip flow regime with mass transfer.Radiative heat transfer flow is very important in manufacturing industries for the design of reliable equipments, nuclear plants, gas turbines and various propulsion devices for aircraft, missiles, satellites and space vehicles. Similarly, the effects of thermal radiation on the forced and free convection flows are important in the content of space technology and processes involving high temperature. Based on these applications, England and Emery[6] studied the thermal radiation effect of an optically thin gray gas bounded by a stationary vertical plate. Hayat et al.[8] studied the effect of thermal radiation on the flow of a second grade fluid. Raptis et al.[11] studied the effects of radiation in an optically thin gray gas flowing past a vertical infinite plate in presence of a magnetic field. Cookey et al.[5] studied the influence of viscous dissipation and radiation on unsteady MHD free convection flow past an infinite heated vertical plate in a porous medium with time dependent suction. Ghosh and B’eg[7] have done a theoretical analysis of radiative effects on transient free convection heat transfer past a hot vertical surface in porous media.Flows through porous medium are of principle interest because these are quite prevalent in nature. Such flows have many engineering applications, viz., in the fields of Petroleum technology to study the movement of natural gas, oil and water through the oil reservoirs, in chemical Engineering for filtration and purification process, and seepage of water in river beds to study the underground water resources. In view of these applications, different scholars have made a series of investigation where porous medium is either bounded by horizontal or vertical surfaces. Chaudhary and Sharma[4] studied the three dimensional unsteady convection and mass transfer flow through a porous medium. Ahmed and Ahmed[3] studied oscillatory three dimensional flow through a porous medium with viscous dissipative heat. Singh and Sharma[15] studied three dimensional free convective flow and heat transfer through porous medium with periodic permeability. Sahin[12] studied transient three dimensional flows through a porous medium with transverse permeability oscillating with time.In a geothermal region a situation may arise when velocity slip at the boundary may occur. In many practical applications, the particle adjacent to the solid surface no longer takes the velocity of the surface, it has a finite tangential velocity and it slips along the surface. The flow regime is called the slip flow regime. Jain and Sharma[10] and Jain and Gupta[9] have studied three dimensional coutte flow with slip boundary conditions and suction velocity vary sinusoidaly.Thus, the aim of this paper is to study an unsteady three dimensional free convective heat and mass transfer flow through a porous medium with constant heat and mass flux and periodic permeability in slip flow regime. Hence, numerical calculations up to the fourth level of truncation were carried out to investigate the effects of permeability parameter (K), velocity slip parameter (h1), thermal Grashof number (Gr), mass Grashof number (Gc), suction parameter (λ), Prandtl number (Pr) etc., on velocity (u), cross flow velocity (w), temperature (θ), concentration (C), skin friction (τx) and the rate of heat transfer (Nu) of such a flow. Results are illustrated graphically. The analysis of the result shows that our velocity increases as the permeability rises and also we notice that skin friction is higher in air (Pr=0.71) as compared to water (Pr=7).
2. Formulation of the Problem
- Here, we introduce a co-ordinate system with wall lying vertically on x-z plane, such that x-axis is oriented in the direction of the buoyancy force and y-axis is perpendicular to the plane of the wall and directed into the fluid. The permeability of the porous medium is assumed to be
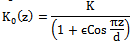 whereK0 = mean permeability of the medium.d = wave length of permeability distribution. = amplitude of permeability variation.Due to such a permeability variation, the problem is three dimensional. Denoting the velocity component u, v, w in the x, y, z directions respectively and the temperature by θ. The concentration level of the foreign mass present has been considered to be very small. The plate is subjected to a constant heat and mass flux.Under these conditions and using the Boussinesq approximation, governing equations of the flow are given by:
whereK0 = mean permeability of the medium.d = wave length of permeability distribution. = amplitude of permeability variation.Due to such a permeability variation, the problem is three dimensional. Denoting the velocity component u, v, w in the x, y, z directions respectively and the temperature by θ. The concentration level of the foreign mass present has been considered to be very small. The plate is subjected to a constant heat and mass flux.Under these conditions and using the Boussinesq approximation, governing equations of the flow are given by: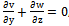 | (1) |
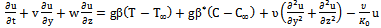 | (2) |
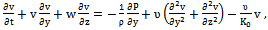 | (3) |
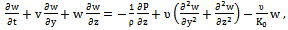 | (4) |
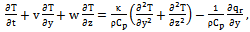 | (5) |
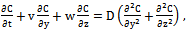 | (6) |
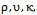 Cp and D are density, kinematic viscosity, thermal conductivity, specific heat at constant pressure and diffusion coefficient respectively.The boundary conditions are given by:where q and m are uniform heat and concentration flux at the plate respectively. The local radiant for the case of optically thin gray gas is expressed by:
Cp and D are density, kinematic viscosity, thermal conductivity, specific heat at constant pressure and diffusion coefficient respectively.The boundary conditions are given by:where q and m are uniform heat and concentration flux at the plate respectively. The local radiant for the case of optically thin gray gas is expressed by: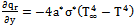 | (8) |
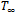 and neglecting the higher order, thus:
and neglecting the higher order, thus: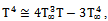 | (9) |
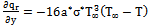 | (10) |
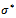 is Stephen-Boltzmann constant and
is Stephen-Boltzmann constant and 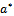 is absorption coefficient.On introducing the following non-dimensional quantities:
is absorption coefficient.On introducing the following non-dimensional quantities: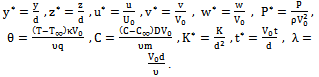 Equations (2) to (6), using (10), in non-dimensional form after dropping the asterik are:
Equations (2) to (6), using (10), in non-dimensional form after dropping the asterik are: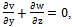 | (11) |
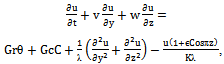 | (12) |
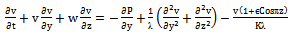 | (13) |
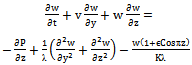 | (14) |
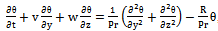 | (15) |
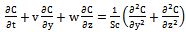 | (16) |
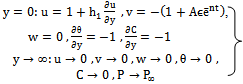 | (17) |
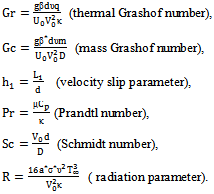
3. Solution of the Problem
- Since the amplitude of the suction velocity
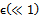 is very small, we now assume the solution of the following form:
is very small, we now assume the solution of the following form: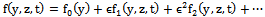 | (18) |
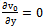 | (19) |
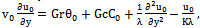 | (20) |
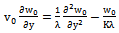 | (21) |
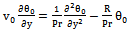 | (22) |
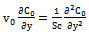 | (23) |
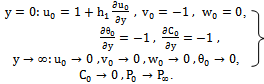 | (24) |
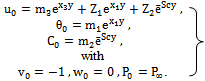 | (25) |
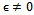 ,substituting equation (18) in (11) to (16) and comparing the coefficients of identical powers of
,substituting equation (18) in (11) to (16) and comparing the coefficients of identical powers of 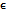 , neglecting those of
, neglecting those of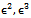 ..etc, the following first order equations are obtained:
..etc, the following first order equations are obtained: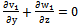 | (26) |
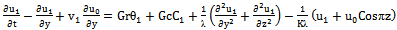 | (27) |
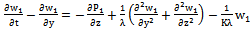 | (29) |
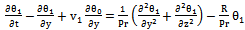 | (30) |
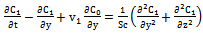 | (31) |
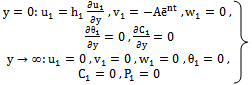 | (32) |
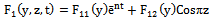 | (33) |
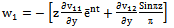 | (34) |
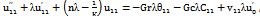 | (35) |
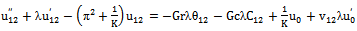 | (36) |
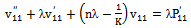 | (37) |
 | (38) |
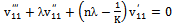 | (39) |
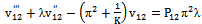 | (40) |
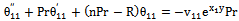 | (41) |
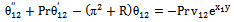 | (42) |
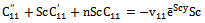 | (43) |
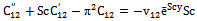 | (44) |
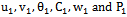 are obtained as:
are obtained as: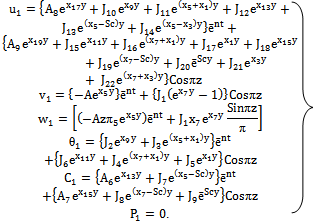 | (46) |
4. Skin Friction
- Once the velocity component u is known, we can now calculate an important parameter dimensionless skin friction in the main flow and the transverse direction as:
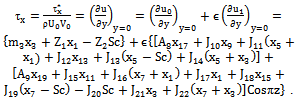
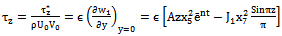
5. Nusselt Number
- Another important physical parameter of interest viz. Nusselt number is given by:
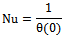
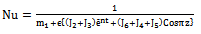 where
where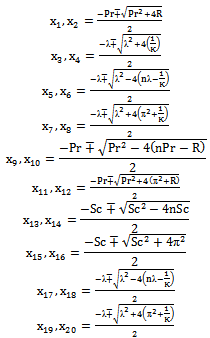

6. Results and Discussions
- In order to point out the effects of different parameters on velocity (u), cross flow velocity (w), temperature (θ), concentration (C), skin friction (τx) and the rate of heat transfer (Nu) the following discussions are set out. Numerical calculations are carried out for different values of the permeability parameter(K), velocity slip parameter(h1), thermal Grashof number(Gr), mass Grashof number(Gc), suction parameter(λ), Prandtl number(Pr) and Schmidt number(Sc). The values of Prandtl number(Pr) are chosen to be 0.71 and 7 which approximately represent air and water respectively at 20℃. The values of Gr and Gc are chosen arbitrarily. We fix ϵ=0.05, n=0.1 and t=1, A=0.5 (except concentration).In figure 1, velocity distribution is plotted against y, fixing z=0.25, and R=0.2. It is evident from this figure that the velocity increases with increase in K, h1, λ and Gr. Interpreting physically, increase in the permeability parameter(K) increases the flow which leads to increase in velocity. We further notice that increasing Gc decreases the velocity on the plate but rises as we move away from the plate. We have specially observed the result in air(Pr=0.71) and water(Pr=7) choosing values of Sc as 0.61 and 1.002. We observe that for same Sc velocity is higher in air than in water, this is due to the fact that air is lighter than water. Also we notice that for both the basic fluids air and water velocity is higher for Sc=0.61 and lower for Sc=1.002. We have made observations for K=
 viz. free flow and notice that the velocity increases. When K=
viz. free flow and notice that the velocity increases. When K= and h1=0(no slip), the velocity drops in comparison with h1≠0 and when K=
and h1=0(no slip), the velocity drops in comparison with h1≠0 and when K= , h1=0 and λ=0(suction parameter is zero), velocity decreases very slightly as we move away from the plate.The cross flow velocity component (w) is due to transverse suction velocity distribution applied through the plate at rest. This secondary flow component is shown in figure 2, plotted against y and taking water as the fluid (Pr=7). We notice that w increases on increasing z and as λ increases, w decreases near the plate but increases as we move away from the plate.
, h1=0 and λ=0(suction parameter is zero), velocity decreases very slightly as we move away from the plate.The cross flow velocity component (w) is due to transverse suction velocity distribution applied through the plate at rest. This secondary flow component is shown in figure 2, plotted against y and taking water as the fluid (Pr=7). We notice that w increases on increasing z and as λ increases, w decreases near the plate but increases as we move away from the plate.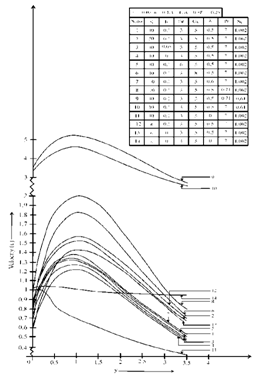 | Figure 1. Velocity profiles plotted against y for different values of K, h, Gr, Gc, λ, Pr, and Sc |
 | Figure 2. Cross flow velocity profiles in water against y for different values of λ and z |
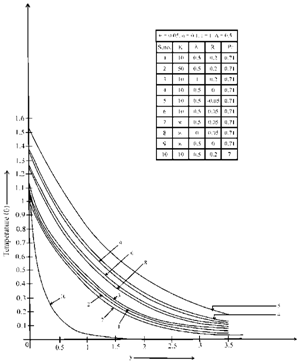 | Figure 3. Temperature profiles plotted against for different values of K, λ, R and Pr |
 temperature dips this is due to the fact that the distance between the particles increases and hence the temperature drops. For K=
temperature dips this is due to the fact that the distance between the particles increases and hence the temperature drops. For K= , temperature rises in both the cases when λ=0 and R=0. Further we see that temperature is lower in water (Pr=7) as compared in air (Pr=0.71).In figure 4, Concentration profiles are plotted against y, fixing z=0.25. We observe that concentration decreases on increasing K, Sc and A whereas it increases on increasing λ. Observations made for free flow K=
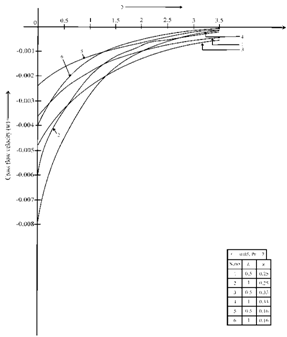
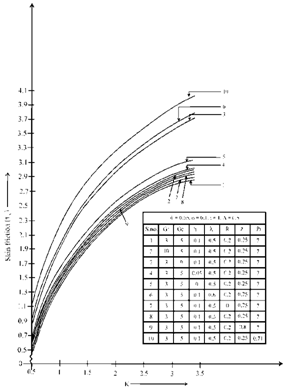
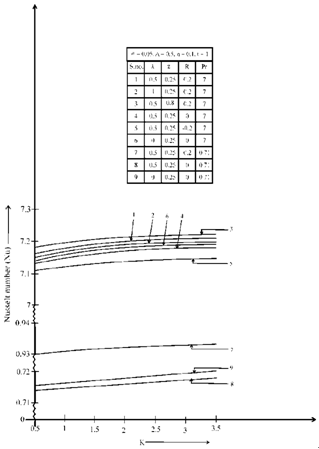
, temperature rises in both the cases when λ=0 and R=0. Further we see that temperature is lower in water (Pr=7) as compared in air (Pr=0.71).In figure 4, Concentration profiles are plotted against y, fixing z=0.25. We observe that concentration decreases on increasing K, Sc and A whereas it increases on increasing λ. Observations made for free flow K= and λ=0, shows that the concentration decreases. Interpreting physically, we can say that when we increase the permeability parameter (K) it increases the gap between the particles of the fluid leading to decrease in concentration.Skin friction in main flow direction is plotted against K in figure 5. We observe that skin friction increases on increasing Gr, Gc, λ and z, on the other hand skin friction increases on decreasing h1 and R. For negative of radiation (absorption) skin friction increases. Increase in skin friction due to Gc is more than that due to Gr. Also we specially observe that skin friction is higher in air (Pr=0.71) than in water (Pr=7), this is due the fact that velocity is higher in air than in water.In figure 6, Nusselt number profiles are plotted against K. We notice that for water (Pr=7), the rate of heat transfer decreases on increasing λ and same happens on decreasing z. Further we observe that for both the basic fluids air (Pr=0.71) and water (Pr=7), the rate of heat transfer decreases on decreasing R. Also we specially observe that when both λ=0 and R=0 the rate of heat transfer falls. It is generally observed that the rate of heat transfer is higher in water than in air.
and λ=0, shows that the concentration decreases. Interpreting physically, we can say that when we increase the permeability parameter (K) it increases the gap between the particles of the fluid leading to decrease in concentration.Skin friction in main flow direction is plotted against K in figure 5. We observe that skin friction increases on increasing Gr, Gc, λ and z, on the other hand skin friction increases on decreasing h1 and R. For negative of radiation (absorption) skin friction increases. Increase in skin friction due to Gc is more than that due to Gr. Also we specially observe that skin friction is higher in air (Pr=0.71) than in water (Pr=7), this is due the fact that velocity is higher in air than in water.In figure 6, Nusselt number profiles are plotted against K. We notice that for water (Pr=7), the rate of heat transfer decreases on increasing λ and same happens on decreasing z. Further we observe that for both the basic fluids air (Pr=0.71) and water (Pr=7), the rate of heat transfer decreases on decreasing R. Also we specially observe that when both λ=0 and R=0 the rate of heat transfer falls. It is generally observed that the rate of heat transfer is higher in water than in air.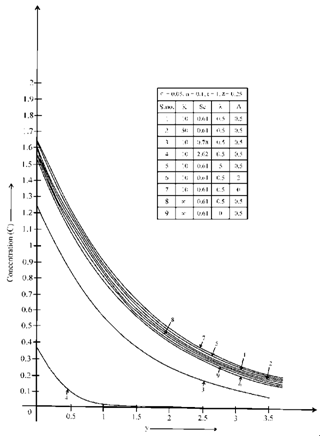 | Figure 4. Concentration profiles plotted against for different values of K, Sc, λ and A |
 | Figure 5. Skin friction plotted against K for different values of Gr, Gc, h1, λ, R, Z, Pr |
 | Figure 6. Nusselt number plotted against K for different values of λ, z, R, Pr |
ACKNOWLEDGEMENTS
- Authors are thankful to the learned referee for the valuable suggestions to improve the worth of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML