G. M. Moatimid, M. H. M. Moussa, Rehab M. El-Shiekh, A. A. El-Satar
Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt
Correspondence to: A. A. El-Satar, Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
By using symbolic computation, we apply Auxiliary equation method to construct exact solutions of Non-Linear Klein-Gordon equation. We show that Auxiliary equation method provides a powerful mathematical tool for solving nonlinear evolution equations in mathematical physics.
Keywords:
Traveling Wave, Exact Solutions And Auxiliary Equation
1. Introduction
The investigation of the travelling wave solutions for non-linear partial differential equations plays an important role in the study of non-linear physical phenomena. Non-linear wave phenomena appears in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics and geochemistry. Non-linear wave phenomena of dispersion, dissipation, diffusion, reaction and convection are very important in non-linear wave equations. In recent years, new exact solutions may help to find new phenomena. A variety of powerful methods, such as inverse scattering method[1, 2], bilinear transformation[3], the tanh-sech method[4-6], extended tanh method[7,8], sine-cosine method[9,10], homogeneous balance method[11], Exp-function method[12,13], improved tanh-function method[14] and Auxiliary equation method[15] were used to develop non-linear dispersive and dissipative problems.
2. Auxiliary Equation Method
Consider a given nonlinear wave equation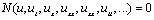 | (2.1) |
we seek its wave solutions.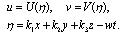 | (2.2) |
Consequently, (1.1) is reduced to the ordinary differential equation (ODE):Auxiliary equation method is based on the assumption that the travelling wave solutions can be expressed in the following form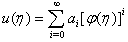 | (2.4) |
where φ(η) satisfies Auxiliary equation method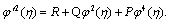 | (2.5) |
3. Non-Linear Klein-Gordon Equation
We study the following well-known the nonlinear Klein-Gordon equation: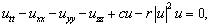 | (3.1) |
for 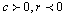 .To Higgs equation and for c = 0, it assumes the form of Yang-Milles equation. The Klein- Gordon equation has been studied in many literatures, e.g.,[16-18]. However, numerical treatment for Klein--Gordon equation is rarely reported (cf.[19-21]). Particularly,[20] concern with the decomposition method and difference method used in[21] nonlinear problems. We take u=U+i V, then by used he transformation (2.2) we get:
.To Higgs equation and for c = 0, it assumes the form of Yang-Milles equation. The Klein- Gordon equation has been studied in many literatures, e.g.,[16-18]. However, numerical treatment for Klein--Gordon equation is rarely reported (cf.[19-21]). Particularly,[20] concern with the decomposition method and difference method used in[21] nonlinear problems. We take u=U+i V, then by used he transformation (2.2) we get: 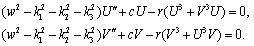 | (3.2) |
Now balancing U′′ with U³and V′′ with U³V gives M=1, N=1. Therefore we may choose: 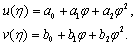 | (3.3) |
Substituting from equations (3.3) in equation (3.1), collect the coefficients of φ(η)i (i = 0, ..., 3) and equated them to zero we obtain the system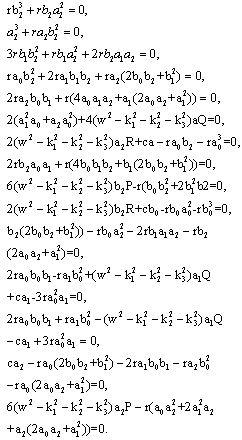 | (3.4) |
Solving the system of algebraic equations with the aid of Maple, in Eq.(3.3), we obtain the following results: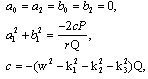 | (3.5) |
Substituting these results into (3.3) and with the aid of Appendix A, we obtain the following multiple soliton-like and triangular periodic solutions for (DSW) system: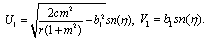 | (3.6) |
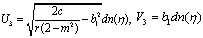 | (3.8) |
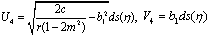 | (3.9) |
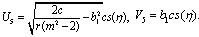 | (3.10) |
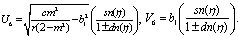 | (3.11) |
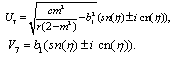 | (3.12) |
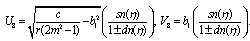 | (3.13) |
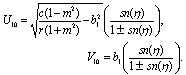 | (3.15) |
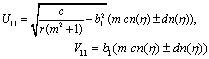 | (3.16) |
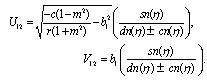 | (3.17) |
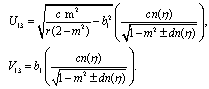 | (3.18) |
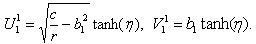 | (3.19) |
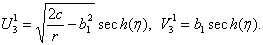 | (3.20) |
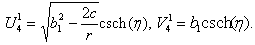 | (3.21) |
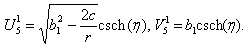 | (3.22) |
Some trigonometric-function solutions of Eq. (3.1) can be obtained in the limited case when the modulus m → 0(see Appendix B). For example,
4. Conclusions
In this study, we have applied Auxiliary equation method to obtain the generalized solitary wave solutions of Non-Linear Klein-Gordon equation. As we can see in the example of (K. G.) equation, the main advantage of this method over the other methods is that it can be applied to a wide class of nonlinear evolution equations including those in which the odd and even-order derivative terms are coexist. It may be concluded that, Auxiliary equation method can be easily extended to all kinds of nonlinear equations.
Appendix A



References
| [1] | MJ. Ablowitz, H. Segur. : ; 1981 . |
| [2] | VO. Vakhnenk , EJ. Parke , AJ. Morrison. Chaos, Solitons & Fractals 2003;17(4):683 92. |
| [3] | R. Hirota. Springer;1980.p.115775. |
| [4] | W. Malfliet. Am J. Phys 1992;60:650--- 4. |
| [5] | AM.Wazwaz. Math Comput Modelling 2004;40:499 508. |
| [6] | E.Fan, H.Zhang. Phys. Lett 1998;246:403-6. |
| [7] | F.Caloger, A.Degasperis. Nuovo Cimento B 32, 201, (1976). |
| [8] | JH. He, MA. Abdou. Chaos, Solitons & Fractals 2007;34:1421 9. |
| [9] | O. Bogoyavlenskii. Usp. Mat. Nauk. 45, 17, (1990). |
| [10] | Chen Huai-Tang, Zhang Hong-Qing. Chaos, Solitons and Fractals 20 (2004) 765—769. |
| [11] | A. A. Halim, S. B. Leble. Chaos, Solitons and Fractals 19 (2004) 99-108. |
| [12] | A. A. Halim, S. B. Leble. Chaos, Solitons and Fractals 19 (2004) 99-108. |
| [13] | JH. He, MA. . Chaos, Solitons & Fractals 2007;34:14219. |
| [14] | Chen Huai-Tang, Zhang Hong-Qing,. Chaos, Solitons and Fractals 20 (2004) 765.769. |
| [15] | P.G. Kevrekidis, V.V. Konotop, Math. Comput. Simulat. 62 (2003) 79.89. |
| [16] | P.G. Kevrekidis, V.V. Konotop, Math. Comput. Simulat. 62 (2003) 79.89. |
| [17] | S. Nakagiri, J. Ha, Nonlinear Anal. 47 (2000) 89.100. |
| [18] | R. Temam. Applied Math. Sci., 68, Springer-Verlag, 1988. |
| [19] | H. Fusaoka, J. Phys. Soc., Japan 59 (2) (1990) 455.463. |
| [20] | D. Kaya, S.M. El-Sayed, Applied Mathematics and Computation, (2003) in press. |
| [21] | I.J. Lee, J. Korean Math. Soc. 32 (3) (1995) 541.551. |
| [22] | M.H.M. Moussa, Rehab M. El-Shiekh. Intern. J. Nonlinear Sci. Vol.10(2010)No. 1, pp70-76. |

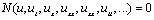
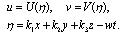
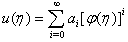
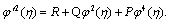
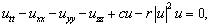
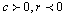 .To Higgs equation and for c = 0, it assumes the form of Yang-Milles equation. The Klein- Gordon equation has been studied in many literatures, e.g.,[16-18]. However, numerical treatment for Klein--Gordon equation is rarely reported (cf.[19-21]). Particularly,[20] concern with the decomposition method and difference method used in[21] nonlinear problems. We take u=U+i V, then by used he transformation (2.2) we get:
.To Higgs equation and for c = 0, it assumes the form of Yang-Milles equation. The Klein- Gordon equation has been studied in many literatures, e.g.,[16-18]. However, numerical treatment for Klein--Gordon equation is rarely reported (cf.[19-21]). Particularly,[20] concern with the decomposition method and difference method used in[21] nonlinear problems. We take u=U+i V, then by used he transformation (2.2) we get: 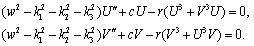
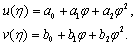
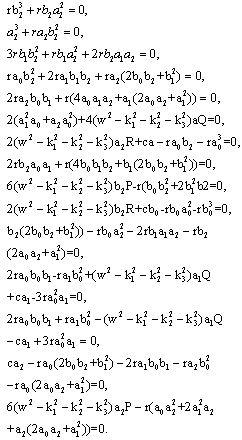
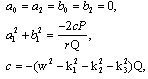
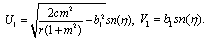
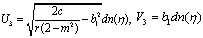
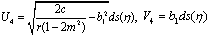
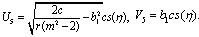
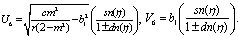
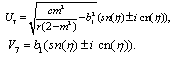
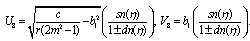
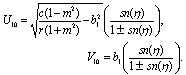
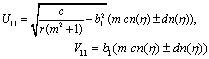
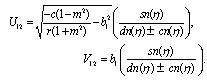
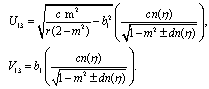
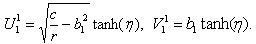
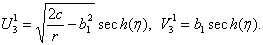
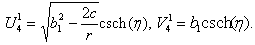
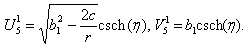



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML