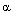-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(2): 28-33
doi: 10.5923/j.am.20120202.06
Self-Similar Flow under the Action of Monochromatic Radiation Behind a Cylindrical MHD Shock in a Non-Ideal Gas
J. P. Vishwakarma , Vijay Kumar Pandey
Dept. of Mathematics & Statistics, D.D.U. Gorakhpur University Gorakhpur, 273009, India
Correspondence to: J. P. Vishwakarma , Dept. of Mathematics & Statistics, D.D.U. Gorakhpur University Gorakhpur, 273009, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Similarity solutions are obtained for one-dimensional flow under the action of monochromatic radiation behind a cylindrical magnetogasdynamic shock wave propagating in a non-ideal gas in presence of an axial magnetic field. The initial density of the medium and initial magnetic field are assumed to be constant. It is investigated that the presence of the magnetic field or the non-idealness of the gas decays the shock wave, and when the initial magnetic field is strong the non-idealness of the gas affects the velocity and pressure profiles significantly. Also, it is observed that the flow-variables behind the shock are affected significantly, by an increase in the parameter of radiation, when the initial magnetic field is strong. It is, therefore, inferred that the effect of the non-idealness of the gas and of the monochromatic radiation on the shock propagation become more significant when the strength of the initial magnetic field is increased.
Keywords: Shock Wave, Self-similar Flow, Non-ideal Gas, Magnetohydrodynamics, Monochromatic Radiation
Article Outline
1. Introduction
- In gasdynamics, if the effects of radiation are taken into account, the basic non-linear equations are of a very complicated form and therefore it is essential to establish approximations which are physically accurate and can afford considerable simplifications. The problem of the interaction of radiation with gasdynamics has been studied by many authors by using the method of self-similarity developed by Sedov[1]. Marshak[2] studied the effect of radiation on the shock propagation by introducing the radiation diffusion approximation. He solved both the cases of constant density and constant pressure fields without invoking conditions of self-similarity. Using the same mode of radiation, Elliott[3] discussed the conditions leading to self-similarity with a specified functional form of the mean free-path of radiation and obtained a solution for self-similar explosions. Wang[4], Helliwell[5] and Nicastro[6] treated the problems of radiating walls, either stationary or moving, generating shock at the head of self-similar flow-fields. Assuming the shock to be isothermal and transparent the self-similar solution of the central explosions in stars has been obtained by Ray and Bhowmick[7] including the effects of radiation.The self-similar solutions have been used by Khudyakov [8] to discuss the problem of the motion of a gas under the action of monochromatic radiation. Khudyakov[8] has considered that a homogeneous gas at rest occupies a half-space bounded by a fixed plane wall and assumed that a radiation flux moves through the gas in the direction of the wall with a constant intensity
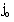 per unit area. From the instant of arrival of the radiation at the wall a shock wave is assumed to propagate out from the wall in the direction opposite to the radiation flux. The radiation flux is absorbed in the zone between the shock wave and the wall, and it is not absorbed in the undisturbed medium. It is also assumed that the gas itself does not radiate. Zheltukhin[9] has developed a family of exact solutions of one dimensional motion (plane, cylindrical or spherical symmetry) of a gas taking into account of the absorption of monochromatic radiation. Nath and Takhar[10] and Nath[11] have studied the propagation of cylindrical shock waves in a gas under the action of monochromatic radiation when the medium is rotating or non-rotating.Since at high temperatures that prevail in the problems associated with shock wave a gas is ionized, electromagnetic effects may also be significant. A complete analysis of such a problem should therefore consist of the study of the gasdynamic flow and the electromagnetic filed simultaneously. The study of the propagation of cylindrical shock waves in a conducting gas in presence of an axial or azimuthal magnetic field is relevant to the experiments on pinch effect, exploding wires, and so forth. This problem both in the uniform or non-uniform ideal gas was undertaken by many investigators, for example, Pai[12], Cole and Grefinger[13], Sakurai[14], Bhutani[15], Christer and Helliwell[16], Deb Ray[17] and Vishwakarma and Yadav[18]. Nath[19] and Shinde[20] have considered the effect of magnetic field on the propagation of cylindrical shock waves under the action of monochromatic radiation by using the method of self-similarity. In all of these works, the medium is assumed to be a gas obeying the equation of state of an ideal gas.Because of high pressure and density that generally occur behind a shock wave, produced by an explosion, the assumption that the gas is ideal is no more valid. The popular alternative to the ideal gas is a simplified van der Waals model. Roberts and Wu[21] and Wu and Roberts[22] adopted this model to discuss the shock wave theory of sonoluminescence. In the present work, we too adopt this as our model of a non-ideal gas to discover how deviations from the ideal gas can affect the self-similar solutions for the flow with monochromatic radiation behind a magnetogasdynamic cylindrical shock wave propagating in a non-ideal gas permeated by an axial magnetic field. The non-ideal gas is assumed to have infinite electrical conductivity and constant specific heats. The initial density of the medium and the initial magnetic field are assumed to be constant.Effects of a change in the strength of initial magnetic field, in the parameter of non-idealness of the gas and in the parameter of the flux of monochromatic radiation on the shock propagation are investigated. It is observed that the effects of non-idealness of the gas and the monochromatic radiation on the flow variables in the flow-field behind the shock are significant when the initial magnetic field is strong. The present work may be considered as an extension of the work of Nath[11] by taking the medium a non-ideal gas in place of an ideal gas.
per unit area. From the instant of arrival of the radiation at the wall a shock wave is assumed to propagate out from the wall in the direction opposite to the radiation flux. The radiation flux is absorbed in the zone between the shock wave and the wall, and it is not absorbed in the undisturbed medium. It is also assumed that the gas itself does not radiate. Zheltukhin[9] has developed a family of exact solutions of one dimensional motion (plane, cylindrical or spherical symmetry) of a gas taking into account of the absorption of monochromatic radiation. Nath and Takhar[10] and Nath[11] have studied the propagation of cylindrical shock waves in a gas under the action of monochromatic radiation when the medium is rotating or non-rotating.Since at high temperatures that prevail in the problems associated with shock wave a gas is ionized, electromagnetic effects may also be significant. A complete analysis of such a problem should therefore consist of the study of the gasdynamic flow and the electromagnetic filed simultaneously. The study of the propagation of cylindrical shock waves in a conducting gas in presence of an axial or azimuthal magnetic field is relevant to the experiments on pinch effect, exploding wires, and so forth. This problem both in the uniform or non-uniform ideal gas was undertaken by many investigators, for example, Pai[12], Cole and Grefinger[13], Sakurai[14], Bhutani[15], Christer and Helliwell[16], Deb Ray[17] and Vishwakarma and Yadav[18]. Nath[19] and Shinde[20] have considered the effect of magnetic field on the propagation of cylindrical shock waves under the action of monochromatic radiation by using the method of self-similarity. In all of these works, the medium is assumed to be a gas obeying the equation of state of an ideal gas.Because of high pressure and density that generally occur behind a shock wave, produced by an explosion, the assumption that the gas is ideal is no more valid. The popular alternative to the ideal gas is a simplified van der Waals model. Roberts and Wu[21] and Wu and Roberts[22] adopted this model to discuss the shock wave theory of sonoluminescence. In the present work, we too adopt this as our model of a non-ideal gas to discover how deviations from the ideal gas can affect the self-similar solutions for the flow with monochromatic radiation behind a magnetogasdynamic cylindrical shock wave propagating in a non-ideal gas permeated by an axial magnetic field. The non-ideal gas is assumed to have infinite electrical conductivity and constant specific heats. The initial density of the medium and the initial magnetic field are assumed to be constant.Effects of a change in the strength of initial magnetic field, in the parameter of non-idealness of the gas and in the parameter of the flux of monochromatic radiation on the shock propagation are investigated. It is observed that the effects of non-idealness of the gas and the monochromatic radiation on the flow variables in the flow-field behind the shock are significant when the initial magnetic field is strong. The present work may be considered as an extension of the work of Nath[11] by taking the medium a non-ideal gas in place of an ideal gas.2. Basic Equations and Boundary Conditions
- The fundamental equations for cylindrically symmetric motion of a non-ideal gas under the action of monochromatic radiation and axial magnetic field, neglecting heat-conduction, viscosity and radiation of the medium, may be written as (Khudyakov[8], Greifinger and Cole[13], Nath[19], Zedan[23])
 | (2.1) |
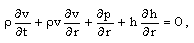 | (2.2) |
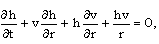 | (2.3) |
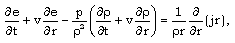 | (2.4) |
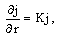 | (2.5) |
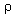 , v, p, h, e and j are the density, radial velocity, pressure, axial magnetic field, internal energy per unit mass and the monochromatic radiation at distance r from the axis at time t, and K is the absorption coefficient. Here the magnetic permeability is taken to be unity and the electrical conductivity to be infinite.Most of the phenomena associated with shock wave arise in extreme conditions under which the ideal gas is not a sufficiently accurate description. To discover how deviations from the ideal gas can affect the flow behind a shock wave, we adopt a simple model. We assume that the gas obeys a simplified van der waals equation of state of the form (Roberts and Wu[21], Wu and Roberts[22])
, v, p, h, e and j are the density, radial velocity, pressure, axial magnetic field, internal energy per unit mass and the monochromatic radiation at distance r from the axis at time t, and K is the absorption coefficient. Here the magnetic permeability is taken to be unity and the electrical conductivity to be infinite.Most of the phenomena associated with shock wave arise in extreme conditions under which the ideal gas is not a sufficiently accurate description. To discover how deviations from the ideal gas can affect the flow behind a shock wave, we adopt a simple model. We assume that the gas obeys a simplified van der waals equation of state of the form (Roberts and Wu[21], Wu and Roberts[22])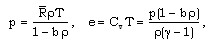 | (2.6) |
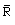 is the gas constant and
is the gas constant and 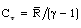 is the specific heat at constant volume and
is the specific heat at constant volume and 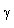 is the ratio of specific heats. The constant b is the “van der Waals excluded volume”, it places a limit,
is the ratio of specific heats. The constant b is the “van der Waals excluded volume”, it places a limit, 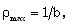 on the density of the gas.The absorption coefficient K is considered to vary as (Khudyakov[8], Nath[19], Nath and Takhar[10])
on the density of the gas.The absorption coefficient K is considered to vary as (Khudyakov[8], Nath[19], Nath and Takhar[10])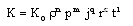 | (2.7) |
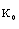 is a dimensional constant and the exponents n, m, q, s, l are rational numbers.A diverging cylindrical shock is assumed to be propagating in the perfectly conducting non-ideal gas with constant density, in presence of a uniform axial magnetic field. The jump conditions across the shock front which is transparent for the radiation flux, are as
is a dimensional constant and the exponents n, m, q, s, l are rational numbers.A diverging cylindrical shock is assumed to be propagating in the perfectly conducting non-ideal gas with constant density, in presence of a uniform axial magnetic field. The jump conditions across the shock front which is transparent for the radiation flux, are as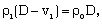 | (2.8) |
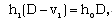 | (2.9) |
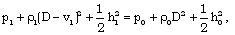 | (2.10) |
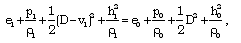 | (2.11) |
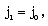 | (2.12) |
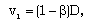 | (2.13) |
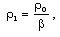 | (2.14) |
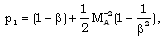 | (2.15) |
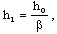 | (2.16) |
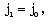 | (2.17) |
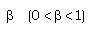 is obtained by the relation
is obtained by the relation 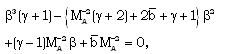 | (2.18) |
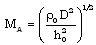 being the Alfven-Mach number and
being the Alfven-Mach number and 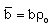 the parameter of non-idealness.
the parameter of non-idealness.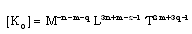 | (2.19) |
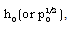
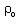 ,
, 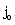 , and
, and 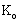 in which
in which 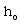 ,
,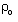 and
and 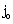 are dependent given by
are dependent given by 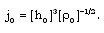 | (2.20) |
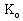 must be dependent on the dimensions of
must be dependent on the dimensions of 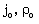 which is equivalent to
which is equivalent to 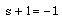 The self-similar independent dimensionless variable
The self-similar independent dimensionless variable 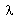 is taken in the form
is taken in the form 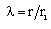 where
where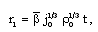 | (2.21) |
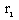 being the radius of the shock surface. The value of the constant
being the radius of the shock surface. The value of the constant 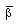 is so chosen that
is so chosen that 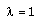 at the shock surface.
at the shock surface.3. Similarity Solutions
- We introduce the following similarity transformations to reduce the equation of motion into ordinary differential equations;
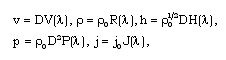 (3.1-3.5)where V, R, H, P and J are functions of the non-dimensional variable (similarity variable)
(3.1-3.5)where V, R, H, P and J are functions of the non-dimensional variable (similarity variable) 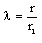 Using the transformations (3.1)-(3.5) the equations of motion take the form
Using the transformations (3.1)-(3.5) the equations of motion take the form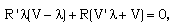 | (3.6) |
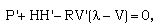 | (3.7) |
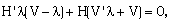 | (3.8) |
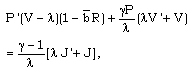 | (3.9) |
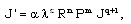 | (3.10) |
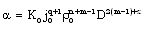 | (3.11) |
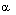 is taken as the parameter which characterizes the interaction between the gas and the incident radiation flux (Khudyakov[8], Nath[19], Nath and Takhar[10]).Solving equations (3.6)-(3.10) for
is taken as the parameter which characterizes the interaction between the gas and the incident radiation flux (Khudyakov[8], Nath[19], Nath and Takhar[10]).Solving equations (3.6)-(3.10) for 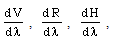
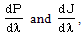 we have
we have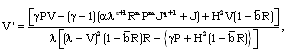 | (3.12) |
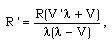 | (3.13) |
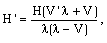 | (3.14) |
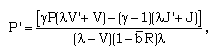 | (3.15) |
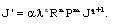 | (3.16) |
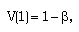 | (3.17) |
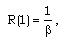 | (3.18) |
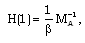 | (3.19) |
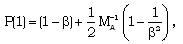 | (3.20) |
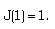 | (3.21) |
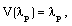 | (3.22) |
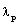 is the value of
is the value of 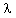 at the inner surface.For exhibiting the numerical solutions, it is convenient to write the flow variables in the non-dimensional form as
at the inner surface.For exhibiting the numerical solutions, it is convenient to write the flow variables in the non-dimensional form as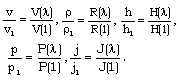 | (3.23) |
4. Results and Discussion
- The set of differential equations (3.12)-(3.16) are numerically integrated with the boundary conditions (3.17)-(3.21) to obtain the non-dimensional variables of the flow-field V, R, H, P and J against the similarity variable
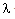 by using the Runge-Kutta method of order four, for the values (Khudyakov[8], Nath[19], Nath and Takhar[10], Ranga Rao and Purohit[24], Singh et. al[25], Vishwakarma and Singh[26])
by using the Runge-Kutta method of order four, for the values (Khudyakov[8], Nath[19], Nath and Takhar[10], Ranga Rao and Purohit[24], Singh et. al[25], Vishwakarma and Singh[26]) 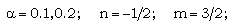
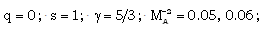
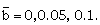 The case
The case 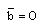 corresponds to the perfect gas case (Nath[19]). In figure 1 we have plotted the radial velocity
corresponds to the perfect gas case (Nath[19]). In figure 1 we have plotted the radial velocity 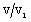 , in figure 2 the density
, in figure 2 the density 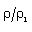 , in figure 3 the axial magnetic field
, in figure 3 the axial magnetic field 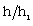 , in figure 4 the pressure
, in figure 4 the pressure 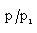 and in figure 5 the radiation flux
and in figure 5 the radiation flux 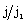 against the radial distance
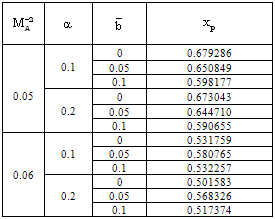
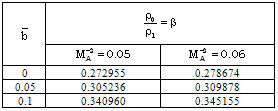
against the radial distance 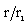 in flow-field between the inner expanding surface and the shock surface. Table 1 and table 2 show, respectively, the density ratio across the shock and the position of inner expanding surface for various values of the parameters
in flow-field between the inner expanding surface and the shock surface. Table 1 and table 2 show, respectively, the density ratio across the shock and the position of inner expanding surface for various values of the parameters 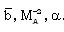 This solution shows that all the flow variables the velocity, the density, the pressure, the magnetic field and the radiation flux decrease from highest at the shock front to lowest at the inner expanding surface.From table 1 and table 2 and figure 1, figure 2, figure 3, figure 4 and figure 5 it is observed that the effects of an increase in the value of
This solution shows that all the flow variables the velocity, the density, the pressure, the magnetic field and the radiation flux decrease from highest at the shock front to lowest at the inner expanding surface.From table 1 and table 2 and figure 1, figure 2, figure 3, figure 4 and figure 5 it is observed that the effects of an increase in the value of 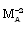 (i.e. the effects of an increase in the strength of ambient magnetic field) are(i) to decrease
(i.e. the effects of an increase in the strength of ambient magnetic field) are(i) to decrease 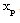 , i.e. to increase the distance of inner expanding surface from the shock front. Physically, it means that the gas behind the shock is less compressed, i.e. the shock strength is reduced;(ii) to decrease the value of
, i.e. to increase the distance of inner expanding surface from the shock front. Physically, it means that the gas behind the shock is less compressed, i.e. the shock strength is reduced;(ii) to decrease the value of 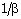 , i.e. to decrease the shock strength, which is the same as given in (i) above;(iii) to decrease the value of
, i.e. to decrease the shock strength, which is the same as given in (i) above;(iii) to decrease the value of 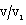 and
and  ; and to increase the value of
; and to increase the value of 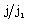 at any point in the flow-field behind the shock; and(iv) to enhance the effect of non-idealness of the gas on the profiles of
at any point in the flow-field behind the shock; and(iv) to enhance the effect of non-idealness of the gas on the profiles of 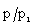 .Thus the presence of magnetic field decays the shock wave and enhances the effect of non-idealness of the gas on the pressure profiles behind the shock.The effects of an increase in the value of the parameter of the non-idealness of the gas
.Thus the presence of magnetic field decays the shock wave and enhances the effect of non-idealness of the gas on the pressure profiles behind the shock.The effects of an increase in the value of the parameter of the non-idealness of the gas 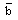 are(i) to increase the distance of the inner expanding surface from the shock front when
are(i) to increase the distance of the inner expanding surface from the shock front when 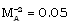 (see table 2); (ii) to decrease the value of
(see table 2); (ii) to decrease the value of 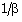 (table 1), i.e. to decrease the shock strength. Therefore the non-idealness of the gas has decaying effect on the shock wave;(iii) to decrease the value of
(table 1), i.e. to decrease the shock strength. Therefore the non-idealness of the gas has decaying effect on the shock wave;(iii) to decrease the value of 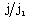 at any point in the flow-field behind the shock (see figure 5); and(iv) to change the values of
at any point in the flow-field behind the shock (see figure 5); and(iv) to change the values of 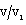 and
and 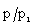 significantly at any point in the flow-field behind the shock when the magnetic field is strong (
significantly at any point in the flow-field behind the shock when the magnetic field is strong (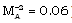 ).Thus the non-idealness of the gas decays the shock wave, and affects the velocity and pressure profiles significantly when the initial magnetic field is strong.Effects of an increase in the radiation parameter
).Thus the non-idealness of the gas decays the shock wave, and affects the velocity and pressure profiles significantly when the initial magnetic field is strong.Effects of an increase in the radiation parameter 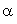 are(i) to decrease
are(i) to decrease 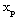 (table 2), i.e. to decrease the shock strength; and(ii) to decrease
(table 2), i.e. to decrease the shock strength; and(ii) to decrease 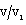
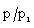 ,
, 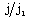 at any point in the flow-field behind the shock. This decrease in these flow-variables are enhanced when the initial magnetic field is strong (
at any point in the flow-field behind the shock. This decrease in these flow-variables are enhanced when the initial magnetic field is strong (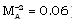 ).The above effects show that the monochromatic radiation is more absorbed by the gas in the flow-field behind the shock by an increase in the parameter
).The above effects show that the monochromatic radiation is more absorbed by the gas in the flow-field behind the shock by an increase in the parameter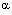 .
.
|
|
5. Conclusions
- The present work investigates the self-similar flow of a non-ideal gas under the action of monochromatic radiation behind a cylindrical shock wave in presence of a uniform axial magnetic field. The density of the ambient medium is also uniform. On the basis of this work, one may draw the following conclusions:(i) The presence of magnetic field decays the shock wave and enhances the effect of non-idealness of the gas on the pressure profiles behind the shock.(ii) The non-idealness of the gas decays the shock wave, and affects the velocity and pressure profiles significantly when the initial magnetic field is strong.(iii) An increase in
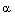 decreases the shock strength and the fluid velocity, the pressure and the radiation flux at any point in the flow-field behind the shock, and these behavior of the flow-variables show that the monochromatic radiation is more absorbed. These effects are significant when the initial magnetic field is strong.Thus it is inferred that the effect of the non-idealness of the gas and of the monochromatic radiation on the shock propagation become more significant when the strength of the initial magnetic field is increased.
decreases the shock strength and the fluid velocity, the pressure and the radiation flux at any point in the flow-field behind the shock, and these behavior of the flow-variables show that the monochromatic radiation is more absorbed. These effects are significant when the initial magnetic field is strong.Thus it is inferred that the effect of the non-idealness of the gas and of the monochromatic radiation on the shock propagation become more significant when the strength of the initial magnetic field is increased. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
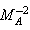 , parameter of non-idealness of the gas
, parameter of non-idealness of the gas 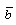 and parameter of radiation α
and parameter of radiation α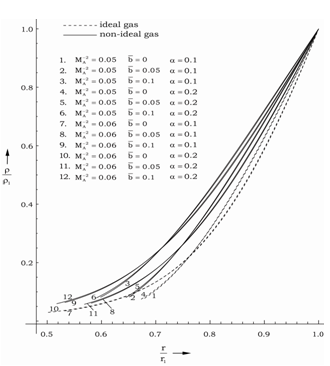
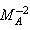 , parameter of non-idealness of the gas
, parameter of non-idealness of the gas 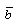 and parameter of radiation α
and parameter of radiation α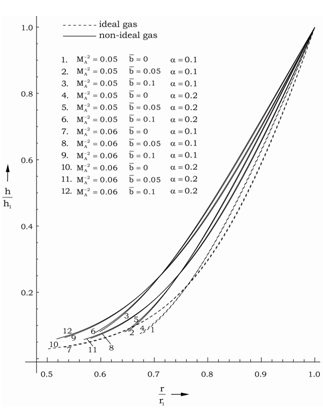
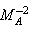 , parameter of non-idealness of the gas
, parameter of non-idealness of the gas 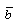 and parameter of radiation α
and parameter of radiation α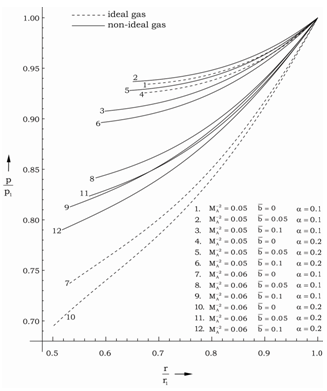
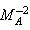 , parameter of non-idealness of the gas
, parameter of non-idealness of the gas 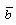 and parameter of radiation α
and parameter of radiation α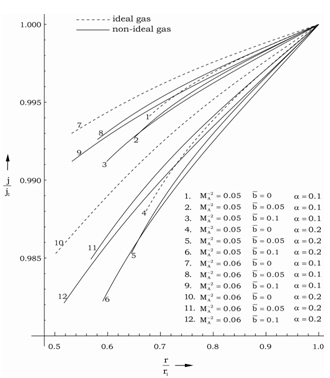
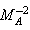 , parameter of non-idealness of the gas
, parameter of non-idealness of the gas 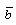 and parameter of radiation α
and parameter of radiation α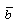 and
and 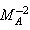
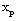 for
for 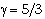 and various values of
and various values of 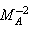 ,
, 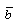 and
and