-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2012; 2(2): 21-27
doi: 10.5923/j.am.20120202.05
SOR- Steffensen-Newton Method to Solve Systems of Nonlinear Equations
M. T. Darvishi , Norollah Darvishi
Department of Mathematics, Razi University, Kermanshah, 67149, Iran
Correspondence to: M. T. Darvishi , Department of Mathematics, Razi University, Kermanshah, 67149, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we present SOR-Steffensen-Newton (SOR-SN) algorithm to solve systems of nonlinear equations. We study the convergence of the method. The computational aspects of the method is also studied using some numerical experiment. In comparison of new method with SOR-Newton, SOR-Steffensen and SOR-Secant methods, our method are better in CPU time and number of iterations.
Keywords: Nonlinear System, SOR-Newton Method, SOR-Steffensen Method, SOR-Secant Method, CPU Time
Article Outline
1. Introduction
- There are cases where thousands of nonlinear equations depending on some independent variables must be solved effectively. Consider the nonlinear system
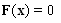 | (1) |
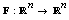 , that is, a system with
, that is, a system with 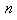 equations and
equations and 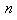 unknowns. Finding roots of systems of nonlinear equations efficiently is of major importance and has widespread applications in numerical and applied mathematics. There are many approaches to solve (1). The second order Newton's method is one of the most common iterative methods adopted for finding approximate solutions of nonlinear system (1) (for more details see[1]). The Newton's method to solve (1) is an important and basic method which converges quadratically. Recently, some third and fourth order iterative methods have been proposed and analyzed for solving systems of nonlinear equations that improve some classical methods such as the Newton's method and Chebyshev-Halley methods. It has been demonstrated that the methods are efficient, and can compete with Newton's method, for more details see[2-10]. To solve system (1), Darvishi and Barati[11-13] presented some high order iterative methods, free from second order derivative of function
unknowns. Finding roots of systems of nonlinear equations efficiently is of major importance and has widespread applications in numerical and applied mathematics. There are many approaches to solve (1). The second order Newton's method is one of the most common iterative methods adopted for finding approximate solutions of nonlinear system (1) (for more details see[1]). The Newton's method to solve (1) is an important and basic method which converges quadratically. Recently, some third and fourth order iterative methods have been proposed and analyzed for solving systems of nonlinear equations that improve some classical methods such as the Newton's method and Chebyshev-Halley methods. It has been demonstrated that the methods are efficient, and can compete with Newton's method, for more details see[2-10]. To solve system (1), Darvishi and Barati[11-13] presented some high order iterative methods, free from second order derivative of function  . Darvishi[14,15] presented some multi-step iterative methods, free from second order derivative of function
. Darvishi[14,15] presented some multi-step iterative methods, free from second order derivative of function  . Frontini and Sormani[16] obtained a third-order method based on a quadrature formula to solve systems of nonlinear equations. Babajee et al.[17] proposed a fourth order iterative method to solve system (1).One-step SOR-Newton method to solve nonlinear system (1) which presented in[1] is as follows:
. Frontini and Sormani[16] obtained a third-order method based on a quadrature formula to solve systems of nonlinear equations. Babajee et al.[17] proposed a fourth order iterative method to solve system (1).One-step SOR-Newton method to solve nonlinear system (1) which presented in[1] is as follows: 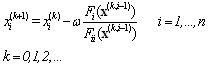 where
where 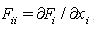 ,
, 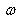 is the relaxation parameter in SOR method and
is the relaxation parameter in SOR method and 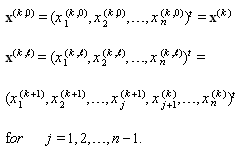 It is obvious that we have
It is obvious that we have 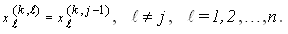 The aim of this paper is to introduce the SOR-SN algorothm. To achieve this, we follow the two-step Steffensen type method which presented by Ren et al[18]. They have presented a class of one-parameter Steffensen type methods with fourth-order convergence to solve nonlinear equations
The aim of this paper is to introduce the SOR-SN algorothm. To achieve this, we follow the two-step Steffensen type method which presented by Ren et al[18]. They have presented a class of one-parameter Steffensen type methods with fourth-order convergence to solve nonlinear equations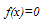 | (2) |
2. SOR- SN Algorithm
- In this section we introduce the SOR-SN algorithm, to solve systems of nonlinear equations. The SOR-SN method to solve
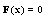 for
for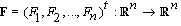 is defined by solving the following equation for
is defined by solving the following equation for 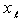
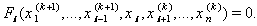 | (3) |
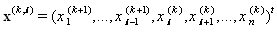 Then we obtain
Then we obtain 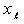 from (3) as follows
from (3) as follows 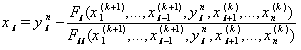 where
where 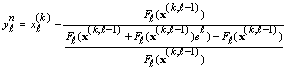 whereas
whereas 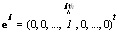 Finally, we set
Finally, we set 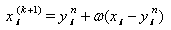 or
or 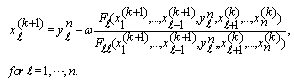 | (4) |
2.1. Convergence Analysis
- In this part, we state and prove convergence theorem for our SOR-SN method. The proof is similar to proof of convergency of SOR algorithm in[19]. First, to follow[19], we need some assumptions. These assumptions are as follows a) D is a convex set in
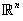 . b) For system
. b) For system 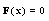 ,
, 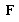 is gradient of
is gradient of 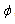 , namely,
, namely, 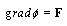 and function
and function 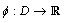 is strictly convex. c) On domain
is strictly convex. c) On domain 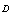 , function
, function 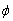 is twice continuously differentiable. d) Set
is twice continuously differentiable. d) Set 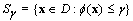 for some
for some 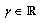 is nonempty and compact. Note that
is nonempty and compact. Note that 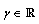 exists and set
exists and set 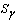 is nonempty and compact. e)
is nonempty and compact. e) 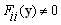 for
for 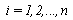 and
and 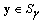 , unless
, unless 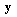 is the point at which
is the point at which 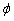 attains its minimum, where
attains its minimum, where 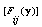 for
for 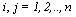 is Hessian matrix of
is Hessian matrix of 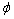 at
at 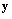 . Assumptions a) and b) show that the Hessian matrix of
. Assumptions a) and b) show that the Hessian matrix of 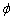 is positive definite. It is obvious that sets
is positive definite. It is obvious that sets 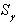 are convex for all
are convex for all 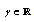 . Assumption d) shows that
. Assumption d) shows that 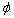 attains its minimum at some point
attains its minimum at some point 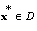 . If assumptions a), b) and c) hold and function
. If assumptions a), b) and c) hold and function 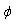 attains its minimum at some point
attains its minimum at some point 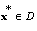 then assumption d) is nontrivially satisfied, that is, there exists
then assumption d) is nontrivially satisfied, that is, there exists 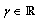 such that
such that 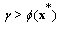 and
and 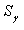 is compact also
is compact also 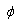 is a non-increasing function. From b) the minimum point
is a non-increasing function. From b) the minimum point 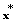 is unique. At last, a point
is unique. At last, a point 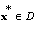 is the minimum point of function
is the minimum point of function 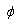 if and only if
if and only if 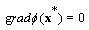 .Now, we can present the following theorem on convergency of SOR-SN method. Theorem 1. If sequence
.Now, we can present the following theorem on convergency of SOR-SN method. Theorem 1. If sequence 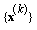 be generated by
be generated by 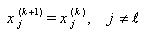 and
and 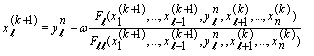 where
where 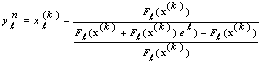 in fact, we have
in fact, we have 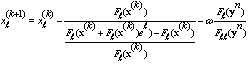 | (5) |
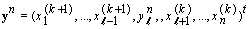 Also if
Also if 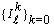 ,
,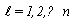 , be defined by
, be defined by 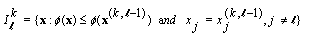 and
and 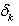 be defined by
be defined by 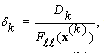 where
where 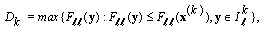 and for some
and for some 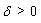 which satisfies in
which satisfies in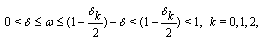 then for any
then for any 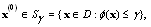 sequence
sequence 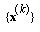 is well-defined and converges to
is well-defined and converges to 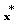 . Proof. We first prove that sequence
. Proof. We first prove that sequence 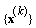 is well-defined. By consideration of structure of sets
is well-defined. By consideration of structure of sets 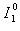 and
and 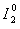 we have
we have 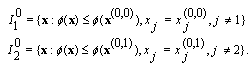 Note that we have
Note that we have 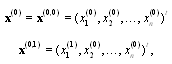 this shows that
this shows that 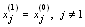 . But sequence
. But sequence  is non-increasing, thus
is non-increasing, thus 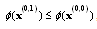 , from this we have
, from this we have 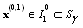 . In a similar manner and by mathematical induction we can prove that all terms of sequence
. In a similar manner and by mathematical induction we can prove that all terms of sequence 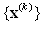 are contained in
are contained in 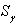 hence the sequence is well-defined. We now prove that
hence the sequence is well-defined. We now prove that 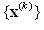 converges. By using Taylor's theorem on function
converges. By using Taylor's theorem on function 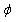 for
for 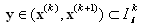 (where
(where 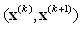 denotes the open line segment joining
denotes the open line segment joining 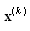 and
and 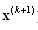 ) we have
) we have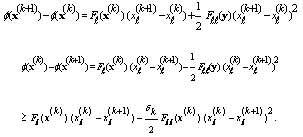 | (6) |
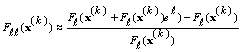 thus from (5) we have
thus from (5) we have 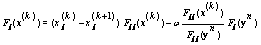 | (7) |
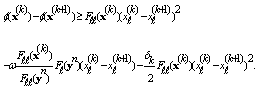 | (8) |
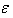 which satisfies in
which satisfies in 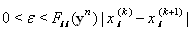 we have
we have 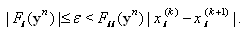 Consequently, from this and (8) we have
Consequently, from this and (8) we have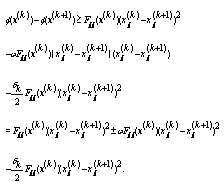 Thus
Thus 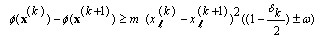 where
where 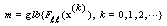 . Since the Hessian matrix of
. Since the Hessian matrix of 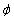 is positive semidefinite, hence
is positive semidefinite, hence 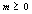 . We consider two cases for
. We consider two cases for 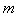 : Case 1.
: Case 1. 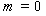 By assumption e) there exists some subsequence
By assumption e) there exists some subsequence 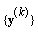 converges to
converges to 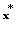 and we know that
and we know that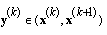 and as
and as 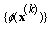 is a non-increasing sequence, we have
is a non-increasing sequence, we have 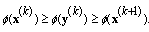 Therefore, by our assumption, as
Therefore, by our assumption, as 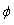 is a continuous function, we have
is a continuous function, we have 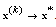 . Case 2.
. Case 2. 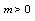 We know that
We know that 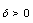 satisfies in
satisfies in 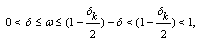 we consider two possible cases as follows: Case 1.
we consider two possible cases as follows: Case 1.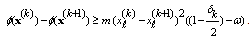 .We know that the sequence
.We know that the sequence 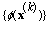 is non-increasing and bounded from below, hence it is a convergent sequence. Then
is non-increasing and bounded from below, hence it is a convergent sequence. Then 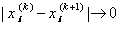 , we suppose that
, we suppose that 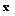 is a limit point of
is a limit point of 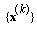 and we consider the following sets
and we consider the following sets 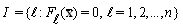 and
and 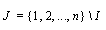 . From (7) we have
. From (7) we have 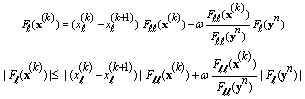 from the convergency of the Steffensen's method we have thus
from the convergency of the Steffensen's method we have thus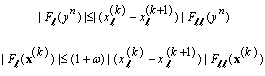 .As
.As  and
and 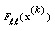 is bounded, hence we have
is bounded, hence we have 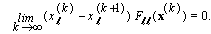 Thus
Thus 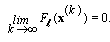 This shows that
This shows that 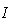 is a nonempty set. If
is a nonempty set. If 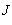 be an empty set, hence
be an empty set, hence 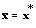 and as
and as 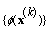 is a non-increasing sequence,
is a non-increasing sequence, 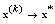 . Else if
. Else if 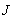 be a nonempty set, thus
be a nonempty set, thus 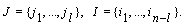 For
For 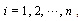 we define the following sets
we define the following sets 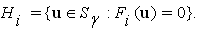 Clearly sets
Clearly sets 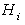 are closed and nonempty sets, because
are closed and nonempty sets, because 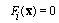 and
and 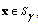 , hence
, hence 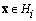 . Also we define
. Also we define 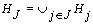 . Since
. Since 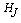 is a closed set then there exists
is a closed set then there exists 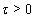 such that for
such that for 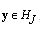 , we have
, we have 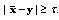 Remember that
Remember that 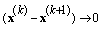 hence, there is an integer
hence, there is an integer 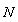 such that for
such that for 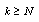 we have
we have 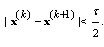 Let
Let 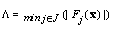 . From the continuity of
. From the continuity of 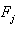 there exists
there exists 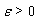 such that
such that 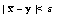 implies that
implies that 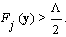 We define set
We define set 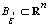 such that for all
such that for all 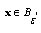 the following relations hold
the following relations hold 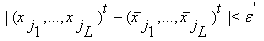 | (9) |
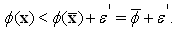 | (10) |
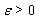 we may select
we may select 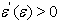 such that if
such that if 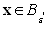 then
then 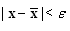 , otherwise for every sequence
, otherwise for every sequence 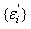 which reduces to zero, there exists
which reduces to zero, there exists 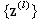 such that
such that 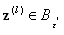 and
and 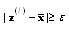 . All such
. All such 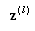 are contained in
are contained in 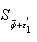 which is a compact set. This results that, there exists a limit point
which is a compact set. This results that, there exists a limit point 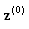 of
of 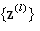 which is such that
which is such that 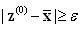 . We have from (9) that
. We have from (9) that 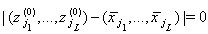 And also from (10) we have
And also from (10) we have 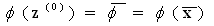 hence
hence 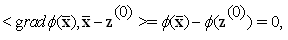 where
where 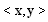 denotes the inner product of vectors
denotes the inner product of vectors 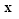 and
and 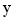 . This leads to a contradiction, because
. This leads to a contradiction, because 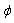 is a strictly convex function. Thus there exists
is a strictly convex function. Thus there exists 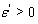 such that
such that 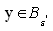 implies that
implies that 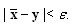 Also from
Also from 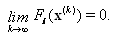 , there exists
, there exists 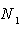 such that for
such that for 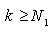 we have
we have 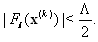 Also there exists
Also there exists 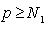 such that
such that 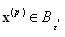 hence there is an
hence there is an 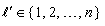 such that
such that 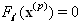 thus
thus 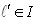 . If
. If 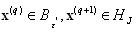 for
for 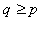 , then we have
, then we have 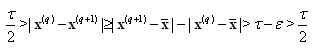 which is a contradiction. Hence
which is a contradiction. Hence 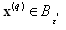 for
for 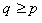 . This shows that for
. This shows that for 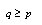 there is not any
there is not any 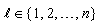 such that
such that 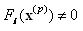 , therefore there is not any
, therefore there is not any 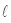 in
in 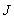 thus
thus 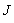 is an empty set, which is a contradiction. Thus
is an empty set, which is a contradiction. Thus 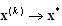 .Case 2.
.Case 2. 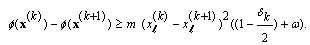 We can state a similar discussion for this case.
We can state a similar discussion for this case. 3. Numerical Results
- In this section we solve some nonlinear systems by SOR-SN method. We compare the CPU time and number of iterations of our method with SOR-Newton(SOR-N), SOR-Steffensen(SOR-St) and SOR-Secant(SOR-Se) methods. Numerical computations have been carried out in MATLAB. The stopping criteria is
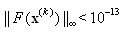 , where
, where 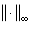 shows the Infinity norm.Note that in SOR-secant method we need to two initial guesses, namely
shows the Infinity norm.Note that in SOR-secant method we need to two initial guesses, namely 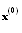 and
and 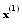 , while for another methods we only need to one initial guess. In the following parts, we present some examples to compare these methods: Example 1 . Consider the following nonlinear system
, while for another methods we only need to one initial guess. In the following parts, we present some examples to compare these methods: Example 1 . Consider the following nonlinear system 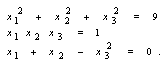 The exact solution of the above system is
The exact solution of the above system is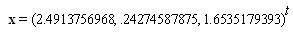 .For an initial guess we set
.For an initial guess we set 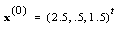 and
and 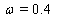 also for SOR-Secant method we set
also for SOR-Secant method we set 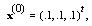
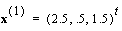 . The numerical results are given in Table 1.
. The numerical results are given in Table 1.
|
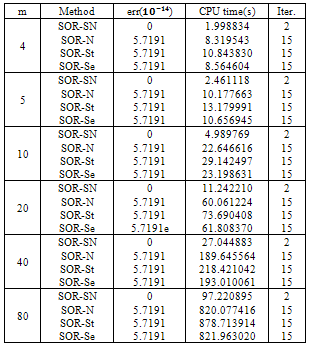
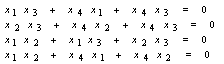 Its exact solution is
Its exact solution is 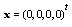 . For an initial guess we set
. For an initial guess we set 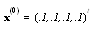 and
and 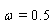 also for SOR-Secant method we set
also for SOR-Secant method we set 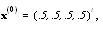
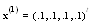 . The numerical results are given in Table 2.
. The numerical results are given in Table 2.
|
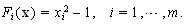 Its exact solutions are
Its exact solutions are 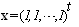 and
and 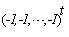 for different values of
for different values of 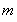 . For an initial guess we set
. For an initial guess we set 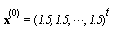 and
and 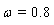 also for SOR-Secant method we set
also for SOR-Secant method we set 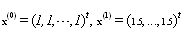 . The numerical results are given in Table 3.
. The numerical results are given in Table 3.
|
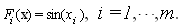 One of the exact solutions of the system is
One of the exact solutions of the system is 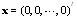 for different values of
for different values of 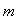 . For an initial guess we set
. For an initial guess we set 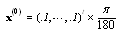 also
also 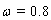 and for SOR-Secant method we set
and for SOR-Secant method we set 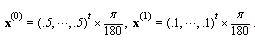 . The numerical results are given in Table 4.
. The numerical results are given in Table 4.
|
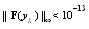 , where
, where 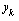 is the
is the 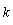 th approximation of the solution. Example 5 . We consider the following boundary value problem, which is given in[3]:
th approximation of the solution. Example 5 . We consider the following boundary value problem, which is given in[3]: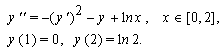 The exact solution of this problem is
The exact solution of this problem is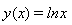 . To discretize the problem we use the second order finite difference method. The zeros of the following nonlinear functions will provide us an estimation of the solution of the problem:
. To discretize the problem we use the second order finite difference method. The zeros of the following nonlinear functions will provide us an estimation of the solution of the problem: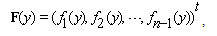 ,where
,where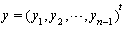 and for
and for 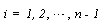 we have
we have 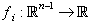 , such that
, such that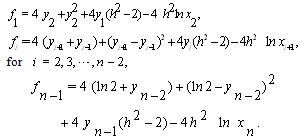 In the above system, the second order approximations are used for
In the above system, the second order approximations are used for 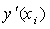 and
and 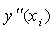 by step
by step 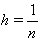 . By this step, we set the nodes
. By this step, we set the nodes 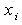 as:
as: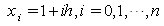 .Also,
.Also, 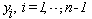 denotes the unknown
denotes the unknown 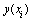 . In Table 5 some results can be observed. For any initial estimation, we analyze the number of iterations and CPU time needed to converge to the solution. The initial estimations used are:
. In Table 5 some results can be observed. For any initial estimation, we analyze the number of iterations and CPU time needed to converge to the solution. The initial estimations used are: 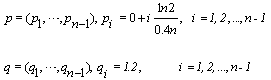 For SOR-secant in Table 5 we set
For SOR-secant in Table 5 we set 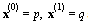 and in Table 6 we set
and in Table 6 we set 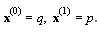 And
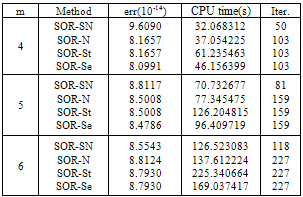
And 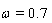 in both cases. As we can see from Tables 5 and 6 for all cases the number of iterations and CPU time for our new method are less than number of iterations and CPU time for the other methods.
in both cases. As we can see from Tables 5 and 6 for all cases the number of iterations and CPU time for our new method are less than number of iterations and CPU time for the other methods.
|
|
4. Conclusions
- In this paper, we have presented SOR-SN algorithm to solve systems of nonlinear equations. We have shown that our method is convergent. In comparison with another SOR type methods, such as, SOR-Newton, SOR-Steffensen and SOR-Secant methods, SOR-SN algorithm were better in CPU time and number of iterations.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML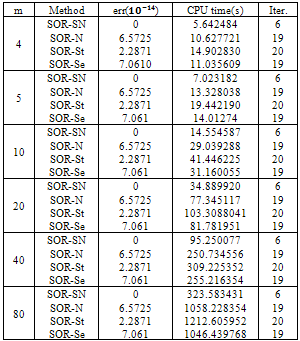
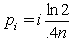 in Example 5
in Example 5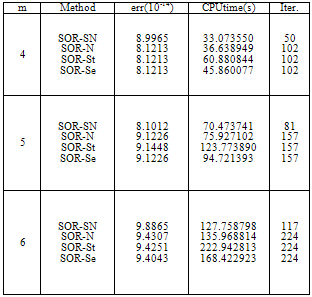
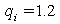 in Example 5.
in Example 5.