| [1] | Chawla, M. M., and Katti, C. P., 1982, Finite difference methods and their convergence for a class of singular two-point boundary value problems, Numer. Math, 39, 341-350 |
| [2] | Chawla, M. M., Mckee, S., and Shaw, G., 1986, Order h2 method for a singular two-point boundary value problem, BIT, 26, 326-381 |
| [3] | El-Gebeily, M. A., and Abu-Zaid, I. T., 1998, On a finite difference method for singular two-point boundary value problems, IMA J. Numer. Anal, 18, 179-190 |
| [4] | Pandey, R. K., and Singh, R. K., 2004, On the convergence of a finite difference method for a classof singular boundary value problems arising in physiology, Journal of Computational Applied Mathematics, 166, 553-564 |
| [5] | McElwain, D. L. S, 1978, A re-examination of oxygen diffusion in a spherical cell with Michaelis Menten oxygen uptake kinetics, J. Theor. Biol, 71, 255-263 |
| [6] | Duggan, R. C., and Goodman, A. M., 1986, Point wise bounds for a nonlinear heat conduction modelof the human head, Bull. Math. Biol, 48, 229-236 |
| [7] | Flesch, U., 1975, The distribution of heat sources in the human head: A theoretical considerationJ. Theor. Biol, 54, 285-287 |
| [8] | Garner, J. B., and Shivaji, R., 1990, Diffusion problems with mixed nonlinear boundary condition,J. Math. Anal.Appl, 148 422-430 |
| [9] | Ravi Kanth, A. S. V., and Bhattacharya, V., Cubic spline for a class of nonlinear singularboundary value problems arising in physiology, Journal of Computational Applied Mathematics, 2005 |
| [10] | Canuto, C., Hussaini, M. Y., Quarteroni, A., and Zang, T. A., Spectral Methods in Fluid Dynamics, Springer-Verlag, New York, 1987 |
| [11] | Shizgal, B., 1981, A Gaussian quadrature procedure for use in the solution of the Boltzmann equationand related problems, Journal of Computational Physic 41, 309-328 |
| [12] | Shizgal, B., and Chen, H., 1996, The quadrature discretization method (QDM) in the solution of the Shrödinger equation with non-classical basis functions, Journal of Chemical Physics 104(11), 4137-4150 |
| [13] | Gautschi, W., 1985, Orthogonal polynomials-constructive Theory and applications, Journal of Computational Applied Mathematics, 12/13, 61-75 |
| [14] | Golub, G. H., and Welsch, J. H., 1996, Calculation of Gauss quadrature rules, Mathematics of Computation, 23, 221-230 |
| [15] | Elnagar, G. N., and Kazemi, M. A., 2004, Numerical periodic optimal control: Apseudo-spectral Fourier approach, Numerical Functional Analysis and Optimization, 25, 707-724 |
| [16] | Elnagar, G. N., and Kazemi, M. A., and Razzaghi, M., 1995, Thepseudo-spectral Legendre method for discretizing optimal control problems, IEEE Tran. Automat. Cont, 40(10), 1793-1796 |
| [17] | Welfert, B. D., 1997, Generation of pseudo-spectral differentiation matrices, SIAM Journal of Numerical Analysis, 24, 1640-1657 |
| [18] | Hiltmann, P., Lory, P., 1983, On oxygen diffusion in a spherical cell with Michaelis-Menten oxygen uptake kinetics, Bull. Math. Biol, 45,661-664 |
| [19] | Asaithambi, N. S., and Goodman, J. B., 1989, Point wise bounds for a class of singular diffusion problems in physiology, App. Math. Comput, 30, 215-222 |
| [20] | A. Alipanah, M. Razzaghi and M. Dehghan, 2007, Nonclassical pseudospectral method for the solution of brachistochrone problem, Chaos, Solitons and Fractals, 34, 1622-1628 |
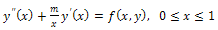
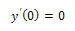
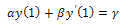
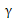 are real numbers and we assume that f(x, y) є{ L2[0,1]×R} is continuous,
are real numbers and we assume that f(x, y) є{ L2[0,1]×R} is continuous, 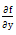 exists and continuous, and
exists and continuous, and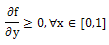 . For the case m = 2, α = γand β = 1 the existence and uniqueness of the solution (1)-(3) has been given in[18]. This work is based on the Michaelis-Menten kinetics[5] for the steady state oxygendiffusion in spherical cells, in which
. For the case m = 2, α = γand β = 1 the existence and uniqueness of the solution (1)-(3) has been given in[18]. This work is based on the Michaelis-Menten kinetics[5] for the steady state oxygendiffusion in spherical cells, in which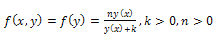
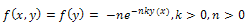
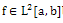 by using weighted interpolations of degree N of the form[11,12]
by using weighted interpolations of degree N of the form[11,12]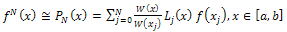
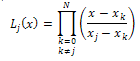
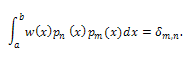 The polynomials satisfy a three-term recurrence relation[13]
The polynomials satisfy a three-term recurrence relation[13]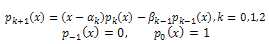
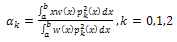
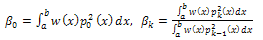
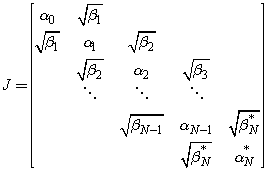
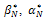 are obtained from the solution of the linear system of equations
are obtained from the solution of the linear system of equations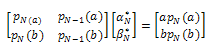
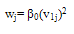
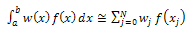
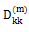 using the equation
using the equation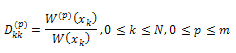 (b) Update
(b) Update 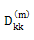 recursively using the equation
recursively using the equation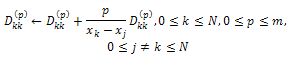 (2) Calculate the off-diagonal elements:(a) Initialize the off-diagonal elements using the equation
(2) Calculate the off-diagonal elements:(a) Initialize the off-diagonal elements using the equation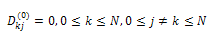 (b) Update
(b) Update 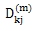 using the following equation
using the following equation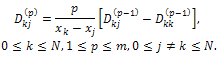 For practical numbers of collocation points, the above algorithm is generally sufficient.
For practical numbers of collocation points, the above algorithm is generally sufficient.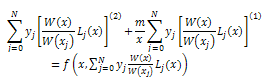
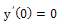
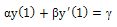
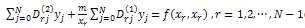
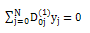
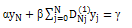
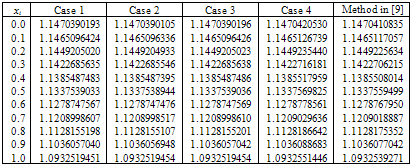
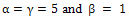 . Numerical results for cases given in Table 1, be given in Table 2, and numerical results with other methods be given in Table 3.
. Numerical results for cases given in Table 1, be given in Table 2, and numerical results with other methods be given in Table 3.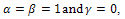 (ii)
(ii) 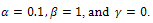 Table 4, shows numerical results for case (i) and all weighted functions given in Table 1. Also in Table 5, numerical results for case (ii)
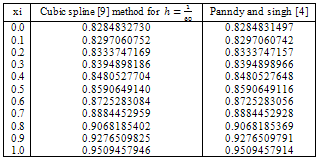
Table 4, shows numerical results for case (i) and all weighted functions given in Table 1. Also in Table 5, numerical results for case (ii) 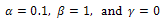 together with results of cubic spline[9] of Kanth and Bhattacharya are given.
together with results of cubic spline[9] of Kanth and Bhattacharya are given. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
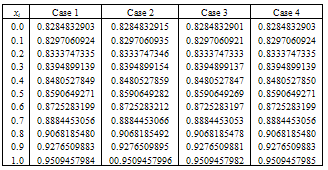
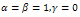 and for N = 10.
and for N = 10. 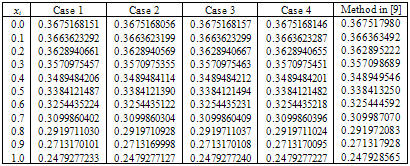
 and for N = 10
and for N = 10