1. Introduction

Block-Pulse functions (BPFs), a set of orthogonal functions with piecewise constant values, are studied and applied extensively as a useful tool in the analysis, synthesis, identification and other problems of control and systems science. In comparison with other basis functions or polynomials, BPFs can lead more easily to recursive computations to solve concrete problems[1] and among piecewise constant basis functions, the BPFs set has proved to be the most fundamental[2,3]. The complete details for BPFs are given in[1,4]. These functions have been directly used for solving different problems specially integral equations[5-10] as VIEs2[1] (and references therein).

There are some iterated methods for solving integral equations for example the iterated collocation and Galerkin methods. These methods are studied and applied by many researchers[11,12]. Sloan[13] showed that an iterated solution of a VIE2 is always a good idea if the initial guess is the solution obtained by the Galerkin method, regardless of the size of 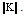With collocation, the iterated solution is not always an improvement on the original collocation solution, but it is for many cases of interest[11].

In the present work, an iterated method for solving VIEs2 is applied. Using Block-Pulse functions (BPFs) and operational matrix of integration, VIE2 can be transformed to a lower triangular system of algebraic equations (direct method). Then the solution of this system is used to determine a new numerical solution of VIE2 which we call iterated Block-Pulse method. The results of convergence show that the solution of this method can be at least as rapid as that of solution of direct method.

Section 2 of the paper introduces some preliminaries which are used through out this paper. The relations with small modifications of[1] are rewriten for the direct method in section 3. Then an approximation of a VIE solution is computed using iterated Block-Pulse method. The results of convergence and a error bound are given in section 4. Numerical examples in section 5 illustrate efficiency and accuracy of the proposed method at mid-point of every subinterval. These results are compared with the results of direct method, collocation method and iterated collocation method.

2. Preliminaries: Block-Pulse Functions

We start by repeating some definitions, notations and basic facts; For more details see[8,15].

2.1. Definition

Let 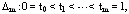denote an uniform mesh on [0,1] with

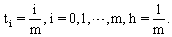(1)

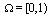An m-set of BPF's is defined on as

where 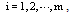with a positive integer value for m.

There are some properties for BPF's, the most important properties are disjointness, orthogonality and completeness.

2.2. Vector Form

The set of BPF's is written as

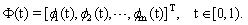(2)

So the disjointness property of BPF's follows

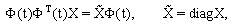(3)

where x is an m-vector. Also, for any m x m matrix B

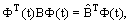(4)

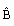where is a diagonal of matrix B.

2.3. BPF's Expansion

A function 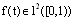, can be expanded by BPF's as

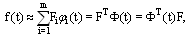(5)

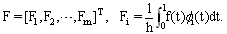(6)

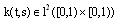Also kernel , can be expanded as

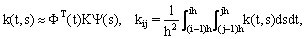(7)

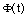where and 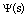are and dimensional BPF vectors respectively, and K is the 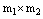Block-Pulse coefficients matrix with k_ij.

In this work, we set 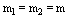and .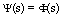

2.4. Operational matrix of integration

Integral of 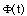is approximated by the following operational matrix of integration. This matrix is Teoplitze, so it can be used easily.

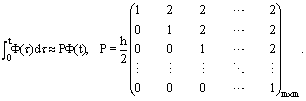(8)

Also, from[8], we have

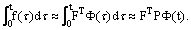(9)

3. Method: An Iterated Method for Solving a VIEs2

In this section, an iterated method for solving linear Volterra integral equations of the second kind (VIEs2) is introduced. Here the BPFs are used to solve a VIEs2 directly. Then by using the obtained solution of Direct method, this integral equation is solved for second time. This new approximation is often an improvement on solution of the Direct method.

We consider a Volterra integral equation of second kind as

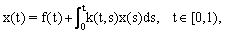(10)

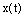where is unknown function, 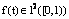and 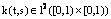are known.

3.1. Direct Method

The BPFs can be used to determine the numerical solution of Eq.(10) directly. The relations with small modification of [8] can be rewritten.

Setting approximation of functions f, x and k with respect to the BPFs by using (5) and (7) in Eq.(10), we have

Using (3) and (9) follows:

in which 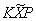is an 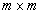matrix. By Eq.(4), we have

where 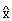is an 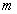-vector with components equal to the diagonal entries of matrix 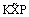as

So, Eq.(10) reduce to a linear lower triangular system as

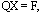(11)

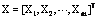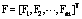with , and

where K is the m x m the Block-Pulse coefficients matrix with 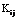that was defined in previous section. Unknown coefficients 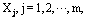are then calculated by solving this linear equations system. is the solution of Eq.(10) by using direct method.

3.2. Iterated Block-Pulse method

The BPFs can be used for solving Eq.(10) again. Now by using the solution of direct method, an approximation of solution x(t) of Eq.(10) is sought as

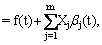(12)

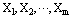where is the solution of the linear equations system (11) and

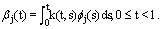(13)

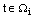Using the definition of the BPFs and the assumption that , (12) and (13) can be written as

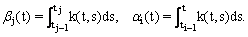(14)

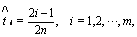Now an auxiliary mesh can be introduced as and 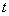can be replaced in (14) by 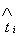. This method is called the iterated Block-Pulse method.

4. Error Bound and Convergence of Method

In this section, convergence of the iterated Block-Pulse method is considered. An error bound is given for obtained solution of this method. Eqs.(10) and (12) can be written in the operator form

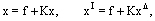(15)

respectively. Using (15), we have

and

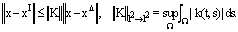(16)

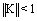If , then the convergence of 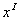to 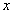is at least as rapid as that of 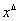to x.

5. Numerical Examples

In this section, the proposed method is used to determine the numerical solution of some examples. The numerical results are given in the tables for the error of approximation at the mid-point of every subinterval with 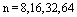. These results are compared with the results of direct, collocation and iterated collocation methods. The maximum norm of error for iterated Block-Pulse, direct, collocation and iterated collocation methods is denoted with 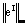, , 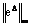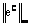and 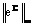, respectively. In the collocation method, BPFs are applied as a set of basis functions.

Example 1. Consider the Volterra integral equation of second kind [5]:

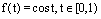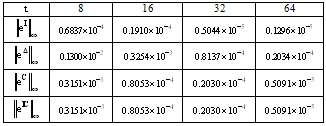
where . The exact solution of this equation is .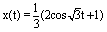

See Table 1 for numerical results of the maximum norm of error by using four methods at mid-point of every subinterval. The results show that the error of the iterated Block-Pulse method is smaller than the error of the direct method.The collocation method and the iterated collocation method have the same results. The error of the iterated Block-Pulse method is smaller than the error of the iterated collocation method.

Table 1. Errors of four methods for Example 1

Example 2. For the Volterra integral equation of second kind [5]:

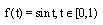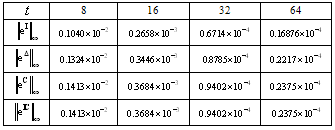
with , the exact solution is .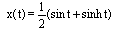

Table 2 shows numerical results for the maximum norm of error by using four methods at the mid-point of every subinterval. The maximum norm of error for the iterated Block-Pulse method is smaller than all the others. But, the numerical results for this example are very close to each other.

Table 2. Errors of four methods for Example 2

Example 3. The Volterra integral equation of second kind [9]:

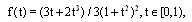where has the exact solution 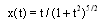. See Table 3 for numerical results of the maximum norm of error by using four methods at the mid-point of every subinterval. The maximum norm of error for the iterated Block-Pulse method is smaller than all the others. But, the numerical results for this example are very close to each other.

Table 3. Errors of four methods f or Example 3

6. Conclusions

In the present paper, a new iterated method for solving VIEs2 using BPFs was proposed. This method initially used the solution of the direct method to obtain the more accurate solution. The convergence and error analysis of this method were given. The results of convergence showed that the solution of this method can be at least as rapid as that of direct method. The numerical results of this method were compared with direct, collocation and iterated collocation methods. Similar to the iterated collocation method, the iterated solution is not always an improvement on the original direct solution, but it is for many cases of interest.