1. Introduction

This paper will discuss the Atom-bond connectivity index, its origins, its uses and its applications. The central topics of discussion for this paper will include: an investigation of the Furtula examples (provided through a personal communication), an exploration of the structure of the maximal and minimal chemical trees for the ABC index, and the contribution of certain types of vertices and edges to the ABC index of the graph as a whole. It will also consider graphs from a specific class Γ (to be defined later) and their ABC indices.

2. Formulation and History of the ABC Index

The atom-bond connectivity index, (ABC index), was first proposed by Ernesto Estrada in 1998. Estrada is a Cuban mathematician born in 1966. He is currently a professor and chair in Complexity Sciences at the University of Strathclyde in Glasgow, Scotland. The ABC index is a new topological index that has proven to be a valuable predictive index in the study of the heat of formation in alkanes[1]. For those who may not be familiar with alkanes, these are any of the series of saturated hydrocarbons having the general formula C_nH_2n+2, including methane, ethane and propane.

The ABC index comes from the connectivity index, χ, which was introduced in 1975 by Milan Randić[1]; however, the connectivity index deals with molecular branching. Estrada wanted to take into account the many physico- chemical properties that are not dependent on branching; thus, the ABC index was born.

2.1. Formulation

The ABC index is defined as follows:

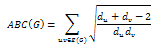where the summation goes over all the edges of G, d_u and d_v are the degrees of the terminal vertices u and v of edge uv and E(G) is the set of edges of G with cardinality m = |E(G)|.

2.2. Example

Let G be the following graph

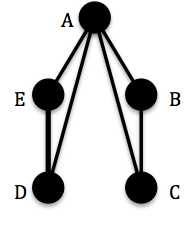
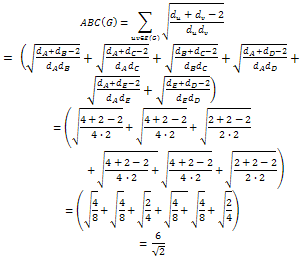
2.3. Chemical Trees and Some Examples

A tree in graph theory is any connected graph without a cycle or, in other words, an undirected graph in which any two vertices are only connected by exactly one simple path. Chemical trees are trees that have no vertex with degree greater than 4.

Examples of chemical trees:

Chains:

Trees:

The following are not chemical trees:

Graphs of vertex degree greater than 4 and graphs with cycles: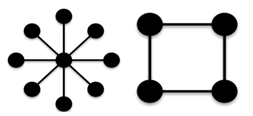

3. The ABC Index of Chemical Trees

This section of the paper will focus on the properties and applications of the ABC index on chemical trees. First, there will be an exploration of the contribution of specific types of edges to the ABC Index of a chemical tree and then a table will be developed to describe the contribution of specific edges more efficiently.

3.1. Contribution of Specific Edges

Contribution of a pendant edge (an edge of a graph is said to be a pendant edge if one of its vertices is of degree 1):

Let d equal the degree of the terminal vertex of a pendant edge uv that is not one.

Let e be the pendant vertex (e=1).

Then the contribution of the edge uv to the graph is given by:

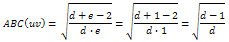Contribution of an edge uv whose terminal vertices are of degree d and 2:

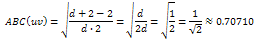Contribution of an edge uv whose terminal vertices are of degree 1 and 3:

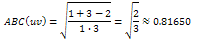Contribution of an edge uv whose terminal vertices are of degree 1 and 4:

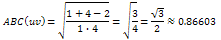Contribution of an edge uv whose terminal vertices are of degree d and 3:

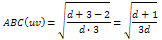Contribution of an edge uvwhose terminal vertices are of degree d and 4: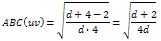

3.2. Table of Edge Contributions

Thus one can develop the following table in order to increase the ease with which one can calculate the ABC index of a graph G.

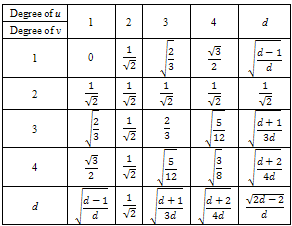
4. Chemical Trees of Minimal ABC Index

In this section, we will establish some notation to be used throughout the rest of the paper. There will also be an exploration of the notion of chemical trees of minimal ABC indices including a discussion and examination of the examples provided by Boris Furtula in a personal communication. (Furtula will be discussed in greater detail in the section 4.3).

4.1. Notation

In this section, it is necessary to establish notation for certain types of edges. Let an 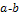edge be an edge with a terminal vertex of degree 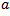and the other terminal vertex of degree 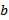. For example, a 3-4 edge is an edge between vertices of degree 3 and 4 respectively. Also let 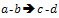denote a transformation of an 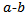edge to a 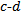edge. For example, 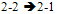means that a 2-2 edge was transformed into a 2-1 edge by adding or removing certain vertices and edges as specified in each unique case presented.

4.2. Finding Chemical Trees of Minimal ABC Index

First, let n be the number of vertices in the chemical tree G. At first glance, the obvious choice for the shape of a chemical tree of minimal ABC index would seem to be the chain. In fact, this is true for chemical trees with n≤6.

n=2

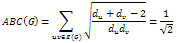This is the only possible arrangement for a chemical tree with 2 vertices.

n=3

The chain is once again the only option.

n=4

n=5

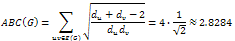
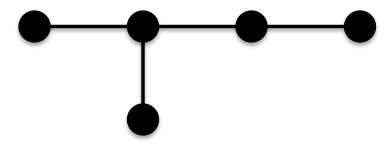
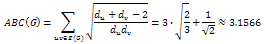
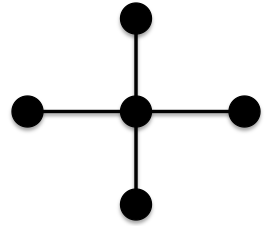
n=6

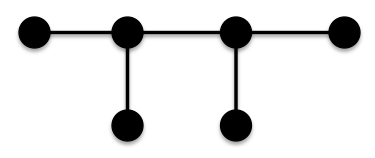
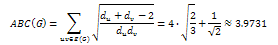
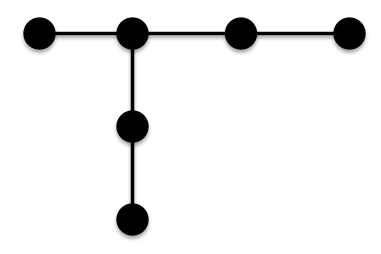
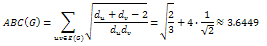Thus for n≤6, the chain has the minimal ABC index.

4.3. Boris Furtula and Chemical Tress with More than 6 Vertices

Boris Furtula was born in 1978 in Kragujevac, Serbia. He is a professor in the Faculty of Science at Kragujevac University where he studied for all of his post-secondary education. Furtula is a leader in the study of chemical graph theory, known for his extensive research on the ABC Index.

According to a personal communication with Furtula[3], there are two possible chemical trees with 7 vertices and minimal ABC indices.

The first is the chain:

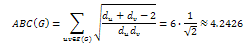And the second is the following tree:

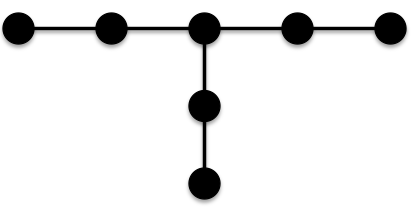Note that all edges in this tree have at least one terminal vertex of order 2; this means that all the edges contribute the same amount to the ABC index 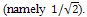Thus, the ABC index of this formation is equal to the ABC index of the chain with 7 vertices.

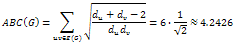Therefore, there are two different chemical trees with 7 vertices of minimal ABC index.

Similarly for chemical trees with n=8, there are two different trees with 8 vertices of minimal ABC index.

The chain:

And another tree:

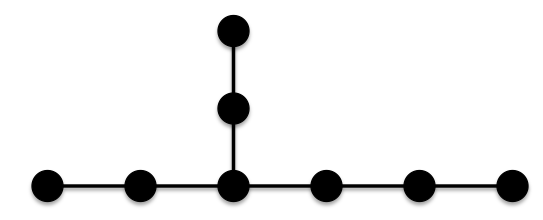Note that similar to the tree of minimal ABC index for 7 vertices, all of this tree’s edges have at least one vertex of degree 2.

For 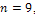, there are 4 trees of minimal ABC index including the chain.

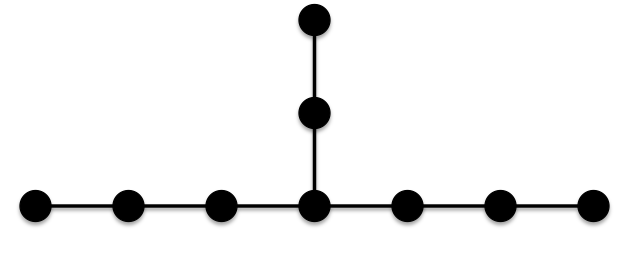
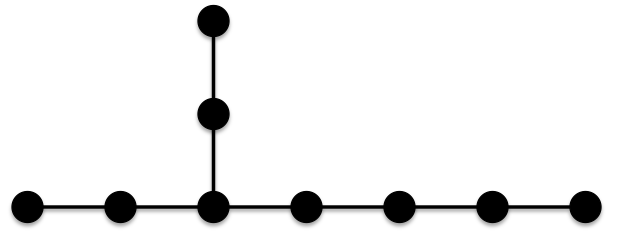
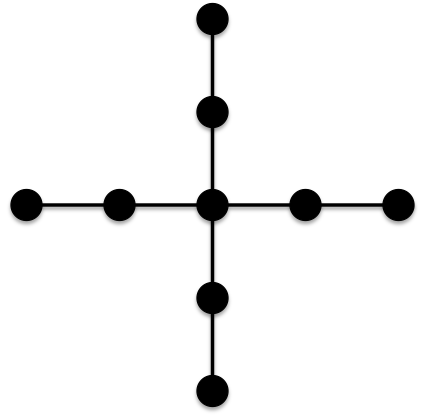All four of these trees have edges which each have at least one terminal vertex of degree 2. Thus, all the edges in these trees contribute the same amount to the ABC index and since each of these graphs has 8 edges, all four of these trees have the same minimal ABC index as the chain of 9 vertices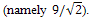

4.4. Chemical Trees whose Chain is not among the Trees of Minimal ABC Index

Thus far, the chain has been among the trees of minimal ABC index for 2≤n≤9; however, this is not the case for n≥10.

Consider the chemical trees with n=10.

It seems that from the previous examples that the minimal ABC index of trees with n=10 would be 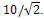. This would be the case if all the edges of the tree had at least one terminal vertex of degree 2. But what if the tree could have an edge that would contribute less than one which has a vertex of degree 2 (namely less than ).

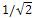Consider the following tree with n=10:

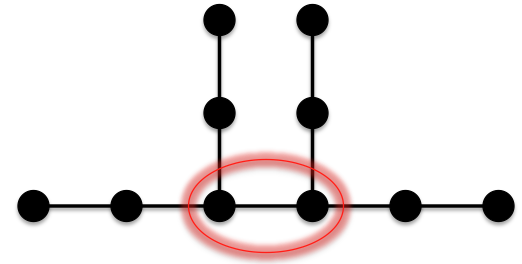All of this tree’s edges have at least one vertex of degree 2 except for the one that is circled. This edge is between two vertices of degree 3.

The contribution of the circled edge is as follows:

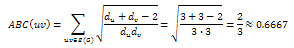Compare the contribution of this edge to an edge that has at least one of its terminal vertices of degree 2.

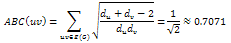Thus, the indicated edge with vertices of degree 3 contributes less than one of the edges of a chain would and so the ABC index of this tree is less than the ABC index of a chain of 10 vertices. In fact, it is the only tree with 10 vertices of minimal ABC index according to Furtula.

5. Developing a Method for Determining the Chemical Tree of Minimal ABC Index

Clearly then, a method for determining the chemical trees of minimal ABC index is to try to establish a combination of edges which contribute less than

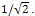From the table above, these edges that contribute less than 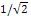are the following: a 3-3 edge, 3-4 edge and a 4-4 edge. (Note that here we do not consider edges of degree greater than 4 because we are currently focusing on chemical trees).

5.1. Examining the Tree of Minimal ABC Index with 11 Vertices

According to Furtula, the following tree is of minimal ABC index for 11 vertices:

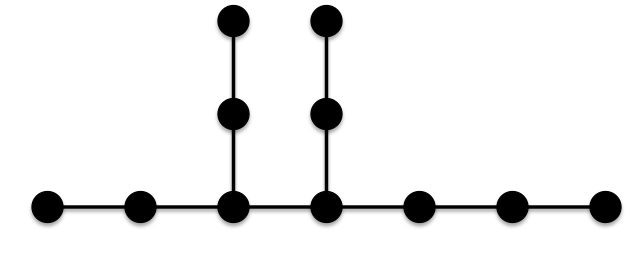
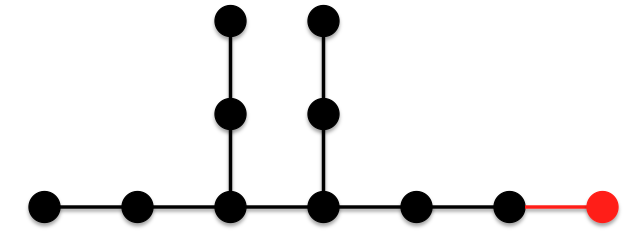Note that this tree is very similar to the tree of minimal ABC index for 10 vertices; it simply has one more vertex and edge added to the horizontal chain.

Let us explore the different ways one could form a tree with 11 vertices to try to determine why the new edge and vertex were placed where they were.

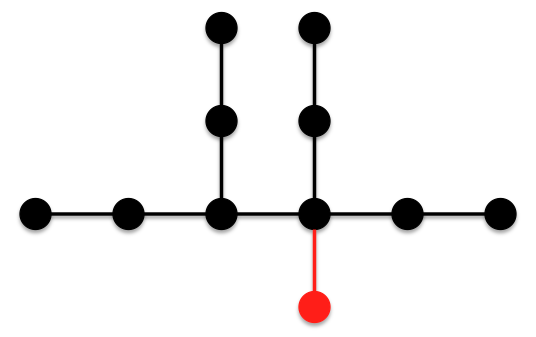The original given by Furtula:

Number of 2-1 edges:4

Number of 2-2edges:1

Number of 3-2edges:4

Number of 3-3 edges:1

The example above (Example A):

Number of 2-1 edges:4

Number of 2-2 edges:0

Number of 3-2 edges:2

Number of 3-3 edges:0

Number of 3-4 edges:1

Number of 4-1edges:1

Number of 4-2 edges:2

It seems that to go from the original given by Furtula to Example A the following transformations take place:

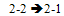so in terms of contributions there in no change to the ABC Index

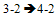no change

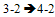no change

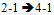CHANGE: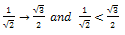

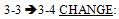
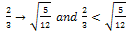Since any edge with at least one terminal vertex of degree 2 will contribute 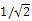to the ABC index regardless of the degree of the other terminal vertex, no change occurs to the ABC index from the first three transformations. However, the last two transformations result in a greater contribution to the ABC index and thus Furtula’s tree with 11 vertices is still the minimal tree.

Let us try another transformation (Example B):

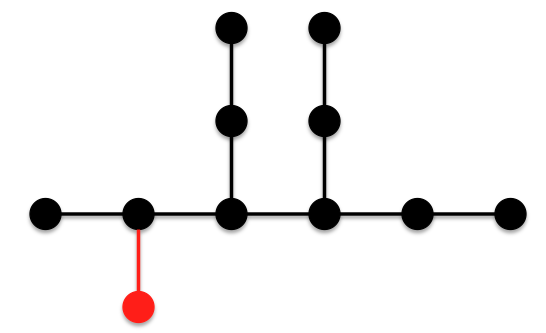We have now lost two 2-1 edges and gained two 3-1 edges

We have also lost a 3-2 edge for a 3-3 edge.

Since the contribution of a 2-1 edge is less than the contribution of a 3-1 edge, this transformation increases the ABC index.

However, as mentioned above, the 3-3 edge contributes less than the 3-2 edge so we must calculate the decrease in the ABC index and ensure that it is less than the increase caused by the first transformation.

Contribution of a 2-1 edge:

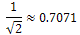Contribution of a 3-1 edge:

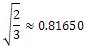Thus the total increase to the ABC index is:

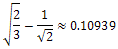Contribution of a 3-2 edge:

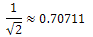Contribution of a 3-3 edge:

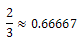Thus the total decrease to the ABC index is:

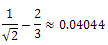Therefore, this transformation ultimately results in an increase in the ABC index and Furtula’s tree is still the minimal example.

What about the following tree, call it example C?

Here we see that there is no change to the ABC index from the transformation; however, this is not a new formation. In fact, this tree has the same ABC index as Furtula’s for the simple reason that it is isomorphic to Furtula’s tree.

5.2. Determining the Tree of Minimal ABC Index with 12 Vertices

Let us try to construct a tree of minimal ABC index for 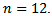Given what we now know about the contribution of certain edges, we would like to have as many 3-3, 3-4 and/or 4-4 edges as possible

Try starting with a vertex of degree 4

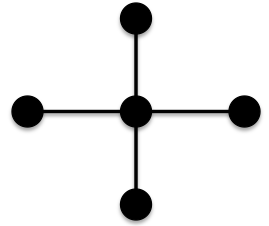Now let us connect this tree with another tree to form a 4-4 edge.

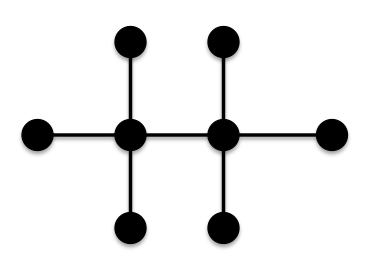Here we have used 7 of the 12 vertices.

We know that 4-1 edges contribute more than 4-2 edges so let us add a pendant edge to each of the pendant vertices to develop the following tree:

This tree has 12 vertices but is this tree of minimal ABC index?

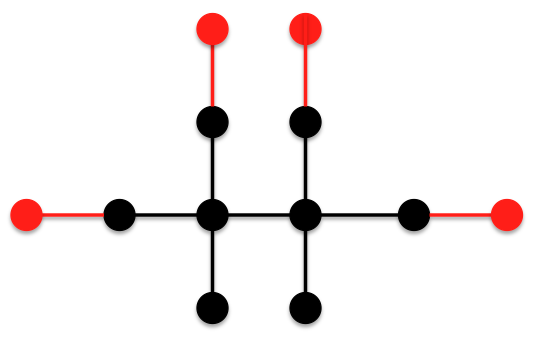Note that this tree still has two 4-1 edges. The question is: does it make sense to take one of these 4-1 edges and add it to one of the pendant edges?

This would change one of the vertices of degree 4 to degree 3 so instead of having a 4-4 edge and two 4-2 edges we would now have a 3-4 edge and two 3-2 edges. The 3-2 edges will contribute the same as the 4-2 edges so they are not interesting. The question becomes: does a 3-4 edge contribute less than a 4-4 edge?

The answer is no. A 3-4 edge contributes slightly more than a 4-4 edge. So the following tree is not the minimal tree:

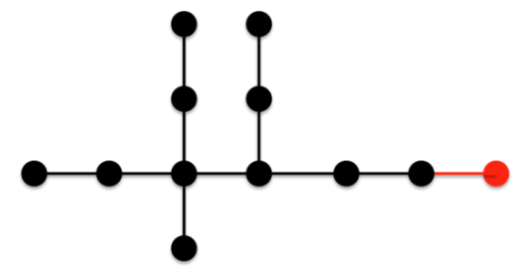What if we take this edge and move it as follows so that we form another 4-2 edge instead of a 4-1 edge?:

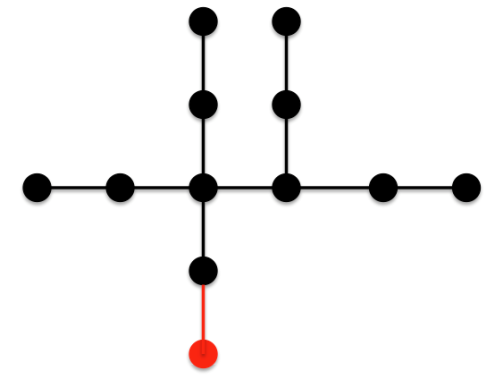Now we have a slight increase in the ABC index because a 4-4 edge becomes a 3-4 edge but we also change a 4-1 edge to a 4-2 edge, which decreases the ABC index.

Comparing the increase and decrease we see that the decrease is larger than the increase and thus this tree has a smaller ABC index than the previous trees.

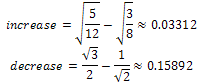Thus, we establish the tree of minimal ABC index with n=12 (Confirmed by Furtula)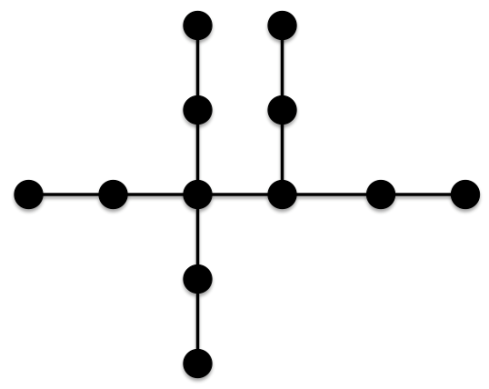

6. Class Γ and Graphs of Maximal ABC Index

Another leader in chemical graph theory is Indian mathematician Kinkar Das who is currently employed in the Department of Mathematics in Sungkyunkwan University, Korea. His research interests include Spectral Graph Theory, Molecular Graph Theory, Algorithm and Complexity, General Graph Theory, Discrete Mathematics, Combinatorics, and Graph Labeling. He has also worked with Furtula to publish findings on the ABC Index. The following section is a brief description of the findings outlined by Das in his article: Atom-bond connectivity index of graphs published in 2010. Here, the discussion will center on a specific class of graphs described by Das and some results regarding graphs that are not chemical trees (such as those in class 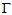) will be introduced.

6.1. The Class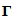

Let us explore another class of graphs, 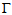postulated by Kinkar Das. Let H be a graph in 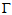and let 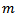be the number of edges in H. Then:

1. H is a connected graph

2. H has minimum vertex degree.

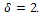3. H has q edges between vertices of maximum degre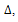e where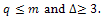

4. H has 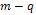edges for which at least one of the terminal vertices has degree .

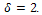And q is given by:

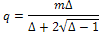Thus, an edge, say 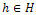, is of one of two possible types: either 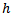has at least one terminal vertex of degree 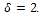or both the terminal vertices of h are of maximum degree [1].

6.2. ABC Index of Graphs from Class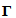

The characteristics of a graph H in Class 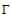imply that the contribution of an edge h to the ABC(H) is either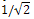

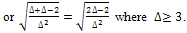Therefore, we deduce the following equation for the ABC(H):

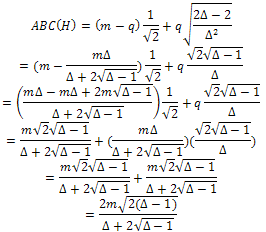Therefore,

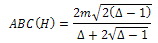Note that any graph T which is tree cannot be in 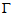for the simple reason that a tree has pendant vertices of degree 1 and thus the minimum vertex degree for any tree is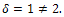

6.3. Examples

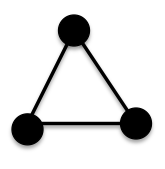
Now let us examine some examples of graphs from class 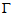. As mentioned above, these graphs will not have any pendant edges. Let us start with the most basic cycle, K₃.

This graph, K₃ is connected and it has minimum vertex degree 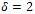but 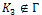since it has maximum vertex degree

Is ?

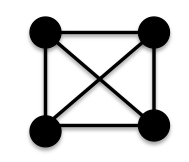K₄ is connected, has maximum vertex degree 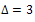but now K₄ has minimum vertex degree

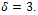What happens if we remove one of the diagonal edges?

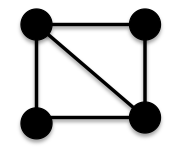Call this graph A. A 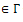since A is connected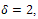, has , has 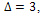and all of its edges are either between vertices of maximum degree or between vertices with at least on vertex of degree 2.

Let us try adding triangular shaped graphs onto some of the vertices to see if we can generate another example of a graph from the class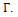

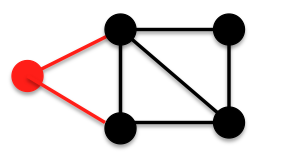This graph, call it B, is not in 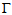. It has 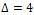and it has a 4-3 edge. This edge is not between two vertices of maximum vertex degree, nor does it have at least one vertex of degree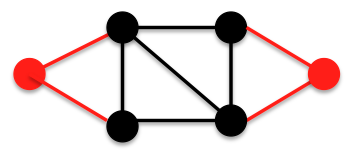

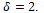Let us try to remedy this by adding a second triangular graph to the right side of the graph B as follows:

We still have 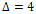and 4-3 edges.

Let us try making the core a complete graph K₄ by adding an edge as follows:

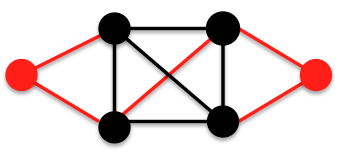Now check that this graph, call it C, meets all the criteria in order for it to belong to

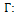1. It is connected.

2. It has minimum vertex degree

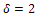3. It has 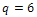edge between vertices of maximum degree

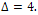4. It has 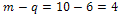edges for which at least one of the terminal vertices is of degree

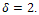Thus, 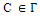and we can now easily calculate its ABC index because we know that for all graphs ,

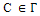Consider the following graph D: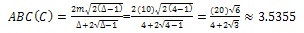

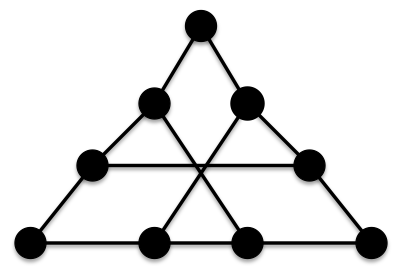
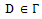since D is connected, D 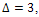has D has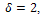 and all of the edges of D are either between two vertices of degree 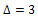or have at least one vertex of degree

.

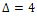In fact, we can add 3 more edges to form a graph E with maximum degree where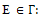

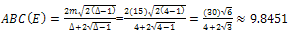And, we can add 6 edges to turn the core of the graph E into K₆ and generate a new graph F as follows: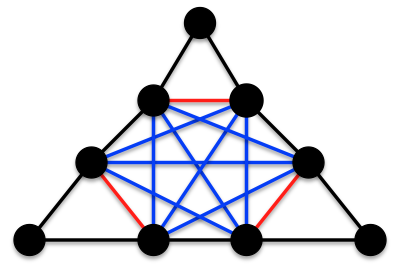

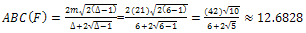Now we can add 3 triangles to graph F to form the following graph G that is also in

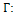In G,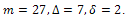

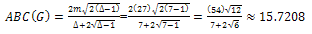
6.4. Alternative Formulation of the ABC Index

Das states the ABC index equivalently as follows:

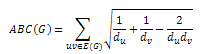This formulation allows for the taking into account of the modified second Zagreb index which is equal to the sum of the products of the reciprocal of the degrees of pairs of adjacent vertices, that is,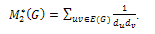

.

This modified second Zagreb index is used by Das is the formulation of many theorems and their subsequent corollaries establishing upper and lower bounds on the ABC index of specific simple connected graphs with particular characteristics[1].

6.5. Graphs of Maximal ABC Index

It is generally accepted that the graph of maximal ABC Index with n vertices is, K_1,n-1 commonly known as the star graph[5].

Brief reasoning behind this notion:

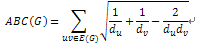For a pendant edge uv, with d_u=1 and d_v=v,

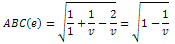And obviously, to maximize this you would take the highest value for v possible, thus you need all the edges to be of the from 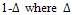is the maximum vertex degree in the graph G.

But why choose to have all pendant edges?

Well, if we look at the original formulation of the ABC Index:

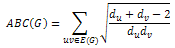Note that in order to maximize this equation we need to make d_u+d_v-2 as large as possible while keeping d_ud_v as small as possible. And, as it turns out, this is achieved by making one of the degrees 1 and the other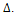

7. Conclusions

The problem of determining the tree(s) that minimize(s) the ABC index for fixed number of vertices n is still open. It is difficult even when the maximum vertex degree is limited to 4, i.e. on chemical trees. Here we suggested an approach based on the contribution of certain edges. Conceivably, one can devise a procedure that identifies an edge to be replaced and place in the tree where it has to be reinserted in order to minimize the ABC index. Our work serves as a good source of heuristics on which edges should be considered candidates for replacement, as well as what structural components should be sought.

ACKNOWLEDGEMENTS

Dr. Vassilev’s work is supported by NSERC Discovery Grant. Laura Huntington wants to acknowledge the help of Dr. Vassilev during the work on this paper. Both authors would like to acknowledge the friendly and collegial atmosphere at the 2^nd Annual Workshop on Algorithmic Graph Theory held at Nipissing University on May 16-20, 2011. It is there where the idea for this research was conceived and informally discussed. We also acknowledge the correspondence of Dr. Darko Dimitorv, Freie Universität, Berlin, who helped us identify relevant literature on the problem.