-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(2): 122-129
doi: 10.5923/j.am.20110102.20
Mathematical Modeling of Filtration from Canals and Sprinklers of Irrigation Systems
E. N. Bereslavskii , N. V. Likhacheva
GOUVPO , Saint-Petersburg State University of Civil Aviation
Correspondence to: E. N. Bereslavskii , GOUVPO , Saint-Petersburg State University of Civil Aviation.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We consider several schemes of seepage flows from canals and sprinklers of irrigation systems through the soil layer, underlain good underlying permeable confined aquifer or water-resistant base. For their study and formulated using the method of P.Y. Polubarinova-Kochina solved multivariable mixed boundary value problems of the theory of analytic functions. On the basis of these models are developed algorithms for calculating the size of the saturated zone in situations when the filter has to evaluate the combined effect of the painting movement of such important factors as seepage back pressure from the underlying confined aquifer or an impermeable base, cross-sectional shape and channel the power supply level of water in it , capillarity of the soil and evaporation from the free surface of groundwater. The results of calculations for all the schemes are compared with the same filtration filter parameters depending on the shape of the channel as a power source (canal or irrigation), and the type of foundation soil layer (silnopronitsaemy confined aquifer or aquitard).
Keywords: Filtering, Channel, Irrigation, Soil Capillarity, Pressure, Evaporation, Infiltration, Free Surface, The Complex Flow Velocity Method Polubarinova-Cochina, Conformal Mapping
Cite this paper: E. N. Bereslavskii , N. V. Likhacheva , "Mathematical Modeling of Filtration from Canals and Sprinklers of Irrigation Systems", Applied Mathematics, Vol. 1 No. 2, 2011, pp. 122-129. doi: 10.5923/j.am.20110102.20.
Article Outline
1. Introduction
- It is known (see, eg, reviews[1-4]) that the mathematical modeling of filtration flows from canals and sprinklers of irrigation systems used a variety of research methods applied analytic functions introduced in[5-9], the method of conformal mappings of the rectilinear polygons based on the application of the Schwarz- Christoffel formula[10-13] and functions Riesenkampf and Verigin[14], the method of P.Y. Polubarinova-Cochina, based on the application of the analytic theory of linear differential equations of Fuchs class[15-18], the theory of inverse boundary value problems[19,20], etc. Despite the importance of these research studies in this direction so far alienated and not fully reflect the specific movements of the canals and sprinklers, which is characterized by the presence of such important factors as seepage back pressure from the underlying permeable aquifer well containing a pressurized underground (or artesian) water or water-resistant base, soil capillarity and evaporation (or infiltration) at the free surface of groundwater. All marked work associated with the presence of one or two of the three factors that significantly affect the simulated processes. Accounting for the simultaneous influence of these three characteristics of the filter has not become abroad domain of exact analytical solutions.In contrast to these studies in this paper, which is a continuation and development[21-25], both case of motion of the water of the canals and sprinklers are considered together, which apparently has not yet appeared in the literature. In this case it is shown that the solution for sprinklers obtained by solving the filtration problem for channels with a limit associated with the conformal mapping parameters contained in the required dependencies. Provides a uniform method of solving problems, which allows to consider four different schemes of the flow and take into account in the study at once all three filtration characteristics - capillarity, evaporation, and props - that is of considerable practical interest because it allows us to estimate the combined influence of these factors on the phenomenon. For this purpose, the method of P.Y. Polubarinova-Kochina[1-4], based on the use of conformal mapping of circular polygons. With the help of developed[26-29] methods of solving the corresponding linear differential equations of the Fuchs class, which are very common problems of underground hydromechanics solve mixed boundary value problem of multi-parameter theory of analytic functions. On the basis of the obtained exact analytical relationships and numerical calculations are carried out by hydrodynamic analysis of the influence of physical parameters of the schemes of flow on filtration characteristics. We give a comparison of the results of calculations for these schemes under the same filter characteristics depending on the shape of a channel-power sources of water (or irrigation canal) and the type of underlying soil base (well permeable confined aquifer or aquitard).
2. Filtration of the Channels in the Presence of the Basis of Well-Permeable Horizon Containing Pressurized Groundwater (Scheme 1)
- In fig. 1 shows a right-symmetric picture steady plane flow of an incompressible fluid by Darcy's law with known filtration coefficient к=const of channel width l with a shallow depth of water at uniform evaporation from the free surface of CE intensity ε (0 <ε <1), divided by the coefficient of filtration. At some depth from the bottom of the channel T is silnopronitsaemy pressure horizon FE, piezometric water level in which the
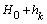 (
(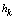
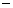 static height of capillary rise of groundwater[1,2]) above the horizontal interface between it and a layer of soil, which studies the movement. The channel width l, thickness of the soil layer T, the pressure (above the roof) in the underlying permeable horizon is well along
static height of capillary rise of groundwater[1,2]) above the horizontal interface between it and a layer of soil, which studies the movement. The channel width l, thickness of the soil layer T, the pressure (above the roof) in the underlying permeable horizon is well along 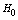 with the intensity of evaporation
with the intensity of evaporation 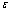 and high vacuum hk, due to capillary forces in the soil are given.
and high vacuum hk, due to capillary forces in the soil are given.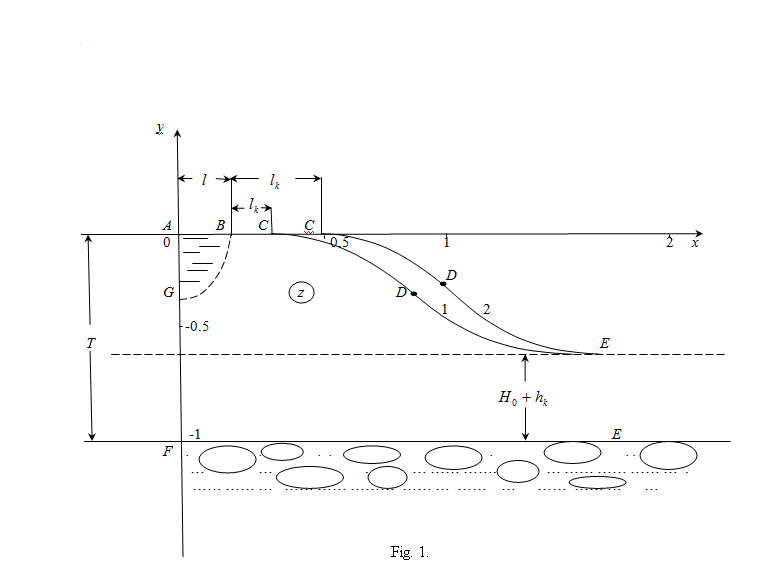 | Figure 1. The flow pattern with curved depression in filtering out of the canal (Figure 1, curve 1) and sprinkler (Fig. 2, curve 2) calculated at 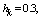 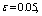 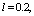 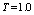 and and 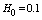 |
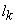 of the capillary spreading of water filtration and BC flow Q with the following boundary conditions:
of the capillary spreading of water filtration and BC flow Q with the following boundary conditions: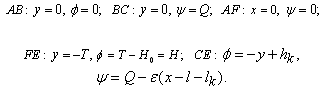 | (1) |
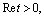
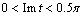 in the t plane, the flow region in accordance points
in the t plane, the flow region in accordance points 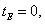
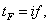

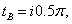
 and derivatives
and derivatives 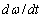 и
и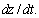 In fig. 2, a shows a complex velocity field
In fig. 2, a shows a complex velocity field 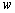 , corresponding to the boundary conditions (1), which is a circular quadrangle with a cut to the top of D, and the angle
, corresponding to the boundary conditions (1), which is a circular quadrangle with a cut to the top of D, and the angle 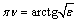 at the vertex C. Function effecting the conformal mapping of t on the field
at the vertex C. Function effecting the conformal mapping of t on the field 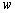 has the form
has the form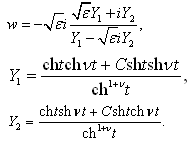 | (2) |
 | Figure 2. On integrated circuits 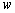 for speeds 1 and 2 (a) and figure 3, 4 (b) for speeds 1 and 2 (a) and figure 3, 4 (b) |
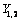 – are linearly independent integrals of the corresponding linear differential equation of Fuchs class[26-28], C - a suitable real constant conformal mapping.Applying the method of P.Y. Polubarinova-Cochina and taking into account the relation (2), as well as the fact that
– are linearly independent integrals of the corresponding linear differential equation of Fuchs class[26-28], C - a suitable real constant conformal mapping.Applying the method of P.Y. Polubarinova-Cochina and taking into account the relation (2), as well as the fact that 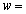
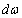 /
/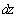 , we find a parametric solution of (1) as
, we find a parametric solution of (1) as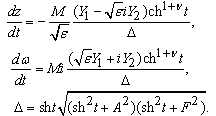 | (3) |
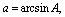
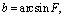 a and f (
a and f (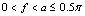 )– unknown ordinates of the points A and F in the plane t[21-23]. Integrating the representation (3) along the contour of the auxiliary field t, we can obtain expressions for the physical characteristics of the model
)– unknown ordinates of the points A and F in the plane t[21-23]. Integrating the representation (3) along the contour of the auxiliary field t, we can obtain expressions for the physical characteristics of the model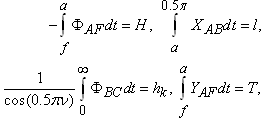 | (4) |
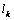 and
and 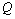 coordinates of points of depression
coordinates of points of depression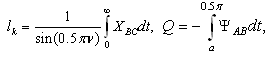 | (5) |
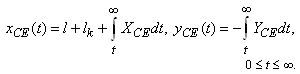 | (6) |
3. Filtration of the Irrigators in the Presence of the Basis of Well-Permeable Horizon Containing Pressurized Groundwater (Scheme 2)
- In fig. 1 shows the pattern of motion of the sprinkler borozdovogo type with a radius
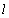 which is filled with water up to ground level, taken as a horizontal plane. During the initial review sprinkler replace a point source located at a point
which is filled with water up to ground level, taken as a horizontal plane. During the initial review sprinkler replace a point source located at a point 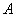 . Then the solution for the source is obtained by solving the problem of filtration for the channel (3) with the values of conformal mapping
. Then the solution for the source is obtained by solving the problem of filtration for the channel (3) with the values of conformal mapping 
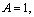 is at the confluence of the points A and B in the plane of flow.Further, according to[1,2,6,7], we take one of the lines of equal pressures, for example
is at the confluence of the points A and B in the plane of flow.Further, according to[1,2,6,7], we take one of the lines of equal pressures, for example  (shown in fig. 1 smooth curve) for the cross-section of the sprinklers with radius l, and let her
(shown in fig. 1 smooth curve) for the cross-section of the sprinklers with radius l, and let her  Under these conditions along portions of the border region z will continue to run the boundary conditions (1), and the complex velocity field
Under these conditions along portions of the border region z will continue to run the boundary conditions (1), and the complex velocity field  (fig. 2, a) and the unknown function (3) (6) retain their form. The formulas (4), (5) for the quantities
(fig. 2, a) and the unknown function (3) (6) retain their form. The formulas (4), (5) for the quantities 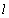 and
and 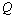 replaced by the following:
replaced by the following: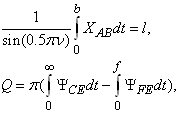 | (7) |
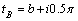 . Private and limiting cases of the model 2 in detail in[25].
. Private and limiting cases of the model 2 in detail in[25].4. Comparison of Numerical Results for the Channels (Scheme 1) and Sprinklers (Scheme 2)
- In fig. 1 shows the curves of depression during the filtration of the channels (left curve CE) and sprinklers (right curve CE), calculated with
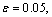
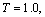
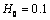 ,
, 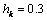 and
and 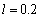 (baseline). The results of calculations of the influence of physical parameters
(baseline). The results of calculations of the influence of physical parameters 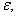
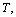
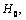
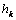 and
and 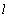 the width of the capillary spreading of the liquid flow rate
the width of the capillary spreading of the liquid flow rate 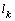 and filtration
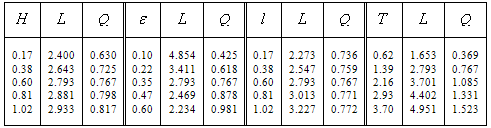
and filtration 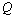 are shown in table. 1 and 2 (upper line corresponds to the sprinklers, the lower
are shown in table. 1 and 2 (upper line corresponds to the sprinklers, the lower 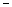 channel). In each of the blocks of the tables, which are separated by double vertical lines, varies in the allowable range is one of the above parameters, and values of other fixed base values. In fig. 3 shows a plot of the size
channel). In each of the blocks of the tables, which are separated by double vertical lines, varies in the allowable range is one of the above parameters, and values of other fixed base values. In fig. 3 shows a plot of the size 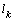 and flow
and flow 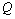 channels (curves 1) and sprinklers (curves 2) on the parameters
channels (curves 1) and sprinklers (curves 2) on the parameters 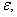
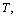
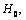
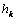 и
и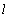 .Analysis of the data tables and graphs to the following conclusions.The increase in channel width and radius of the sprinkler, the pressure in the underlying aquifer and the height of the vacuum caused by capillary forces in the soil and reduce evaporation and capacity of the soil layer lead to increase the width of the capillary spreading of the water. Reduce evaporation and increase the backwater from the waters of the underlying horizon is accompanied by increase in the magnitude
.Analysis of the data tables and graphs to the following conclusions.The increase in channel width and radius of the sprinkler, the pressure in the underlying aquifer and the height of the vacuum caused by capillary forces in the soil and reduce evaporation and capacity of the soil layer lead to increase the width of the capillary spreading of the water. Reduce evaporation and increase the backwater from the waters of the underlying horizon is accompanied by increase in the magnitude 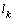 and, conversely, decrease the filtration rate
and, conversely, decrease the filtration rate 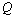 . A similar behavior is observed
. A similar behavior is observed 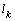 and
and 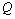 the values and decreasing capacity of the soil layer T. Thus, with respect to the filtration of the canals and sprinklers and evaporation capacity of the soil layer plays the same role as props, as the quantity
the values and decreasing capacity of the soil layer T. Thus, with respect to the filtration of the canals and sprinklers and evaporation capacity of the soil layer plays the same role as props, as the quantity 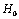 .
.
|
|
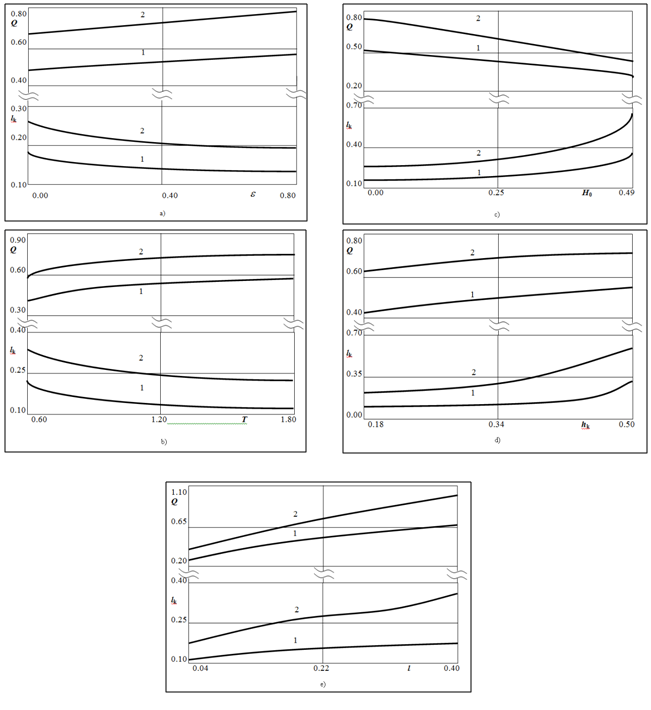 | Figure 3. Depending on the value 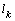 and and 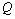 for all channels (1) and sprinklers (2) from for all channels (1) and sprinklers (2) from 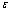 (a) at constant (a) at constant 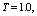 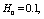 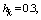 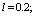 of (b) with constant of (b) with constant 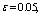 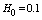 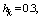 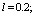 of of 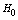 (c) with constant (c) with constant 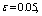 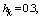 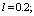 of of 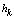 (d) with constant (d) with constant 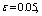 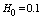 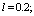 of of 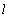 (e) at constant (e) at constant 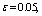 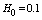 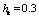 |
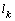 and the seepage flow
and the seepage flow 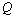 on the parameters
on the parameters 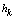 and
and 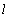 : with increasing height of capillary rise of water and the channel width or radius of irrigators
: with increasing height of capillary rise of water and the channel width or radius of irrigators 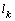 and
and 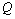 the value increases. The effect of evaporation on the filtration characteristics can be traced back to the left block of table. 1: The variation of the parameter
the value increases. The effect of evaporation on the filtration characteristics can be traced back to the left block of table. 1: The variation of the parameter 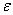 corresponds to the decrease
corresponds to the decrease 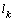 of 1.4 times, while
of 1.4 times, while 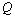 consumption changes by only 12-16%.The average block table. 1 allows us to determine the nature of the influence of layer thickness
consumption changes by only 12-16%.The average block table. 1 allows us to determine the nature of the influence of layer thickness 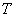 : the shallow horizon silnopronitsaemogo spreading width of the capillary water may exceed the height of the capillary vacuum. Thus, when
: the shallow horizon silnopronitsaemogo spreading width of the capillary water may exceed the height of the capillary vacuum. Thus, when 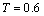 we have
we have 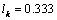 and therefore
and therefore 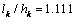 . With the increase in this ratio becomes even greater. The presence of the underlying horizon practically affect the values of
. With the increase in this ratio becomes even greater. The presence of the underlying horizon practically affect the values of 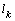 and
and 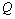 at
at 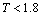 . At higher values
. At higher values 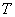 of the deviation of the values
of the deviation of the values 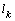 and
and 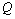 does not exceed 1%.We have said above is qualitatively the opposite nature of variation of the unknown quantities,
does not exceed 1%.We have said above is qualitatively the opposite nature of variation of the unknown quantities, 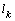 and
and 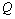 by varying the values of
by varying the values of 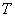 and
and 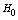 . Sections of the table 1 relating to the parameter
. Sections of the table 1 relating to the parameter 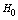 indicates that, on the contrary, at relatively large values of the overpressure ratio
indicates that, on the contrary, at relatively large values of the overpressure ratio 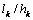 can also be very significant. For example, when
can also be very significant. For example, when 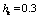 for
for 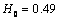 we get
we get 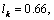 to so that the width of the capillary spreading of the water
to so that the width of the capillary spreading of the water 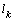 exceeds the height of capillary rise of liquids up to 120%.However, the greatest influence on
exceeds the height of capillary rise of liquids up to 120%.However, the greatest influence on 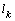 the capillarity of the soil has. From table 2 shows that the parameter
the capillarity of the soil has. From table 2 shows that the parameter 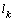 changes the width of the capillary spreading of the water
changes the width of the capillary spreading of the water 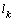 is increased by 275.4%. In this case, for example, for the value
is increased by 275.4%. In this case, for example, for the value 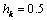 we have
we have 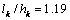 , with increasing
, with increasing 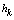 values of this ratio increases, with the largest difference is achieved for values
values of this ratio increases, with the largest difference is achieved for values  and may approach 200%.Thus, the capillarity of the soil increases as the filtration rate, and the width of the strip of irrigated soil. In other words, the capillarity of the soil increases the efficiency of canals and sprinklers of irrigation systems.The last block of table 2 makes it possible to analyze the impact of cross-sectional shape channel power sources, comparing the results for the channels (scheme 1) and sprinklers (scheme 2) with the same filter characteristics. A comparison of these results, as well as from the graphs in scheme 2, it follows that if sprinklers are the final specifications
and may approach 200%.Thus, the capillarity of the soil increases as the filtration rate, and the width of the strip of irrigated soil. In other words, the capillarity of the soil increases the efficiency of canals and sprinklers of irrigation systems.The last block of table 2 makes it possible to analyze the impact of cross-sectional shape channel power sources, comparing the results for the channels (scheme 1) and sprinklers (scheme 2) with the same filter characteristics. A comparison of these results, as well as from the graphs in scheme 2, it follows that if sprinklers are the final specifications 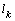 and
and 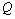 more than in the case of channels, with the difference for these values of 1.4-2.2 and 1.3-1.5 times, respectively.
more than in the case of channels, with the difference for these values of 1.4-2.2 and 1.3-1.5 times, respectively.5. Filtration of the Channels in the Presence of Water Pressure at the Base (Scheme 3).
- As discussed in section 24 schemes 1 and 2, underlying soil layer underlying confined aquifer of high permeability is an important factor, by which the drainage of the soil can be carried out not only with free filtering, but also in the presence of backwater. In those situations where the soil layer is underlain by an impermeable base, the only way to tap filtered water channel is the evaporation from the free surface of ground water. In such cases, naturally raises the question of determining the size of the zone of saturation in the filter channel.In fig. 4 shows the pattern of motion of the channel AB in a layer of soil capacity T, underlain horizontal aquitard FE.
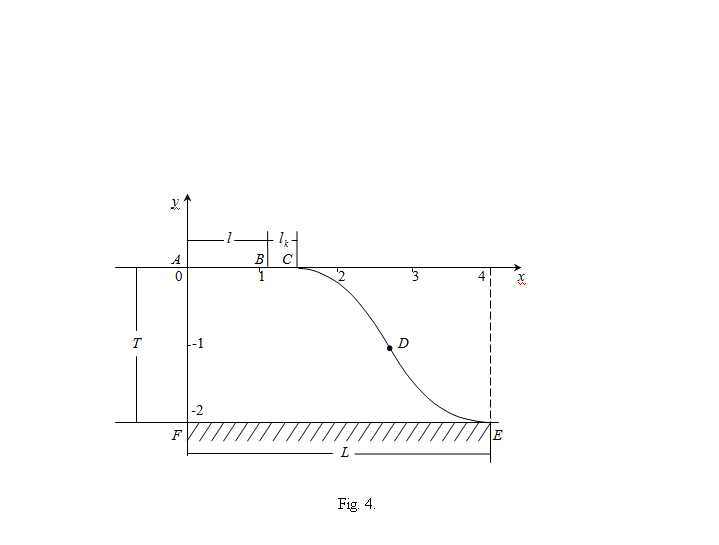 | Figure 4. The flow pattern of the channels with shallow depth of water, based at 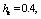 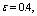 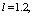 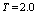 |
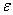 from the free surface CE. In this scheme, the boundary conditions (1) at sites AB, BC, CE, and AF persist, and the boundary conditions FE replaced by the following:
from the free surface CE. In this scheme, the boundary conditions (1) at sites AB, BC, CE, and AF persist, and the boundary conditions FE replaced by the following: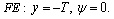 | (8) |
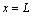 region
region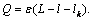 | (9) |
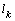 to be finding and also the width of the spreading of water in water-resistant base
to be finding and also the width of the spreading of water in water-resistant base 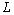 .As an auxiliary parametric variable, it is convenient to choose the previous half-strip plane
.As an auxiliary parametric variable, it is convenient to choose the previous half-strip plane 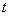 , but with a different line of points
, but with a different line of points 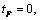
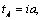
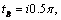
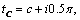
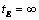 .In this case, the complex velocity field corresponding to the boundary conditions (1), (8), is a circular pentagon with the same incision with apex at point D, but with the two angles at the vertices of E and C, are equal
.In this case, the complex velocity field corresponding to the boundary conditions (1), (8), is a circular pentagon with the same incision with apex at point D, but with the two angles at the vertices of E and C, are equal 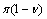 and
and 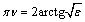 , respectively (fig. 2, b). Function giving a conformal mapping of the parametric variable t in the region
, respectively (fig. 2, b). Function giving a conformal mapping of the parametric variable t in the region 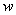 has the form
has the form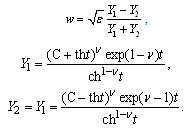 | (10) |
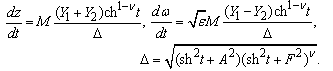 | (11) |
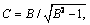
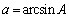 (
(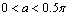 ),
),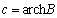 (
(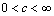 ),
),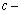 the unknown abscissa of the point
the unknown abscissa of the point 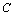 in the plane
in the plane 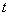 [27 29].To determine the unknown constants of conformal mapping of a, b and M in this case is the system of equations
[27 29].To determine the unknown constants of conformal mapping of a, b and M in this case is the system of equations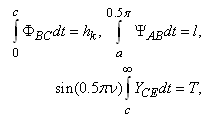 | (12) |
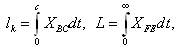 | (13) |
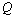 using the formula (9).In the limiting case of motion where there is no soil capillarity, at hk = 0 parameters с = 0, B = 1, C = ∞ and the results obtained[16].In fig. 4 shows the flow pattern of the channel, calculated with
using the formula (9).In the limiting case of motion where there is no soil capillarity, at hk = 0 parameters с = 0, B = 1, C = ∞ and the results obtained[16].In fig. 4 shows the flow pattern of the channel, calculated with 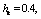
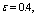
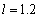 and
and 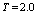 (baseline). In [29, 30] conducted a detailed hydrodynamic analysis of the effect of all the physical characteristics of the circuit 3 on the size of the zone of saturation. We shall therefore examine in more detail by comparing the calculation results obtained in the simulation of circuits 1 and 3. In table 3 (bottom row corresponds to figure 3, and the top - a scheme with the base case
(baseline). In [29, 30] conducted a detailed hydrodynamic analysis of the effect of all the physical characteristics of the circuit 3 on the size of the zone of saturation. We shall therefore examine in more detail by comparing the calculation results obtained in the simulation of circuits 1 and 3. In table 3 (bottom row corresponds to figure 3, and the top - a scheme with the base case 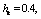
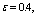
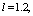
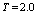 and
and 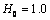 ) the results of numerical calculations of the influence of physical parameters of the model
) the results of numerical calculations of the influence of physical parameters of the model 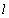 ,
, 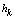 and and the size of the width of the capillary spreading of water
and and the size of the width of the capillary spreading of water 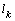 and filtration rate
and filtration rate 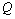 .
.
|
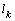 and
and 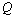 variables,
variables, 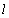 ,
, 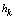 and
and 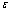 : increasing the channel width, the static height of capillary rise of water, as well as reducing evaporation and bed thickness lead to higher values
: increasing the channel width, the static height of capillary rise of water, as well as reducing evaporation and bed thickness lead to higher values 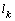 . An increase in the size of the zone of saturation by increasing the spreading of liquid on the water pressure
. An increase in the size of the zone of saturation by increasing the spreading of liquid on the water pressure 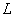 is related to figure 3 to increase capacity of the soil layer, which is quite natural from a physical point of view.The data in table 3 again emphasize the significance of horizontal absorption of water for both schemes 1 and 3: when
is related to figure 3 to increase capacity of the soil layer, which is quite natural from a physical point of view.The data in table 3 again emphasize the significance of horizontal absorption of water for both schemes 1 and 3: when 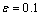 we have
we have 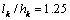 , and this ratio increases with the rate of evaporation
, and this ratio increases with the rate of evaporation 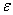 .Comparison with the results of calculations on the previously reviewed [22 24] figure 1 shows that if, for small values of the parameters,
.Comparison with the results of calculations on the previously reviewed [22 24] figure 1 shows that if, for small values of the parameters, 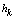 ,
, 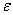 and T and large
and T and large 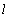 inequalities
inequalities 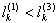 (superscript indicates the calculation of the said schemes 1 and 3), for large values of variable quantities,
(superscript indicates the calculation of the said schemes 1 and 3), for large values of variable quantities, 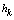 ,
, 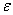 and T and small
and T and small 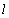 contrary
contrary 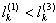 . The greatest difference in the results (72%) was observed when the rate of evaporation.As for consumption, then clearly that
. The greatest difference in the results (72%) was observed when the rate of evaporation.As for consumption, then clearly that 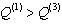 for any parameter values,
for any parameter values, 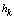 ,
, 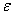 and T. For small and large values of the width of the channels we have, respectively, and inequality
and T. For small and large values of the width of the channels we have, respectively, and inequality 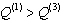 and
and 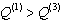 .
.6. Filtration of Water-Filled Channels in the Presence of Water Pressure at the Base (Scheme 4)
- Up to now study the motion of the channels with shallow depth of water. Designed to study the complex analytical scheme 3 (formula (11) (13)) allows us to consider the channels that are filled with water, and thereby estimate the combined effect of the depth of water in canals and evaporation from the free surface of the water table, but in the absence of capillarity, soil, at
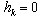 .In fig. 5 shows the flow pattern of the AB channel of rectangular cross section width
.In fig. 5 shows the flow pattern of the AB channel of rectangular cross section width 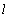 of the water depth
of the water depth 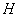 . In this scheme the boundary conditions (1), (8) in areas AF, CE and FE are stored, and the conditions on the segments AB and BC are replaced by these:
. In this scheme the boundary conditions (1), (8) in areas AF, CE and FE are stored, and the conditions on the segments AB and BC are replaced by these: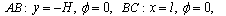 | (14) |
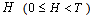 – depth of water in the channel.Taking into account the coincidence of the complex velocity to that of scheme 3 (fig. 2, b) and applying the method P.Y. Polubarinova-Cochina, arrive at a parametric solution (11) with the replacement
– depth of water in the channel.Taking into account the coincidence of the complex velocity to that of scheme 3 (fig. 2, b) and applying the method P.Y. Polubarinova-Cochina, arrive at a parametric solution (11) with the replacement 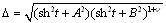 [30]. Expressions (12), (13) for the physical parameters of the model
[30]. Expressions (12), (13) for the physical parameters of the model 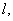
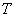 and
and 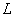 will remain the same, and the first equation (12) takes the following form:
will remain the same, and the first equation (12) takes the following form: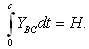 | (15) |
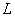 is calculated filtration flow rate
is calculated filtration flow rate 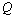 by the formula (9), taking into account the fact that in this scheme
by the formula (9), taking into account the fact that in this scheme 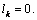 In fig. 5 shows the pattern of motion of the channel, calculated in
In fig. 5 shows the pattern of motion of the channel, calculated in 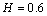 ,
, 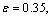
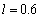 and
and 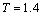 (basic). Hydrodynamic analysis of the effect of all the physical characteristics of the circuit
(basic). Hydrodynamic analysis of the effect of all the physical characteristics of the circuit 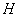 ,
,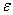 ,
, 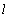 and
and 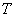 is given in [30]. Below focus on comparing the simulation results for circuits 3 and 4. In table. 4 summarizes the results of calculations of the influence of physical parameters of the scheme on the width of the spreading of water in water-resistant base
is given in [30]. Below focus on comparing the simulation results for circuits 3 and 4. In table. 4 summarizes the results of calculations of the influence of physical parameters of the scheme on the width of the spreading of water in water-resistant base  and consumption
and consumption  .
. 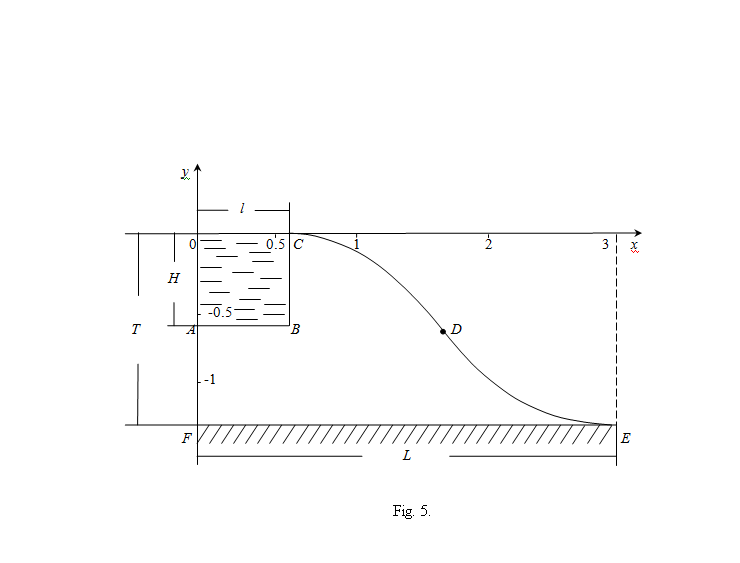 | Figure 5. The flow pattern of channels filled with water, calculated at 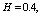 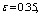 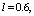 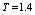 |
|
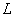 of the channel width
of the channel width 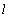 is close to linear, and depending on the quantities
is close to linear, and depending on the quantities 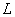 and
and 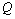 the water level
the water level 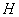 are qualitatively similar if we bear in mind that (9).With regard to flow
are qualitatively similar if we bear in mind that (9).With regard to flow 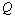 in both schemes, with an increase in performance
in both schemes, with an increase in performance 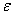 ,
,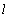 and
and 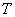 consumption increases, with the largest influence on the reservoir
consumption increases, with the largest influence on the reservoir 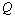 has a capacity
has a capacity 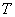 : from table 4 shows that the variation of the parameter
: from table 4 shows that the variation of the parameter 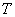 is accompanied by an increase of 313%, ie practically the same as in figure 3.However, in comparison with the scheme 3 biggest changes by varying the layer thickness is undergoing now spreading width of the water: with increasing
is accompanied by an increase of 313%, ie practically the same as in figure 3.However, in comparison with the scheme 3 biggest changes by varying the layer thickness is undergoing now spreading width of the water: with increasing 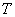 width
width 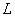 parameter increased by almost 200%.The data in table 4 that the parameter
parameter increased by almost 200%.The data in table 4 that the parameter 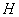 leads to a very small (in the range of 20-30%) deviations of the width of the spreading of water
leads to a very small (in the range of 20-30%) deviations of the width of the spreading of water 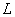 and the seepage flow, so that the influence of water level in the canals of little practical effect on the flow pattern.
and the seepage flow, so that the influence of water level in the canals of little practical effect on the flow pattern.7. Conclusions
- Developed in the computational scheme of filtering channels and sprinklers of irrigation systems in soils underlain silnopronitsaemym confined aquifer or water-resistant base, allow us to make a comparative assessment of the role of cross-sectional shape channel power supply and the water level in it, backwater from the waters of the underlying aquifer or confining layer, soil capillarity and evaporation or seepage at the free surface of the ground water flow pattern.In particular, we establish the following:- compared with the filtration of the sprinklers for irrigators width of the capillary spreading of the liquid and the magnitude of the seepage flow can exceed the corresponding characteristics of more than 50%;- the greatest influence on the width of the capillary spreading of water and filtration rate has capillarity of soil, which improves the efficiency of canals and irrigation canals;- influence the level of water in the channels has practically no effect on the size of the zone of saturation and value of the seepage flow.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML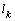 and
and 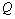 in the variation
in the variation 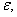
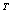 and
and 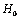 for schemes 1 and 2
for schemes 1 and 2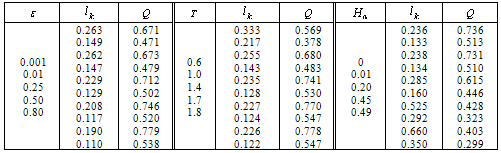
 and the variation
and the variation 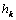 and for circuits 1 and 2
and for circuits 1 and 2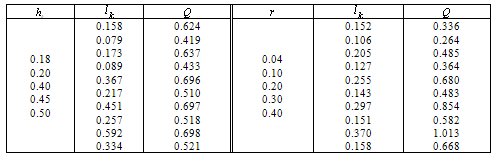
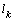 and
and 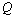 in the variation
in the variation 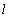
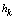 и and
и and 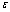 for schemes 1 and 3
for schemes 1 and 3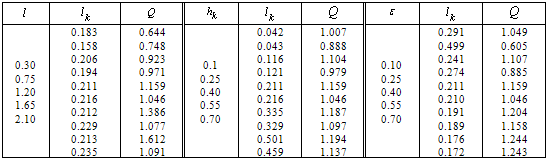
 and
and  in the variation
in the variation 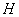
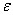 ,
, 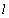 and
and 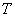 for scheme 4
for scheme 4