-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(2): 112-121
doi: 10.5923/j.am.20110102.19
On the Slow Viscous Flow through a Swarm of Solid Spherical Particles Covered by Porous Shells
Pramod Kumar Yadav
Department of Mathematics, National Institute of Technology Patna, Patna, 800005, Bihar, India
Correspondence to: Pramod Kumar Yadav , Department of Mathematics, National Institute of Technology Patna, Patna, 800005, Bihar, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper concerns the slow viscous flow through a swarm of concentric clusters of porous spherical particles. An aggregate of clusters of porous spherical particles is considered as a hydro-dynamically equivalent to a porous spherical shell enclosing a solid spherical core. The Brinkman equation inside and the Stokes equation outside the porous spherical shell in their stream function formulations are used. As boundary conditions, continuity of velocity, continuity of normal stress and stress-jump condition at the porous and fluid interface, the continuity of velocity components on the solid spherical core are employed. On the hypothetical surface, uniform velocity and Happel boundary conditions are used. The drag force experienced by each porous spherical shell in a cell is evaluated. As a particular case, the drag force experienced by a porous sphere in a cell with jump is also investigated. The earlier results reported for the drag force by Davis and Stone[5] for the drag force experienced by a porous sphere in a cell without jump, Happel[2] for a solid sphere in a cell and Qin and Kaloni[4] for a porous sphere in an unbounded medium have been then deduced. Representative results are presented in graphical form and discussed.
Keywords: Spherical Porous Shell, Cell Model, Permeability, Brinkman Equation, Drag Force
Cite this paper: Pramod Kumar Yadav , "On the Slow Viscous Flow through a Swarm of Solid Spherical Particles Covered by Porous Shells", Applied Mathematics, Vol. 1 No. 2, 2011, pp. 112-121. doi: 10.5923/j.am.20110102.19.
Article Outline
1. Introduction
- The study of viscous flow through a porous medium has gained importance in recent years because of its natural occurrence and of its importance in bio-mechanics, physical sciences and chemical engineering etc. The flow of fluids through a swarm of porous particles has many industrial and engineering applications, such as, in flow through porous beds, in petroleum reservoir rocks, in flow sedimentation, etc. Several researchers have considered the flow of viscous fluid past and through solids or porous bodies with different models. For effective use of a porous medium in the above areas, the structure of porous layer should be viewed from all angles. There are many physical situations arises in which the porous particles moving in the viscous fluid. The flow in most of the above process is creeping because the Reynolds number is smaller than unity. The two terms that play an important role for analytical treatment of the problems related to flow through porous media, are porosity and permeability. The porosity The porosity represents the ratio of volume of openings (voids or pores) to the volume of the material. It seems that more the number of pores, easier will be the flow through the medium, which is not correct and this can be explained by permeability. Permeability is a measureof interconnectivity of voids (pores) in the medium. Hence, its number of voids along with their interconnectivity both that determine the ease with which fluid will flow through the medium. For the medium of high porosity, the sum suggested by Brinkman[1] is more suitable for describing the flow through the porous medium. Brinkman[1] evaluated the viscous force exerted by a flowing fluid on a dense swarm of particles by introducing modified Darcy’s equation for porous medium, which is commonly known as Brinkman equation.In the analysis of flow through swarm of particles, we get cumbersome calculations, if we consider the solution of the flow field over the entire swarm by taking exact positions of the particles. In order to avoid the above complication, it is sufficient to obtain the analytical expression by considering the effects of the neighboring particles on the flow field around a single particle of the swarm, which can be used to develop relatively simple and reliable models for heat and mass transfer. This has lead to the development of particle-in-cell models. Uchida[2] proposed a cell model for a sedimenting swarm of particles, considering spherical particle surrounded by a fluid envelope with cubic outer boundary. This was accurately solved by Brenner[3]. Happel[4, 5] proposed cell models in which both particle and outer envelope are spherical. Happel solved the problem when the inner sphere is solid with respective boundary conditions on the cell surface. The Happel model assumes uniform velocity condition and no tangential stress at the cell surface. The merit of this formulation is that, it leads to an axially symmetric flow that has a simple analytical solution in closed form, and thus can be used for heat and mass transfer calculations. Analytical solutions of particle-in-cell models discussed above are always practically useful to many industrial problems, but the solutions of creeping flow for the above models have not been found in case of complex geometry. However, for geometrically simpler cases like sphere, the analytical solutions were investigated by various authors along with Happel. The problem of the slow viscous flow through an aggregate of concentric clusters of porous cylindrical particles with Happel boundary condition was discussed Deo et al[6]. The drag force experienced by each porous circular cylindrical particle in a cell was evaluated them by using cell model technique Jones[7] had investigated the solution of the problem of Stokes flow past a porous spherical shell. He used Darcy’s law for the porous region and evaluated the drag force experienced by a shell. A Cartesian-tensor solution of the Brinkman equation is investigated by Qin and Kaloni[8] and they also evaluated the drag force on a porous sphere in an unbounded medium. Flow through beds of porous particles was studied by Davis and Stone[9]. They present two approximate models for describing the flow field within a porous particle contained in a fixed or fluidized bed.The first is a swarm model where a spherical porous particle of a specified permeability is contained in a matrix of a different permeability that is equated to the overall bed permeability. The second is a cell model in which the spherical porous particle is placed in a spherical envelope of fluid whose diameter is chosen so that the overall bed porosity is conserved The focus of their work is to derive an expressions for the velocity and pressure profiles inside and outside of the porous particle, to determine the drag force exerted by the flow on a particle, and incorporate the drag information into a macroscopic description of the packed bed of porous particles. Slow extensional flow past a sphere was studied by Bhatt[10]. Stokes flow past a permeable sphere for a non-axi-symmetric case was investigated by Padmavati et al.[11]. Giveler and Altobelli[12] performed experimental measurement of the effective viscosity for the steady flow through a wall bounded by a porous medium and concluded that
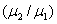 varies from 5.1 to 10.9. Dassios et al.[13] did a celebrated work by finding the solution of Stokes equation in spheroidal coordinates. Later Dassios et al.[14] used the above solution to study the problem of Stokes flow past spheroidal particle-in-cell models with Happel and Kuwabara boundary conditions, which has wide range of applications in problems concerning the flow through swarms of spheroidal particles.Ochoa-Tapia and Whitaker[15, 16] studied the momentum transfer at the boundary between a porous medium and a homogeneous fluid theoretically and experimentally. They develop the appropriate jump condition for momentum transport within the framework of the method of volume averaging and they compare the theory with the experimental studies of Beavers and Joseph[6] and they explore the use of a variable porosity model as a substitute for the jump condition. Many authors have used the stress jump boundary condition in various flow problems and reported significant changes in results. Kuznetsov[17, 18] used the stress jump boundary condition at the fluid-porous interface to discuss flow in channels partially filled with porous medium. The problem of Stokes flow inside a porous spherical shell was solved by Raja-Sekhar and Amarnath[20] by using Darcy’s law for porous outside region and Stokes flow for inside region. The problem of slow extensional bounded flows past a porous sphere whose surface is stretching radially with slip at the surface has been studied by Bhatt and Shirley[21]. Datta and Deo[22] have studied the problem of Stokes flow with slip and Kuwabara boundary conditions and evaluated the drag force experienced by a rigid spheroid in a cell. Viscous flow past a porous sphere with an impermeable core was studied by Bhattacharya and Raja Shekhar[23]. They consider an arbitrary Stokes flow past a porous sphere within an impermeable core and Brinkman’s model is used for the porous medium. The stress jump boundary condition for tangential stresses together with continuity of velocity components and continuity of normal stresses at the permeable boundary are used. They found that the drag and torque not only change with the change of the permeability, but also a significant effect of the stress jump co-efficient is observed. Also, they have used this boundary condition to discuss the arbitrary Stokes flow inside a porous spherical shell[24]. Srivastava and Srivastava[25] studied the Stokes flow through a porous sphere using stress jump condition at the fluid-porous interface and matching Stokes and Oseen’s solutions far away from the sphere. They concluded that drag on a porous sphere decreases with increase of permeability of the medium. Deo and Yadav[26] examined flow past a swarm of porous deformed oblate spheroidal particles with kuwabara boundary condition and evaluated the drag force and studied the effects of deformation parameter on the drag force. Chandesris and Jamet[27] discuss the Boundary conditions at a planar fluid-porous. They have shown that, given a single volume-averaged transport equation in the entire domain (mesoscopic scale), it is possible to solve the problem analytically inside the heterogeneous transition zone using the method of matched asymptotic expansions and thus to analytically derive the boundary conditions that must be applied at the discontinuous interface. This analytical study shows that the stress jump condition is related to the slip velocity but also to the pressure gradient, through two jump parameters. This analysis also provides explicit relations between these two jump parameters and the variations of porosity and permeability in the transition zone through excess quantities. They, also discuss the Boundary conditions at fluid-porous interface[29]. They show that it is possible to provide an explicit relation between the values of jump parameters of the stress jump condition that one should impose at a fluid/porous interface and the structure of the transition region. An explicit relation between the jump parameters, the location of the discontinuous interface (macroscopic description) and the structure of the transition region (mesoscopic description) is obtained. This relation allows to explain the large sensitivity of the jump parameters to the location of the discontinuous interface observed in[27]. Diffusive mass transfer between a microporous medium and an homogeneous fluid was studies by Valdes-Parada et al[28]. They obtain the jump boundary condition between a fluid and a porous medium, for Diffusive and chemical reaction. They, also discuss the Jump momentum boundary condition at a fluid-porous dividing surface[30]. They derived an expression for a jump stress boundary condition free of adjustable coefficient using a method of volume averaging method. The motivations of these papers lead us to discuss the present problem which includes the earlier results for the drag force on a porous sphere.This paper concerns the problem of slow viscous flow through a swarm of clusters of porous spherical particles. As boundary conditions, continuity of velocity, continuity of normal stress and stress-jump condition at the porous and fluid interface, the continuity of velocity components on the solid spherical core are employed. On the hypothetical surface, uniform velocity and Happel boundary conditions are used. The drag force experienced by each porous spherical shell in a cell is evaluated. As a particular case, the drag force experienced by a porous sphere in a cell and in an unbounded medium with jump is also investigated. The earlier results reported for the drag force by Davis and Stone[9] for the drag force experienced by a porous sphere in a cell without jump, Happel[4] for a solid sphere in a cell and Qin and Kaloni[8] for a porous sphere in an unbounded medium have been then deduced.
varies from 5.1 to 10.9. Dassios et al.[13] did a celebrated work by finding the solution of Stokes equation in spheroidal coordinates. Later Dassios et al.[14] used the above solution to study the problem of Stokes flow past spheroidal particle-in-cell models with Happel and Kuwabara boundary conditions, which has wide range of applications in problems concerning the flow through swarms of spheroidal particles.Ochoa-Tapia and Whitaker[15, 16] studied the momentum transfer at the boundary between a porous medium and a homogeneous fluid theoretically and experimentally. They develop the appropriate jump condition for momentum transport within the framework of the method of volume averaging and they compare the theory with the experimental studies of Beavers and Joseph[6] and they explore the use of a variable porosity model as a substitute for the jump condition. Many authors have used the stress jump boundary condition in various flow problems and reported significant changes in results. Kuznetsov[17, 18] used the stress jump boundary condition at the fluid-porous interface to discuss flow in channels partially filled with porous medium. The problem of Stokes flow inside a porous spherical shell was solved by Raja-Sekhar and Amarnath[20] by using Darcy’s law for porous outside region and Stokes flow for inside region. The problem of slow extensional bounded flows past a porous sphere whose surface is stretching radially with slip at the surface has been studied by Bhatt and Shirley[21]. Datta and Deo[22] have studied the problem of Stokes flow with slip and Kuwabara boundary conditions and evaluated the drag force experienced by a rigid spheroid in a cell. Viscous flow past a porous sphere with an impermeable core was studied by Bhattacharya and Raja Shekhar[23]. They consider an arbitrary Stokes flow past a porous sphere within an impermeable core and Brinkman’s model is used for the porous medium. The stress jump boundary condition for tangential stresses together with continuity of velocity components and continuity of normal stresses at the permeable boundary are used. They found that the drag and torque not only change with the change of the permeability, but also a significant effect of the stress jump co-efficient is observed. Also, they have used this boundary condition to discuss the arbitrary Stokes flow inside a porous spherical shell[24]. Srivastava and Srivastava[25] studied the Stokes flow through a porous sphere using stress jump condition at the fluid-porous interface and matching Stokes and Oseen’s solutions far away from the sphere. They concluded that drag on a porous sphere decreases with increase of permeability of the medium. Deo and Yadav[26] examined flow past a swarm of porous deformed oblate spheroidal particles with kuwabara boundary condition and evaluated the drag force and studied the effects of deformation parameter on the drag force. Chandesris and Jamet[27] discuss the Boundary conditions at a planar fluid-porous. They have shown that, given a single volume-averaged transport equation in the entire domain (mesoscopic scale), it is possible to solve the problem analytically inside the heterogeneous transition zone using the method of matched asymptotic expansions and thus to analytically derive the boundary conditions that must be applied at the discontinuous interface. This analytical study shows that the stress jump condition is related to the slip velocity but also to the pressure gradient, through two jump parameters. This analysis also provides explicit relations between these two jump parameters and the variations of porosity and permeability in the transition zone through excess quantities. They, also discuss the Boundary conditions at fluid-porous interface[29]. They show that it is possible to provide an explicit relation between the values of jump parameters of the stress jump condition that one should impose at a fluid/porous interface and the structure of the transition region. An explicit relation between the jump parameters, the location of the discontinuous interface (macroscopic description) and the structure of the transition region (mesoscopic description) is obtained. This relation allows to explain the large sensitivity of the jump parameters to the location of the discontinuous interface observed in[27]. Diffusive mass transfer between a microporous medium and an homogeneous fluid was studies by Valdes-Parada et al[28]. They obtain the jump boundary condition between a fluid and a porous medium, for Diffusive and chemical reaction. They, also discuss the Jump momentum boundary condition at a fluid-porous dividing surface[30]. They derived an expression for a jump stress boundary condition free of adjustable coefficient using a method of volume averaging method. The motivations of these papers lead us to discuss the present problem which includes the earlier results for the drag force on a porous sphere.This paper concerns the problem of slow viscous flow through a swarm of clusters of porous spherical particles. As boundary conditions, continuity of velocity, continuity of normal stress and stress-jump condition at the porous and fluid interface, the continuity of velocity components on the solid spherical core are employed. On the hypothetical surface, uniform velocity and Happel boundary conditions are used. The drag force experienced by each porous spherical shell in a cell is evaluated. As a particular case, the drag force experienced by a porous sphere in a cell and in an unbounded medium with jump is also investigated. The earlier results reported for the drag force by Davis and Stone[9] for the drag force experienced by a porous sphere in a cell without jump, Happel[4] for a solid sphere in a cell and Qin and Kaloni[8] for a porous sphere in an unbounded medium have been then deduced. 2. Statements and Mathematical Formulation of the Problem
- Here we have considered an axi-symmetric Stokes flow of a viscous incompressible fluid through a swarm of porous spherical particles of radius
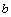 enclosing an impermeable spherical core of radius
enclosing an impermeable spherical core of radius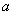 . The above model is equivalent to a co-axial porous spherical shell enclosing the impermeable core. Further, we assume that, this porous shell is enveloped by a concentric sphere of radius
. The above model is equivalent to a co-axial porous spherical shell enclosing the impermeable core. Further, we assume that, this porous shell is enveloped by a concentric sphere of radius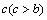 , named as cell surface (Figure-2). The Stokes flow of a Newtonian fluid with absolute fluid viscosity is assumed to be steady and axi-symmetric. Let us consider that porous spherical shells are stationary and steady axi-symmetric viscous flow has been established around and through it by a uniform velocity
, named as cell surface (Figure-2). The Stokes flow of a Newtonian fluid with absolute fluid viscosity is assumed to be steady and axi-symmetric. Let us consider that porous spherical shells are stationary and steady axi-symmetric viscous flow has been established around and through it by a uniform velocity 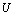 directed in the positive z-axis. The radius
directed in the positive z-axis. The radius 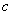 of hypothetical cell is so chosen that the particle volume fraction
of hypothetical cell is so chosen that the particle volume fraction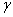 of the swarm is equal to the particle volume fraction of the cell, i.e. relative to this composite sphere (i.e. a core with porous shell) in the hypothetical cell
of the swarm is equal to the particle volume fraction of the cell, i.e. relative to this composite sphere (i.e. a core with porous shell) in the hypothetical cell 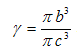 | (1) |
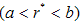 , is governed by the Brinkman[1] equation
, is governed by the Brinkman[1] equation 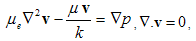 | (2) |
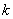 being the permeability of the porous medium,
being the permeability of the porous medium,  and
and 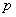 are the velocity vector and pressure at any point in the porous region, respectively. The coefficient
are the velocity vector and pressure at any point in the porous region, respectively. The coefficient  is the effective viscosity for the Brinkman flow which taken to be different from
is the effective viscosity for the Brinkman flow which taken to be different from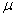 , the viscosity coefficient of clear fluid. The flow in the outside region of the porous spherical shell be governed by the Stokes equation (Happel and Brenner[31]) as
, the viscosity coefficient of clear fluid. The flow in the outside region of the porous spherical shell be governed by the Stokes equation (Happel and Brenner[31]) as 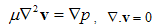 | (3) |
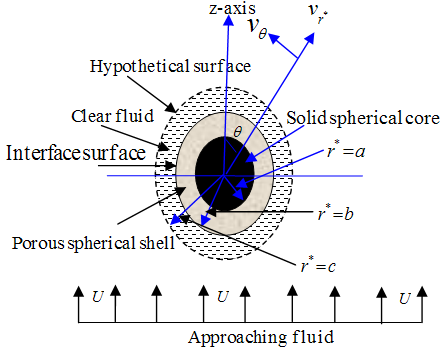 | Figure 2. Physical situation and co-ordinate system of the problem |
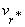 and
and 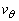 be the velocity components in the direction of
be the velocity components in the direction of 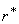 and
and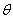 , respectively. Then the Stokes stream function
, respectively. Then the Stokes stream function 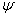 which satisfies equation of continuity in spherical polar coordinates
which satisfies equation of continuity in spherical polar coordinates  can be expressed as
can be expressed as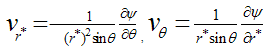 | (4) |
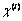 ,
, 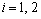 indicates porous and clear fluid regions, respectively. Using the following variables
indicates porous and clear fluid regions, respectively. Using the following variables 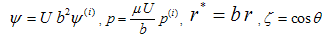 | (5) |
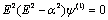 | (6) |
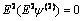 | (7) |
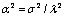 with
with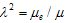 ,
, 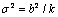 and
and 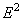 being the dimensionless operator defined by
being the dimensionless operator defined by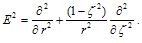 | (8) |
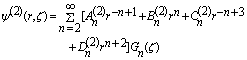 | (9) |
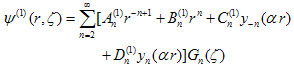 | (10) |
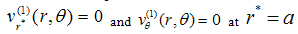 | (11) |
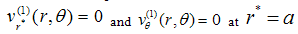 | (12) |
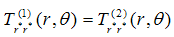 | (13) |
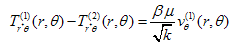 | (14) |
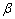 varies in the range -1 to 1 as experimentally found by Ochoa-Tapia and Whitaker[15, 16]. If
varies in the range -1 to 1 as experimentally found by Ochoa-Tapia and Whitaker[15, 16]. If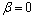 , then we get the continuity of shearing stress. The continuity of the redial components of fluid velocity on the outer cell
, then we get the continuity of shearing stress. The continuity of the redial components of fluid velocity on the outer cell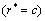 implies:
implies: 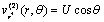 | (15) |
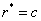 :
: | (16) |
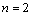 , (Datta and Deo[22]).Therefore, a particular regular solution of the Brinkman equation (6) can be expressed as
, (Datta and Deo[22]).Therefore, a particular regular solution of the Brinkman equation (6) can be expressed as 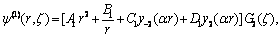 | (17) |
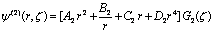 | (18) |
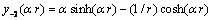
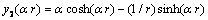 ,
,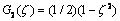 and
and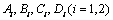 are arbitrary constant which we have to be determined.
are arbitrary constant which we have to be determined.2.1. Determination of Arbitrary Constants
- As a result of application of the boundary conditions (11) – (16) and solving the resulting equations, we get the values of arbitrary constants
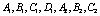 and , which are given in the Appendix A. Thus, all the coefficients have been determined and hence, we get the explicit expressions for stream functions from equations (17) and (18), in both regions.
and , which are given in the Appendix A. Thus, all the coefficients have been determined and hence, we get the explicit expressions for stream functions from equations (17) and (18), in both regions.3. Evaluation of Drag force
- The drag force experienced by each porous spherical shell in a cell can be evaluated by using the simple elegant formula (Happel and Brenner[31], p.-115) as
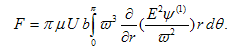 | (19) |
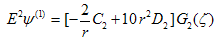 | (20) |
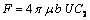 | (21) |
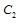 is given in appendix A. Here, it may be noted that Stokeslet coefficient
is given in appendix A. Here, it may be noted that Stokeslet coefficient 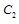 of the stream function only contribute to the drag force.Also, the drag coefficient
of the stream function only contribute to the drag force.Also, the drag coefficient 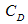 can be defined as
can be defined as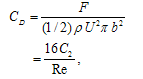 | (22) |
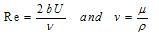 being the Reynolds number and kinematic viscosity of fluid, respectively.When hypothetical cell radius
being the Reynolds number and kinematic viscosity of fluid, respectively.When hypothetical cell radius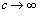 i.e.,
i.e., 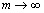 , then the porous spherical shell lies in an unbounded medium. In this case, the value of the drag force comes out as
, then the porous spherical shell lies in an unbounded medium. In this case, the value of the drag force comes out as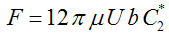 | (23) |
 is given in Appendix B. This is a new result reported for the drag force experienced by a porous spherical shell in an unbounded medium with jump condition.In the limit of
is given in Appendix B. This is a new result reported for the drag force experienced by a porous spherical shell in an unbounded medium with jump condition.In the limit of 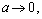 i.e.,
i.e., 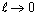 , the porous spherical shell reduces to the porous sphere in a cell. Therefore, the value of drag force
, the porous spherical shell reduces to the porous sphere in a cell. Therefore, the value of drag force 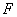 experienced by the porous sphere of radius
experienced by the porous sphere of radius 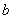 comes out as
comes out as 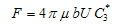 | (24) |
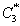 is given in Appendix BThis is also a new result reported for the drag force experienced by a porous sphere in a cell with jump condition.Also, in the limit
is given in Appendix BThis is also a new result reported for the drag force experienced by a porous sphere in a cell with jump condition.Also, in the limit 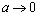 i.e.,
i.e.,  and
and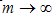 , the physical problems corresponds to the porous sphere of radius
, the physical problems corresponds to the porous sphere of radius 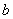 in unbounded medium. In this case, the value of drag force
in unbounded medium. In this case, the value of drag force 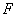 experienced by a porous sphere comes out as
experienced by a porous sphere comes out as | (25) |
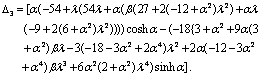 | (26) |
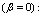 If
If , i.e.,
, i.e.,  , then the porous spherical shell reduces to the porous sphere of radius
, then the porous spherical shell reduces to the porous sphere of radius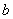 . In this case, the value of drag force
. In this case, the value of drag force 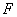 experienced by a porous sphere for the case of
experienced by a porous sphere for the case of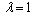 comes out as
comes out as 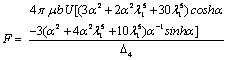 | (27) |
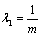 | (28) |
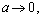 i.e.,
i.e., 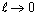 and
and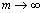 , then the porous spherical shell reduces to the porous sphere in an unbounded medium. In this case, the value of drag force
, then the porous spherical shell reduces to the porous sphere in an unbounded medium. In this case, the value of drag force 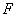 experienced by a porous sphere of radius for the case ofturns out as
experienced by a porous sphere of radius for the case ofturns out as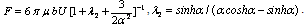 | (29) |
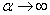 , reduces to
, reduces to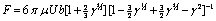 | (30) |
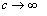 i.e.
i.e. 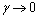 , then from equation (30), the drag force experienced by solid sphere of radius
, then from equation (30), the drag force experienced by solid sphere of radius 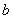 in an unbounded medium is comes out as
in an unbounded medium is comes out as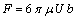 | (31) |
4. Results and Discussions
- In this study, the drag force experienced by a porous spherical shell in a cell, porous spherical shell in an unbounded medium, porous sphere in a cell and porous sphere in an unbounded medium with jump are evaluated. The dependence of the drag coefficient
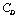 on various parameters like permeability parameter
on various parameters like permeability parameter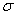 , viscosity ratio
, viscosity ratio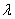 , particle volume fraction
, particle volume fraction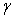 , porosity parameter
, porosity parameter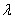 and jump coefficient
and jump coefficient 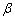 are discussed. The variation of
are discussed. The variation of 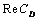 versus particle volume fraction
versus particle volume fraction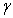 and permeability parameter
and permeability parameter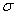 for the porous spherical shell is shown in Fig.-3. It is observed that
for the porous spherical shell is shown in Fig.-3. It is observed that 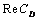 slightly increases with increase in permeability parameter
slightly increases with increase in permeability parameter 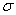 for low values of particle volume fraction
for low values of particle volume fraction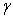
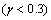 as for small values of
as for small values of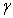 the flow around a shell is not influenced very much by neighbouring particles. However, for large values of particle volume fraction
the flow around a shell is not influenced very much by neighbouring particles. However, for large values of particle volume fraction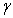
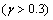 a significant increase in
a significant increase in 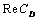 is observed with
is observed with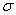 except for very low values of permeability parameter
except for very low values of permeability parameter
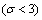 .
. | Figure 3. Variation of ReCD versus particle volume fraction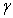 and permeability parameter for the porous spherical shell when porosity parameter and permeability parameter for the porous spherical shell when porosity parameter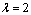 , jump coefficient , jump coefficient 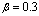 and and 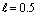 |
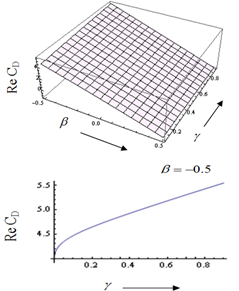
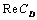 on permeability parameter
on permeability parameter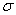 and jump coefficient
and jump coefficient 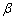 is shown in Fig.-4. For all values of jump coefficient
is shown in Fig.-4. For all values of jump coefficient 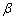 ,
, 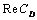 asymptotically increases with increase of permeability parameter
asymptotically increases with increase of permeability parameter 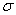 . However,
. However, 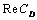 gradually decreases with increase in jump coefficient
gradually decreases with increase in jump coefficient 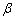 for small values of permeability parameter
for small values of permeability parameter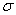 and for large values of
and for large values of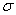 ,
, 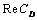 asymptotically decreases. For all values of jump coefficient
asymptotically decreases. For all values of jump coefficient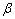 ,
, 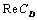 increases with particle volume fraction
increases with particle volume fraction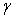 (Fig.-5). It is also fined out that
(Fig.-5). It is also fined out that 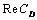 gradually decreases with increase in jump coefficient
gradually decreases with increase in jump coefficient 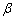 for all values of
for all values of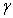 . It clearly indicates that the variation of
. It clearly indicates that the variation of 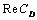 with particle volume fraction
with particle volume fraction is independent of the shearing stress in the clear fluid relative to the shearing stress in the porous region at the fluid-porous interface. Here, as
is independent of the shearing stress in the clear fluid relative to the shearing stress in the porous region at the fluid-porous interface. Here, as 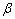 increases the value of
increases the value of 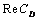 decreases. Hence, it is felt that there is a significant effect of the stress jump coefficient
decreases. Hence, it is felt that there is a significant effect of the stress jump coefficient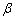 on the flow like volume flow, drag force etc. Therefore while studying viscous flow problems involving Stokes equation in clear fluid region and Brinkman equation in porous media; one has to take the stress jump in the tangential stress components into consideration, which has a significant impact on the physical problem. Also, this helps us to estimate the flow quantities more accurately and to realize the dependency of the physical problem on the boundary conditions.
on the flow like volume flow, drag force etc. Therefore while studying viscous flow problems involving Stokes equation in clear fluid region and Brinkman equation in porous media; one has to take the stress jump in the tangential stress components into consideration, which has a significant impact on the physical problem. Also, this helps us to estimate the flow quantities more accurately and to realize the dependency of the physical problem on the boundary conditions.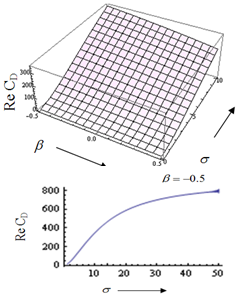 | Figure 4. Variation of ReCD versus jump coefficient  and permeability parameter and permeability parameter  for the porous spherical shell when porosity parameter for the porous spherical shell when porosity parameter , particle volume fraction , particle volume fraction 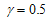 and and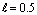 |
 | Figure 5. Variation of ReCD versus jump coefficient 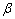 and particle volume fraction for the porous spherical shell when porosity parameter and particle volume fraction for the porous spherical shell when porosity parameter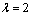 , permeability parameter , permeability parameter and and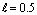 |
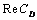 with particle volume fraction
with particle volume fraction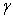 and porosity parameter
and porosity parameter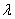 is shown in Fig.-6. We observe that
is shown in Fig.-6. We observe that 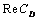 decreases with increase in particle volume fraction
decreases with increase in particle volume fraction 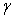 for small porosity parameter
for small porosity parameter 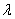
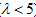 .As the porosity parameter increases
.As the porosity parameter increases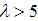 ,
, 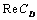 significantly increases to an asymptotic value with particle volume fraction. Evidently, we conclude that higher the effective viscosity in the porous medium comparative to the viscosity of the clear fluid, higher will be the rate of increase of drag force with particle volume fraction
significantly increases to an asymptotic value with particle volume fraction. Evidently, we conclude that higher the effective viscosity in the porous medium comparative to the viscosity of the clear fluid, higher will be the rate of increase of drag force with particle volume fraction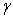 at the fluid-porous interface.
at the fluid-porous interface. 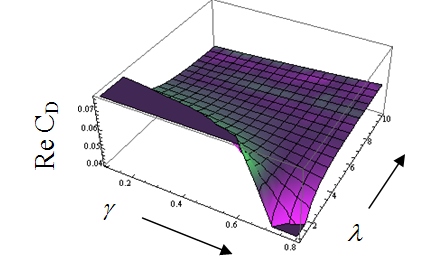 | Figure 6. Variation of ReCD versus porosity parameterand particle volume fraction for the porous spherical shell when jump coefficient, permeability parameter and |
 on porosity parameter
on porosity parameter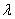 and permeability parameter
and permeability parameter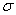 is shown. The term
is shown. The term  increases to an asymptotic value with permeability parameter
increases to an asymptotic value with permeability parameter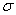 . For all values of permeability parameter
. For all values of permeability parameter 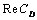 first increases rapidly with porosity parameter
first increases rapidly with porosity parameter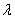 and then become steady. Here the numerical results and figures for given input values have been evaluated through Mathematica software.
and then become steady. Here the numerical results and figures for given input values have been evaluated through Mathematica software. 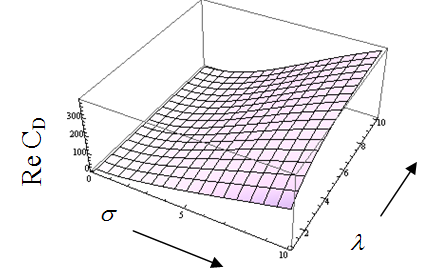 | Figure 7. Variation of ReCD versus porosity parameter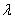 and permeability parameter and permeability parameter 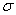 for the porous spherical shell when jump coefficient for the porous spherical shell when jump coefficient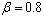 , particle volume fraction , particle volume fraction 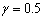 and and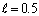 |
Appendix A
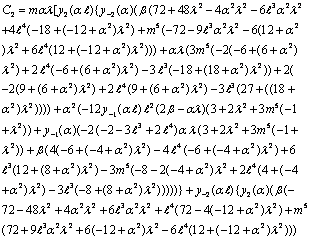

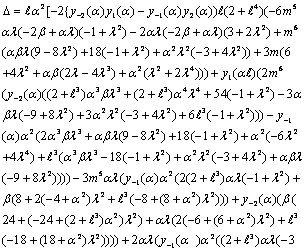
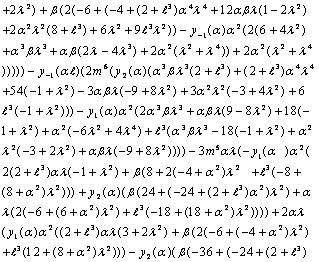

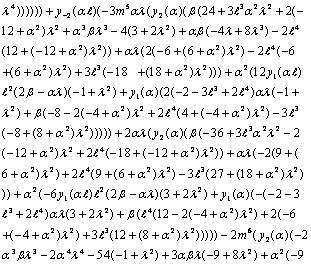
 where,
where, 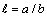 and
and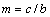 , are dimensionless parameters with
, are dimensionless parameters with 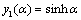 and
and 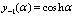
Appendix B
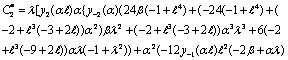





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML