| [1] | N. M. Krylov and N. N. Bogoliubov, Introduction to nonlinear mechanics. Princeton, Princeton University Press, 1947 |
| [2] | N. N. Bogoliubov and Yu. A. Mitropolsky, Asymptotic methods in the theory of non-linear oscillations. New York, Gordon and Breach, 1961 |
| [3] | Th. J. Coakley, A Generalized Averaging Method for Linear Differential Equations with Almost Periodic Coefficients. National Aeronautics and Space Administration, Washington, D. C., 1969 |
| [4] | Ju. A. Mitropolsky, Method of an average in the nonlinear mechanics. Kiev, Naukova dumka, 1971 |
| [5] | J. A. Sanders and F. Verhulst, Averaging methods in nonlinear dynamical systems. Appl. Math. Sci., Springer-Verlag, New York, 1985, vol. 59 |
| [6] | V. M. Volosov and B. I. Morgunov, Metod of average in the theory of nonlinear oscillations. Мoscow, Moscow State University Publishing house, 1971 |
| [7] | P. Lochak, C. Meunier, Multiphase averaging for classical systems. Appl. Math. Sci., Springer-Verlag, New York, 1988, vol. 72 |
| [8] | N. A. Perestyuk, V. A. Plotnikov, A. M. Samoilenko and N. V. Skripnik, Differential equations with impulse effects: multivalued right-hand sides with discontinuities. De Gruyter Studies in Mathematics. Berlin/Boston: Walter De Gruyter GmbH\&Co., 2011, vol. 40 |
| [9] | A. V. Plotnikov and N. V. Skripnik, Differential equations with ''clear'' and fuzzy multivalued right-hand sides. Asymptotics Methods. AstroPrint, Odessa, 2009 |
| [10] | V. A. Plotnikov, A. V. Plotnikov and A. N. Vityuk, Differential equations with a multivalued right-hand side: Asymptotic methods. AstroPrint, Odessa, 1999 |
| [11] | L. Ambrosio and L. Tilli, Topics on analysis in metric spaces. Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, Oxford, 2004, vol. 25 |
| [12] | V. Lakshmikantham, T. Granna Bhaskar and J. Vasundhara Devi, Theory of set differential equations in metric spaces. Cambridge Scientific Publishers. 2006 |
| [13] | V. Lakshmikantham and R. N. Mohapatra, Theory of Fuzzy Differential Equations and Inclusions. London, Taylor & Francis, 2003 |
| [14] | Plotnikov, A.V. and Skripnik, N.V., 2011, Set-valued differential equations with generalized derivative., J. Advanced Research in Pure Mathematics, 13(1), 144-160 |
| [15] | de Blasi, F. S. and Iervolino, F., 1969, Equazioni differentiali con soluzioni a valore compatto convesso., Boll. Unione Mat. Ital., 2(4-5), 491-501 |
| [16] | Bede, B. and Stefanini, L., 2008, Generalized Hukuhara differentiability of interval-valued functions and interval differential equations., Univ. Urbino ''Carlo Bo'', Working Paper Series in Economics, Math. and Statistics. WP-EMS#2008/03 |
| [17] | de Blasi, F. S. and Iervolino, F., 1971, Euler method for differential equations with set-valued solutions., Boll. Unione Mat. Ital., 4(4), 941-949 |
| [18] | Brandao Lopes Pinto, A. J., de Blasi, F. S. and Iervolino, F., 1970, Uniqueness and existence theorems for differential equations with compact convex valued solutions., Boll. Unione Mat. Ital., (4), 534-538 |
| [19] | Dabrowska, R.. and Janiak, T., 1993, Stability of functional- differential equations with compact convex valued solutions., Discuss. Math., (13), 87-92 |
| [20] | Drici, Z., Mcrae, F. A. and Vasundhara Devi, J., 2005, Set differential equations with causal operators., Mathematical Problems in Engineering, 2005:2, 185–194 |
| [21] | Galanis, G. N., Gnana Bhaskar, T., Lakshmikantham, V., and Palamides, P. K., 2005, Set value functions in Frechet spaces: Continuity, Hukuhara differentiability and applications to set differential equations., J. Nonlinear Analysis, 61, 559-575 |
| [22] | Galanis, G. N., Tenali, G. B. and Lakshmikantham, V., 2008, Set differential equations in Frechet spaces., J. Appl. Anal., 14, 103-113 |
| [23] | Gnana Bhaskar, T. and Lakshmikantham, V., 2003, Set differential equations and flow invariance., Appl. Anal. (82), 357-368 |
| [24] | Gnana Bhaskar, T. and Lakshmikantham, V., 2004, Lyapunov stability for set differential equations., Dynam. Systems Appl., (13), 1-10 |
| [25] | Gnana Blaskar, T. and Vasundhara Devi, J., 2005, Set differential systems and vector Lyapunov functions., Appl. Math. Comput., 165(3), 539-548 |
| [26] | Kisielewicz, M., 1975, Description of a class of differential equations with set-valued solutions., Lincei-Rend. Sc. fis. mat. e nat., 58, 158-162 |
| [27] | Kisielewicz, M., Serafin, B. and Sosulski, W., 1975, Existence theorem for functional-differential equation with compact convex valued solutions., Demonstratio math., 13(2), 229-237 |
| [28] | Komleva, T. A., Plotnikov, A. V. and Skripnik, N. V., 2008, Differential equations with set-valued solutions., Ukr. Math. J., 60(10), 1540-1556 |
| [29] | Lakshmikantham, V., 2004, The connection between set and fuzzy differential equations., Facta Univ. Ser. Mech. Automat. Control. Robot., 4, 1-10 |
| [30] | Lakshmikantham, V., 2005, Set differential equations versus fuzzy differential equations., J. Applied Mathematics and Computation, 164, 277-294 |
| [31] | Laksmikantham, V., Leela, S. and Vatsala, A. S., 2002, Setvalued hybrid differential equations and stability in terms of two measures., J. Hybrid Systems, (2), 169-187 |
| [32] | Laksmikantham, V., Leela, S. and Vatsala, A. S., 2003, Interconnection between set and fuzzy differential equations., Nonlinear Anal., 54, 351-360 |
| [33] | Lakshmikantham, V. and Tolstonogov, A. A., 2003, Existence and interrelation between set and fuzzy differential equations., Nonlinear Anal., 55, 255-268 |
| [34] | Piszczek, M., 2006, Second Hukuhara derivative and cosine family of linear set-valued functions., An. Acad. Paedagogicae Cracoviensis. Studia Math., 33, 87-98 |
| [35] | Piszczek, M., 2008, On a multivalued second order differential problem with Hukuhara derivative., Opuscula Math., 28(2), 151-161 |
| [36] | Plotnikov, A. V., 2000, Differentiation of multivalued mappings. T-derivative., Ukr. Math. J., 52(8), 1282-1291 |
| [37] | Plotnikov, A. V. and Tumbrukaki, A. V., 2000, Integro-differential equations with multivalued solutions., Ukr. Math. J., 52(3), 413-423 |
| [38] | Plotnikova, N. V., 2006, Approximation of a set of solutions of linear differential inclusions., Nonlinear Oscil., 9(3), 375-390 |
| [39] | Skripnik, N. V., 2008, The Krasnoselskii-Krein theorem for differential equations with multivalued solutions., Visn. Khark. Univ., Ser. Mat. Prykl. Mat. Mekh., 826(58), 87-99 |
| [40] | Smajdor, A., 2003, On a multivalued differential problem., Internat. J. Bifur. Chaos Appl. Sci. Engrg., 13, 1877-1882 |
| [41] | Tise, I., 2007, Data dependence of the solutions for set differential equations., Carpathian J. Math., 23(1-2), 192-195 |
| [42] | A. Tolstonogov, Differential inclusions in a Banach space, Dordrecht, Kluwer Academic Publishers, 2000 |
| [43] | Vityuk, A. N., 2003, Differential equations of fractional order with set-valued solutions., Visn. Odes. Derzh. Univ., Ser. Fiz.-Mat. Nauky., 8(2), 108-112 |
| [44] | Ahmad, B. and Sivasundaram, S., 2008, -stability of impulsive hybrid setvalued differential equations with delay by perturbing lyapunov functions., Communications in Applied Analysis, 12(2), 137-146 |
| [45] | Arsirii, A. V. and Plotnikov, A. V., 2009, Systems of control over set-valued trajectories with terminal quality criterion., Ukr. Math. J., 61(8), 1349-1356 |
| [46] | N. D. Phu and T. T. Tung, Multivalued Differential Equations, VNU - HCM City: Publishing House, 2005 |
| [47] | Phu, N. D. and Tung, T. T., 2007, Existence of solutions of set control differential equations., J. Sci. Tech. Devel., 10(6), 5-14 |
| [48] | A. V. Plotnikov, “Differential inclusions with Hukuhara derivative and some control problems,” Rep. VINITI 26.04.82, 2036-82, 1982 |
| [49] | Janiak, T. and Łuczak-Kumorek, E., 2003, Method on partial averaging for functional-differential equations with Hukuhara's derivative. Studia Univ. ''Babeş-Bolyai'', Math., XLVIII(2), 65-72 |
| [50] | Kichmarenko, O. D., 2009, Averaging of differential equations with Hukuhara derivative with maxima., Int. J. Pure Appl. Math., 57(3), 447-457 |
| [51] | Kisielewicz, M., 1976, Method of Averaging for Differential Equations with Compact Convex Valued Solutions., Rend. Math., 9(3), 397-408 |
| [52] | Plotnikov, V. A. and Kichmarenko, O. D., 2006, Averaging of controlled equations with the Hukuhara derivative., Nonlinear Oscil., 9(3), 365-374 |
| [53] | Plotnikov, V. A. and Rashkov, P. I., Averaging in differential equations with Hukuhara derivative and delay., Funct. Differ. Equ., (8), 371-381 |
| [54] | Radstrom, H, 1952, An embeldding theorem for spaces of convex sets., Proc. Amer. Math. Soc., (3), 165-169 |
| [55] | Hukuhara, M., 1967, Integration des applications mesurables dont la valeur est un compact convexe., Funkcial. Ekvac., (10), 205-223 |

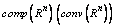 be a set of all nonempty (convex) compact subsets from the space
be a set of all nonempty (convex) compact subsets from the space 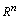 ,
,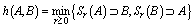 be Hausdorff distance between sets
be Hausdorff distance between sets 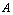 and
and 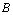 ,
, 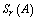 is
is 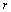 -neighborhood of set
-neighborhood of set 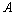 .Let
.Let 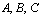 be in
be in 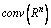 . The set
. The set 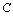 is the Hukuhara difference of
is the Hukuhara difference of 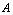 and
and 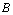 , if
, if 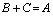 , i.e.
, i.e. 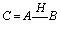 From Radstrom's Cancellation Lemma[54], it follows that if this difference exists, then it is unique.Definition[55]. A mapping
From Radstrom's Cancellation Lemma[54], it follows that if this difference exists, then it is unique.Definition[55]. A mapping 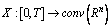 is differentiable in the sense of Hukuhara at
is differentiable in the sense of Hukuhara at 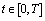 if for some
if for some 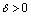 the Hukuhara differences
the Hukuhara differences 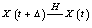 ,
, 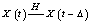 exists in
exists in 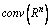 for all
for all 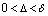 and there exists an
and there exists an 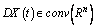 such that
such that 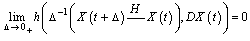 and
and 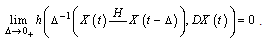 Here
Here 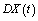 is called the Hukuhara derivative of
is called the Hukuhara derivative of 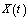 at
at 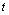 .
.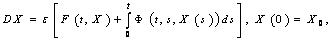
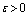 is a small parameter,
is a small parameter, 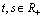 ,
,  is a multivalued mapping,
is a multivalued mapping, 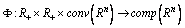 is a multivalued mapping, Here the integral is understood in the sense of[55] (the integral exists for example if
is a multivalued mapping, Here the integral is understood in the sense of[55] (the integral exists for example if 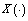 is measurable and the real mapping
is measurable and the real mapping 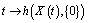 is integrable on
is integrable on  ),
), 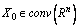 .Definition. A mapping
.Definition. A mapping 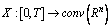 is a solution to the problem (1) if and only if it is continuous and satisfies the integral equation
is a solution to the problem (1) if and only if it is continuous and satisfies the integral equation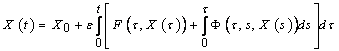 for all
for all 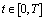 .In this section we associate with the equation (1) the following averaged integrodifferential equation
.In this section we associate with the equation (1) the following averaged integrodifferential equation
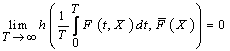
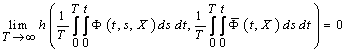
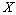 , if for any
, if for any 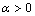 and any
and any 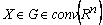 there exists
there exists 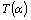 such that
such that 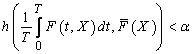 ,
,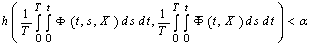 .for all
.for all 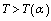 .Theorem. Let in domain
.Theorem. Let in domain 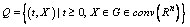 the following hold:1)
the following hold:1)  is continuous in
is continuous in 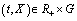 ;2)
;2) 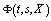 is continuous in
is continuous in 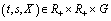 ;3) there exist continuous functions
;3) there exist continuous functions 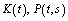 , and constants
, and constants 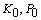 such that
such that 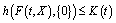 ,
, 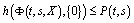 ,
,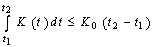 ,
, 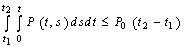 for any
for any 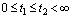 ;4) there exist continuous functions
;4) there exist continuous functions 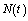 ,
, 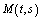 , and constants
, and constants 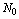 ,
, 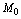 ,
, 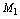 such that
such that 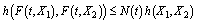 ,
,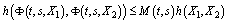 ,
,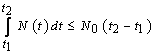 ,
, 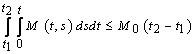 ,
, 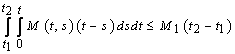 for any
for any 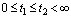 ;5) there exist continuous function
;5) there exist continuous function 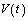 , and constants
, and constants 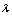 ,
, 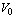 ,
, 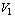 such that
such that 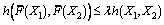 ,
,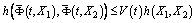 ,
,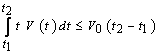 ,
, 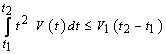 for any
for any 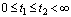 ;6) the limits (3),(4) exist uniformly in
;6) the limits (3),(4) exist uniformly in 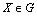 ;7) for any
;7) for any 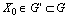 and
and 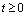 the solution of the equation (2) together with a
the solution of the equation (2) together with a 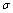 -neighborhood belong to the domain
-neighborhood belong to the domain 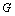 .Then for any
.Then for any 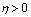 and
and 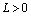 there exists
there exists 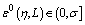 such that for all
such that for all 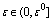 and
and 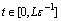 the following statement fulfill:
the following statement fulfill: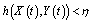
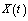 ,
, 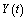 are the solutions of the initial and the averaged equations.Proof. Since
are the solutions of the initial and the averaged equations.Proof. Since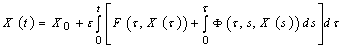 ,
, we have
we have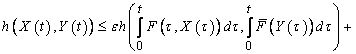
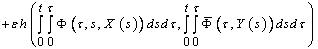 .Hence
.Hence
 into partial intervals by the points
into partial intervals by the points 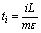 ,
, 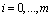 ,
, 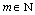 .Then
.Then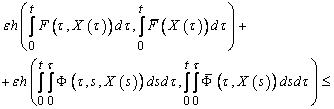
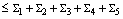 ,where
,where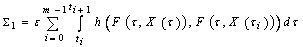 ,
,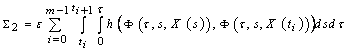 ,
,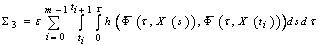
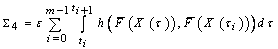 ,
,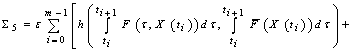
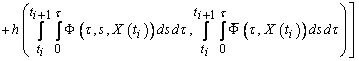 .By condition 3) of the theorem, we get
.By condition 3) of the theorem, we get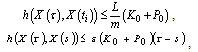
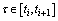 .From (7), and conditions of the theorem, we have
.From (7), and conditions of the theorem, we have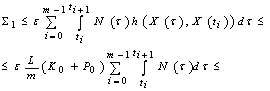
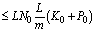 ,
,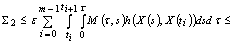
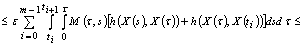
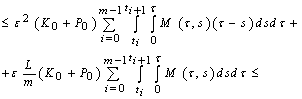
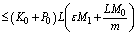 ,
,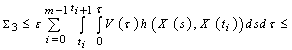
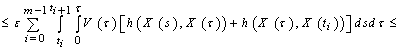
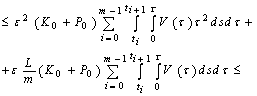
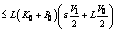 ,
,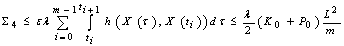 .Hence, for any
.Hence, for any 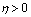 , there exist
, there exist 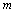 , and
, and 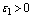 such that the following estimate is true for
such that the following estimate is true for 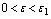 :
:
 and
and  such that1)
such that1)  ,
, 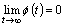 ;2)
;2) 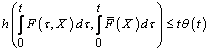 ,
,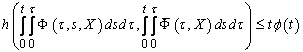 .Then
.Then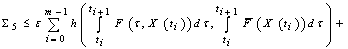
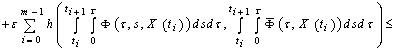

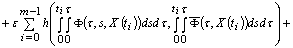
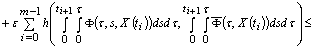
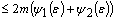 ,where
,where 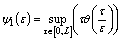 ,
, 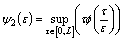 ,
, 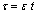 .Fix
.Fix 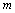 . Then for any
. Then for any 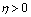 , there exists
, there exists 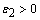 such that the following estimate is true for
such that the following estimate is true for 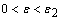 :
: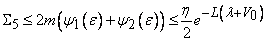
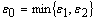 . Combining (6), (8), and (9), we obtain
. Combining (6), (8), and (9), we obtain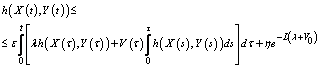 Using Gronwall-Bellman's inequality, we obtain
Using Gronwall-Bellman's inequality, we obtain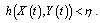 This concludes the proof.
This concludes the proof.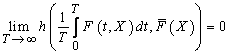
 the following hold:1)
the following hold:1)  is continuous in
is continuous in  ;2)
;2) 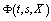 is continuous in
is continuous in 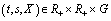 ;3) there exist continuous functions
;3) there exist continuous functions 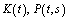 , and constants
, and constants 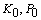 such that
such that 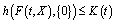 ,
, 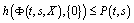 ,
,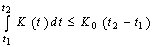 ,
, 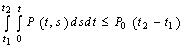 for any
for any 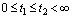 ;4) there exist continuous functions , , and constants , , such that , ,, , for any ;5) there exist continuous function
;4) there exist continuous functions , , and constants , , such that , ,, , for any ;5) there exist continuous function 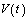 , and constants
, and constants 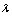 ,
, 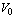 ,
, 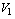 such that
such that 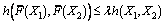 ,
,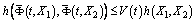 ,
,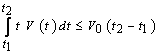 ,
, 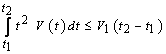 for any
for any 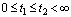 ;6) the limits (3),(4) exist uniformly in
;6) the limits (3),(4) exist uniformly in 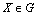 ;7) for any
;7) for any 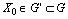 and
and 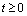 the solution of the equation (2) together with a
the solution of the equation (2) together with a 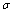 -neighborhood belong to the domain
-neighborhood belong to the domain 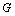 .Then for any
.Then for any 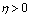 and
and 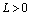 there exists
there exists 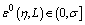 such that for all
such that for all 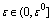 and
and 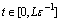 the following statement fulfill:
the following statement fulfill: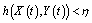 where
where 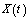 ,
, 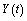 are the solutions of the initial and the averaged equations.Proof. Since
are the solutions of the initial and the averaged equations.Proof. Since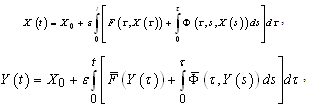 we have
we have 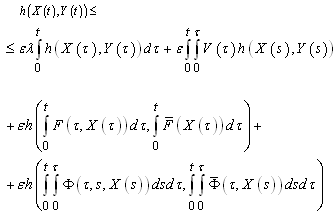
 into partial intervals by the points
into partial intervals by the points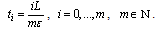 Then
Then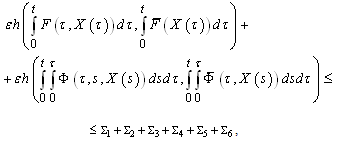 where
where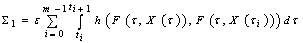 ,
,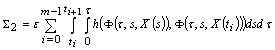 ,
,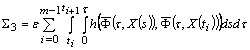 ,
,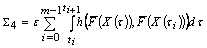 ,
,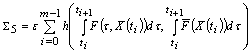 ,
,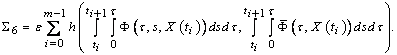 By condition 3) of the theorem, we get
By condition 3) of the theorem, we get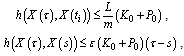
 From (13), and conditions of the theorem, we have
From (13), and conditions of the theorem, we have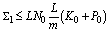 ,
, 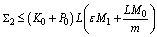 ,
,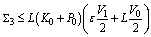 ,
,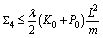 .Hence, for any
.Hence, for any 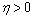 , there exist
, there exist 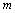 , and
, and 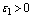 such that the following estimate is true for
such that the following estimate is true for 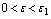 :
: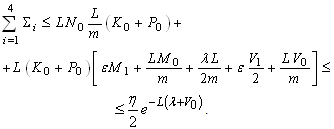
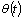 such that1)
such that1) 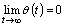 ;2)
;2) 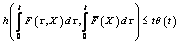 .Then
.Then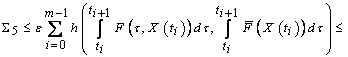

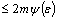 ,where
,where 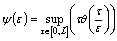 ,
, 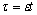 .Fix
.Fix 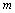 . Then for any
. Then for any 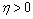 , there exists
, there exists 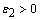 such that the following estimate is true for
such that the following estimate is true for 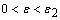 :
: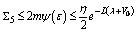
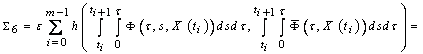
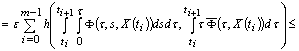
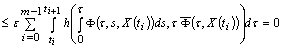 .Now, we get
.Now, we get  . Combining (12), (14), and (15), we obtain
. Combining (12), (14), and (15), we obtain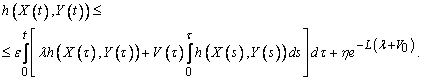 Using Gronwall-Bellman's inequality, we obtain
Using Gronwall-Bellman's inequality, we obtain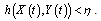 This concludes the proof.
This concludes the proof. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML