-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(2): 87-89
doi: 10.5923/j.am.20110102.14
The Domain of the Fourier Integral
V. N. Tibabishev
Lugansk, Ukraine
Correspondence to: V. N. Tibabishev , Lugansk, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We consider the problem of determining the Fourier integral in the Hilbert space of square integrable functions. Fourier integral is the scalar product of two functions belonging to the Hilbert space of square integrable functions and the Hilbert space of almost periodic functions. Scalar product for different Hilbert spaces defined at the intersection of these spaces, which contains only one zero element. Therefore, the Fourier integral is not defined in the Hilbert space of square integrable functions with nonzero norm.
Keywords:
Cite this paper: V. N. Tibabishev , "The Domain of the Fourier Integral", Applied Mathematics, Vol. 1 No. 2, 2011, pp. 87-89. doi: 10.5923/j.am.20110102.14.
Article Outline
1. Introduction
- In automatic control theory has found wide application of the Fourier integral. Known[1] that the Fourier integral is defined in the space of absolutely integrable functions on the whole line
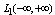 and in the Hilbert space of square integrable functions on the whole line
and in the Hilbert space of square integrable functions on the whole line 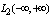 . The functions performed by the Fourier integral, is interpreted as an infinite sum of harmonic oscillations with infinitely close frequencies and with an infinitely small amplitudes[2]. In addition, in a Hilbert space
. The functions performed by the Fourier integral, is interpreted as an infinite sum of harmonic oscillations with infinitely close frequencies and with an infinitely small amplitudes[2]. In addition, in a Hilbert space 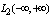 there exists an orthonormal system of functions, such as Hermite[1]. In this case, the same element of the Hilbert space
there exists an orthonormal system of functions, such as Hermite[1]. In this case, the same element of the Hilbert space 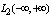 can be represented not only by the Fourier integral, but also a Fourier series in the orthonormal system, for example, the Hermite functions. Dual representation of one element belonging to the same Hilbert space, leads to contradictions. In the representation of the Fourier space element is interpreted by a countably infinite sum of projections of a countable orthonormal basis
can be represented not only by the Fourier integral, but also a Fourier series in the orthonormal system, for example, the Hermite functions. Dual representation of one element belonging to the same Hilbert space, leads to contradictions. In the representation of the Fourier space element is interpreted by a countably infinite sum of projections of a countable orthonormal basis 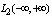 . In the representation of the Fourier integral, the same element in the same space is interpreted by an uncountable amount of harmonic vibrations, which do not belong to a Hilbert space
. In the representation of the Fourier integral, the same element in the same space is interpreted by an uncountable amount of harmonic vibrations, which do not belong to a Hilbert space 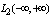 . It is known[3] that what would have been the power of an orthonormal system in a Hilbert space
. It is known[3] that what would have been the power of an orthonormal system in a Hilbert space 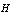 , every vector
, every vector 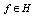 has at most a countable set of nonzero projections on the elements of an orthonormal system. In this regard, seeks to determine the causes of the contradictions in the theory of Fourier integral, as defined in Hilbert space
has at most a countable set of nonzero projections on the elements of an orthonormal system. In this regard, seeks to determine the causes of the contradictions in the theory of Fourier integral, as defined in Hilbert space 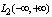 .
.2. Two Models of Representation of Non-Periodic Functions
- Fourier integral is introduced as a generalization of the Fourier series, defined for periodic functions in the event of non-periodic functions[1]. It is known[2] that the function is called a periodic function, if any, the equality
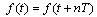 | (1) |
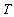 - constant,
- constant, 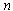 - any integer positive or negative. There are two ideas of generalization of periodic functions represented by Fourier series of harmonic functions with multiple frequencies, the class of aperiodic functions. The first idea of generalization of periodic functions to the class of aperiodic functions is assumed that the infinite increase in the period of the fundamental harmonic
- any integer positive or negative. There are two ideas of generalization of periodic functions represented by Fourier series of harmonic functions with multiple frequencies, the class of aperiodic functions. The first idea of generalization of periodic functions to the class of aperiodic functions is assumed that the infinite increase in the period of the fundamental harmonic 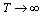 will be obtained non-periodic function[2]. This idea contradicts the definition of a periodic function (1). Known[4] that an infinitely large value is not constant, but variable, and therefore infinitely large value of the period cannot be substituted in formula (1) by definition. If you still do this substitution, we find that for any real value of the argument
will be obtained non-periodic function[2]. This idea contradicts the definition of a periodic function (1). Known[4] that an infinitely large value is not constant, but variable, and therefore infinitely large value of the period cannot be substituted in formula (1) by definition. If you still do this substitution, we find that for any real value of the argument 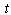 we have
we have 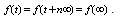 . This equation holds for a variety of functions
. This equation holds for a variety of functions 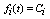 , where
, where 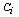 - arbitrary constants,
- arbitrary constants, 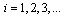 . If
. If 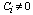 , then such a set of functions does not belong to
, then such a set of functions does not belong to 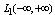 nor to
nor to 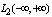 . Only function
. Only function 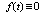 is an element of space
is an element of space 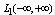 and space
and space 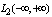 . This leads to the conclusion that the first idea of generalized periodic functions on the class of aperiodic functions will lead to transformation, defined in the space
. This leads to the conclusion that the first idea of generalized periodic functions on the class of aperiodic functions will lead to transformation, defined in the space 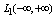 and
and 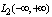 only for one function
only for one function 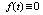 .Another idea is a generalization of periodic functions to the class of non-periodic functions is that the periodic function represented by Fourier series with multiple frequencies, becomes non-periodic function if multiple frequencies replaced by arbitrary incommensurate frequencies. For example, the sum of two harmonic oscillations with finite period, but with differing frequencies, for example,
.Another idea is a generalization of periodic functions to the class of non-periodic functions is that the periodic function represented by Fourier series with multiple frequencies, becomes non-periodic function if multiple frequencies replaced by arbitrary incommensurate frequencies. For example, the sum of two harmonic oscillations with finite period, but with differing frequencies, for example, 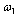 and
and 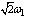 leads to a clearly aperiodic fluctuations[2]. Sum of harmonic vibrations with arbitrary frequencies studied in the theory of almost periodic functions. There are various definitions and generalizations of almost periodic functions. Among them Besicovitch almost periodic functions[5], for which the usual quantity
leads to a clearly aperiodic fluctuations[2]. Sum of harmonic vibrations with arbitrary frequencies studied in the theory of almost periodic functions. There are various definitions and generalizations of almost periodic functions. Among them Besicovitch almost periodic functions[5], for which the usual quantity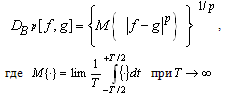 | (2) |
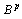 distance. Space of functions summable with a
distance. Space of functions summable with a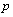 second degree in every finite interval with such a certain distance, called
second degree in every finite interval with such a certain distance, called 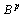 - space.The function
- space.The function 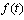 is called almost periodic in Besicovitch
is called almost periodic in Besicovitch 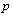 order if there is a sequence of finite trigonometric sums
order if there is a sequence of finite trigonometric sums 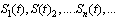 for which
for which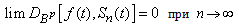 | (3) |
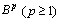 are full. If
are full. If 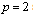 space
space 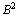 is a Hilbert space in which every almost periodic function
is a Hilbert space in which every almost periodic function 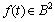 can be associated with a Fourier series
can be associated with a Fourier series 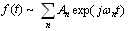 , where
, where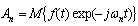 | (4) |
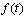 that describe the real dynamic processes that can only have continuous first derivatives
that describe the real dynamic processes that can only have continuous first derivatives 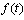 on the whole line. It is known[6] that a function with continuous first derivatives are convergent Fourier series. From the condition (3) that such functions are almost periodic functions in the sense of Besicovitch and belong to the subspace
on the whole line. It is known[6] that a function with continuous first derivatives are convergent Fourier series. From the condition (3) that such functions are almost periodic functions in the sense of Besicovitch and belong to the subspace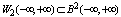 for which the series (4) is uniformly convergent.Thus, there are two Hilbert spaces to describe two models of non-periodic functions. Non-recurrent functions on the first model will be denoted by
for which the series (4) is uniformly convergent.Thus, there are two Hilbert spaces to describe two models of non-periodic functions. Non-recurrent functions on the first model will be denoted by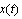 , which presented a Fourier integral in a Hilbert space
, which presented a Fourier integral in a Hilbert space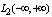 . Nonperiodic functions of the second model, denoted by
. Nonperiodic functions of the second model, denoted by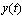 , which seem convergent Fourier series (4) with differing frequencies in a Hilbert space
, which seem convergent Fourier series (4) with differing frequencies in a Hilbert space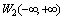 .
.3. The Domain of the Fourier Integral in the Space 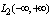
- In the proof of the theorem Plancherel original functional is the functional defining the inner product in Hilbert space
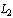 with finite measure[1]. Scalar product
with finite measure[1]. Scalar product 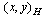 defined in a Hilbert space
defined in a Hilbert space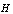 , is only for items
, is only for items 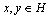 . If the elements
. If the elements 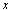 and
and 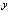 belong to different Hilbert spaces, for example,
belong to different Hilbert spaces, for example, 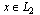 and
and 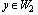 then the inner product
then the inner product 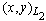 can only be determined on a nonempty subset
can only be determined on a nonempty subset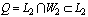 . In this case, the scalar product
. In this case, the scalar product 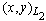 of elements
of elements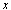 and
and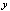 is not defined on the entire space
is not defined on the entire space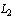 , but only for elements belonging to the subspace
, but only for elements belonging to the subspace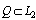 .In the functional Plancherel inner product is for the two functions
.In the functional Plancherel inner product is for the two functions 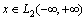 and
and 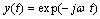 , moreover
, moreover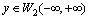 . Let finite functions,
. Let finite functions, 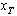 and
and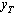 coincide with the functions
coincide with the functions 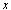 and
and 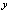 on a finite interval
on a finite interval 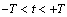 and zero outside this interval. In this case
and zero outside this interval. In this case 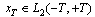 as well
as well 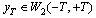 . Define the subspace of finite measure
. Define the subspace of finite measure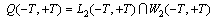 Since nondecreasing integrable
Since nondecreasing integrable 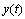 at infinity in finite limits of integration as space
at infinity in finite limits of integration as space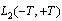 , then
, then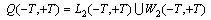 | (5) |
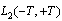 is well-defined inner product for functions of compact support
is well-defined inner product for functions of compact support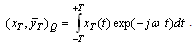 .In the limit
.In the limit  of all functions
of all functions with non-zero norm in the metric
with non-zero norm in the metric 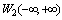 does not belong to a Hilbert space
does not belong to a Hilbert space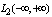 . Therefore
. Therefore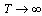 , when condition (5) is not satisfied, but a subset
, when condition (5) is not satisfied, but a subset 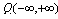 is determined by the suppression of spaces
is determined by the suppression of spaces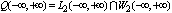 . This subspace contains only one zero element. It follows that the Fourier integral is not defined for all elements
. This subspace contains only one zero element. It follows that the Fourier integral is not defined for all elements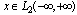 , as stated in the Plancherel theorem, and only one zero element
, as stated in the Plancherel theorem, and only one zero element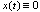 .
.4. Conclusions
- Contradictions that occur when using the Fourier integral for the elements belonging to a Hilbert space
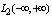 , due to the incorrect assertion that the Fourier integral is applicable to all elements of this space. Fourier transform is defined for a set of functions that form the intersection of the Hilbert space
, due to the incorrect assertion that the Fourier integral is applicable to all elements of this space. Fourier transform is defined for a set of functions that form the intersection of the Hilbert space 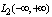 and another Hilbert space with an uncountable harmonic basis
and another Hilbert space with an uncountable harmonic basis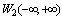 . The intersection of these spaces
. The intersection of these spaces 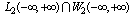 has only one zero element. In the Hilbert space with infinite measure
has only one zero element. In the Hilbert space with infinite measure 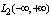 each element of this space with a nonzero norm is a generalized Fourier series in the orthonormal basis, for example, the normalized Hermite functions. Representation of generalized Fourier series is unique, since for functions with non-zero norm of the Fourier integral is not defined. Fourier integral in a Hilbert space
each element of this space with a nonzero norm is a generalized Fourier series in the orthonormal basis, for example, the normalized Hermite functions. Representation of generalized Fourier series is unique, since for functions with non-zero norm of the Fourier integral is not defined. Fourier integral in a Hilbert space 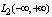 is only defined for the zero element. Dual representation of the zero element side and the Fourier integral is correct, since the zero element at the same time belongs to the Hilbert space of functions decreasing at infinity
is only defined for the zero element. Dual representation of the zero element side and the Fourier integral is correct, since the zero element at the same time belongs to the Hilbert space of functions decreasing at infinity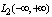 and the Hilbert space with infinite measure of non-decreasing function at infinity
and the Hilbert space with infinite measure of non-decreasing function at infinity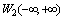 .Functions that describe the real dynamic processes have continuous first derivatives and are represented by convergent Fourier series in harmonic functions. Series with differing frequencies of harmonic components describing aperiodic processes. Nonperiodic processes have discrete spectra. The notion of a continuous spectrum can be introduced formally only in the trivial case when there is a function of the Fourier integral is zero on the entire line.
.Functions that describe the real dynamic processes have continuous first derivatives and are represented by convergent Fourier series in harmonic functions. Series with differing frequencies of harmonic components describing aperiodic processes. Nonperiodic processes have discrete spectra. The notion of a continuous spectrum can be introduced formally only in the trivial case when there is a function of the Fourier integral is zero on the entire line.ACKNOWLEDGEMENTS
- The author expresses his gratitude to A. N. Bondarenko for technical assistance.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML