Twinkle Singh , Mathematics Section
S. V. National Institute of Technology, Surat, Gujarat, 395007, India
Correspondence to: Twinkle Singh , S. V. National Institute of Technology, Surat, Gujarat, 395007, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The basic burger’s equation arising into the fingering phenomena has been converted into perturb burger’s equation by introducing a term such that as and finally it is proved that given solution is not solution of perturb burger’s equation but it is solution of burger’s equation by using appropriate boundary condition under certain standard assumption.
Keywords:
Perturb Burger’s Equation, Fingering Phenomena, Porous Media
Cite this paper:
Twinkle Singh , Mathematics Section , "The Classical Solution of Burger’s Equation Arises into the Fingering Phenomena in Fluid Flow through Homogeneous Porous Media", Applied Mathematics, Vol. 1 No. 2, 2011, pp. 84-86. doi: 10.5923/j.am.20110102.13.
1. Introduction
The present paper discusses the classical solution of burger’s equation which arises into the fingering phenomena in double phase flow through homogenous porous media. When a fluid flowing through a porous media is displaced by another fluid of lesser viscosity then, instead of regular displacement of the whole front, protuberance takes place which shoot through the porous medium at a relatively very high speed. The occurrence of protuberance is called as the instability phenomenon or fingering.For mathematical models it is assumed that there is a uniform water injection into an oil saturated porous medium. The injected water shoots through the oil formation and gives rise to protuberance (fingers). The mathematical formulation yields to non linear partial differential equation in burger’s equation form. For the sack of convinency and theoretical proof we introduce an additional term 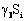 such that as
such that as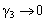 , it does not effect the burger's equation as well as its solution but the basic burger’s equation converts into the perturb burger’s equation Demiray[3]. Finally by the comment by Parkes[1], it has been proved that the solution of perturb burger’s equation given by Demiray[3] is solution of burger’s equation by identification of the error and some over looked the fact by Demiray[3].It is also suggested by Parkes[1] that
, it does not effect the burger's equation as well as its solution but the basic burger’s equation converts into the perturb burger’s equation Demiray[3]. Finally by the comment by Parkes[1], it has been proved that the solution of perturb burger’s equation given by Demiray[3] is solution of burger’s equation by identification of the error and some over looked the fact by Demiray[3].It is also suggested by Parkes[1] that 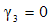 which, as mentioned previously, leads to a solution to the burger’s equation and not, as required, to a solution to the perturb burger’s equation (22).The finally, it is solution of burger’s equation (20) which represent saturation of the i fluid at level, x for any time t0.
which, as mentioned previously, leads to a solution to the burger’s equation and not, as required, to a solution to the perturb burger’s equation (22).The finally, it is solution of burger’s equation (20) which represent saturation of the i fluid at level, x for any time t0.
2. Mathematical Formulation of the Problem and Its Solution
The seepage velocity of water and oil are given by Darcy’s Law as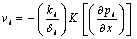 | (1) |
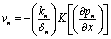 | (2) |
where K is the permeability of the homogeneous medium, k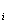 and k
and k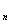 are relative permabilities of water and oil, which are functions of saturations S
are relative permabilities of water and oil, which are functions of saturations S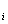 and S
and S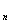 , and
, and 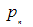 are pressure,
are pressure, 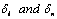 are the constant kinetic viscosity of water and oil respectively.The equation of continuity of two phases densities are regarded as constant, is given as
are the constant kinetic viscosity of water and oil respectively.The equation of continuity of two phases densities are regarded as constant, is given as 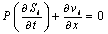 | (3) |
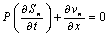 | (4) |
Where P is the porosity of the medium.From the definition of phase saturation, it is evident that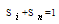 | (5) |
The capillary pressure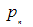 , defined as discontinuity of the flowing phase across their common interface, is a function of the phase saturation. It may be written as
, defined as discontinuity of the flowing phase across their common interface, is a function of the phase saturation. It may be written as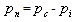 | (6) |
The equation of motion for saturation is obtained by substituting the values of v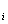 and v
and v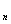 from equations (1) and (2) to the equations (3) and (4) respectively,
from equations (1) and (2) to the equations (3) and (4) respectively,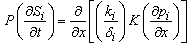 | (7) |
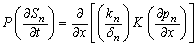 | (8) |
Eliminating 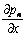 from equation (6) and (7) we have
from equation (6) and (7) we have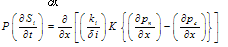 | (9) |
By combining equations (8) and (9), and using equation (5), we get 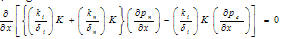 | (10) |
Integrating equation (10) with respect to 'x', we get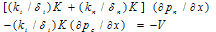 | (11) |
Where V is a constant of integration, which can be evaluated later on. By simplify (11), we get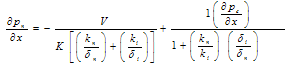 | (12) |
From equation (9,12), the following is obtained 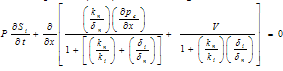 | (13) |
The value of the pressure of oil (p) can be written as 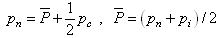 | (14) |
Where 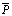 is the constant mean pressure.On differentiating the above equation with respect to x, the following equation is obtained
is the constant mean pressure.On differentiating the above equation with respect to x, the following equation is obtained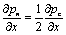 | (15) |
On substuting the value of 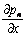 in equation (11) we can obtained,
in equation (11) we can obtained,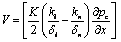 | (16) |
On substuting the value of V from equation (16) and (13), we can obtained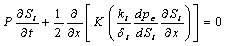 | (17) |
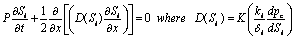 Now, from equation (17) we get
Now, from equation (17) we get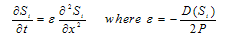 | (18) |
With the help of Hopf-Cole transformation[2,5] 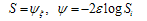 | (19) |
The equation (18) becomes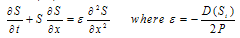 | (20) |
Which s the non-linear burger’s equation arises into the fingering phenomenon in double phase flow through porous media. By rearranging terms of (20), we get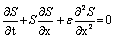 | (21) |
With appropriate Boundary conditionS (0, t) = S0, for t > 0Which is the burger’s equation arises into the fingering phenomenon in double phase flow through porous media.We would like to convert this burger’s equation (21) into perturb burger’s equation by introducing an additional term 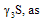
 does not effect the problem as well as solution.Hence equation (21) becomes perturb burger’s equation, Demiray[3].
does not effect the problem as well as solution.Hence equation (21) becomes perturb burger’s equation, Demiray[3].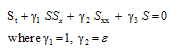 | (22) |
and 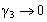 , where
, where 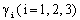 are non-zero constants & it is claimed by Demiray [3] a solution of perturb burger’s equation (22) is
are non-zero constants & it is claimed by Demiray [3] a solution of perturb burger’s equation (22) is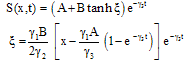 | (23) |
Where A & B are constants. As 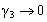 the solution (23) reduces, as required, to the well-known progressive saturation of displacing fluid in porous medium. i.e. the equation to which (22) reduces, where
the solution (23) reduces, as required, to the well-known progressive saturation of displacing fluid in porous medium. i.e. the equation to which (22) reduces, where  .Unfortunately we want to prove that (23) is not solution of (22) as can easily be verified by direct substitution, Parkes[1]. The purpose of this note is to reveal the error in the argument given by Demiray[3]Parkes[1] had identified the error, and by Demiray[3] over looked the fact, made and in this case equation (23) implies that
.Unfortunately we want to prove that (23) is not solution of (22) as can easily be verified by direct substitution, Parkes[1]. The purpose of this note is to reveal the error in the argument given by Demiray[3]Parkes[1] had identified the error, and by Demiray[3] over looked the fact, made and in this case equation (23) implies that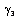 should be zero (i.e.
should be zero (i.e. 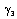 = 0) leads to a solution to the Burger’s equation (21) and not, as required, to a solution to the perturb burger’s equation (22).Hence by Parkes[1] argument it is concluded that equation (23) represents solution of burger’s equation (20) To determine constants A and B, we use Boundary conditions.
= 0) leads to a solution to the Burger’s equation (21) and not, as required, to a solution to the perturb burger’s equation (22).Hence by Parkes[1] argument it is concluded that equation (23) represents solution of burger’s equation (20) To determine constants A and B, we use Boundary conditions.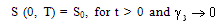 | (24) |
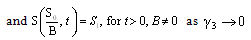 | (25) |
By using condition (24) A = S0.To determine B, we use boundary condition (25) 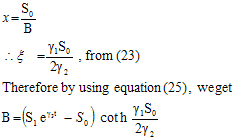
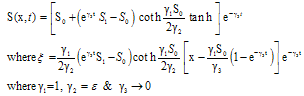 | (26) |
Which represents saturation of displacing fluid in porous media. when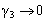 for any distance x for any t > 0.
for any distance x for any t > 0.
3. Conclusions
Here the solution of the fingering phenomenon has obtained given by Demiray[3] is not solution of perturb burger’s equation but it is accepted as solution of burger’s equation (20) with appropriate boundary conditions. The solution satisfies both boundary conditions. For our particular interest graphical as well as numerical solution is also obtained. The solution is in terms of hyperbolic as well as exponential terms.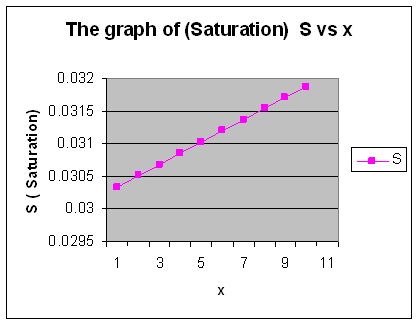 | Figure a. |
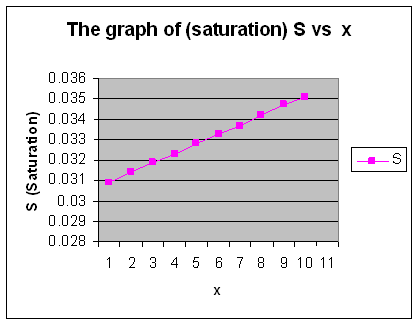 | Figure b. |
| | X | S | X | S | | 1 | 0.03034 | 1 | 0.0309 | | 1.5 | 0.03051 | 1.5 | 0.0314 | | 2 | 0.03068 | 2 | 0.0319 | | 2.5 | 0.03085 | 2.5 | 0.0323 | | 3 | 0.031029 | 3 | 0.0328 | | 3.5 | 0.0312 | 3.5 | 0.0333 | | 4 | 0.03137 | 4 | 0.0337 | | 4.5 | 0.03154 | 4.5 | 0.0342 | | 5 | 0.03171 | 5 | 0.0347 | | 5.5 | 0.03188 | 5.5 | 0.0351 |
|
|
References
| [1] | E. J. Parkes, A note on Demiray’s solution to the perturb Burger’s equation, Applied Mathematical Modeling 27, 487-488, 2003 |
| [2] | E. Hopf. : The partial differential equation ut + uux = uxx comm. Pure Appl. Math. 3, pp – 201-230, 1950 |
| [3] | H. Demiray, A note on the traveling wave solution to the perturbed Burger’s equation, Applied Mathematical modeling pp.26, 37-40. 2002 |
| [4] | J. M. Burgers: A Mathematical model illustrating the theory of turbulence. Adv. Appl. Mech., 4, 5., pp.171-199,1948 |
| [5] | J. D. Cole: On a quasilinear parabolic equation occurring in aerodynamics. Q. Apple. Math. 9, pp. 225-236,1951 |
| [6] | Mehta. M. N.: A Singular perturbation solution of one dimensional flow in unsaturated porous media with small diffusivity coefficient; proc. FMFP, E1 to E4 1975 |
| [7] | Verma.A.P: Stastical behavior of Fingering in a Displacement Process in Heterogeneous Porous medium with Capillary Pressure Canadian Journal of Physics, 47 (3) 319 – 324 1969 |

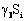 such that as
such that as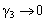 , it does not effect the burger's equation as well as its solution but the basic burger’s equation converts into the perturb burger’s equation Demiray[3]. Finally by the comment by Parkes[1], it has been proved that the solution of perturb burger’s equation given by Demiray[3] is solution of burger’s equation by identification of the error and some over looked the fact by Demiray[3].It is also suggested by Parkes[1] that
, it does not effect the burger's equation as well as its solution but the basic burger’s equation converts into the perturb burger’s equation Demiray[3]. Finally by the comment by Parkes[1], it has been proved that the solution of perturb burger’s equation given by Demiray[3] is solution of burger’s equation by identification of the error and some over looked the fact by Demiray[3].It is also suggested by Parkes[1] that 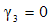 which, as mentioned previously, leads to a solution to the burger’s equation and not, as required, to a solution to the perturb burger’s equation (22).The finally, it is solution of burger’s equation (20) which represent saturation of the i fluid at level, x for any time t0.
which, as mentioned previously, leads to a solution to the burger’s equation and not, as required, to a solution to the perturb burger’s equation (22).The finally, it is solution of burger’s equation (20) which represent saturation of the i fluid at level, x for any time t0.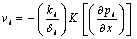
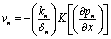
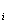 and k
and k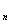 are relative permabilities of water and oil, which are functions of saturations S
are relative permabilities of water and oil, which are functions of saturations S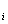 and S
and S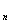 , and
, and 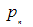 are pressure,
are pressure, 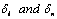 are the constant kinetic viscosity of water and oil respectively.The equation of continuity of two phases densities are regarded as constant, is given as
are the constant kinetic viscosity of water and oil respectively.The equation of continuity of two phases densities are regarded as constant, is given as 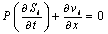
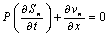
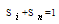
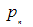 , defined as discontinuity of the flowing phase across their common interface, is a function of the phase saturation. It may be written as
, defined as discontinuity of the flowing phase across their common interface, is a function of the phase saturation. It may be written as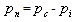
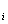 and v
and v from equations (1) and (2) to the equations (3) and (4) respectively,
from equations (1) and (2) to the equations (3) and (4) respectively,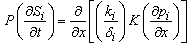
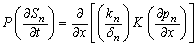
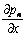 from equation (6) and (7) we have
from equation (6) and (7) we have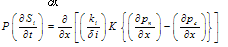
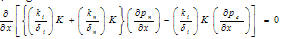
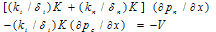
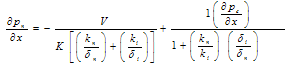
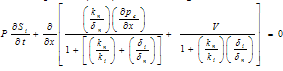
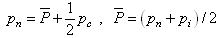
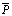 is the constant mean pressure.On differentiating the above equation with respect to x, the following equation is obtained
is the constant mean pressure.On differentiating the above equation with respect to x, the following equation is obtained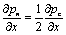
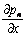 in equation (11) we can obtained,
in equation (11) we can obtained,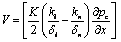
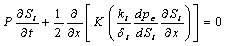
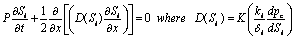 Now, from equation (17) we get
Now, from equation (17) we get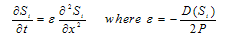
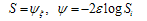
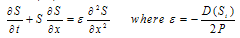
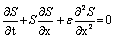
 does not effect the problem as well as solution.Hence equation (21) becomes perturb burger’s equation, Demiray[3].
does not effect the problem as well as solution.Hence equation (21) becomes perturb burger’s equation, Demiray[3].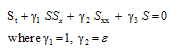
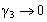 , where
, where 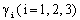 are non-zero constants & it is claimed by Demiray [3] a solution of perturb burger’s equation (22) is
are non-zero constants & it is claimed by Demiray [3] a solution of perturb burger’s equation (22) is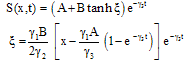
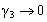 the solution (23) reduces, as required, to the well-known progressive saturation of displacing fluid in porous medium. i.e. the equation to which (22) reduces, where
the solution (23) reduces, as required, to the well-known progressive saturation of displacing fluid in porous medium. i.e. the equation to which (22) reduces, where  .Unfortunately we want to prove that (23) is not solution of (22) as can easily be verified by direct substitution, Parkes[1]. The purpose of this note is to reveal the error in the argument given by Demiray[3]Parkes[1] had identified the error, and by Demiray[3] over looked the fact, made and in this case equation (23) implies that
.Unfortunately we want to prove that (23) is not solution of (22) as can easily be verified by direct substitution, Parkes[1]. The purpose of this note is to reveal the error in the argument given by Demiray[3]Parkes[1] had identified the error, and by Demiray[3] over looked the fact, made and in this case equation (23) implies that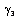 should be zero (i.e.
should be zero (i.e. 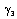 = 0) leads to a solution to the Burger’s equation (21) and not, as required, to a solution to the perturb burger’s equation (22).Hence by Parkes[1] argument it is concluded that equation (23) represents solution of burger’s equation (20) To determine constants A and B, we use Boundary conditions.
= 0) leads to a solution to the Burger’s equation (21) and not, as required, to a solution to the perturb burger’s equation (22).Hence by Parkes[1] argument it is concluded that equation (23) represents solution of burger’s equation (20) To determine constants A and B, we use Boundary conditions.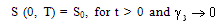
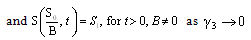
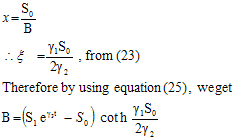
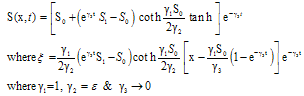
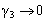 for any distance x for any t > 0.
for any distance x for any t > 0.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML