Habib Jafari, Reza Hashemi
Department of Statistics, Razi University, Kermanshah, Iran
Correspondence to: Habib Jafari, Department of Statistics, Razi University, Kermanshah, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The locally D-optimal design was derived for simple linear regression with the error term of Skew-Normal distribution. In this paper, to obtain a D-optimal design, the locally D-optimal criterion was considered, because of depending the information matrix on unknown parameters.
Keywords:
Information Matrix, Skew-Normal Distribution, Locally D-Optimal Criterion, Locally A-Optimal Criterion, Locally D- And A-Optimal Design
Cite this paper: Habib Jafari, Reza Hashemi, Optimal Designs in a Simple Linear Regression with Skew-Normal Distribution for Error Term, Applied Mathematics, Vol. 1 No. 2, 2011, pp. 65-68. doi: 10.5923/j.am.20110102.11.
1. Introduction
There are many papers which discuss the optimal design for simple linear regression when the error terms have normal distribution. In this paper, the Skew-Normal distribution was considered for error term. The central role of general random variables in probability and statistics is well-known and can be traced to the simplicity of the functional forms, basic symmetry properties of the probability density function (pdf) and cumulative function (cdf) of the standard normal random variable, Z;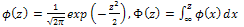 | (1) |
Now, the following function can be considered: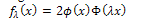 | (2) |
is a bona fide pdf of a random variable X which inherits a few features of the normal random variables. Some of these features happen to be the ones which make the normal distribution the darling of statistical inference.The class of distribution (2) was introduced in[2] and Christened Skew-Normal distribution with the skewness parameter , in symbol X
, in symbol X SN (
SN (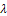 ). The right-tails of these distributions are virtually indistinguishable for
). The right-tails of these distributions are virtually indistinguishable for 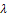 > 2; thus, in this paper, only optimal design was discussed for
> 2; thus, in this paper, only optimal design was discussed for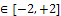 . Some properties of this kind of distribution can be found in[7].In this paper, a simple linear regression model was considered as well as
. Some properties of this kind of distribution can be found in[7].In this paper, a simple linear regression model was considered as well as 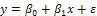 , where the error term had skew-normal distribution with- parameter
, where the error term had skew-normal distribution with- parameter 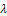 ; meaning that,
; meaning that, 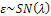 . In this situation, Y has also skew-normal distribution with the following pdf;
. In this situation, Y has also skew-normal distribution with the following pdf;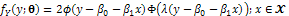 | (3) |
where 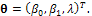 As was already written, is obtaining of this paper was to obtain the locally D-optimal design of this model based on the unknown parameter vector θ.In this paper, there was concentration on the criterion dependence on the variance of parameter estimator. As is known, the variance of parameter estimator (ML) is inversely proportional to the information matrix[2]. Thus, there have been searched designs maximizing the information on the estimates as represented in the Fisher information matrix in
As was already written, is obtaining of this paper was to obtain the locally D-optimal design of this model based on the unknown parameter vector θ.In this paper, there was concentration on the criterion dependence on the variance of parameter estimator. As is known, the variance of parameter estimator (ML) is inversely proportional to the information matrix[2]. Thus, there have been searched designs maximizing the information on the estimates as represented in the Fisher information matrix in 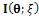 , where
, where 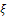 denotes a design. The outline of the paper is as follows. In Section 2, the information matrix, the locally D-optimal criterion which is a function of the information matrix and the locally D-optimal design for model (3) are introduced. At last, conclusion is made in Section 3.
denotes a design. The outline of the paper is as follows. In Section 2, the information matrix, the locally D-optimal criterion which is a function of the information matrix and the locally D-optimal design for model (3) are introduced. At last, conclusion is made in Section 3.
2. Locally D-optimal Design
To obtain the D-optimal deign, the information matrix should be known, which was calculated using the derivative degree two of the log-likelihood function. In this paper, the information matrix was obtained based on the following log-likelihood function according to model (3);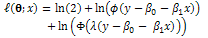 | (4) |
At first, since the information matrix should be calculated for one observation, (for one observation) was obtained by;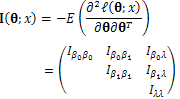 | (5) |
where the elements of the symmetry information matrix (5) were as follows;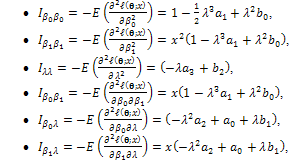 such that;
such that;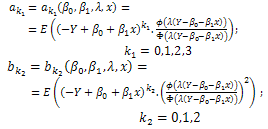 See Appendix A1.Especially, suppose
See Appendix A1.Especially, suppose 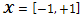 as design space and
as design space and 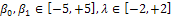 . Now, for all the values of
. Now, for all the values of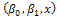 , the following can be written; • Two amounts of
, the following can be written; • Two amounts of 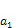 and
and 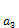 are equal to zero and
are equal to zero and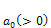 increase for
increase for 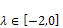 and decrease for
and decrease for 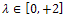 . There exists a similar position for
. There exists a similar position for 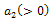 , where;
, where;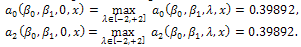 •
• 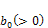 increases for
increases for 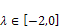 and decreases for
and decreases for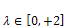 . There exists a similar position for
. There exists a similar position for 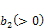 , where;
, where; 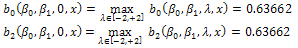 In this case,
In this case, 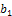 increases as
increases as 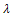 increases and
increases and 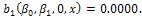 After proposing the two above properties (items 1 and 2), an optimal design should be obtained for model (3). As is known, there are many optimality criteria for obtaining an optimal design such that D- and A-optimality criteria which are functions of the information matrix (5) and shown by the following notations[1];
After proposing the two above properties (items 1 and 2), an optimal design should be obtained for model (3). As is known, there are many optimality criteria for obtaining an optimal design such that D- and A-optimality criteria which are functions of the information matrix (5) and shown by the following notations[1];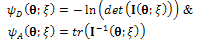 | (7) |
where 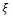 denotes a design with two components; the first components are some values of design space
denotes a design with two components; the first components are some values of design space 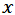 and the weight of them are the second components, so that design
and the weight of them are the second components, so that design 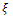 can be defined as follows;
can be defined as follows;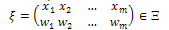 | (8) |
where 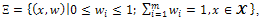 ,
, 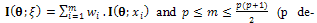 (p denotes the number of parameters)[5]. The design is called the saturated design when m=p.In Table 1, an optimal design is shown for model (3) based on the information matrix (5). In this case, for different amounts of parameter
(p denotes the number of parameters)[5]. The design is called the saturated design when m=p.In Table 1, an optimal design is shown for model (3) based on the information matrix (5). In this case, for different amounts of parameter 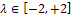 and every value of
and every value of 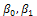 in the interval [-5, +5] and also the equivalence Theorem[6] (See Appendix A2), the following can be written[9];
in the interval [-5, +5] and also the equivalence Theorem[6] (See Appendix A2), the following can be written[9];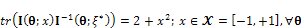 | (10) |
Table 1. Locally D- and A-optimal design for some values of λ and any values of the other parameters
 |
| |
|
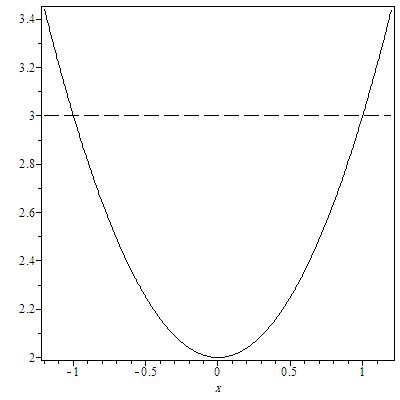 | Figure 1. 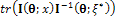 |
According to Equation (10), Figure 1 shows that in the two points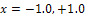 ,
, 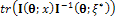 is equal to 3; but, for
is equal to 3; but, for 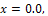 this quantity is less than 3 (the number of parameters). Then, it can be said that the following locally D-optimal design exists with two support points -1, +1;
this quantity is less than 3 (the number of parameters). Then, it can be said that the following locally D-optimal design exists with two support points -1, +1; In this case, it can be also seen that the maximum of the determinant of the information matrix exists when
In this case, it can be also seen that the maximum of the determinant of the information matrix exists when 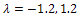 in Table 1.
in Table 1.
3. Conclusions
In this paper, the Skew-normal distribution was considered for error term in simple linear regression. In this kind of model, there are three parameters, two of which are related to the regression model and one is the parameter of Skew-normal distribution. Then, based on these three parameters and Caratheodory’s theorem[3], a design with three support points assumed. To obtain an optimal design, the D-optimal criterion was considered. In this case, due to the dependence of the information matrix on unknown parameters, the locally D-optimal design was obtained[8].In this situation, there was only one locally D-optimal design for every value of the parameters 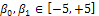 and for different values of
and for different values of 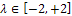 . This result is shown in Table 1, where
. This result is shown in Table 1, where 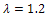 maximizes the determinate of the information matrix. Also, it was shown that locally A-optimal design was the same as locally D-optimal design, where
maximizes the determinate of the information matrix. Also, it was shown that locally A-optimal design was the same as locally D-optimal design, where 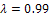 minimizes
minimizes 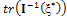 (Table 1).
(Table 1).
Appendix A1:
To calculate the elements of the information matrix (5), the derivatives of the log-likelihood function (4) with respect to three parameters 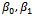 and λ is needed as follows;
and λ is needed as follows;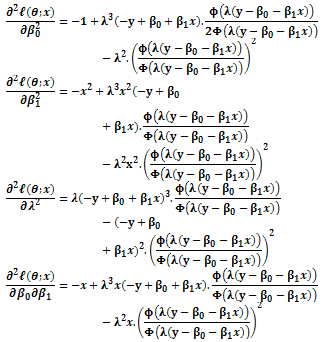
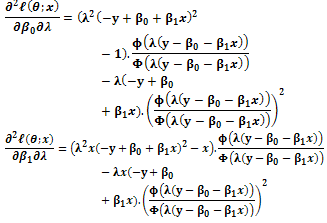
Appendix A2:
Theorem (Equivalence Theorem)[9]: Based on the design 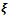 the following three items are equivalent:•
the following three items are equivalent:• 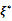 is the locally D-optimal design if:
is the locally D-optimal design if: 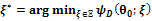 , where
, where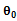 denotes the true value of parameters.•
denotes the true value of parameters.• 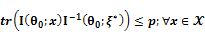 (G-optimality criterion), p denotes the number of parameters.•
(G-optimality criterion), p denotes the number of parameters.• 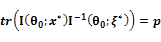 , where
, where 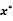 is the support points.
is the support points.
References
| [1] | A. Atkinson, A. Donev and R. Tobias. (2007), Optimum experimental designs with SAS, Oxford Uni. Press |
| [2] | A. Azzalini. (1985). A class of distribution which includes the normal ones, Scand. J. Stat., 12, 171-178 |
| [3] | V. V. Fedorov. (1972). Theory of optimal experiments. Academic Press, New York |
| [4] | W. Hector and S. Hugo. (2010). Information matrix for generalized Skew-normal distribution. Proyecciones Journal of Mathematics, 29, 2, pp. 83-92 |
| [5] | J. Kiefer and J. Wolfowitz (1959). Optimum designs in regression problems (I). Annals of Mathematical Statistics, Vol.30, No.2, 271-294 |
| [6] | J. Kiefer and J. Wolfowitz (1960). The equivalence of two extremum problems. Canadian Journal of Mathematics, Vol. 12, 363-366 |
| [7] | M. Pourahmadi (preprint). Construction of Skew-Normal random variables: Are they linear combination of normal half-normal? |
| [8] | C. Stefano, R. Walter and V. Laura (Preprint). Bayesian inference on the scalar Skew- normal distribution |
| [9] | L. V. White (1973). An extension of general equivalence theorem to nonlinear models. Biometrika, Vol. 60, No.2, 345-348 |

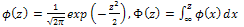
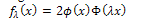
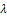 , in symbol X
, in symbol X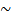 SN (
SN (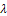 ). The right-tails of these distributions are virtually indistinguishable for
). The right-tails of these distributions are virtually indistinguishable for 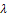 > 2; thus, in this paper, only optimal design was discussed for
> 2; thus, in this paper, only optimal design was discussed for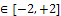 . Some properties of this kind of distribution can be found in[7].In this paper, a simple linear regression model was considered as well as
. Some properties of this kind of distribution can be found in[7].In this paper, a simple linear regression model was considered as well as 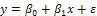 , where the error term had skew-normal distribution with- parameter
, where the error term had skew-normal distribution with- parameter 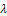 ; meaning that,
; meaning that, 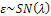 . In this situation, Y has also skew-normal distribution with the following pdf;
. In this situation, Y has also skew-normal distribution with the following pdf;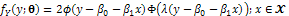
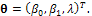 As was already written, is obtaining of this paper was to obtain the locally D-optimal design of this model based on the unknown parameter vector θ.In this paper, there was concentration on the criterion dependence on the variance of parameter estimator. As is known, the variance of parameter estimator (ML) is inversely proportional to the information matrix[2]. Thus, there have been searched designs maximizing the information on the estimates as represented in the Fisher information matrix in
As was already written, is obtaining of this paper was to obtain the locally D-optimal design of this model based on the unknown parameter vector θ.In this paper, there was concentration on the criterion dependence on the variance of parameter estimator. As is known, the variance of parameter estimator (ML) is inversely proportional to the information matrix[2]. Thus, there have been searched designs maximizing the information on the estimates as represented in the Fisher information matrix in 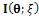 , where
, where 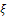 denotes a design. The outline of the paper is as follows. In Section 2, the information matrix, the locally D-optimal criterion which is a function of the information matrix and the locally D-optimal design for model (3) are introduced. At last, conclusion is made in Section 3.
denotes a design. The outline of the paper is as follows. In Section 2, the information matrix, the locally D-optimal criterion which is a function of the information matrix and the locally D-optimal design for model (3) are introduced. At last, conclusion is made in Section 3.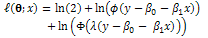
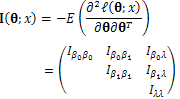
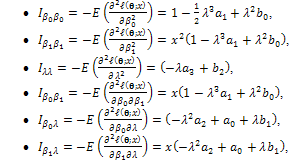 such that;
such that;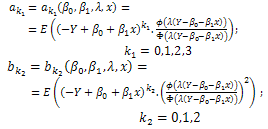 See Appendix A1.Especially, suppose
See Appendix A1.Especially, suppose  as design space and
as design space and  . Now, for all the values of
. Now, for all the values of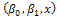 , the following can be written; • Two amounts of
, the following can be written; • Two amounts of 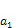 and
and 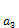 are equal to zero and
are equal to zero and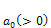 increase for
increase for 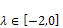 and decrease for
and decrease for 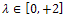 . There exists a similar position for
. There exists a similar position for 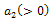 , where;
, where;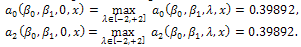 •
• 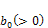 increases for
increases for 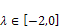 and decreases for
and decreases for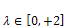 . There exists a similar position for
. There exists a similar position for 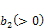 , where;
, where; 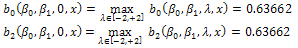 In this case,
In this case, 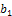 increases as
increases as 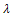 increases and
increases and 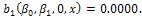 After proposing the two above properties (items 1 and 2), an optimal design should be obtained for model (3). As is known, there are many optimality criteria for obtaining an optimal design such that D- and A-optimality criteria which are functions of the information matrix (5) and shown by the following notations[1];
After proposing the two above properties (items 1 and 2), an optimal design should be obtained for model (3). As is known, there are many optimality criteria for obtaining an optimal design such that D- and A-optimality criteria which are functions of the information matrix (5) and shown by the following notations[1];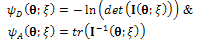
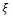 denotes a design with two components; the first components are some values of design space
denotes a design with two components; the first components are some values of design space 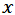 and the weight of them are the second components, so that design
and the weight of them are the second components, so that design 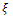 can be defined as follows;
can be defined as follows;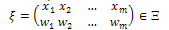
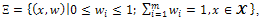 ,
, 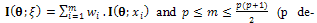 (p denotes the number of parameters)[5]. The design is called the saturated design when m=p.In Table 1, an optimal design is shown for model (3) based on the information matrix (5). In this case, for different amounts of parameter
(p denotes the number of parameters)[5]. The design is called the saturated design when m=p.In Table 1, an optimal design is shown for model (3) based on the information matrix (5). In this case, for different amounts of parameter 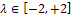 and every value of
and every value of 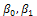 in the interval [-5, +5] and also the equivalence Theorem[6] (See Appendix A2), the following can be written[9];
in the interval [-5, +5] and also the equivalence Theorem[6] (See Appendix A2), the following can be written[9];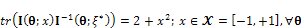

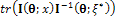
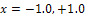 ,
, 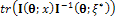 is equal to 3; but, for
is equal to 3; but, for 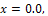 this quantity is less than 3 (the number of parameters). Then, it can be said that the following locally D-optimal design exists with two support points -1, +1;
this quantity is less than 3 (the number of parameters). Then, it can be said that the following locally D-optimal design exists with two support points -1, +1; In this case, it can be also seen that the maximum of the determinant of the information matrix exists when
In this case, it can be also seen that the maximum of the determinant of the information matrix exists when 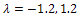 in Table 1.
in Table 1. and for different values of
and for different values of 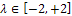 . This result is shown in Table 1, where
. This result is shown in Table 1, where 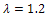 maximizes the determinate of the information matrix. Also, it was shown that locally A-optimal design was the same as locally D-optimal design, where
maximizes the determinate of the information matrix. Also, it was shown that locally A-optimal design was the same as locally D-optimal design, where 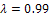 minimizes
minimizes 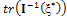 (Table 1).
(Table 1).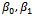 and λ is needed as follows;
and λ is needed as follows;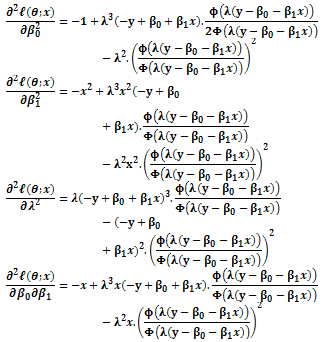
 the following three items are equivalent:•
the following three items are equivalent:• 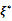 is the locally D-optimal design if:
is the locally D-optimal design if: 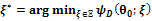 , where
, where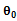 denotes the true value of parameters.•
denotes the true value of parameters.• 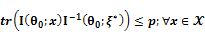 (G-optimality criterion), p denotes the number of parameters.•
(G-optimality criterion), p denotes the number of parameters.• 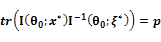 , where
, where 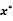 is the support points.
is the support points. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML