Rakesh Kumar
School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post-Office, University Campus, Jammu and Kashmir, Post-Code 182320, India
Correspondence to: Rakesh Kumar , School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post-Office, University Campus, Jammu and Kashmir, Post-Code 182320, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Non- Markovian queuing models have their place in modeling the real life phenomena. In fact, their utility get enhanced when one is not able to get a particular probability distribution for either the inter-arrival times or for the service times. The service times are assumed to have general service time distribution in case of computer communication modeling. Recently, the emphasis is put on the catastrophe modeling and its applications in real situations. Keeping this in view, an M/G/1 queuing model has been developed with catastrophic and restorative effects. The steady-state solution of the model has been obtained using supplementary variable technique. Some queuing models have been obtained as particular cases of this model.
Keywords:
Queuing System, Restoration Times, Catastrophic Effect, Steady-State Solution
Cite this paper:
Rakesh Kumar , "Steady State Solution of a Catastrophic-cum-Restorative M/G/1 Queuing System Using Supplementary Variable Technique", Applied Mathematics, Vol. 1 No. 2, 2011, pp. 62-64. doi: 10.5923/j.am.20110102.10.
1. Introduction
Catastrophe modeling and analysis has been playing a vital role in various areas of science and technology. The notion of catastrophes occurring at random, leading to the annihilation of all the customers there and momentarily inactivation of service facility until a new arrival of a customer, is not uncommon in many practical problems. Chao has modeled computer networks with a virus by queuing networks with catastrophes[1]. Jain and Kumar[2] introduced the concept of restoration in catastrophic queues. According to them, any system suffering from catastrophe will always require some sort of time to function in a normal way, which is taken as restoration time. During the process of restoration, no arrival is allowed to join the system. Kumar[3-5] studied some queuing models with catastrophic and restorative effects. Jain and Kumar[6] studied M/G/1 queue in presence of catastrophes. Di Crescenzo et al[7] studied a double ended queuing model with catastrophes and repair and obtained the transient and steady-state solutions. Tarabia[8] performed the transient and steady-state analysis of an M/M/1queue with balking, catastrophes, server failures and repairs using the generating function and direct approach. Park et al[9] studied the GI/Geo/1 queue with catastrophes and obtained the steady state solution. Thangaraj and Vani-tha[10] studied an M/M/1queue with catastrophes and obtained the transient solution using continued fractions. Bohm[11] discussed various queuing systems with total disasters.This paper is the generalization of the paper studied by Jain and Kumar[6] in the sense that the idea of restoration has been incorporated in the M/G/1 queue with catastrophes. This type of queuing system finds its application in computer communication networks where an arrival of a virus may cause catastrophe (i.e. annihilates all the packets in the buffer) and the recovery/scanning time of viruses may be modeled as restoration time. The steady-state solution of the model has been obtained using Supplementary Variable technique. The rest of the paper has been arranged as follows: in section 2, the queuing model has been formulated; section 3 deals with the steady-state solution of the model and the model has been concluded in section 4.
2. Formulation of Queuing Model
The queuing model under consideration is based on the following assumptions:(i) The arrivals occur in a Poisson stream with mean rateλ.(ii) The service time distribution is general with cumulative distribution function (CDF) B(x) and density function b(x), which has mean β. (iii) The queue discipline is FCFS.(iv) When the system is not empty the catastrophes may occur at the service facility according to a Poisson process with rate ξ. The catastrophes annihilate all the customers in the system instantaneously and the system starts working after the restoration process is over. The arrivals are not allowed during restoration periods.(v) The restoration times are independently, identically and exponentially distributed with parameter γ.
3. Steady-state Solution of the Queuing Model
Supplementary variable technique has been employed to derive the steady-state solution of the model.Define, Pn (x, t) dx = the joint probability that at time t there are n units waiting in the queue and the elapsed service time of the unit in service lies in the interval (x, x + dx ); n ≥0.P00 (t) = the probability that at time t the system is empty without the occurrence of catastrophe. Q00 (t) = the probability that at time t the system is empty with the occurrence of catastrophe. In steady state,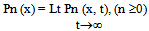 | (1) |
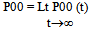 | (2) |
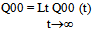 | (3) |
Let η(x) be the conditional probability density of a service completion given that elapsed service time is x, so that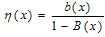 | (4) |
From (3), on integration, we have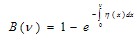 | (5) |
and therefore, 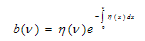 | (6) |
The steady state equations governing the model are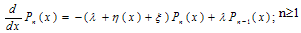 | (7) |
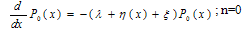 | (8) |
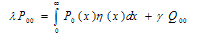 | (9) |
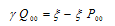 | (10) |
These equations are to be solved with the following boundary conditions: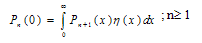 | (11) |
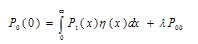 | (12) |
and the normalizing condition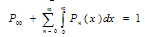 | (13) |
The probability P n of finding n customers in the queue, irrespective of the value of x is given by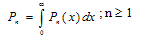 | (14) |
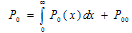 | (15) |
Define the generating functions by 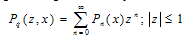 | (16) |
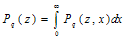 | (17) |
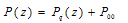 | (18) |
Multiply (7) by zn summing over the range of n and adding (8), we have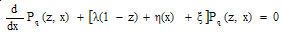 | (19) |
Whose solution is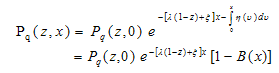 | (20) |
Hence,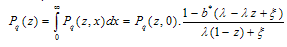 | (21) |
Where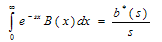 | (22) |
In order to evaluate, multiplying (11) and (12) by appropriate powers of z and adding, we have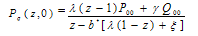 | (23) |
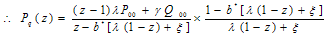 | (24) |
Hence,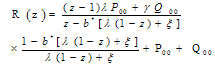 | (25) |
Now, Q00 can be evaluated from equation (10) as 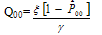 | (26) |
Also P00 can be can be obtained by using the normalizing condition as 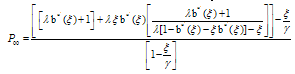 | (27) |
Thus, the steady-state solution of the M/G/1 queue with catastrophic and restorative effects has been obtained.
3.1. Particular Cases
(i) When γ = ∞ (no restoration occurs)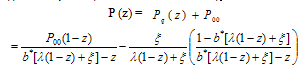 | (28) |
Where 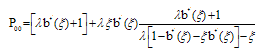 | (29) |
and Q00 = 0(28) and (29) provide the probability generating function of system size of an M/G/1 queue with catastrophes which is studied by Jain and Kumar[6].(ii) When ζ=0 and γ = ∞ (no catastrophes and no restoration)The equations (23) and (24) giveWhich is the steady state probability generating function of simple M/G/1 queue.
4. Conclusions
This paper discusses an M/G/1 queuing system with catastrophic and restorative effects. The steady-state solution of the model has been derived. This model finds its application in computer-communication.
References
| [1] | Chao, X.,1995, A queuing network model with catastrophes and product form Solution, Operations Research Letters, 18, 75-79 |
| [2] | Jain, N. K. and Kumar, R., 2007, Transient Solution of a catastrophic-cum- restorative queuing problem with correlated arrivals and variable service capacity, International Journal of Information and Management Sciences, 18 (4) 461-465 |
| [3] | Kumar, R., 2008, A catastrophic-cum-restorative queuing system with correlated batch arrivals and variable capacity, Pakistan Journal of Statistics and Operations Research, 4(2), 55-62 |
| [4] | Kumar, R., 2009, A catastrophic-cum-restorative queuing model with correlated input for the cell traffic generated by new broadband services, African Journal of Mathematics and Computer Science Research, 2(10), 225-229 |
| [5] | Kumar, R., 2010, Transient solution of a cata Strophic - cum- restorative M/M//2 queue with heterogeneous servers, Pakistan Journal of Statistics, 26 (4) 609-613 |
| [6] | Jain, N. K. and Kumar, R., 2005, M/G/1 Queue with Catastrophes, Indian Journal of Mathematics and Mathematical Sciences,1(1), 45-50 |
| [7] | Di Crescenzo, A., Virginia G., Kumar, B. K., and Nobile, A. G., 2011, A double-ended queue with catastrophes and repairs,and a jump-diffusion approximation, Methodology and Computing in Applied Probability, e-print-arXiv/1101.5073, doi= 10.1007/s11009-011-9214-2 |
| [8] | Tarabia, A.M.K., 2011, Transient and steady-state analysis of an M/M/1queue with balking, catastrophes, server failures and repairs, Journal of Industrial and management optimization, 7(4), 811-823 |
| [9] | Park, H. M., Yang, W. S. and Chae, K. C., 2009, Analysis of GI/Geo/1 queue with disasters, Stochastic analysis and applications, 28(1), 44-53 |
| [10] | Thangaraj, V., and Vanitha, S., 2009, On the analysis of M/M/1feedback queue with catastrophes using continued fractions, International Journal of Pure and Applied Mathematics, 53(1), 133-151 |
| [11] | Bohm, W., 2008, A note on queuing systems exposed to disasters, http://statmath.wu-wien.ac.at/ |

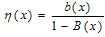
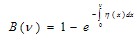
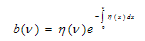
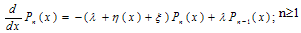
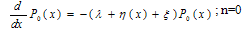
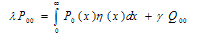
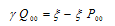
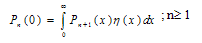
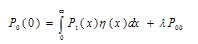
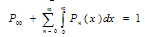
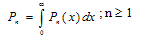
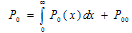
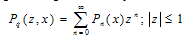
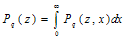
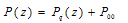
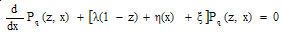
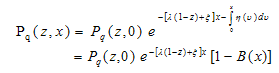
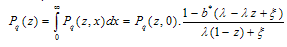
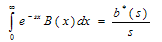
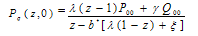
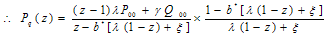
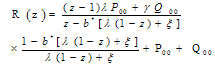
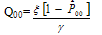
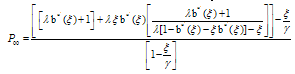
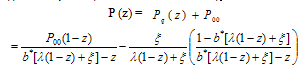
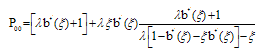
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML