| [1] | A. A. Soliman, 2006, The modified extended tanh-function method for solving Burgers type equations, Physica A,, 361(2), 394-404 |
| [2] | A. H. A. Ali, A. A. Soliman and K. R. Raslan, 2007, Soliton Solution for nonlinear partial differential equations by Cosine-function method, Physics Letters A, 368, 299-304 |
| [3] | B. Wang and W. Yang, 1997, Finite-dimensional behaviour for the Benjamin-Bona-Mahony equation, J. Phys. A: Math. Gen., 30, 4877–4885 |
| [4] | B. Wang, 1998, Regularity of attractors for the Benjamin-Bona-Mahony equation, J. Phys. A: Math. Gen., 31, 7635–7645 |
| [5] | C. T. Yan, 1996, A simple transformation for nonlinear waves, Phys. Lett. A., 224, 77-84 |
| [6] | C. Bai, X. Liu and H. Zhao, 2005, New localized excitations in a (2+1)-dimensional Broer-Kaup system, Chin. Phys., 14(2), 0285–0292 |
| [7] | D. Kaup, 1975, A higher-order water-wave equation and the method for solving it, Prog. Theor. Phys., 54, 396–408 |
| [8] | E. J. Parker and B. R. Duffy, 1996, An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equations, Comput. Phys. Commun., 98, 288-300 |
| [9] | E. Fan, 2001, Soliton solutions for a generalized Hirota-Satsuma coupled KdV equation and a coupled MKdV equation. Phys. Lett. A., 282, 18-22 |
| [10] | E. Fan and H. Zhang, 2003, A new algebraic method for finding the line solitons and doubly periodic wave solution to a two-dimensional perturbed kdv equation, Chaos, Solitons and Fractals, 15, 567–574 |
| [11] | H. Zhang, G. M. Wei and Y. T. Gao, 2001, On the general form of the BenjaminBona-Mahony equation in fluid mechanics, Czechoslovak Journal of Physics, 51, 373–377 |
| [12] | J. S. Russel, Report on waves, Rep. 14th Meet. Brit. Assoc. Adv. Sci., John Murray, York, London, 1844, 311-390 |
| [13] | K. Dogan, 2004, An application of the decomposition method for the KdVB equation, Applied Mathematics and Computation, 152(1), 279–288 |
| [14] | R. Conte and M. Musette, 1992, Link between solitary waves and projective Riccati equations, Phys. A: Math. Gen., 25(21), 5609–5623 |
| [15] | S. A. El-Wakil, S. K. El-Labany, M.A. Zahran and R. Sabry, 2002, Modified extended tanh-function method for solving nonlinear partial differential equations, Phys. Lett. A., 299, 179-188 |
| [16] | S. Zhang, B. Wu and S. Lou, 2002, Painleve analysis and special solutions of generalized Broer-Kaup equations, Phys Lett. A., 300, 40–48 |
| [17] | W. Hong and Y. Jung, 1999, Auto-backlund transformation and analytic solutions for general variable-coefficient KdV equation. Phys Lett. A., 257(3), 149–152 |
| [18] | Y. Zhang and D. Chen, 2004, Backlund transformation and soliton solutions for the shallow water wave equation. Chaos Solitons and Fractals, 20(2), 343–351 |
| [19] | Z. Wang et al., 2005, A method for constructing exact solutions and application to Benjamin Ono equation, Chin. Phys., 14(11), 2158–2163 |
| [20] | Abdul Majid Wazwaz, 2009, Partial Differential Equations and Solitary Waves Theory, Springer-Verlag, Heidelberg |
| [21] | G. W. Bluman and S. Kumei, 1989, Symmetries and Differential Equations. Springer-Verlag, Berlin |
| [22] | P. J. Olver, 1993, Applications of Lie Groups to Differential Equations, Springer-Verlag, New York |
| [23] | V. B. Matveev and M. A. Salle, 1991, Darboux Transformation and Solitons, Springer-Verlag, Berlin |

 tends to infinity, and that solitary waves that move with different speeds, undergo a nonlinear interaction from which they emerge in their original shape.The Benjamin–Bona–Mahony (BBM) equation has been investigated as a regularized version of the Korteweg–de Vries equation for shallow water waves[11]. It incorporates nonlinear dispersive and dissipative effects[3,4]. In certain theoretical investigations the equation is superior as a model for long waves, and the word “regularized” refers to the fact that, from the standpoint of existence and stability, the equation offers considerable technical advantages over the Korteweg–de Vries equation. In addition to shallow water waves, the equation is applicable to the study of drift waves in plasma or the Rossby waves in rotating fluids. Under certain conditions, it also provides a model of one-dimensional transmitted waves. These find applications in semiconductor devices, optical devices, etc[11]. Apart from these applications, solutions to the BBM equation are interesting in and of themselves.The aim of this paper is to apply the cosine function-method to obtain the exact solutions for the two different types of nonlinear partial differential equations such as, Benjamin-Bona-Mahony (BBM) equation and Modified Regularized Long Wave (MRLW) equation which are the important soliton equations.
tends to infinity, and that solitary waves that move with different speeds, undergo a nonlinear interaction from which they emerge in their original shape.The Benjamin–Bona–Mahony (BBM) equation has been investigated as a regularized version of the Korteweg–de Vries equation for shallow water waves[11]. It incorporates nonlinear dispersive and dissipative effects[3,4]. In certain theoretical investigations the equation is superior as a model for long waves, and the word “regularized” refers to the fact that, from the standpoint of existence and stability, the equation offers considerable technical advantages over the Korteweg–de Vries equation. In addition to shallow water waves, the equation is applicable to the study of drift waves in plasma or the Rossby waves in rotating fluids. Under certain conditions, it also provides a model of one-dimensional transmitted waves. These find applications in semiconductor devices, optical devices, etc[11]. Apart from these applications, solutions to the BBM equation are interesting in and of themselves.The aim of this paper is to apply the cosine function-method to obtain the exact solutions for the two different types of nonlinear partial differential equations such as, Benjamin-Bona-Mahony (BBM) equation and Modified Regularized Long Wave (MRLW) equation which are the important soliton equations.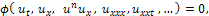
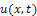 is the solution of (1);
is the solution of (1); 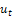 and
and 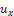 etc. are the partial derivatives of
etc. are the partial derivatives of 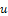 with respect to t and x, respectively. We assume that equation (1) admits travelling wave solution. We use the transformation
with respect to t and x, respectively. We assume that equation (1) admits travelling wave solution. We use the transformation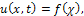 where
where 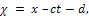 c is the speed of the travelling wave and
c is the speed of the travelling wave and 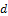 is a constant. This enables us to use the following changes:
is a constant. This enables us to use the following changes: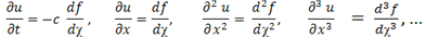
 we obtain
we obtain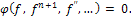
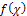 in the following form
in the following form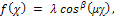
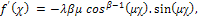 and the second derivative of (5) yields
and the second derivative of (5) yields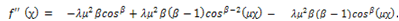
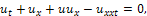
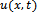 is the solution of (7),
is the solution of (7), 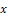 is the space variable and
is the space variable and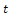 is the time.Using the above procedure we obtain
is the time.Using the above procedure we obtain 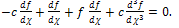
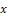 , we obtain
, we obtain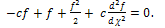
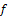 and
and 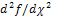 from (5) and (6) in (9) we obtain
from (5) and (6) in (9) we obtain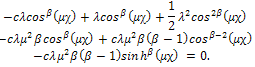
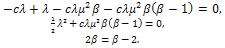
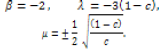 Thus, the exact soliton solution of the BBM equation is
Thus, the exact soliton solution of the BBM equation is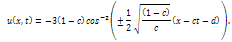
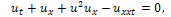
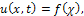 is the solution of (12),
is the solution of (12), 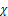 is the space variable and
is the space variable and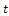 is the time.Using the above procedure we obtain:
is the time.Using the above procedure we obtain: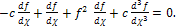
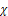 we obtain
we obtain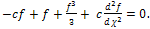
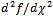 from (5) and (6) in (14) we obtain
from (5) and (6) in (14) we obtain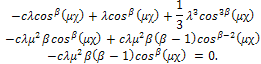

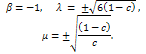 Thus, the exact soliton solution of the MRLW equation is
Thus, the exact soliton solution of the MRLW equation is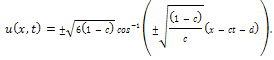
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML