-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(1): 50-55
doi: 10.5923/j.am.20110101.07
Modelling Coagulation Systems: A Stochastic Approach
Vasiliy Ryazanov
Institute for Nuclear Research, Pr. Nauki, 47, 03068, Kiev, Ukraine
Correspondence to: Vasiliy Ryazanov , Institute for Nuclear Research, Pr. Nauki, 47, 03068, Kiev, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A general stochastic approach to the description of coagulating aerosol system is developed. As the object of description one can consider arbitrary mesoscopic values (number of aerosol clusters, their size etc). The birth-and-death formalism for a number of clusters can be regarded as a partial case of the generalized storage model. An application of the storage model to the number of monomers in a cluster is discussed.
Keywords: Stochastic Models, Storage Model, Mesoscopic Description, Kinetic Equation
Cite this paper: Vasiliy Ryazanov , "Modelling Coagulation Systems: A Stochastic Approach", Applied Mathematics, Vol. 1 No. 1, 2011, pp. 50-55. doi: 10.5923/j.am.20110101.07.
Article Outline
1. Introduction
- The stochastic description of the coagulation process was performed in papers like (Scott,1977; Bayewitz et all, 1971; Lushnikov, 1978; Merculovich, Stepanov, 1985, 1986, 1991). So, the birth-and-death model leads to the kinetic equation of coagulation in the form
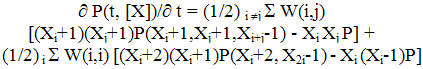 | (1) |
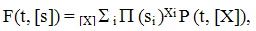 | (2) |
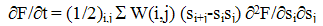 | (3) |
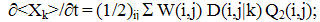 | (4) |
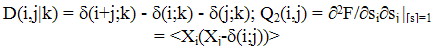 | (5) |
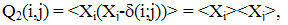 | (6) |
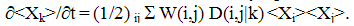 | (7) |
2. General Stochastic Approach to the Description of Coagulating Aerosol Systems
- The mesoscopic stochastic description is generally meant as an intermediate description level between treating microscopic (molecular) quantities (such as the position and pulse of each molecule) and macroscopic (thermodynamic) ones. The mesoscopic level deals with the distribution function (or stochastic process) for the order parameters whose averages are to be treated macroscopically as thermodynamic quantities. For an aerosol system one could point out such values as number of clusters in a unit volume, size of a given cluster treating them as the order parameters. Denote such an order parameter as q(t) without its concretization for a moment (of cource, q(t) can be readily understood as multycomponent vector as well). In the assumption of the Markovian character of a process the distribution function ω(q,t) satisfies the master equation of the general type (see, for example, Stratonovich, 1992):
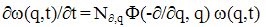 | (8) |
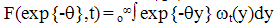 | (9) |
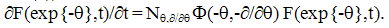 | (10) |
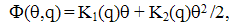 | (11) |
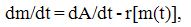 | (12) |
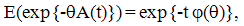 | (13) |
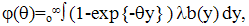 | (14) |
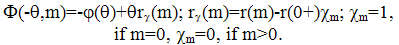 | (15) |
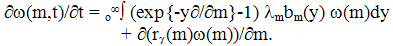 | (16) |
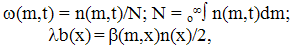 | (17) |
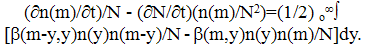 | (18) |
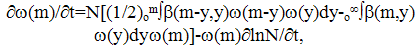 | (19) |
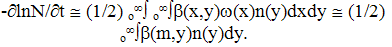 | (20) |
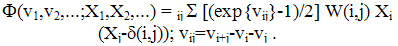 | (21) |
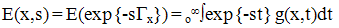 | (22) |
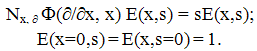 | (23) |
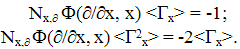 | (24) |
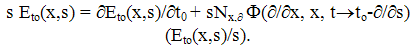 | (25) |
3. Generalization of the Storage Model
- The transform of kinetic potential Φ(x,q) is written, according to (Stratonovich,1992) as
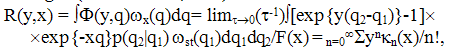 | (26) |
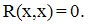 | (27) |
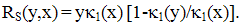 | (28) |
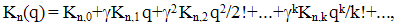 | (29) |
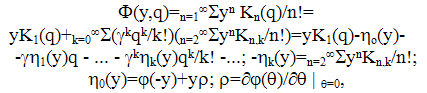 | (30) |
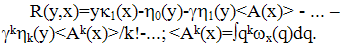 | (31) |
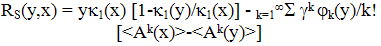 | (32) |
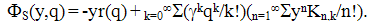 | (33) |
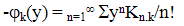 | (34) |
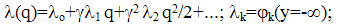 distribution function b(Δ,q) is related with function
distribution function b(Δ,q) is related with function 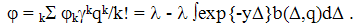 For example, we can set all functions φl(y)=φ(y)λl equal within a factor (proportional); this is the situation of the birth-and-death processes. This construction is to some extent analogous to that of (Prabhu, 1994) if one takes the modulating process I(t) (Prabhu, 1994) coinciding with the main process q(t).Substituting (33) into (10) we obtain the relation
For example, we can set all functions φl(y)=φ(y)λl equal within a factor (proportional); this is the situation of the birth-and-death processes. This construction is to some extent analogous to that of (Prabhu, 1994) if one takes the modulating process I(t) (Prabhu, 1994) coinciding with the main process q(t).Substituting (33) into (10) we obtain the relation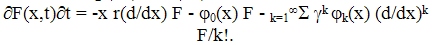 | (35) |
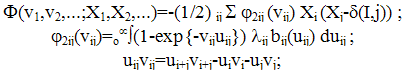 | (36) |
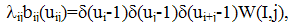 which coincides with (33) if γ=1, r=0, k=δ(k;2).Substituting (36) into (10) leads to
which coincides with (33) if γ=1, r=0, k=δ(k;2).Substituting (36) into (10) leads to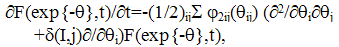 | (37) |
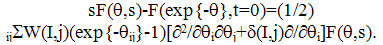 In (Lushnikov, 1978) the generating functional is written in the Smolukhovsky approximation when Xi→
In (Lushnikov, 1978) the generating functional is written in the Smolukhovsky approximation when Xi→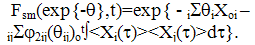 | (38) |
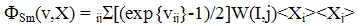 corresponds to the storage model with the input intensity proportional to
corresponds to the storage model with the input intensity proportional to 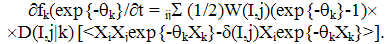 | (39) |
4. Application of the Storage Model to the Number of Monomers in a Cluster
- Consider the random number of monomers m in a single cluster (12)-(20). Combining (15)-(17) with (10) leads to
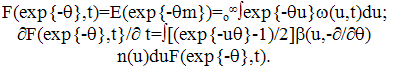 | (40) |
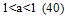 corresponds to fractional terms in the series (29) and fractional derivatives in (40) which is the manifestation of the fractal character of cluster formation (Nigmatullin, 1992). Thus the relations (15-20) used in (Ryazanov, 1991) correspond to the extension of the storage model with generalized Tailor series of fractional derivatives. The explicit form of Φ in (40) allows us to solve this equation specifying the kernel β(m,x). So, for β(m,x)=a=const taking into account n(u,t)=N ω(u,t) (17) one arrives at (set a=1 without loss of generality)∂Fa(θ)/∂ t = a (Fa(θ)-1) Fa(θ)/2;Fa(θ,t)=y(t)Fa(θ,t=0)/{1-Fa(θ,t=0)[(N(t=0)/2)ot∫y(τ)dτ+y(t)-1]}; y(t)=exp{-ot∫ N(τ)dτ}/2}.Stationary function F=1 corresponds to the delta-shaped peak of the probability density (for example, δ(m-M)). For (17) ω(x,t) = n(x,t)/N, F(exp{-θ},t) = n(θ)/N, n(θ) = o∞∫exp {-θx}n(x,t)dx. These results are in correspondence with the results of (Voloschuk, 1984) for β(m,x) =a =const. For the kernel β(m,x)=c(m+x) (40) get∂F(θ)/∂t = -cN [∂F(θ)/∂θ ((θ)-1) + MF(θ)/N]/2.For β(m,x)=cmx, ∂F(θ)/∂t=(c/2)N [∂F/∂θ + M/N] ∂F/∂θ.These equations lead to results which are close to those obtained from the Smolukhovsky equation (Voloschuk, 1984) but do not coincide with them completely. The question remains open about the approximation fitting better to the description of aerosols.The specification of λmbm(x) should lean upon the physical assumptions as to the physics of coagulation. The relation (17) corresponds to the assumption of instantaneous stirring of the system between successive coagulation acts resulting in quasihomogeneous state of the system and thus in the statistical identity of all clusters which (equation (20)) ensures the coincidence of the kinetic equation (16) with the Smolukhovsky equation (19) (if r=0 and (17) holds). One can detalize the model adding some function b1(x) to (17):
corresponds to fractional terms in the series (29) and fractional derivatives in (40) which is the manifestation of the fractal character of cluster formation (Nigmatullin, 1992). Thus the relations (15-20) used in (Ryazanov, 1991) correspond to the extension of the storage model with generalized Tailor series of fractional derivatives. The explicit form of Φ in (40) allows us to solve this equation specifying the kernel β(m,x). So, for β(m,x)=a=const taking into account n(u,t)=N ω(u,t) (17) one arrives at (set a=1 without loss of generality)∂Fa(θ)/∂ t = a (Fa(θ)-1) Fa(θ)/2;Fa(θ,t)=y(t)Fa(θ,t=0)/{1-Fa(θ,t=0)[(N(t=0)/2)ot∫y(τ)dτ+y(t)-1]}; y(t)=exp{-ot∫ N(τ)dτ}/2}.Stationary function F=1 corresponds to the delta-shaped peak of the probability density (for example, δ(m-M)). For (17) ω(x,t) = n(x,t)/N, F(exp{-θ},t) = n(θ)/N, n(θ) = o∞∫exp {-θx}n(x,t)dx. These results are in correspondence with the results of (Voloschuk, 1984) for β(m,x) =a =const. For the kernel β(m,x)=c(m+x) (40) get∂F(θ)/∂t = -cN [∂F(θ)/∂θ ((θ)-1) + MF(θ)/N]/2.For β(m,x)=cmx, ∂F(θ)/∂t=(c/2)N [∂F/∂θ + M/N] ∂F/∂θ.These equations lead to results which are close to those obtained from the Smolukhovsky equation (Voloschuk, 1984) but do not coincide with them completely. The question remains open about the approximation fitting better to the description of aerosols.The specification of λmbm(x) should lean upon the physical assumptions as to the physics of coagulation. The relation (17) corresponds to the assumption of instantaneous stirring of the system between successive coagulation acts resulting in quasihomogeneous state of the system and thus in the statistical identity of all clusters which (equation (20)) ensures the coincidence of the kinetic equation (16) with the Smolukhovsky equation (19) (if r=0 and (17) holds). One can detalize the model adding some function b1(x) to (17):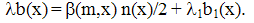 | (41) |
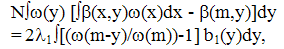 | (42) |
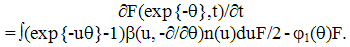 | (43) |
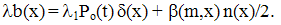 | (44) |
5. Conclusions
- One of the advantages of the stochastic storage model is the clear criteria stated for the existence of stationary states in a system (Ryazanov, 1991). Besides the external fields, the stationarity conditions are determined by such factors as the presence of sources and sinks of clusters, evaporation, condensation, splitting etc. For the stationary state of storage model the relations describing its behaviour are known in details. Specific for the aerosol system is the stationary state resulting from the pure coagulation. In this case the release of monomers is zero, and the system is far from being stationary. The input function also vanishes when all clusters form a single bulk cluster; the stationarity conditions remain undefined.The equations for the distribution function (16) and its Laplace transform (40), (43) encounter serious difficulties coming from the fractional derivatives; these difficulties however reflect the complex fractal (self-similar) behaviour of aerosol clusters. The fractional part of the derivative shows a fraction of systems states conserving during all the time of evolution. In (Nigmatullin, 1992) a broad class of systems was pointed out where one could expect the apparition of the fractional derivatives, coagulating systems belonging to this class as well. Such systems were referred to in (Nigmatullin, 1992) as "systems with residual memory" occupying an intermediate position between full memory systems, on one hand, and completely stochastic (Markovian) ones. Thus the application of purely Markovian processes (like storage or birth-and-death) to the description of coagulation is with necessity an approximation (generally speaking, the properties of a system to be either Markovian or non-Markovian were related in (Nigmatullin, 1992) to the presence of fractional derivatives in time; but the spatial fractional derivative is readily to appear in (40) likewise the first term of the right hand side of equation (16) if b(x)=cxν-1, 0<ν<1, 1≤m≤M; in the latter case however the spatial derivative on m can be transferred to the temporal variable and acts on the expression[∂n(m)/∂t-(n(m)∂N/∂t)/N2+c 1M∫yν-1dyn(m)/2N].A generic (typical one) distribution for the storage model is the gamma-distribution (like the Gaussian distribution occupying the same place in the diffusion models). The gamma distribution is known from experiments to fit well the real cluster-size distributions. The storage model is thus open to further detalization of cluster behaviour. In general the stochastic modelling opens vast perspectives for predicting the behaviour of real physical systems. An essential part of the research work in this direction must be the investigation of relations between mathematical abstractions coined by these methods and physical phenomena in a system as it is well known that the real processes in aerosols (as well as in any other natural system) are much more complicated than the mathematical models. Thats why the straightforward use of, e.g. storage models without stepwise and throught analysis of the approximations made is not warranted from faults.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML