-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(1): 39-45
doi: 10.5923/j.am.20110101.05
Hydromagnetic Unsteady Mixed Convection Flow Past an Infinite Vertical Porous Plate
B. K. Sharma 1, T. Chand 2, R. C. Chaudhary 2
1Department of Mathematics, Birla Institute of Technology & Science, Pilani, -333031, India
2Department of Mathematics, University of Rajasthan, Jaipur-302004, India
Correspondence to: B. K. Sharma , Department of Mathematics, Birla Institute of Technology & Science, Pilani, -333031, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
An approximate analysis of unsteady mixed convection flow of an electrically conducting fluid past an infinite vertical porous plate embedded in porous medium under constant transversely applied magnetic field is presented here. The periodic transverse suction velocity is applied to the surface due to which the flow becomes unsteady. The surface is kept at oscillating wall temperature. Analytical expressions for the transient velocity, temperature, amplitude and phase of the skin-friction and the rate of heat transfer are obtained and discussed in detail with the help of graphs, under different parameter values.
Keywords: Hydromagnetic Flow, Mixed Convection, Heat Transfer, Porous Plate
Cite this paper: B. K. Sharma , T. Chand , R. C. Chaudhary , "Hydromagnetic Unsteady Mixed Convection Flow Past an Infinite Vertical Porous Plate", Applied Mathematics, Vol. 1 No. 1, 2011, pp. 39-45. doi: 10.5923/j.am.20110101.05.
1. Introduction
- The problem laminar flow through a porous medium has become very important in recent years particularly in the fields of agricultural engineering to study the underground water resources, seepage of water in river beds, in chemical engineering for filtration and purification process; in petroleum technology to study the movement of natural gas, oil and water through the oil reservoirs. Oscillatory flows play an important role in technological field. The effects of free-stream oscillations on the flow past a semi-infinite plate were first studied by Lin[1] for finite amplitude and by Lighthill[2] for small amplitude oscillations. Lighthill studied this problem by employing momentum integral method. These results were confirmed experimentally by Hill and Stenning[3]. In many industrial, aeronautical engineering, atomic propulsion and space science, the oscillatory flow past an infinite vertical porous plate plays an important role. Free convection effects on the oscillatory flow past an infinite vertical porous plate with constant suction was initiated by Soundalgekar[4-5]. In both the papers, suction was assumed to be constant. However, in many engineering applications variable suction exists and the effect of variable suction on the flow past an infinite vertical porous plate was studied by Soundalgekar[6]. In all these studies, the plate temperature was assumed to be constant and hence isothermal.But in many industrial applications, the flow is steadyand in the upward direction and the plate temperature is oscillating. Such a study of the flow past an infinite vertical porous plate, under oscillating plate temperature and with constant or variable suction was presented by Soundalgekar et.al.[7]. The unsteady free convection flow past an infinite plate with constant suction and heat sources has been studied by Pop et.al.[8]. Raptis[9] studied the free convective flow through a porous medium bounded by an infinite vertical plate with oscillating plate temperature and constant suction. Raptis et.al.[10] further analysed the free convective flow through a highly porous medium bounded by an infinite vertical porous plate with constant suction when the free stream velocity oscillates about a mean constant value. Hooper et.al.[11] have presented the problem of mixed convection along an isothermal vertical plate in porous medium with injection and suction. Panda et. al.[12] considered the unsteady free convection flow and mass transfer past a vertical porous plate. Soundalgekar et. al.[13] considered the free convection effects on magnetohydrodynamics flow past an infinite vertical oscillating plate with constant heat flux. Chandran et. al.[14] studied the transient hydromagnetic natural convection on a vertical flat plate subject to heat flux. Sahoo et. al.[15] studied the magnetohydrodynamic unsteady free convection flow past an infinite vertical plate with constant suction and heat sink. Heat and mass transfer in magnetohydrodynamics flow of a viscous fluid past a vertical plate under oscillatory suction velocity has been studied by Singh et. al.[16]. Helmy[17] studied the magnetohydrodynamics unsteady free convection flow past a vertical porous plate. Acharya et. al.[18] made a systematic analysis of magnetic field effects on the free-convective and mass transfer flow through porous medium with constant suction and constant heat flux. Ahmed et. al.[19] extended Acharya’s[18] works to unsteady case by considering a uniform motion of the plate. Jaiswal et. al.[20] further extended his problem. Unsteady free and forced convection magnetohydrodynamics flow past an infinite vertical porous plate with variable suction and oscillating plate temperature. Sharma et. al.[21-22] considered the hydromagnetic unsteady mixed convection and mass transfer flow past a vertical porous plate immersed in a porous medium. Recently, Effects of fluctuating surface temperature and concentration on unsteady convection flow past an infinite vertical plate with constant suction discussed by Sharma et. al[23].In the above stated studies the flows with the oscillatory suction velocity and with the influence of uniform magnetic field are not considered while such flows are encountered in geophysical problems, astrophysical problems, soil sciences and so on. Therefore, the present investigation is to study the effects of permeability and magnetic field as the flow past a vertical plate embedded on a porous medium and subjected to oscillating suction and temperature field. It is found that the permeability and magnetic field have significant effects on the flow and heat transfer.
2. Mathematical Formulation
- We consider the flow of an electrically conducting viscous incompressible fluid through a porous medium bounded by an infinite vertically porous flat plate. The x*-axis is taken along the plate, being the vertically upward direction of the flow and y*-axis is taken perpendicular to the plate directed into the fluid. The fluid flows with uniform free stream velocity U. A uniform magnetic field is imposed along the y*-axis. The induced magnetic field is negligible which is possible on a laboratory scale. Since the plate is considered infinite in the x*-direction, hence all the fluid properties are independent of x*. Let u*, v* be the fluid velocities along x*, y*-axes respectively and the plate temperature T* is oscillating about a non-zero plate temperature
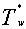 . The variation of the suction velocity distribution of the form
. The variation of the suction velocity distribution of the form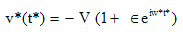 | (1) |
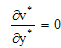 | (2) |
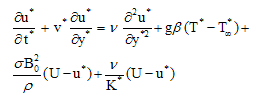 | (3) |
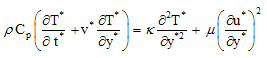 | (4) |
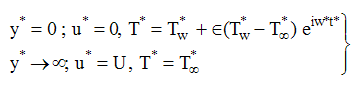 | (5) |
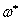 is the frequency of the plate temperature oscillations and
is the frequency of the plate temperature oscillations and 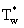 is the temperature of the plate. The subscripts w and ∞ denotes physical quantities at the plate and in the free stream respectively.Introducing the following non-dimensional quantities in equations (2) to (4)
is the temperature of the plate. The subscripts w and ∞ denotes physical quantities at the plate and in the free stream respectively.Introducing the following non-dimensional quantities in equations (2) to (4)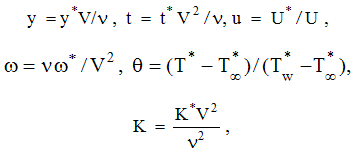 the Permeability parameter
the Permeability parameter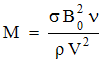 the Hartmann number
the Hartmann number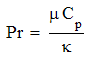 the Prandtl number
the Prandtl number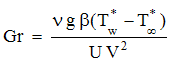 the Grashof number
the Grashof number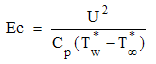 the Eckert number, we get
the Eckert number, we get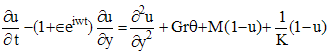 | (6) |
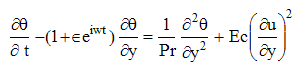 | (7) |
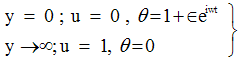 | (8) |
3. Solution
- When the amplitude ∈ < < 1 is very small, in order to solve these coupled non-linear differential equations, we assume the solution in the neighbourhood of the plate that the unsteady flow is superimposed on the mean steady flow is represented mathematically of the form
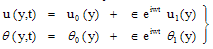 | (9) |
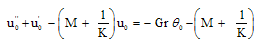 | (10) |
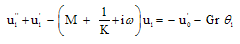 | (11) |
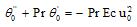 | (12) |
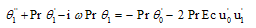 | (13) |
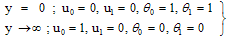 | (14) |
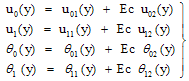 | (15) |
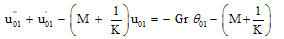 | (16) |
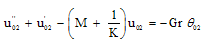 | (17) |
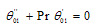 | (18) |
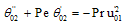 | (19) |
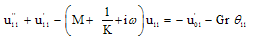 | (20) |
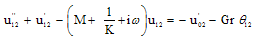 | (21) |
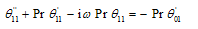 | (22) |
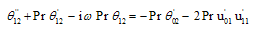 | (23) |
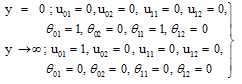 | (24) |
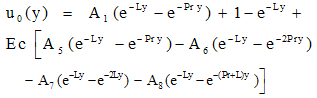 | (25) |
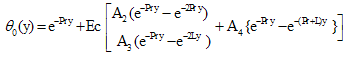 | (26) |
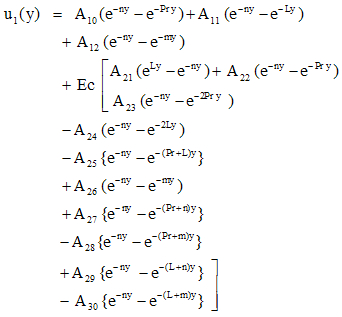 | (27) |
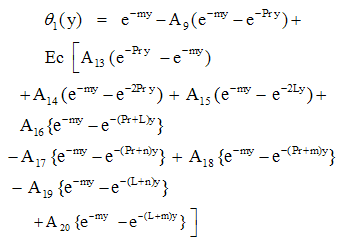 | (28) |
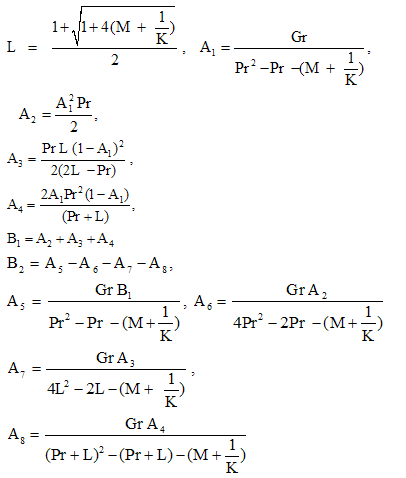
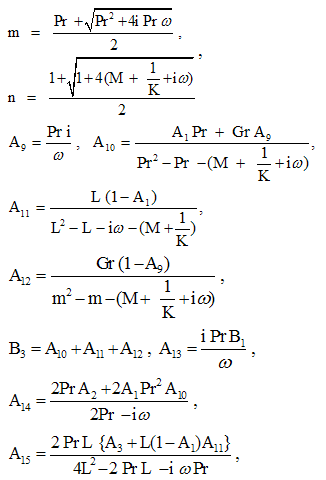
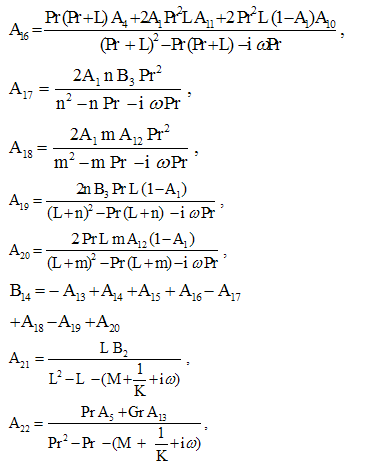
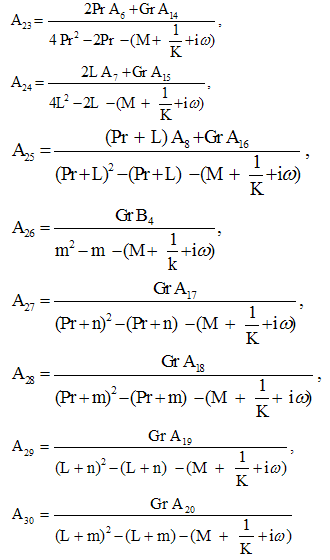
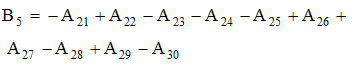 Substituting u0, θ0, u1 and θ1 in equation (9) for u and θ, we get the expressions for the main flow velocity and temperature, which can be expressed in terms of the fluctuating parts as
Substituting u0, θ0, u1 and θ1 in equation (9) for u and θ, we get the expressions for the main flow velocity and temperature, which can be expressed in terms of the fluctuating parts as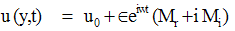 | (29) |
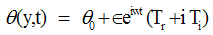 | (30) |
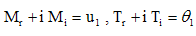 For ωt = π/2, we can obtain the expressions for the transient velocity and temperature profiles as
For ωt = π/2, we can obtain the expressions for the transient velocity and temperature profiles as 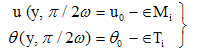 | (31) |
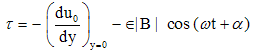 | (32) |
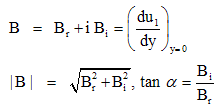 | (33) |
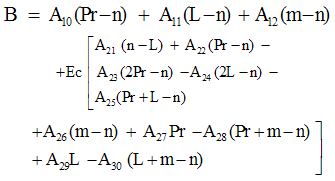 | (34) |
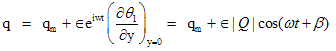 | (35) |
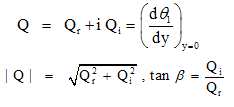 | (36) |
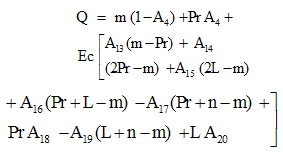 | (37) |
4. Discussion of Results
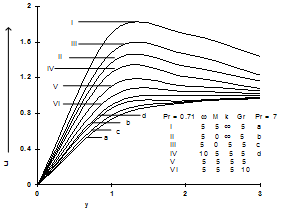 | Figure 1. Transient velocity for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
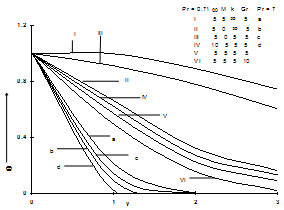 | Figure 2. Transient temperature for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
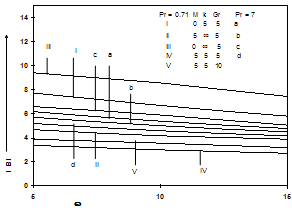 | Figure 3. The amplitude of skin-friction for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
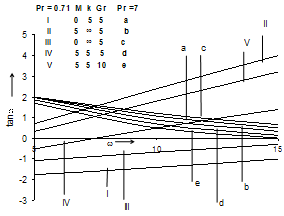 | Figure 4. Phase of skin-friction for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
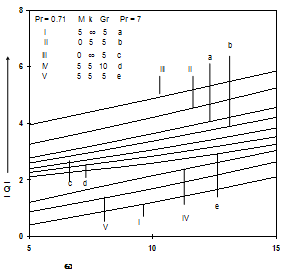 | Figure 5. The amplitude of the rate of heat transfer for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
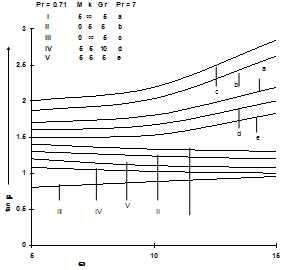 | Figure 6. Phase of rate of heat transfer for ∈ = 0.2, Ec = 0.1 and ωt = π/2. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML