-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(1): 28-38
doi: 10.5923/j.am.20110101.04
Characterizing Hysteresis Nonlinearity Behavior of SMA Actuators by Krasnosel’skii-Pokrovskii Model
M. R. Zakerzadeh 1, H. Sayyaadi 1, M. A. Vaziri Zanjani 2
1School of Mechanical Engineering, Sharif University of Technology, Tehran, 11155-9567, Iran
2School of Aerospace Engineering, Amirkabir University of Technology, Tehran, 15875-4413, Iran
Correspondence to: H. Sayyaadi , School of Mechanical Engineering, Sharif University of Technology, Tehran, 11155-9567, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Krasnosel’skii-Pokrovskii (KP) model is one of the great operator-based phenomenological models which is used in modeling hysteretic nonlinear behavior in smart actuators. The time continuity and the parametric continuity of this operator are important and valuable factors for physical considerations as well as designing well-posed identification methodologies. In most of the researches conducted about the modeling of smart actuators by KP model, especially SMA actuators, only the ability of the KP model in characterizing the hysteretic behavior of the actuators is demonstrated with respect to some specified experimental data and the accuracy of the developed model with respect to other data is not validated. Therefore, it is not clear whether the developed model is capable of predicting hysteresis minor loops of those actuators or not and how accurate it is in this prediction task. In this paper the accuracy of the KP model in predicting SMA hysteresis minor loops as well as first order ascending curves attached to the major hysteresis loop are experimentally validated, while the parameters of the KP model has been identified only with some first order descending reversal curves attached to the major loop. The results show that, in the worst case, the maximum of prediction error is less than 18.2% of the maximum output and this demonstrates the powerful capability of the KP model in characterizing the hysteresis nonlinearity of SMA actuators.In order to have continuous operator rather than jump discontinuities like the Preisach operator, Krasnosel’skii- Pokrovskii[12] allows the Preisach operators to be any reasonable functions. The elementary operator of the KP model which is referred to as the KP kernel, a special case of a so called generalized play operator, is a continuous function on the Preisach plane and has minor loops within its major loop. Let P be the Preisach plane over which hysteresis occurs:
Keywords: Krasnosel’skii-Pokrovskii Hysteresis Model, SMA Actuators
Cite this paper: M. R. Zakerzadeh , H. Sayyaadi , M. A. Vaziri Zanjani , "Characterizing Hysteresis Nonlinearity Behavior of SMA Actuators by Krasnosel’skii-Pokrovskii Model", Applied Mathematics, Vol. 1 No. 1, 2011, pp. 28-38. doi: 10.5923/j.am.20110101.04.
Article Outline
1. Introduction
- In systems with hysteretic behavior, like piezoelectics, piezoceramics, magnetostrictives and shape memory alloys, the input-output relationship is a multi-branch nonlinearity for which branch-to-branch transitions occur after input exterma[1]. It means that the output value is a function not only of the current input, but also of the previous inputs and/or the initial value. Indeed, at any accessible point in the input-output diagram there are many curves that may rep-resent the future behavior of the system. Each of these curves depends on the sequence of past extermum values of the input[2]. Therefore, mathematical modeling as well as controller design of these systems is a complex and difficult task.Since un-modeled hysteresis causes inaccuracy in trajectory tracking and decreases the performance of the control systems, an accurate modeling of hysteresis behavior for performance evaluation and identification as well as controller design is essentially needed[3]. Therefore, it is necessary to develop hysteresis models that not only identification of the model parameters, to adapt the model to the real hysteretic nonlinearity, can easily and precisely be per-formed but also are suitable for real time control and compensation system design. A number of models have been proposed to capture the observed hysteretic characteristics of smart actuators, which could be classified into physics-based hysteresis models and phenomenological hysteresis models[4]. Physics-based models are generally come from the underlying physics of hysteresis and are combined with empirical factors to de-scribe the observed characteristics[5-7]. However, these models have limited range of applicability, as the physical basis of some of the hysteresis characteristics is not completely understood[8]. Furthermore, considerable effort is required in identifying and tuning the model parameters to accurately describe the hysteresis nonlinearity. Another major drawback of these physical models is that they are specific to a particular system, and this implies separate controller design techniques for each system[9]. Since the early 1970's, systematic mathematical analyses of the hysteresis as a general nonlinear behavior, from purely phenomenological viewpoint, have been carried out[10]. Phenomenological models are based on the phenomeno- logical nature and mathematically describe the observed phenomenon without necessarily providing physical insight into the problems. The most important phenomenological hysteresis models include operator based hysteresis models and differential equation-based hysteresis models[11]. Preisach model[2], Krasnosel’skii-Pokrovskii model[1], and Prandtl-Ishlinskii model[12] are some important operator- based hysteresis models while Duhem model, Bouc-Wen model and Jiles-Atherton model[13] are most widely used differential equation-based hysteresis models. Choosing a proper phenomenological model among the mentioned models is a task of crucial importance since the mathematical complexity of the identification and inversion problem depend directly on the phenomenological modeling method and strongly influences the practical use of the design concept[14]. Furthermore, the accuracy of the modeling method in characterizing system hysteretic behavior consequently affects the whole compensator design task. For example, Philips[15] compared the computation results from the Jiles-Atherton model and the Preisach model. It was found that the identification of the parameters in the Jiles-Atherton model requires less measurement while the Preisach model fits the hysteresis loop better.Modeling the SMA actuators by each of the mentioned groups has their own advantages and disadvantages. Models of the first group are better suited to deal with the effects of complex multiaxial thermomechanical loading paths and cyclic effects of SMAs, due to the flexibility of introducing internal state variables in their formulation. However, these classical models usually give poor predictions to the minor loop hysteretic response[16]. Phenomenological models, on the other hand usually give excellent predictions of the minor loop behavior if the loading path does not change.Among the phenomenological models, the Preisach model has found extensive application for modeling hysteresis in SMAs and other smart actuators[17-18,2]. In Preisach modeling technique, overall system with hysteresis behavior is modeled by weighted parallel connections of non-ideal relays termed as Preisach elementary operators. Output of these Preisach operators would be only +1 or –1 (zero in some models). Every elemental operator as a nonlinear operator consists of two parameters; upper and lower switching values of input respectively. Along with the set of Preisach operators is an arbitrary weight function, called the Preisach Density Function (PDF), which works as a local influence of each operator in overall hysteresis model.The time continuity of an operator is important for physical considerations, while the parametric continuity is important for designing well-posed identification methodologies[19]. However, the kernel of the Preisach operator has no continuity in time space or in parameter space. In[20] Banks et.al, introduced the smoothed version of the Preisach operator. To construct the continuous preisach operator in time space, they first define a smoothed delayed operator, each of whose ascending and descending branches are continuous. This continuous Preisach model yields a continuous output hysteresis, even for measures that are not absolutely continuous with respect to Lebesgue measure. However, this operator was also not continuous in parametric space.In order to have continuous operator in time domain as well as in parameter space Krasnosel’skii-Pokrovskii[12] allowed the Preisach kernels to be any reasonable functions. The KP type operator, a special case of a so-called generalized play operator, is a hysteretic operator treating continuous branches rather than jump discontinuities like in the Preisach operator. This kind of generalization finally separates the Preisach model from its physical meaning and ends up with a purely mathematical and phenomenological operator[21]. This generalized Preisach model has been further investigated and applied in[20], where kernels other than non-ideal relay operators are employed to achieve some mathematical properties. Banks et al.[20] proved that K-P operators are continuous in time as well as in parameter space. They also compared the physical and mathematical properties of K-P operator with those of the classical Preisach operator.Since the original integral form of the KP model easily cannot numerically and practically implemented, the linearly parameterized KP model usually applied. This stems from these reasons that it is very difficult to formulate suitable weighting function which is double-integrable and also it is impossible to describe the outputs of the kernel as continuous functions due to nonlinearity of the kernel[22]. In this method, a finite number of the kernel functions is utilized and each kernel function itself stands for a reasonable approximation of actual hysteresis curves of the actuator.There are many experimental researches about modeling SMA actuators by Preisach model in order for evaluating and predicting their behaviors but using the KP model in this area is much less. Webb et al.[23] presented an adaptive hysteresis model, which was a linearly parameterized version of the KP hysteresis model. This model can be updated continuously by using adaptive method so that it can describe the hysteresis behavior of an SMA wire actuator successfully under extended disturbances and various loading conditions. They provided laboratory evidence of the success of the proposed adaptive KP model for feedback control of an SMA wire actuator. Since the proposed KP hysteresis model can adaptively identify, it is robust in the presence of large measurement errors. Moreover, by computing the inverse of it, the effect of the hysteresis in SMA actuator can be actively compensated. Koh[24] used a similar adaptive control technique with a KP hysteresis operator. It was shown that the inverse of hysteresis behavior also has qualitatively the same characteristics of hysteresis. Therefore, in order to evade the computation of the inverse of the KP model, the inverse model with KP hysteresis operator was directly used. Finally, the result of the proposed controller is experimentally compared with ones of a PI controller.In[25] Galinaitis demonstrated the ability of KP model to model hysteresis of piezoelectric actuator and also the effectiveness of the inverse compensation to minimize hysteresis. In addition using the experimental data collected from a piezoelectric actuator with scalar hysteresis, the accuracy of the forward model was also demonstrated. Furthermore, the feasibility of using inverse of KP model to provide the necessary compensation for reducing positioning error created by hysteresis was displayed. In most of the researches conducted about the modeling of SMA actuators by KP model, only the ability of the KP model in characterizing the hysteretic behavior of the actuators is demonstrated with respect to some specified experimental data and the accuracy of the developed model with respect to other data is not validated. In other words only the parameters of KP model are identified in order to adapt the model response to the real hysteretic nonlinearity with some specific experimental data and finally the outputs of the obtained KP are compared with those same data. Therefore, it is not clear whether the developed model is capable in predicting hysteresis minor loops of SMA materials or not and how its accuracy in this prediction task is. Some of the shortcomings of the mentioned studies are due to the fact that the tested actuator was not available in the laboratory and therefore further experimental tests were not performable. Also, if the inverse of the KP model is a candidate for hysteresis nonlinearity compensation using an open loop feedforward controller, it is important to know how accurate the developed model would model the ob-served input-output relation and determine whether using a feedback controller is essential or not.In this paper, first the parameterized KP model is identified by some experimentally measured data obtained from an experimental test set-up consisting of a flexible beam actuated by a shape memory alloy wire. The training data are the data of first order descending curve attached to the ascend branch of the major hysteresis loop. The parameters of the KP model are identified by least square method in order to adapt the model response to the real hysteretic nonlinearity. Then the accuracy of the developed KP model with known parameters in predicting nonlinear hysteretic behavior of first order ascending curves and higher order minor loops, is validated with some other experimental data. Although the model has been trained with data of first order descending reversal curves, it has good power in behavior prediction of first order ascending curves as well as higher order minor loops.
2. Krasnosel’ski-Pokrovkii (KP) Hysteresis Model
- Preisach model is a famous hysteresis identification technique which was first introduced on the base of phenomenological analysis of ferromagnetic materials by German physicist F. Preisach in almost 75 years ago [26]. The Russian mathematician, Krasnoselskii, in 1970 represented Preisach model into a pure formulized mathematical form in which hysteresis is modeled by linear combination of hysteresis operators[12]. Mathematical form of the classical Preisach model can be sketched by equation as follows:
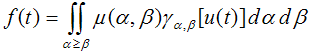 | (1) |
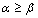 ) parameters as upper and lower switching values respectively (see figure. 1). Output of elementary operators would be only +1 or –1 (zero in some models). In (1), μ(α,β) is density function value or Preisach function corresponding to α and β which should be determined by use of some experimentally measured data.
) parameters as upper and lower switching values respectively (see figure. 1). Output of elementary operators would be only +1 or –1 (zero in some models). In (1), μ(α,β) is density function value or Preisach function corresponding to α and β which should be determined by use of some experimentally measured data.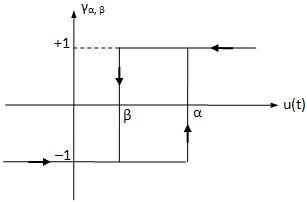 | Figure 1. Preisach elementary operator. |
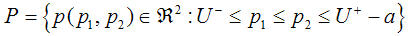 | (2) |
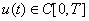 respectively. The positive Parameter a is the rise constant of the kernel and is chosen based on the discrete implementation explained later.If C[0,T] denotes the space of continuous piecewise monotone functions on the interval [0,T], then the elementary KP hysteresis operator is a mapping as following:
respectively. The positive Parameter a is the rise constant of the kernel and is chosen based on the discrete implementation explained later.If C[0,T] denotes the space of continuous piecewise monotone functions on the interval [0,T], then the elementary KP hysteresis operator is a mapping as following: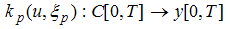 where ξp , parameterized by p, represents the initial condition of the kernel and memory the previous extreme output of kernel, and y[0,T] is the function space of output. Indeed, for a specified u(t) the KP operator Kp(u, ξp) maps points p(p1,p2) to the interval [-1,1] and is given by:
where ξp , parameterized by p, represents the initial condition of the kernel and memory the previous extreme output of kernel, and y[0,T] is the function space of output. Indeed, for a specified u(t) the KP operator Kp(u, ξp) maps points p(p1,p2) to the interval [-1,1] and is given by: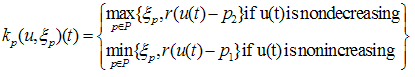 | (3) |
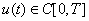 , the KP kernel has continuity in time domain as well as in parameter space. These advantages enable the KP model as a more effective practical model to formulate and model the smart material hysteresis behavior. The nondecreasing continuous ridge function can get any form but it is popular to select it as a continuous piecewise linear function defined as following:
, the KP kernel has continuity in time domain as well as in parameter space. These advantages enable the KP model as a more effective practical model to formulate and model the smart material hysteresis behavior. The nondecreasing continuous ridge function can get any form but it is popular to select it as a continuous piecewise linear function defined as following: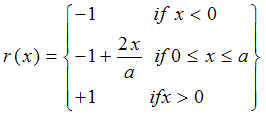 | (4) |
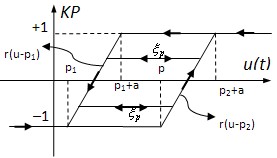 | Figure 2. KP elementary operator. |
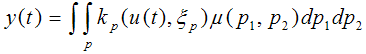 | (5) |
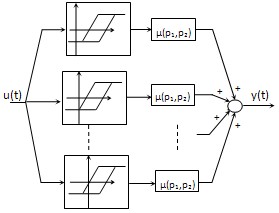 | Figure 3. KP model as parallel connection of weighted kernels. |
3. Linearly Parameterized KP Hysteresis Model
- Although the first form of the KP model was first presented as equation (5) but for numerical implementing it on a real system or process there are some difficulties to calculate the hysteresis output. First of all, due to the nonlinearity nature of the kernel it is impossible to describe the outputs of the kernel as a continuous function. Second, it is a difficult task to formulate a proper weighting function
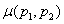 which is double-integrable over the Preisach plane[22]. In order to numerically implementing the KP model, equation (5) must be transformed into parameterized form by dividing the Preisach plane P, as shown in figure. 4, into a mesh grid. If the Preisach plane P is uniformly divided by l horizontal lines and l vertical lines, then the number of small cells representing the Preisach plane P is N=0.5(l+2)(l+1). If l is selected large enough, the discretization becomes very fine and the cells become very small resulting to the parameterized KP model acts like the integral KP model. However, the computational cost become expensive forcing us to consider a suitable l. The coordinates
which is double-integrable over the Preisach plane[22]. In order to numerically implementing the KP model, equation (5) must be transformed into parameterized form by dividing the Preisach plane P, as shown in figure. 4, into a mesh grid. If the Preisach plane P is uniformly divided by l horizontal lines and l vertical lines, then the number of small cells representing the Preisach plane P is N=0.5(l+2)(l+1). If l is selected large enough, the discretization becomes very fine and the cells become very small resulting to the parameterized KP model acts like the integral KP model. However, the computational cost become expensive forcing us to consider a suitable l. The coordinates 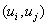 of lower-left nodes of each cells expressed as:
of lower-left nodes of each cells expressed as: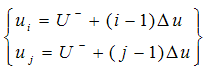 | (6) |
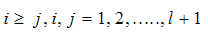 | (7) |
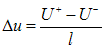 | (8) |
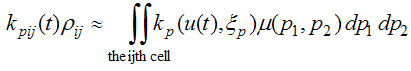 | (9) |
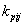 is the kernel associated with the lower left node of the cell and
is the kernel associated with the lower left node of the cell and 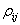 is called the lumped density of the ijth cell to its lower-left node with coordinate
is called the lumped density of the ijth cell to its lower-left node with coordinate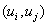 . By combining equation (5) and (9) one has:
. By combining equation (5) and (9) one has: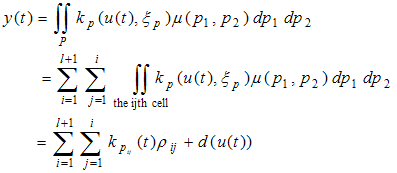 | (10) |
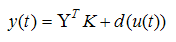 | (11) |
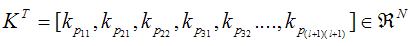 | (12) |
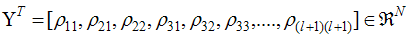 | (13) |
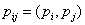 are calculated and as stated before the value of the rise constant, a, of equation (4) should be selected as Δu. Since the kernels
are calculated and as stated before the value of the rise constant, a, of equation (4) should be selected as Δu. Since the kernels 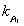 are characterized by
are characterized by 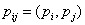 and the rise constant, a, then they can easily be obtained afterward. Finally, by matching the experimental data to the simulated results, using an optimization method like least square method, the density vector Y can be obtained. After identification process and by using this calculated density vector, the simulated output corresponding to any input signal can easily be computed by using equation (11).
and the rise constant, a, then they can easily be obtained afterward. Finally, by matching the experimental data to the simulated results, using an optimization method like least square method, the density vector Y can be obtained. After identification process and by using this calculated density vector, the simulated output corresponding to any input signal can easily be computed by using equation (11).
|
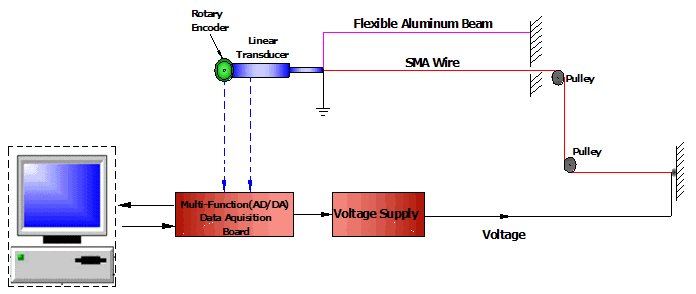 | Figure 5. Schematic of the cantilever flexible beam set-up actuated by a SMA wire. |
4. Experimental Test Set-up
- Figures 5 and 6 present a PC-based experimental test set-up and its associated instruments which is used to investigate the capability of the linearly parameterized KP hysteresis model in prediction of a flexible beam behavior under a SMA wire actuation. of the beam does not change during cooling and heating process.
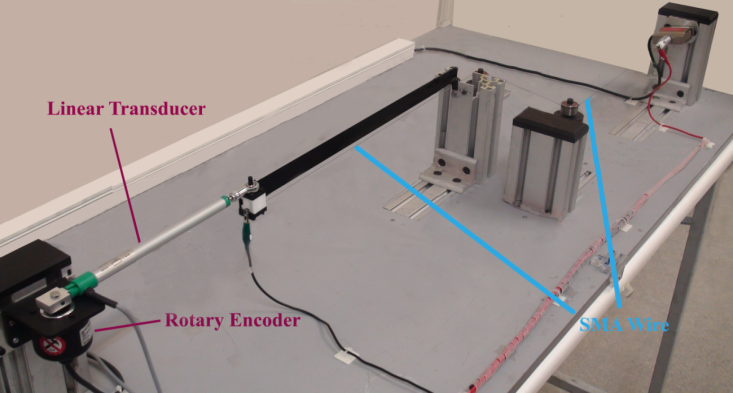 | Figure 6. Experimental test set-up used for verification of the current analysis results. |
 | Figure 7. Top view of the deformed beam after the wire actuation. |
5. Identification and Validation Processes
- The input voltage applied to the SMA actuator in the training process is a slow decaying ramp signal and is shown in figure. 8. The rate of change of the input voltage is selected so small in order to allow the temperature to stabilize, as in the steady state temperature will be determined by applied electrical voltage. In the training process of the linearly parameterized KP hysteresis model, 439 data set, consist of the major loop and 10 first order descending reversal curves attached to the major loop, is used. For identification density vector of linearly parameterized KP hysteresis model following values are used:
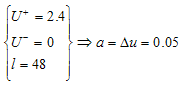 It should be mentioned here that if the wiping-out and congruency properties are valid, then it does not matter which transition curves are used for modeling of hysteresis nonlinearity by the Preisach or KP model and all of them will theoretically lead to the same result[2]. However, from the practical viewpoints, the first-order transition curves have some clear merits. First, it is easier to get these curves experimentally rather than higher-order transition curves. Second, measurements of these curves start from a well-defined state – the state of negative (or positive) saturation[2]. We performed the wiping out and congruency tests in this research (not reported here) and it is concluded that, same as the result of[18], the wiping-out property holds to a significant extent for our SMA actuator, while the congruency property is not completely satisfied. However, the deviation is not significant. It is worth mentioning that since the output of the system (tip deflection of the beam) never gets negative values, the ridge function (equation (4)) is corrected as following:
It should be mentioned here that if the wiping-out and congruency properties are valid, then it does not matter which transition curves are used for modeling of hysteresis nonlinearity by the Preisach or KP model and all of them will theoretically lead to the same result[2]. However, from the practical viewpoints, the first-order transition curves have some clear merits. First, it is easier to get these curves experimentally rather than higher-order transition curves. Second, measurements of these curves start from a well-defined state – the state of negative (or positive) saturation[2]. We performed the wiping out and congruency tests in this research (not reported here) and it is concluded that, same as the result of[18], the wiping-out property holds to a significant extent for our SMA actuator, while the congruency property is not completely satisfied. However, the deviation is not significant. It is worth mentioning that since the output of the system (tip deflection of the beam) never gets negative values, the ridge function (equation (4)) is corrected as following: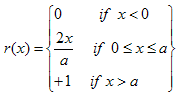 The switching values of the descending reversal curves are selected as: [2.4, 2, 1.8, 1.75, 1.7, 1.65, 1.6, 1.55, 1.5, 1.45, and 1.4] (volt). For switching values less than 1.4 (volt), the change in the beam deflection is not considerable. The experimental input-output hysteresis loops of the flexible beam with SMA wire actuator, under the abovementioned input voltage is shown in figure. 9.
The switching values of the descending reversal curves are selected as: [2.4, 2, 1.8, 1.75, 1.7, 1.65, 1.6, 1.55, 1.5, 1.45, and 1.4] (volt). For switching values less than 1.4 (volt), the change in the beam deflection is not considerable. The experimental input-output hysteresis loops of the flexible beam with SMA wire actuator, under the abovementioned input voltage is shown in figure. 9. 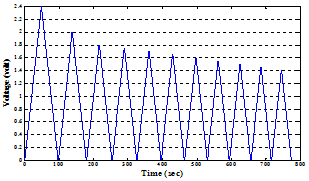 | Figure 8. The decaying ramp input voltage applied in the training process. |
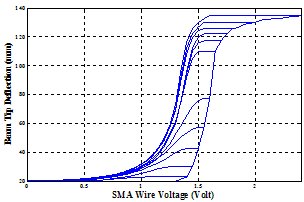 | Figure 9. Experimental data of hysteresis behavior between the beam tip deflection and the SMA wire voltage in the training process. |
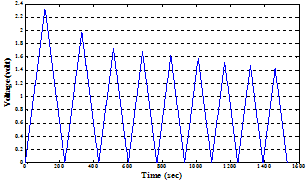 | Figure 10. The decaying ramp input voltage applied in the first validation process. |
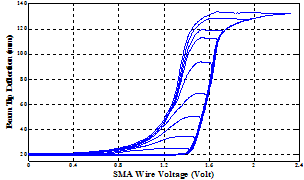 | Figure 11. Experimental data of hysteresis behavior between the beam tip deflection and the SMA wire voltage in the first validation process. |
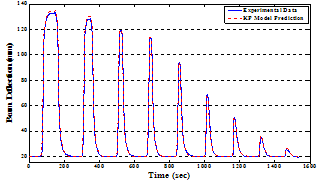 | Figure 12. Comparison between the displacement response of the linearly parameterized KP hysteresis model and the measured data of the flexible smart beam in the first validation process. |
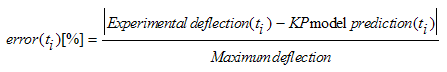 then the effectiveness of the linearly parameterized KP hysteresis can also be seen from the percentage of absolute error (%) plot, in the time domain, presented in figure. 13. As it is clear from these figures, the linearly parameterized KP hysteresis model has excellent ability in predicting the beam behavior under the voltage actuations which are same as ones implemented in the training process. In order to show this property more clearly, the maximum, mean and mean squared values of the absolute error are also presented in
then the effectiveness of the linearly parameterized KP hysteresis can also be seen from the percentage of absolute error (%) plot, in the time domain, presented in figure. 13. As it is clear from these figures, the linearly parameterized KP hysteresis model has excellent ability in predicting the beam behavior under the voltage actuations which are same as ones implemented in the training process. In order to show this property more clearly, the maximum, mean and mean squared values of the absolute error are also presented in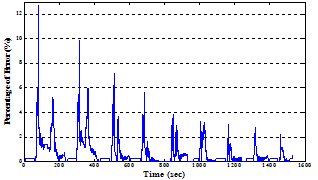 | Figure 13. Time history of percentage of error in the first validation process. |
|
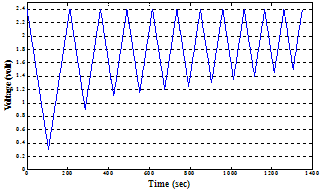 | Figure 14. The input voltage profile applied in the second validation process. |
|
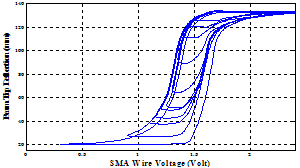 | Figure 15. Experimental data of hysteresis behavior between the beam tip deflection and the SMA wire voltage in the second validation process. |
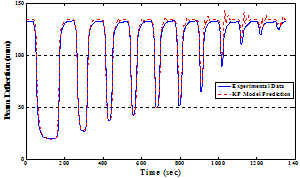 | Figure 16. Comparison between the displacement response of the linearly parameterized KP hysteresis model and the measured data of the flexible smart beam in the second validation process. |
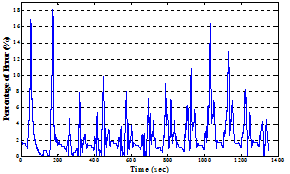 | Figure 17. Time history of absolute error between linearly parameterized KP hysteresis model and experimental measured displacement responses in the second validation process. |
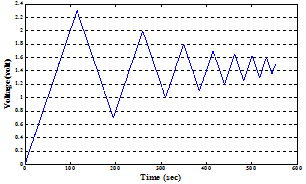 | Figure 18. The input voltage profile applied in the third validation process. |
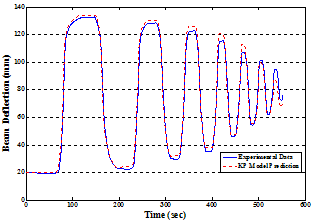 | Figure 19. Comparison between the displacement response of the linearly parameterized KP hysteresis model and the measured data of the flexible smart beam in the third validation process. |
|
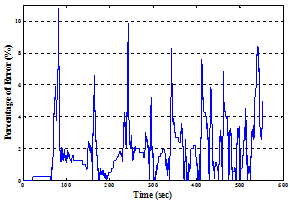 | Figure 20. Time history of absolute error between the linearly parameterized KP hysteresis model and experimental measured displacement responses in the third validation process. |
6. Conclusions
- The Preisach model is one of the powerful operator-based phenomenological models which is used in modeling complex hysteretic nonlinear behavior in shape memory alloy actuators. In order to have continuous operator in time domain as well as in parameter space Krasnosel’ skii- Pokrovskii [12] allows the Preisach kernels to be any reasonable functions. The KP type operator, a special case of a so-called generalized play operator, is a hysteretic operator treating continuous branches rather than jump discontinuities like in the Preisach operator.Since the original integral form of the KP model easily cannot numerically and practically implemented, the linearly parameterized KP model usually applied. In this method, a finite number of the kernel functions is utilized and each kernel function itself stands for a reasonable approximation of actual hysteresis curves of the actuator.In most of the researches conducted about the modeling of SMA actuators by KP model, only the ability of the KP model in characterizing the hysteretic behavior of the actuators is demonstrated with respect to some specified experimental data and the accuracy of the developed model with respect to other data is not validated. In other words only the parameters of KP model are identified in order to adapt the model response to the real hysteretic nonlinearity with some specific experimental data and finally the outputs of the obtained KP are compared with those same data. Therefore, it is not clear whether the developed model is capable of predicting hysteresis minor loops of SMA materials or not and how its accuracy in this prediction task is. This issue is important from this point of view that if the inverse of the KP model is a candidate for hysteresis nonlinearity compensation using an open loop feedforward controller, it is important to know how accurate the developed model would model the observed input-output relation and determine whether using a feedback controller is essential or not. In this paper, first the parameterized KP model is identified by some experimental data obtained from an experimental test set-up consisting of a flexible beam actuated by a shape memory alloy wire. The training data are 439 data set, consist of the major loop and 10 first order descending reversal curves attached to the major loop. The parameters of the KP model are identified by least square method in order to adapt the model response to the real hysteretic nonlinearity. Then the accuracy of the developed KP model with known parameters in predicting nonlinear hysteretic behavior of first order ascending curves and higher order minor loops, is validated with some other experimental data. Although the model has been trained with data of first order descending reversal curves, it has good power in behavior prediction of first order ascending curves as well as higher order minor loops. The maximum prediction error of the developed model in characterizing the first order ascending curves and higher order minor loops are, respectively, 18.2% and 10.8% of the maximum output. In order to achieve better results more data should be applied. According to result of this paper and it is a good candidate for predicting the hysteresis nonlinearity of SMA actuators as well as a feedforward controller to compensate the hysteretic nonlinearity behavior of SMA actuated structures.
ACKNOWLEDGEMENTS
- The authors would like to thank Eng. Ali Vahedi, manager of Nanotechnology and Smart Structure Group in HESA aeronautical research center for his great supports. Thanks are also extended to HESA Simulators & Flight Training Systems for helping with the construction of the experimental test set-up used in this paper. Authors also appreciate research scholar Hamid Salehi for many valuable comments.
References
| [1] | M. Brokate and J. Sprekels, Hysteresis and Phase Transitions, New York, Springer, 1996. |
| [2] | I.D. Mayergoyz, Mathematical Models of Hysteresis, New York, Elsevier, 2003. |
| [3] | M. R. Zakerzadeh, M. Firouzi, H. Sayyaadi, S. B. Shouraki, “Hysteresis nonlinearity identification using new preisach based artificial neural network approach,” Hindawi Publishing Corporation, Journal of Applied Mathematics, vol. 2011, Article ID 458768, 22 pages. |
| [4] | Xiaobo TAN and Ram V. Iyer, “Modeling and control of hysteresis,” IEEE Control Systems Magazine, February 2009, vol. 3, pp. 26-29. |
| [5] | V. Basso, P.S. Carlo, L.B. Martino, “Thermodynamic aspects of first order phase transformations with hysteresis in magnetic materials”, Magn Magn Mater, 2007, 316(2):262–8. |
| [6] | Cao S, Wang B, Yan R, Huang W, Yang Q, “Optimization of hysteresis parameters for the Jiles–Atherton model using a genetic algorithm”, IEEE Trans Appl Supercon, 2004; 14:1157–60. |
| [7] | Leite JV, Avila SL, Batistela NJ, Carpes WP, Sadowski Jr N, Kuo-Peng P, et al, “Real coded genetic algorithm for Jiles–Atherton model parameters identification”, IEEE Trans Magn, 2004;40:888–91. |
| [8] | K. K. Ahn, N. B. Kha., “Modeling and control of shape memory alloy actuators using Preisach model, genetic algorithm and fuzzy logic”, Mechanical Science Tech., 20(5), 634–642. |
| [9] | Robert Benjamin Gorbet, “Control of hysteresis systems with Preisach representations”, PhD thesis, University of Waterloo, Waterloo, Ontario, Canada, 1997. |
| [10] | Q. Wang, C. Su, Y. Tan, “On the Control of Plants with Hysteresis: Overview and a Prandtl-Ishlinskii Hysteresis Based Control Approach,” Acta Automatica Sinica, 2005, 31(1):92-104. |
| [11] | M. Al Janaideh, Y. Feng, S. Rakheja, C-Y Su, and C. A. Rabbath, “Hysteresis compensation for smart actuators using inverse generalized Prandtl-Ishlinskii model,” 2009 American Control Conference Hyatt Regency Riverfront, St. Louis, MO, USA, June 10-12. |
| [12] | M. Krasnoselskii and A. Pokrovskii, Systems with Hysteresis, Nauka, Moscow 1983; Springer-Verlarg Inc., 1989. |
| [13] | M. Al Janaideh, S. Rakheja, and C-Y Su, “A generalized Prandtl-Ishlinskii model for characterizing hysteresis nonli-nearities of smart actuators,” Smart Materials and Structures, 2009, vol. 18, no. 4, pp. 1-9. |
| [14] | K. Kuhnen, “Modeling, identification and compensation of complex hysteretic nonlinearities,” European Journal of Control, 2003, vol. 9, pp. 407–418. |
| [15] | D. A. Philips, L. R. Dupre, J. A. Melkebeek, “Comparison of Jiles and Preisach hysteresis models in magnetodoynamics,” IEEE Transaction Magn., MAG-31, 1995, 3551-3553. |
| [16] | Z. Bo, D. C. Lagoudas, “Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part IV: modeling of minor hysteresis loops,” International Journal of Engineering Science, 1999, vol 37:1205-1249. |
| [17] | Mittal Samir, Menq Chia-Hsiang, “Hysteresis compensation in electromagnetic actuators through Preisach model inversion”, IEEE/ASME Trans Mech, 2000;5(4):394–409. |
| [18] | Hughes D., Wen JT., “Preisach modeling of piezoceramic and shape memory alloys hysteresis”, Smart Mater Struct, 1997;3:287–300. |
| [19] | J. Koutny, M. Kruzik, A. J. Kurdila, and T. Roubicek., “Identification of Preisach-type hysteresis operators”, Nu-merical Functional Analysis and Optimization, January 2008, 29 (1). |
| [20] | H. T. Banks, A. j. Kurdila and G.Webb., “Identification of hysteretic control influence operators representing smart ac-tuators Part I: Formulation”, Mathematical Problems in En-gineering, 1997, Vol 3, pp. 287-328. |
| [21] | W. Zhang, “Modeling and control of Magnetostrictive actu-ators”, PhD thesis, University of Kentucky, Lexington, Kentucky, USA, 2005. |
| [22] | Y. F. Wang, “Methods for modeling and control of systems with hysteresis of Shape Memory Alloy actuators”, PhD thesis, Concordia University, Montreal, Quebec, Canada, 2006. |
| [23] | G. V. Webb, D. C. Lagoudas and A. J. Kurdila, “Hysteresis modeling of SMA actuators for control applications”, Journal of Intelligent Material Systems and Structures, 1998; 9; 432-448. |
| [24] | B. S. Koh, “Adaptive inverse modeling of a Shape Memory Alloy wire actuator and tracking control with the model”, M.S Thesis, Texas A&M University, College Station, TX, 2006. |
| [25] | W. S. Galinaitis, “Two methods for modeling scalar hysteresis and their use in controlling actuators with hysteresis”, PhD thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, USA, 1999. |
| [26] | F. Presiach, “Uber die magnetische nachwirkung”, Zeitscrift fur Physik, 94:277-302, 1935. |
| [27] | G. Webb, “Adaptive identification and compensation of a class of hysteresis operators,” PhD thesis, Texas A&M University, College Station, TX, May 1998. |
| [28] | M. Novotny, J. Kilpi, “Shape Memory Alloys (SMA),” [on-line]. Available on: http://www.ac.tut.fi/aci/courses/ACI-51106/pdf/SMA/SMA-introduction.pdf |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML