| [1] | L. Wang. “A new algorithm for solving classical Blasius equation”, Applied Mathematics and Computation, 157(1), 2004, 1-9. |
| [2] | I. Hashim. “Comments on ‘A new algorithm for solving classical Blasius equation’ by L. Wang”, Applied Mathematics and Computation, 176(2), 2006, 700-703. |
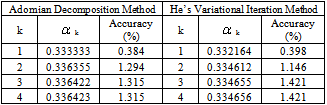
| [3] | S. Abbasbandy “A numerical solution of Blasius equation by Adomian’s decomposition method and comparison with homotopy perturbation method”, Chaos, Solitons and Fractals, 31, 2007, 257-260. |
| [4] | L. Yu, C. Chen. “The solution of the Blasius equation by differential transformation method”, Mathematical and Computer Modeling, 28(1), 1998, 101-111. |
| [5] | J. Lin. “A new approximate iteration solution of Blasius equation”, Communications in Nonlinear Science and Numerical Simulation, 4(2), 1999, 91-94. |
| [6] | B. Yao, J. Chen. “A new analytical solution branch for the Blasius equation with a shrinking sheet”, Applied Mathematics and Computation, 215(3), 2009, 1146-1153. |
| [7] | K. Parand, A. Taghavi. “Rational scaled generalized Laguerre function collocation method for solving the Blasius equation”, Journal of Computational and Applied Mathematics, 233(4), 2009, 980-989. |
| [8] | J.-H. He, “Variational iteration method – a kind of non-linear analytical technique: some examples”, International Journal of Non-Linear Mechanics, 34(4), 1999, 699-708. |
| [9] | J.-H. He, “Variational iteration method for autonomous ordinary differential systems”, Applied Mathematics and Computation, 114(2/3), 2000, 115-123. |
| [10] | J.-H. He, “Variational iteration method for delay differential equations”, Communications in Nonlinear Science and Numerical Simulation, 2(4), 1997, 235-236. |
| [11] | S.-Q. Wang, J.-H. He, “Variational iteration method for solving integro-differential equations”, Physics Letters A, 367(3), 2007, 188-191. |
| [12] | Y. Liu, C.S. Gurram, “The use of He’s variational iteration method for obtaining the free vibration of an Euler–Bernoulli beam”, Mathematical and Computer Modelling, 50(11/12), 2009, 1545-1552. |
| [13] | D. Słota. “Exact solution of the heat equation with boundary condition of the fourth kind by He’s variational iteration method”, Computers & Mathematics with Applications, 58(11/12), 2009, 2495-2503. |
| [14] | H. Taria, D.D. Ganji, H. Babazadeh. “The application of He's variational iteration method to nonlinear equations arising in heat transfer”, Physics Letters A, 363(3), 2007, 213-217. |
| [15] | D.D. Ganji, M. Jannatabadi, E. Mohseni, “Application of he’s variational iteration method to nonlinear Jaulent-Miodek equations and comparing it with ADM”, Journal of Computational and Applied Mathematics, 207(1), 2007, 35-45. |
| [16] | M. Dehghan, M. Tatari, “The use of He’s variational iteration method for solving a Fokker-Planck equation”, PhysicaScripta, 74, 2006, 310-316. |
| [17] | S. Abbasbandy, “An approximation solution of a nonlinear equation with Riemann-Liouville’s fractional derivatives by He’s variational iteration method”, Journal of Computational and Applied Mathematics, 207(1), 2007, 53-58. |
| [18] | S.M. Varedi, M.J. Hosseini, M. Rahimi, D.D. Ganji, “He’s variational iteration method for solving a semi-linear inverse parabolic equation”, Physics Letters A, 370(3/4), 2007, 275-280. |
| [19] | B. Batiha, M.S.M. Noorani, I. Hashim, E.S. Ismail, “The multistage variational iteration method for a class of nonlinear system of ODEs”, PhysicaScripta, 76(4), 2007, 388-392. |
| [20] | S.M. Goh, M.S.M. Noorani, I. Hashim, “A new application of variational iteration method for the chaotic Rossler system”, Chaos, Solitons and Fractals, 42(3), 2009, 1604-1610. |
| [21] | S.M. Goh, M.S.M. Noorani, I. Hashim, M.M. Al-Sawalha, “Variational iteration method as a reliable treatment for the hyperchaoticRossler system”, International Journal of Nonlinear Sciences and Numerical Simulation, 10(3), 2009, 363-371. |
| [22] | L. Howarth, “On the solution of the laminar boundary layer equations”, Proceedings of The Royal Society A: Mathematical, Physical & Engineering Sciences, 164, 1938, 547-579. |

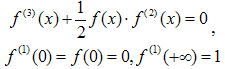

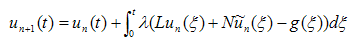
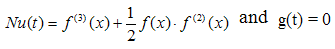
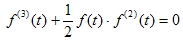
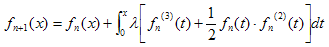
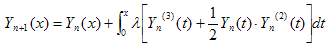
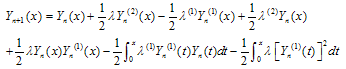
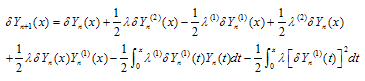
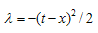
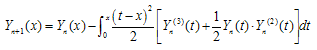
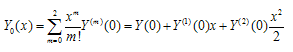
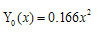
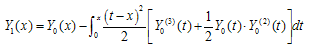
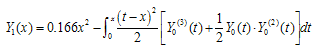
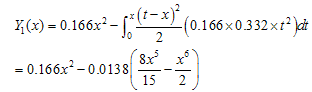
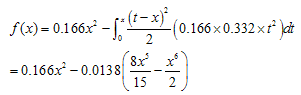
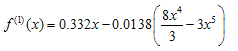
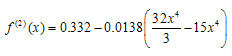
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML