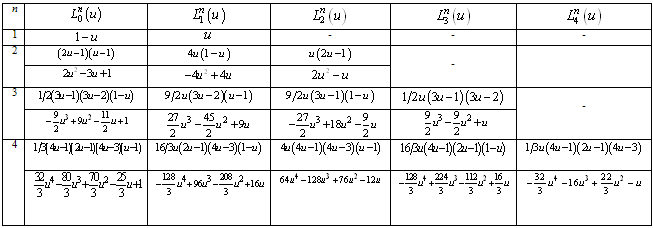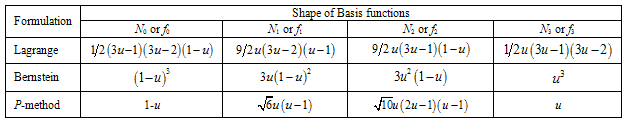-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Applied Mathematics
p-ISSN: 2163-1409 e-ISSN: 2163-1425
2011; 1(1): 13-23
doi:10.5923/j.am.20110101.02
Equivalent Finite Element Formulations for the Calculation of Eigenvalues Using Higher-Order Polynomials
C. G. Provatidis
Department of Mechanical Engineering, National Technical University of Athens, Athens, GR-157 80, Greece
Correspondence to: C. G. Provatidis , Department of Mechanical Engineering, National Technical University of Athens, Athens, GR-157 80, Greece.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
This paper investigates higher-order approximations in order to extract Sturm-Liouville eigenvalues in one-dimensional vibration problems in continuum mechanics. Several alternative global approximations of polynomial form such as Lagrange, Bernstein, Legendre as well as Chebyshev of first and second kind are discussed. In an instructive way, closed form analytical formulas are derived for the stiffness and mass matrices up to the quartic degree. A rigorous proof for the transformation of the matrices, when the basis changes, is given. Also, a theoretical explanation is provided for the fact that all the aforementioned alternative pairs of matrices lead to identical eigenvalues. The theory is sustained by one numerical example under three types of boundary conditions.
Keywords: Finite Elements, Galerkin/Ritz, Global Approximation, P-Methods, Eigenvalue Analysis
Cite this paper: C. G. Provatidis , Equivalent Finite Element Formulations for the Calculation of Eigenvalues Using Higher-Order Polynomials, Applied Mathematics, Vol. 1 No. 1, 2011, pp. 13-23. doi: 10.5923/j.am.20110101.02.
Article Outline
1. Introduction
- In the framework of the standard Galerkin/Ritz method for the solution of one-dimensional boundary value problems governed by a differential equation within the domain [0,L], the usual procedure consists of subdividing [0,L] into a certain number of finite elements for which piecewise-linear (i.e., local) interpolation is assumed[1]. In general, the shortest the elements are the more accurate the numerical solution is (h-version). Alternatively, higher order p-methods[2] suggest the introduction of nodeless basis functions based on differences of Legendre polynomials (up to the seventh degree) that cooperate with the two linear shape functions, i.e.,
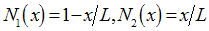 , the latter associated to the ends x = 0 and x = L. A literature survey suggests that for a certain discretization of the domain, the corresponding p-version is generally more accurate than the h-version[3-6].The matter of using higher order approximations through computer-aided-design (CAD) based Coons-Gordon macroelements has been recently discussed for two- and three-dimensional problems[7-11]. In those works some similarities and differences of the so-called ‘Coons macroelements’ with respect to the ‘higher order p-method’ have been reported in detail. Moreover, alternative CAD based NURBS or/and Bézier techniques have been proposed within the last eighteen years[12-16].In this context, this paper continues the investigation on the eigenvalue problem by moving from 2-D and 3-D to 1-D eigenvalue problems, and seeks for any similarities or essential differences between five alternative methods. The study includes classical Lagrange polynomials and extends to the Bernstein polynomials that are inherent in the definition of Bézier CAD curves[17], as well as to Chebyshev polynomials that have been previously used in spectral and collocation methods (e.g.[18]). In this paper it was found that all the aforementioned polynomials are equivalent in the sense that (after the proper transformation) they symbolically coincide with the classical higher order p-method (or p-version)[2] as well as with the class
, the latter associated to the ends x = 0 and x = L. A literature survey suggests that for a certain discretization of the domain, the corresponding p-version is generally more accurate than the h-version[3-6].The matter of using higher order approximations through computer-aided-design (CAD) based Coons-Gordon macroelements has been recently discussed for two- and three-dimensional problems[7-11]. In those works some similarities and differences of the so-called ‘Coons macroelements’ with respect to the ‘higher order p-method’ have been reported in detail. Moreover, alternative CAD based NURBS or/and Bézier techniques have been proposed within the last eighteen years[12-16].In this context, this paper continues the investigation on the eigenvalue problem by moving from 2-D and 3-D to 1-D eigenvalue problems, and seeks for any similarities or essential differences between five alternative methods. The study includes classical Lagrange polynomials and extends to the Bernstein polynomials that are inherent in the definition of Bézier CAD curves[17], as well as to Chebyshev polynomials that have been previously used in spectral and collocation methods (e.g.[18]). In this paper it was found that all the aforementioned polynomials are equivalent in the sense that (after the proper transformation) they symbolically coincide with the classical higher order p-method (or p-version)[2] as well as with the class 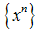 (Taylor series).
(Taylor series). 2. Galerkin/Ritz Formulation
2.1. General
- A general Sturm-Liouville problem can be written in the following differential equation
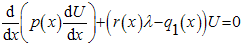 It can be reduced to a study of the canonical Liouville normal form
It can be reduced to a study of the canonical Liouville normal form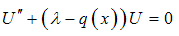 | (1) |
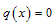 , for which Eq(1) degenerates to the well-known ‘Helmholtz equation’:
, for which Eq(1) degenerates to the well-known ‘Helmholtz equation’: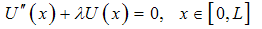 | (2) |
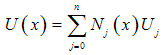 | (3a) |
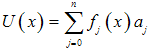 | (3b) |
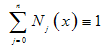 for all
for all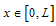 . There are also some formulations in which both shape and basis functions participate such as higher order p-methods[2]. In any case, the Galerkin/Ritz procedure[1] consists first of the Galerkin method, i.e.
. There are also some formulations in which both shape and basis functions participate such as higher order p-methods[2]. In any case, the Galerkin/Ritz procedure[1] consists first of the Galerkin method, i.e.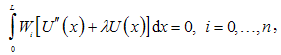 with
with 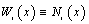 denoting the weighting function, and second by the partial integration of the second order term
denoting the weighting function, and second by the partial integration of the second order term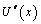 , which finally leads to the alternative matrix formulations:
, which finally leads to the alternative matrix formulations: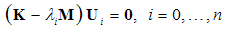 | (4a) |
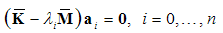 | (4b) |
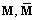 ) and stiffness (
) and stiffness (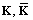 ) matrices are given by:
) matrices are given by: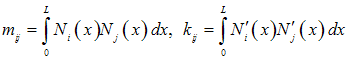 | (5a) |
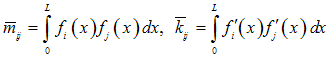 | (5b) |
2.2. Basis Functions and Shape Functions
- Below, occasionally either the Cartesian coordinate
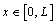 or its normalized value
or its normalized value 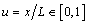 will be used. It is well known that any interval [a, b] can be reduced to[0,1] by a simple change of variable
will be used. It is well known that any interval [a, b] can be reduced to[0,1] by a simple change of variable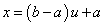 .
. 2.2.1. First Degree (Linear) Finite Element
- According to the standard literature[1], for a finite element of length lk, the two linear shape functions, that is
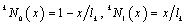 , are associated to the ends x = 0 and x = lk. It is well known[1] that the basis functions related to the aforementioned shape functions are:
, are associated to the ends x = 0 and x = lk. It is well known[1] that the basis functions related to the aforementioned shape functions are: 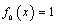 and
and , that is
, that is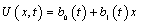 .
. 2.2.2. Lagrangian Type Macroelement
- The domain [0,L] is subdivided into n (preferably equidistant) segments, thus leading to
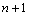 nodes. Then, the variable U is globally interpolated within the entire domain [0,L] in terms of
nodes. Then, the variable U is globally interpolated within the entire domain [0,L] in terms of 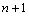 Lagrange polynomials associated to the aforementioned nodes. For a non-decreasing sequence of
Lagrange polynomials associated to the aforementioned nodes. For a non-decreasing sequence of 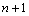 points,
points, 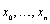 , the Lagrange polynomial
, the Lagrange polynomial 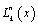 is defined as:
is defined as: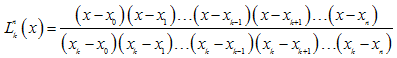 | (6) |
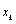 and passing through n points. Typical sets of Lagrange polynomials are shown in Table 1. Therefore, Equation (3a) holds with
and passing through n points. Typical sets of Lagrange polynomials are shown in Table 1. Therefore, Equation (3a) holds with 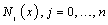 denoting the jth Lagrange polynomial (
denoting the jth Lagrange polynomial (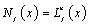 ). As for each k the denominator in Eq(6) is a constant, whereas the nominator is a polynomial of degree n, the latter can be written in terms of its roots (
). As for each k the denominator in Eq(6) is a constant, whereas the nominator is a polynomial of degree n, the latter can be written in terms of its roots (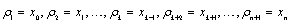 ) as follows:
) as follows:
|
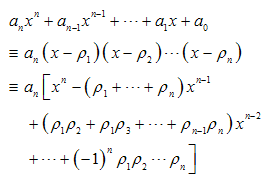
2.2.3. Bernstein Polynomials
- According to standard computer-aided-geometry knowledge, for example[17], a Bézier curve of n-th degree is defined in terms of the normalized coordinate
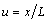 as
as 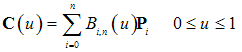 | (7) |
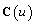 in Eq(7) is called “Bernstein polynomial of degree n” and is denoted by
in Eq(7) is called “Bernstein polynomial of degree n” and is denoted by 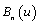 [19, p. 36], whereas the basis or blending functions,
[19, p. 36], whereas the basis or blending functions, 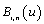 , are named “Bernstein basis” and are defined as
, are named “Bernstein basis” and are defined as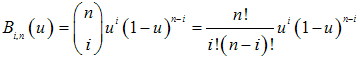 | (8) |
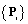 , are called control points. Equation (8) denotes that for a curve that is defined by (n + 1) control points, the highest degree is
, are called control points. Equation (8) denotes that for a curve that is defined by (n + 1) control points, the highest degree is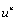 , which means that the degree of a Bézier curve is defined by the number of control points. It has been shown that Bernstein polynomials have the property of partition of unity and also the first (
, which means that the degree of a Bézier curve is defined by the number of control points. It has been shown that Bernstein polynomials have the property of partition of unity and also the first (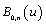 ) and the last of them (
) and the last of them (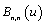 ) give unity at the first (
) give unity at the first (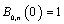 ) and the last end (
) and the last end (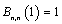 ) of the interval [0,1], respectively. It is remarkable that at any internal control point
) of the interval [0,1], respectively. It is remarkable that at any internal control point 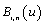 is less than the unity [17], and also vanishes at the endpoints u = 0, 1. It is trivial to prove that, at least for the case of a straight segment, when the interval [0,L] is uniformly divided into a number of so-called breakpoints, the control points coincide with them. Following the ideas of CAD/CAE integration previously proposed by the author in the context of closely related isoparametric Coons interpolation[7-11] as well as the “isogeometric” idea of Hughes et al.[14] referring to NURBS representation, in this work we propose to substitute the Cartesian coordinate
is less than the unity [17], and also vanishes at the endpoints u = 0, 1. It is trivial to prove that, at least for the case of a straight segment, when the interval [0,L] is uniformly divided into a number of so-called breakpoints, the control points coincide with them. Following the ideas of CAD/CAE integration previously proposed by the author in the context of closely related isoparametric Coons interpolation[7-11] as well as the “isogeometric” idea of Hughes et al.[14] referring to NURBS representation, in this work we propose to substitute the Cartesian coordinate 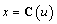 in Eq.(7) by the variable
in Eq.(7) by the variable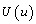 . Therefore, with respect to Eq.(3b), the basis functions
. Therefore, with respect to Eq.(3b), the basis functions 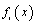 correspond to
correspond to 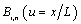 and also the control points
and also the control points 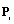 are replaced by the coefficients
are replaced by the coefficients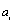 .
. 2.2.4. Higher Order P-Method
- Following Szabó and Babuška[2], the variable is expanded to a series like that in Eq(3b). According to this technique [2, p.38], the two first basis functions, which correspond to x=0 and x=L, are identical with the linear shape functions associated to the end points of the entire interval [0,L], i.e.,
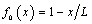 and
and 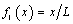 and are called nodal shape functions. The rest (n-1) basis functions are called internal shape functions and are taken as suitable integrals of Legendre polynomials properly multiplied by specific coefficients dependent on the ascending order. It must become clear that the latter refer to nodeless quantities (general coefficients) and, therefore, they are also called “bubble modes”. By elaborating on [2], in cases of n = 2, 3 and 4, the bubble basis functions are given by (
and are called nodal shape functions. The rest (n-1) basis functions are called internal shape functions and are taken as suitable integrals of Legendre polynomials properly multiplied by specific coefficients dependent on the ascending order. It must become clear that the latter refer to nodeless quantities (general coefficients) and, therefore, they are also called “bubble modes”. By elaborating on [2], in cases of n = 2, 3 and 4, the bubble basis functions are given by (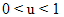 ):
):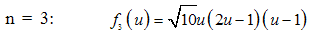 | (9b) |
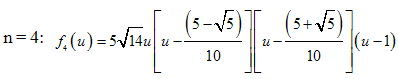 | (9c) |
2.2.5. Chebyshev Polynomials
- Chebyshev polynomials are categorized as first and second kind.I. First kind
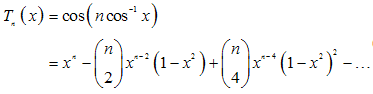 | (10a) |
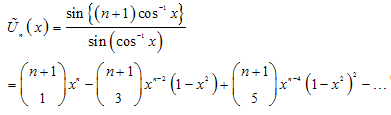 | (10b) |
2.2.6. General Remarks
- From the above analysis, it becomes obvious that Lagrange, Bernstein, Legendre, and Chebyshev polynomials are different options with the following characteristics:I. Lagrange polynomials are cardinal shape functions that operate directly on the nodal values,
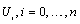 .II. Bernstein (basis) polynomials are generally non-cardinal basis functions. The only exception are the two basis functions,
.II. Bernstein (basis) polynomials are generally non-cardinal basis functions. The only exception are the two basis functions, 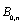 and
and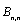 , which are associated to the ends (x = 0, x = L); thus they operate directly on the nodal boundary values
, which are associated to the ends (x = 0, x = L); thus they operate directly on the nodal boundary values 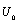 and
and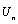 . The remaining coefficients
. The remaining coefficients 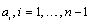 are associated to the internal control points
are associated to the internal control points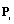 .III. Legendre polynomials create bubble basis functions
.III. Legendre polynomials create bubble basis functions 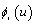 that operate on nodeless generalized coefficients, a.IV. Chebyshev polynomials (both of first and second kind) differ from the above cases in the sense that they neither become unit nor vanish at the ends of the domain. A careful inspection of all above five polynomial interpolations [Eqs.(6),(8),(9) and (10)], and considering the well known binomial expansion
that operate on nodeless generalized coefficients, a.IV. Chebyshev polynomials (both of first and second kind) differ from the above cases in the sense that they neither become unit nor vanish at the ends of the domain. A careful inspection of all above five polynomial interpolations [Eqs.(6),(8),(9) and (10)], and considering the well known binomial expansion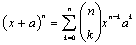 , it is easily concluded that all these polynomials can be expanded in a Taylor (power) series of the form:
, it is easily concluded that all these polynomials can be expanded in a Taylor (power) series of the form: 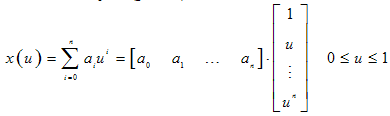 | (11) |
 [Eq(11)] are derived.
[Eq(11)] are derived. 2.2.7. Special Cases
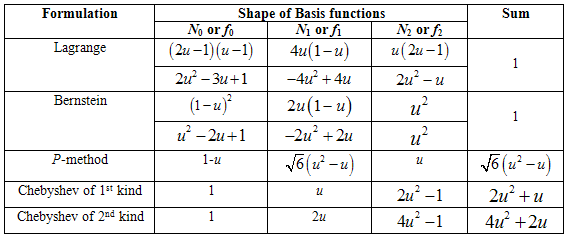
- In order to bring insight in the topic of subsection 2.2.6, some special cases of small size will be discussed in full detail. I. First, in the first four (Lagrange, Bernstein, P-method, Chebyshev of 1st kind) alternative types of polynomials, the case of using only one segment for the discretization (n = 1) is strictly related to the linear interpolation between the two endpoints. Therefore, the same classical finite element matrices, which are given below by Eq.(12a) and (12b), are obtained. For Chebyshev of 2nd kind (
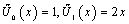 ), the factor “2” in
), the factor “2” in 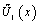 induces a slight modification. II. Second, in the case of two subdivisions, equivalent polynomials which include terms up to the second degree, is represented in Table 2. From Table 2, it becomes obvious that all functional sets are complete, as they include all the terms of the set {1, u, u2}. Moreover, while Lagrange and Bernstein (basis) polynomials ensure the partition of unity (rigid body) property, the p-method and Chebyshev polynomials do not.
induces a slight modification. II. Second, in the case of two subdivisions, equivalent polynomials which include terms up to the second degree, is represented in Table 2. From Table 2, it becomes obvious that all functional sets are complete, as they include all the terms of the set {1, u, u2}. Moreover, while Lagrange and Bernstein (basis) polynomials ensure the partition of unity (rigid body) property, the p-method and Chebyshev polynomials do not.3. Analytically Calculated Matrices
- Based on Eqs(5), the stiffness and mass matrices are analytically calculated through manipulation and are shown below.
3.1. Linear Interpolation (n = 1)
- In this case, all three formulations of this paper degenerate to the simple case of the conventional linear finite element of the literature[1]. The matrices are given by:
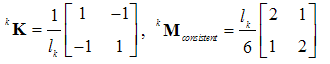 | (12) |
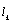 denotes the length of the finite element. It is well known that accuracy increases when the total length L of the domain is divided into an increasing number of such elements (h-version). In this case, the total mass and stiffness matrices are obtained from the assemblage of all finite elements involved [1].
denotes the length of the finite element. It is well known that accuracy increases when the total length L of the domain is divided into an increasing number of such elements (h-version). In this case, the total mass and stiffness matrices are obtained from the assemblage of all finite elements involved [1]. 3.2. Quadratic Approximation (n = 2)
- The relevant matrices are:1. Lagrange polynomials:
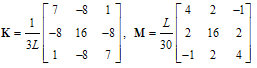 | (13a) |
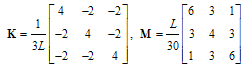 | (13b) |
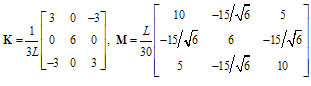 | (13c) |
3.3. Cubic Approximation (n = 3)
- Based on Eqs(5), the stiffness and mass matrices are given by:1. Lagrange polynomials:
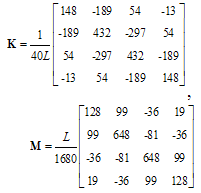 | (14a) |
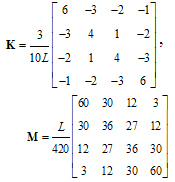 | (14b) |
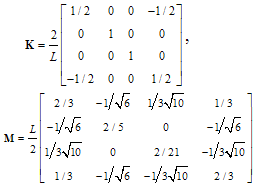 | (14c) |
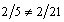 ). This fact can be explained on the basis of Table 3, where one can notice that the shape functions
). This fact can be explained on the basis of Table 3, where one can notice that the shape functions  and
and  of Lagrange and Bernstein polynomials are symmetric with respect to the central point u=1/2, while the same does not hold for the p-method.
of Lagrange and Bernstein polynomials are symmetric with respect to the central point u=1/2, while the same does not hold for the p-method. 3.4. Quartic Approximation (n = 4)
- Based on Eqs(5), the stiffness and mass matrices are given by:1. Lagrange polynomials:
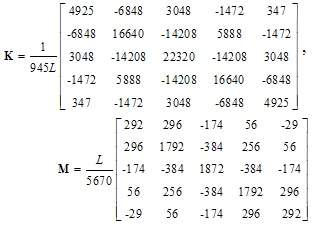 | (15a) |
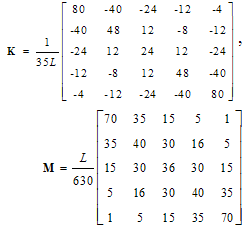 | (15b) |
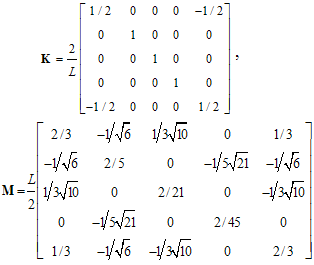 | (15c) |
 ).
).
|
|
3.5. Chebyshev Polynomial Based Matrices
- Below we present the matrices for the most general case dealt in this study, which is for the quartic approximation (
 ). Obviously, for any other m < 4, the upper left submatrix should be taken (
). Obviously, for any other m < 4, the upper left submatrix should be taken (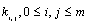 ).
).3.5.1. Chebyshev Polynomial of First Kind
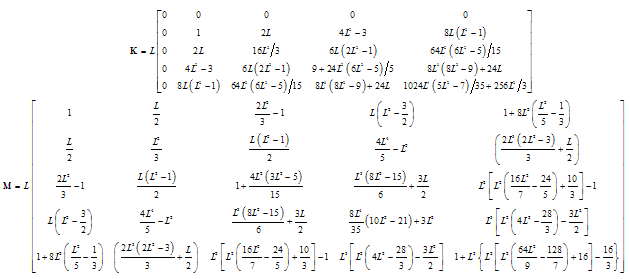 | (15d) |
3.5.2. Chebyshev Polynomial of Second Kind
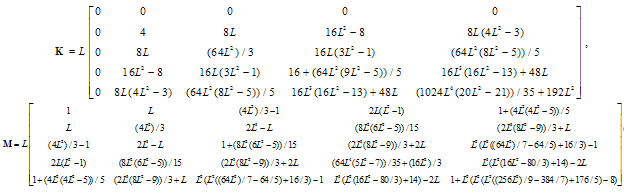 | (15e) |
3.6. Implementation of the Boundary Conditions
- In this two-point boundary value problem, three alternative types of boundary conditions may exist, as follows:i). Free-free (F-F) boundary conditions:
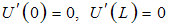 | (16a) |
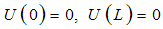 | (16b) |
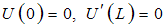 | (16c) |
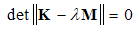 | (17) |
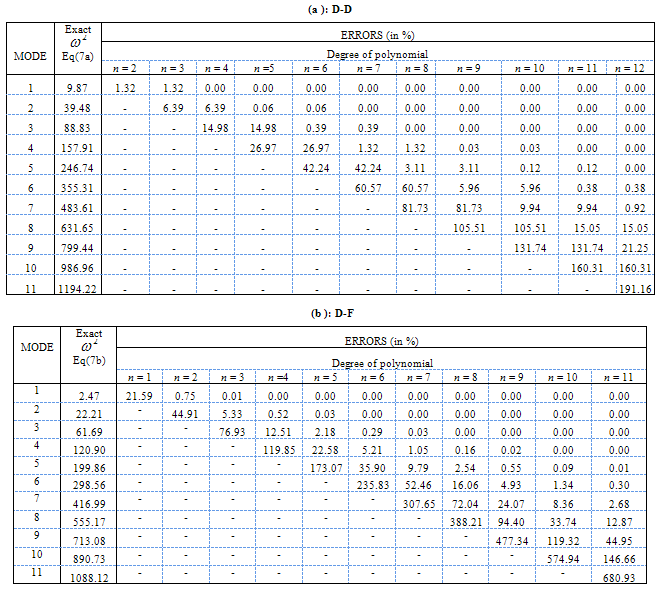
4. Numerical Results
- The domain [0, L] is subjected to either of boundary conditions (b.c.) given by Equations (16) at x = 0 and at x = L. For simplicity, the computations were performed for
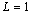 .According to the boundary conditions, the exact eigenvalues are:(i) Free-free b.c. (F-F):
.According to the boundary conditions, the exact eigenvalues are:(i) Free-free b.c. (F-F):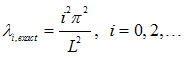 | (18a) |
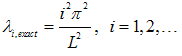 | (18b) |
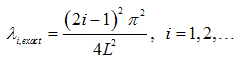 | (18c) |
 is determined as:
is determined as: 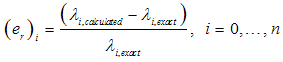 | (19) |
4.1. Free-Free (F-F) Boundary Conditions
- This case requires no special care as none row or column has to be eliminated. In all six cases, i.e. (i) Lagrange, (ii) Bernstein, (iii) p-method, (iv) Chebyshev of 1st kind, (v) Chebyshev of 2nd kind, and finally (vi) Taylor series, the eigenvalues were found to be identical. Moreover, the convergence quality is excellent (the same quality with the results presented in Table 4) but it is not presented for the sake of briefness.
4.2. One Dirichlet (D-F) or Two Dirichlet (D-D) Boundary Conditions
- For the last two types of boundary conditions [D-D and D-F: Eq(16)b,c], and for the first three types of polynomials [i.e. (i) Lagrange, (ii) Bernstein, and (iii) p-method], the row(s) and column(s) that correspond to the restricted end(s) is (are) simply eliminated. As previously happened, in all these three types of polynomials the eigenvalues were found to be identical. Moreover, convergence quality is shown in Table 4, labeled as D-D and D-F. In contrast, in case of either Chebyshev polynomials or Taylor series the way of elimination of row(s) and column(s) is not apparent yet.
5. A Theoretical Explanation
- Since all types of polynomials dealt in this study [i.e. (i) Lagrange, (ii) Bernstein, (iii) p-method and relevant Legendre polynomials, as well as (iv) Chebyshev of first and (v) Chebyshev of second kind] span the basis functions included in the class
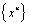 (Taylor power series):
(Taylor power series):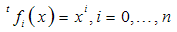 | (20) |
5.1. The Class 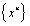
- In this case the variable U is expanded in a Taylor series:
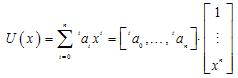 | (21) |
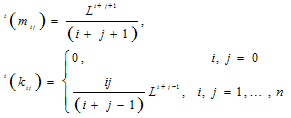 | (22) |
5.2. A Proof for the Identical Eigenvalues
- For a single square matrix
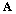 of order (n+1), Ralston and Rabinowitz[19, p. 484] (Theorem 10.3) have demonstrated that any similarity transformation
of order (n+1), Ralston and Rabinowitz[19, p. 484] (Theorem 10.3) have demonstrated that any similarity transformation 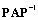 applied to
applied to 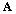 leaves the eigenvalues of the matrix unchanged. The same is found in the textbook of Bathe [20, p. 45] where, provided
leaves the eigenvalues of the matrix unchanged. The same is found in the textbook of Bathe [20, p. 45] where, provided  is orthogonal, a poof is given through the characteristic polynomial. In this paper we generalize the proof to any pair of stiffness
is orthogonal, a poof is given through the characteristic polynomial. In this paper we generalize the proof to any pair of stiffness 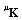 and mass
and mass 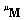 matrices (Theorem 3); the upper left superscript ‘
matrices (Theorem 3); the upper left superscript ‘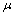 ’ takes the symbolic values ‘t’, ‘l’, ‘b’, ‘p’ as well as ‘c1’ and ‘c2’, which correspond to the initials of the six alternative polynomials (Taylor series, Lagrange polynomials, Bernstein basis, P-method/Legendre, as well as Chebyshev of 1st and 2nd kind). Theorem 1 and Theorem 2 aim to support Theorem 3.THEOREM-1. The change of basis between a basis polynomial
’ takes the symbolic values ‘t’, ‘l’, ‘b’, ‘p’ as well as ‘c1’ and ‘c2’, which correspond to the initials of the six alternative polynomials (Taylor series, Lagrange polynomials, Bernstein basis, P-method/Legendre, as well as Chebyshev of 1st and 2nd kind). Theorem 1 and Theorem 2 aim to support Theorem 3.THEOREM-1. The change of basis between a basis polynomial 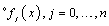 [such as Lagrange, Bernstein, P-method, Chebyshev et cetera], and the class
[such as Lagrange, Bernstein, P-method, Chebyshev et cetera], and the class 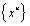 (Taylor series), induces a relationship of quadratic form between the mass matrices
(Taylor series), induces a relationship of quadratic form between the mass matrices 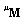 and
and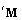 . PROOF.First, we consider the basis vectors of order (n+1), for both abovementioned functional sets:
. PROOF.First, we consider the basis vectors of order (n+1), for both abovementioned functional sets: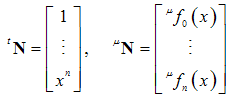 | (23) |
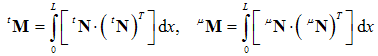 | (24) |
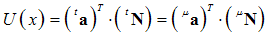 | (25) |
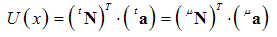 | (26) |
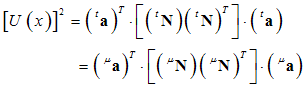 | (27) |
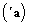 and
and 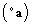 are constant (so they can exit the integral), we obtain:
are constant (so they can exit the integral), we obtain: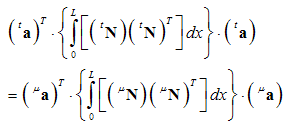 | (28) |
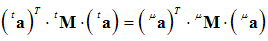 | (29) |
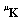 and
and 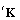 as well.PROOF.Taking the derivatives in x of the vectors in Eq(23), we obtain the two new vectors:
as well.PROOF.Taking the derivatives in x of the vectors in Eq(23), we obtain the two new vectors: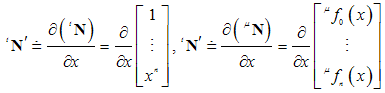 | (23a) |
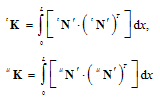 | (24a) |
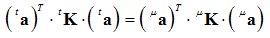 | (30) |
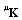 ,
,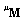 ), which corresponds to a basis polynomial
), which corresponds to a basis polynomial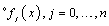 , the corresponding eigenvalues
, the corresponding eigenvalues 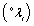 are identical with the eigenvalues
are identical with the eigenvalues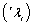 ,
, 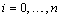 of the pair (
of the pair (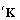 ,
,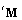 ) that is produced by the class
) that is produced by the class 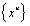 (Taylor series). PROOF.Considering the stiffness
(Taylor series). PROOF.Considering the stiffness 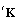 and mass
and mass 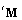 matrices [Eq(22)], the reference eigenvalue problem becomes (
matrices [Eq(22)], the reference eigenvalue problem becomes (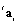 stands for the coefficients in Taylor series):
stands for the coefficients in Taylor series):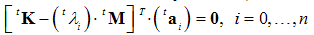 | (31) |
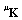 and mass
and mass 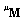 matrices, the new eigenvalue problem becomes (
matrices, the new eigenvalue problem becomes (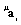 stands for the corresponding coefficients in
stands for the corresponding coefficients in 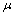 -type polynomial basis):
-type polynomial basis): 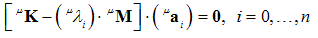 | (32) |
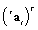 we obtain:
we obtain: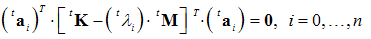 | (33) |
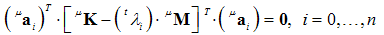 | (34) |
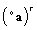 , one obtains:
, one obtains: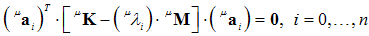 | (35) |
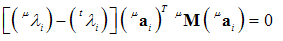 | (36) |
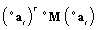 cannot vanish, it is concluded that:
cannot vanish, it is concluded that: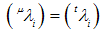 | (37) |
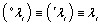 can be expressed by common Rayleigh quotients:
can be expressed by common Rayleigh quotients: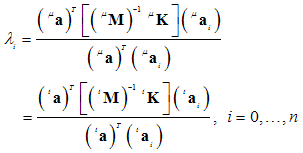 | (38) |
5.3. Application of Arbitrary Boundary Conditions
- Whatever follows is generally applicable but for the purposes of this paper it has particular value for Taylor series and Chebyshev polynomials, which do not directly apply for the boundary conditions. Equation (25) is collocated at (n + 1) points within the interval [0,L]. One possible, but not restrictive possibility is to uniformly divide the domain [0,L] into n segments, thus introducing the breakpoints:
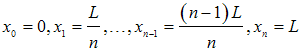 | (39) |
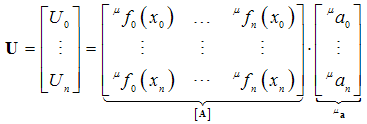 | (40) |
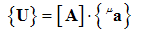 | (40a) |
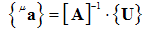 | (41) |
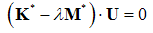 | (42) |
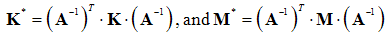 | (43) |
6. Discussion
- The motivation of this work was the interesting paper by Çelik[18] that deals with the collocation method using Chebyshev polynomials, which constitute a complete functional set. Previously, the state-of-the-art was the use of basis functions in the form of algebraic polynomials in the form
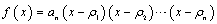 , with
, with 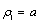 and
and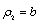 , so as to ensure satisfaction of the homogeneous Dirichlet boundary conditions in the interval [a,b] (for example, [21]). At that period the author had accumulated numerical experience on the excellent behavior of global approximation, either using B-splines or Lagrange polynomials ([7-11], among others). Later, when he tried to compare the eigenvalues obtained using (i) Lagrange polynomials, (ii) Bernstein (basis) ones, and (iii) Taylor series, a numerical coincidence was remarked when the same collocation points were used [22].The abovementioned numerical coincidence pushed the author to extend his research from collocation to the most popular finite element method in which closed form analytical formulas of the matrices can be derived. In this formulation, not only the previously found coincidence[22] was repeated, but also it was further found that the famous P-method[2] is also identical with all others. Although one could simply state that all these polynomials (Lagrange, Bernstein, Legendre, and Chebyshev) have the same basic basis, which is the class
, so as to ensure satisfaction of the homogeneous Dirichlet boundary conditions in the interval [a,b] (for example, [21]). At that period the author had accumulated numerical experience on the excellent behavior of global approximation, either using B-splines or Lagrange polynomials ([7-11], among others). Later, when he tried to compare the eigenvalues obtained using (i) Lagrange polynomials, (ii) Bernstein (basis) ones, and (iii) Taylor series, a numerical coincidence was remarked when the same collocation points were used [22].The abovementioned numerical coincidence pushed the author to extend his research from collocation to the most popular finite element method in which closed form analytical formulas of the matrices can be derived. In this formulation, not only the previously found coincidence[22] was repeated, but also it was further found that the famous P-method[2] is also identical with all others. Although one could simply state that all these polynomials (Lagrange, Bernstein, Legendre, and Chebyshev) have the same basic basis, which is the class 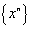 (Taylor series), the possible statement that the Rayleigh quotient is the same has to be mathematically proven. Another interesting point is the way that the boundary conditions are imposed. As previously mentioned, Lagrange polynomials are associated directly to the nodal values of the primary variable U all-over the domain, whereas the Bernstein (basis) polynomials refer to control points. However, since the extreme control points, P0 and Pn, coincide with the two ends, there is no problem to impose free-free or Dirichlet boundary conditions. Similarly, the p-method is based on the well known linear shape functions associated to the ends of the interval [a,b], and simply its functional set is enriched by the nodeless bubble functions. In contrast to the two aforementioned polynomials, similar to the Taylor series, Chebyshev polynomials have a more spectral character, as they refer to arbitrary coefficients instead of the pure values of the variable U, i.e. U0 and Un. It is worthy to mention a common characteristic similarity between Chebyshev polynomials and P-method. In more details, as the degree n of the polynomial increases, the stiffness matrix Kn and mass matix Mn (both of order (n+1)) can be immediately derived from the previously calculated submatrices Kn-1 and Mn-1 (both of order n), by simply completing the (n+1)-th row and the (n+1)-th column (it is reminded that in Section 2 the indices vary between 0,…,n).Despite the coincidence found in one-dimensional problems, preliminary comparisons in two-and three-dimensional problems suggest that there is a significant difference between Lagrangian type finite elements and the p-method, as the first occupy a broader space than the second ones [9,10].
(Taylor series), the possible statement that the Rayleigh quotient is the same has to be mathematically proven. Another interesting point is the way that the boundary conditions are imposed. As previously mentioned, Lagrange polynomials are associated directly to the nodal values of the primary variable U all-over the domain, whereas the Bernstein (basis) polynomials refer to control points. However, since the extreme control points, P0 and Pn, coincide with the two ends, there is no problem to impose free-free or Dirichlet boundary conditions. Similarly, the p-method is based on the well known linear shape functions associated to the ends of the interval [a,b], and simply its functional set is enriched by the nodeless bubble functions. In contrast to the two aforementioned polynomials, similar to the Taylor series, Chebyshev polynomials have a more spectral character, as they refer to arbitrary coefficients instead of the pure values of the variable U, i.e. U0 and Un. It is worthy to mention a common characteristic similarity between Chebyshev polynomials and P-method. In more details, as the degree n of the polynomial increases, the stiffness matrix Kn and mass matix Mn (both of order (n+1)) can be immediately derived from the previously calculated submatrices Kn-1 and Mn-1 (both of order n), by simply completing the (n+1)-th row and the (n+1)-th column (it is reminded that in Section 2 the indices vary between 0,…,n).Despite the coincidence found in one-dimensional problems, preliminary comparisons in two-and three-dimensional problems suggest that there is a significant difference between Lagrangian type finite elements and the p-method, as the first occupy a broader space than the second ones [9,10]. 7. Conclusions
- In this work, the entire one-dimensional domain [0,L] was considered as a single macroelement (global approximation), at the ends of which three (all possible) different types of boundary conditions were imposed. Also, for the spatial approximation of the variable U five different types of global higher order polynomials were considered. It was found that all these five basis functions, i.e. (i) classical Lagrange polynomials, (ii) Bernstein polynomials (useful in CAD curve representation), (iii) bubble functions based on Legendre polynomials (p-method), as well as Chebyshev polynomials of (iv) first kind and (v) second kind, share the same functional space, i.e.
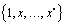 . Although the coefficients of series expansions and relevant matrices highly depend on the particular polynomial chosen, the calculated eigenvalues were found always the same, a fact that was also rigorously proven initially in case of free-free and then for arbitrary boundary conditions.
. Although the coefficients of series expansions and relevant matrices highly depend on the particular polynomial chosen, the calculated eigenvalues were found always the same, a fact that was also rigorously proven initially in case of free-free and then for arbitrary boundary conditions.
References
| [1] | Zienkiewicz, O. C., 1977, The Finite Element Method, third ed., McGraw-Hill, London |
| [2] | Szabó, B., and Babuška, I., 1991, Finite Element Analysis, John Wiley & Sons, Inc., New York |
| [3] | Szabó, B. A., and Mehta, A. K., 1978, p-convergent finite element approximations in fracture mechanics, International Journal for Numerical Methods in Engineering, 12(3), 551-560 |
| [4] | Babuška, I., Szabó, B. A. and Katz, I. N., 1981, The p-version of finite element method, SIAM Journal on Numerical Analysis, 18(3), 515-545 |
| [5] | Zienkiewicz, O. C., Gago, JPdeSR, and Kelly, D. W., 1983, The hierarchical concept in finite element analysis, Computers & Structures, 16(1-4), 53-65 |
| [6] | Friberg, O., Möller, P., Makovička, D., and Wiberg, N. E., 1987, An adaptive procedure for eigenvalue problems using the hierarchical finite element method, International Journal for Numerical Methods in Engineering, 24(2), 319-335 |
| [7] | Provatidis, C. G., 2006, Transient elastodynamic analysis of two-dimensional structures using Coons-patch macroelements, International Journal of Solids and Structures, 43(22-23), 6688-6706 |
| [8] | Provatidis, C. G., 2006, Free vibration analysis of two-dimensional structures using Coons-patch macroelements, Finite Elements in Analysis and Design, 42(6), 518 – 531 |
| [9] | Provatidis, C. G., 2006, Three-dimensional Coons macroelements: application to eigenvalue and scalar wave propagation problems, International Journal for Numerical Methods in Engineering, 65(1), 111-134 |
| [10] | Provatidis, C. G., 2006, Coons-patch macroelements in two-dimensional parabolic problems, Applied Mathematical Modelling, 30(4), 319 – 351 |
| [11] | Provatidis, C. G., 2009, Eigenanalysis of two-dimensional acoustic cavities using transfinite interpolation, Journal of Algorithms & Computational Technology, 3(4), 477 – 502 |
| [12] | Clark, B. W., and Anderson, D. C., 2003, The penalty boundary element method for combining meshes and solid models in finite element analysis, Engineering Computations, 20(4), 344-365 |
| [13] | Cottrell, J. A., Reali, A., Bazilevs, Y., and Hughes, T. J. R., 2006, Isogeometric analysis of structural vibrations, Computer Methods in Applied Mechanics and Engineering, 195(41-43), 5257-5296 |
| [14] | Hughes, T. J. R., Cottrell, J. A. and Bazilevs, Y., 2005, Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement, Computer Methods in Applied Mechanics and Engineering, 194(39-41), 4135-4195 |
| [15] | Inoue, K., Kikuchi, Y., and Masuyama, T., 2005, A NURBS finite element method for product shape design, Journal of Engineering Design, 16(2), 157-174 |
| [16] | Schramm, U., and Pilkey, W. D., 1993, The coupling of geometric descriptions and finite elements using NURBS – A study in shape optimization, Finite Elements in Analysis and Design, 15(1), 11-34 |
| [17] | Piegl, L., and Tiller, W., 1997, The NURBS Book, 2nd edition, Springer, Berlin |
| [18] | Çelik, I., 2005, Approximate calculation of eigenvalues with the method of weighted residuals-collocation method, Applied Mathematics and Computation, 160(2), 401-410 |
| [19] | Ralston, A., and Rabinowitz, P., 2001, A First Course in Numerical Analysis, Dover Publications, Mineola, New York |
| [20] | Bathe, K. J., 1982, Finite element procedures in engineering analysis, Prentice-Hall, Englewood Cliffs, New Jersey |
| [21] | Finlayson, B. A., 1972, The Method of Weighted Residuals and Variational Principles, Academic Press, New York |
| [22] | Provatidis, C. G., 2008, Free vibration analysis of elastic rods using global collocation, Archive of Applied Mechanics, 78(4), 241-250 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML