1. Introduction

Computational fluid dynamics is a branch of Engineering and science that,[1] with the help of digital computers, produces quantitative prediction of fluid-flow phenomenon based on those conservation laws governing fluid motion. These predictions normally occur under those conditions defined in terms of flow geometry. Convection- Diffusion Problems arises where fluid flow plays a significant role .We must account for the effects of convection. Diffusion occurs always alongside convection in nature. The numerical solution of convection-diffusion transport problems arises in many important applications in science and engineering. These problems occur in many applications such as in the transport of air and ground water pollutants, oil reservoir flow, in the modeling of semiconductors, and so forth[3]. This paper describes several finite difference schemes for solving the convection-diffusion equation. Therefore; we examine computation methods to predict combined convection- diffusion equation. The convection–diffusion equation is a parabolic partial differential equation combining the diffusion equation and the advection equation, which describes physical phenomena where particles or energy (or other physical quantities) are transferred inside a physical system due to two processes: diffusion and convection. In its simplest form (when the diffusion coefficient and the convection velocity are constant and there are no sources or sinks) the equation takes the form as following:

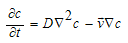The two terms on the right hand side represent different physical processes: the first corresponds to normal diffusion while the second describes convection or advection, which is why the equation is also known as the advection–diffusion equation. c is the variable of interest (species concentration for mass transfer, temperature for heat transfer), the constant D is the diffusivity for mass or heat transfer, and 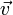is the velocity. Stationary convection-diffusion equation refers to this same equation with the time derivative omitted.

In this paper we discuss different types of Convection-Diffusion Problems and also discussed various computation methods for solving these problems. The paper is organized as follows; section two describes research work carried out by researchers for solving convection-diffusion problems in various dimensions, subsections of this section providing solution of one, two and three Diemensniol convection-diffusion problems. Linear and Nonlinear convection-diffusion problems are described in section three, in same fashion solution of steady/unsteady convection-diffusion problems are describing in section four; section five is devoted for solving singularly perturbed convection-diffusion problems. In section six we are taking convection-dominated diffusion problems and finally we are given conclusion of this article. One thing is important that the categorization given in this paper is not unique one can change this categorization; we are categorizing this paper only on the basis of a specific property of convection-diffusion problems. As for example it is possible, singularly perturbation problems can also undergoing in category of convection-dominated diffusion problems.

2. Convection-Diffusion Problems with Various Dimensions

It is discussed in introduction part of the article that the obtained governing equation of convection-diffusion problems are differential equation. In this section we are taking convection-diffusion problems of various dimensions. section 2.1 provides methods for solving the one dimensional convection-diffusion problems, similarly two Diemensniol and three Diemensniol convection-diffusion problems are discussed in section 2.2 and 2..3 respectively.

2.1. One Dimensional Convection-Diffusion Problems

In year 2010, Prashanth Nadukandi et al. Presented an article “A high-resolution Petrov–Galerkin method for the one Diemensniol convection–diffusion–reaction problem”[4]. This article was divided in seven section. Section two described high-resolution Petrov–Galerkin method (HRPG), in section three authors provided derivation of the HRPG expression via the finite-calculus (FIC) procedure, in section four authors discussing Gibbs phenomenon in L₂ -projections, in section five authors implemented the methodology to the transient convection-diffusion-reaction problem. They split the design into four model problems and derive the stabilization parameters accordingly, section six gives the Extension to multi-dimensions finally authors gives conclusion of article in section seven, which are as follow: A high-resolution Petrov–Galerkin method is presented for the one Diemensniol convection-diffusion- reaction problem. The prefix ‘high-resolution’ was used in[4] the sense popularized by Harten, i.e. second order accuracy for smooth/regular regimes and good shock- capturing in non-regular regimes. The HRPG method could be understood as the combination of upwinding plus a nonlinear discontinuity capturing operator. The distinction is that in general (multi-dimensions) the upwinding provided by h is not streamline and the discontinuity- capturing provided by 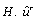is neither isotropic nor purely crosswind. The HRPG form could be considered as a particular class of the stabilized governing equations obtained via a finite-calculus (FIC) procedure. For the one Diemensniol problem, the HRPG method is similar to the CAU method with new definitions of the stabilization parameters. The one Diemensniol examples presented demonstrate that the method provides stabilized and essentially non-oscillatory i.e. monotone to-the-eye solutions for a wide range of the physical parameters and boundary conditions. It is interesting to note that the HRPG method without the linear upwinding term, i.e. using a 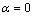does solve all the steady-state examples to give high-resolution stabilized results. Nevertheless the presence of the linear perturbation terms improves the convergence of the nonlinear iterations especially for the transient problem.

In year 2011 L.A. Sphaier proposed an article “The UNIT algorithm for solving one-dimensional convection-diffusion problems via integral transforms”[5]. A unified approach for solving convection-diffusion problems using the generalized Integral Transform Technique (GITT) was advanced and coined as the UNIT (Unified Integral Transforms) algorithm, as implied by the acronym. The unified manner through which problems are tackled in the UNIT framework allowed users that are less familiar with the GITT to employ the technique for solving a variety of partial-differential problems. This article consolidates this approach in solving general transient one-dimensional problems. Different integration alternatives for calculating coefficients arising from integral transformation are also discussed in[4]. Besides presenting the proposed algorithm, aspects related to computational implementation were also explored. Finally, benchmark results of different types of problems were calculated with a UNIT-based implementation and compared with previously obtained results. The conclusion of the article was given as; this article presented a unified algorithm for solving partial differential systems using the generalized integral transform Technique (GITT). The Unified Integral Transforms (or simply UNIT) approach, as implied by the coined acronym, was thus developed for handling a wide class of partial-differential problems in a unified way. This was accomplished by first grouping all spatial operators into a single source term. The main advantage of such approach was that a great part of the integral transformation process was carried out in one single operation. Second, this integral transformation is handled through a semi analytical integration scheme, which preserved the analytical evaluation of the oscillatory Eigen functions integrals, and provides a flexible and cost-effective alternative to automatic numerical integration routines. Finally, the mixed symbolic-numerical implementation takes the advantage of the analytical nature of the methodology.

2.2. Two Dimensional Convection-Diffusion Problems

Mariela Castillo et al.[6] described a technique for solving two-dimensional convection-diffusion equation with variable velocity with the help of Neumann series and obtain fundamental solution of two-dimensional convection –diffusion equation. The fundamental solution of the two- dimensional convection–diffusion equation with variable coefficients and its adjoint equation are obtained in complex form in terms of the unknown density of two equivalent uniquely solvable Voltera integral equations of the second kind whose analytical solutions are given explicitly as convergent Neumann series. The Volterra integral equations are obtained by integrating the complex form of the original differential equations, without additional change of variables as proposed by previously authors. In the numerical examples, cases corresponding to non-self- adjoint operators were considered. As a validation, the proposed approach is used to derive the fundamental solution of the adjoint to the convection–diffusion equation with constant velocity. In this case, the series solution can be evaluated analytically. For more general velocity fields, the recursive terms of the series can be evaluated by symbolic computation or numerical integration. In this article author tells that the boundary element method (BEM) is a very attractive solution technique, since it reduces the dimension of the problem by one unit. The basis of the BEM method is to transform the original partial differential equation (PDE) that describes a given physical problem into an equivalent integral equation, either by means of the Green’s representation formula (direct method), or by means of a continuous distribution of singular solutions of the PDE over the boundaries (indirect method). The unknowns in the integral formulation of the boundary-value problem are either the primitive variables on the boundary (direct formulation) or fictitious surface densities of the singular solutions (indirect formulation). Since the solution of the integral equation satisfies the governing field equation exactly, one seeks to satisfy the imposed boundary conditions. In this way author categorized the article in to three parts: in first, part they have given introduction of the article, in the second part, authors gave the integral-representation formulas, Riemann and fundamental solutions, in part third, fundamental solutions, as Neumann series are given after that finally, for validation of result the author have taken constant velocity.

Mehdi Dehghan[7] proposed time-splitting procedures for the Solution of the two-dimensional transport equation. The purpose of this paper is given as the diffusion-advection phenomena occurring in many physical situations such as, the transport of heat in fluids, flow through porous media, the spread of contaminants in fluids and as well as in many other branches of science and engineering. So it is essential to approximate the solution of these kinds of partial differential equations numerically in order to investigate the prediction of the mathematical models, as the exact solutions are usually unavailable. In this article, several different computational locally one-dimensional (LOD) methods were developed and discussed for solving the two-dimensional transport equation. These schemes are based on the time-splitting finite difference approximations. In section one, authors describing introduction of paper after that in section two authors describe The finite difference schemes, after that they was describing the time-splitting procedures, in section three they was describe locally one-dimensional

Technique after that LOD with the Lax-Wendroff explicit procedure. Finally, they were giving conclusion of the article: In this article, numerical methods were applied to the two-dimensional transport equation. The proposed numerical procedures solved model has been taken by author quite satisfactory. The LOD procedure is simple to implement and economical to use. It is very efficient and it needs less CPU time than the fully explicit finite difference techniques. The method of time-splitting with finite difference schemes is very easy to implement for similar three-dimensional problems, but it may be more difficult when dealing with the classical fully implicit finite difference scheme. The numerical results show a significant improvement over the traditional schemes. The LOD approach is more generally applicable than the classic approach and it represents a promising idea to derive further new algorithms which have wider stability range. One direction for future research will be to generalize the LOD procedure for higher-dimensional case. There also remain plenty of questions for future investigations: one can try to improve authors approach for developing more accurate finite difference schemes in the LOD procedure. Retention of accuracy by proper treatment on boundaries at intermediate.

2.3. Three Dimensional Convection-Diffusion Problems

In year 2010, Yongguang Chen and Bing Hu[8] proposed an article “Finite Element Programming for Three- dimensional Convection Diffusion Problems”. The classes of finite element models for convection diffusion problems are designed in C++. There are vector classes, matrix classes, element classes, material classes and method classes of finite element. On the basis of these classes, an object-oriented finite element program for three- dimensional convection diffusion problems was accomplished, which was able to simulate similar problems. It can also be applied to large universal computational software for science and engineering. In the convection- diffusion problems, when the convection effect was not apparent that Peclet number is small, finite element method for three-dimensional steady convection-diffusion equations is a high precision, stable and fast numerical methods. When Peclet number is large, the finite element mesh must be encrypted to obtain a stable solution. Traditional finite element program generally use structured methods and structured programming languages. It has some defects, such as limited expansion capability, low code reuse, and debugging complex. However, the object-oriented programming has some advantages, such as encapsulation, inheritance and polymorphism. What is more, easier debugging, maintenance, expansion, and data management security, which can greatly improve finite element software performance and the efficiency of finite element software, they will also provide favorable conditions and flexibility for integrating other software’s. As object-oriented finite element software research continues, object-oriented programming language C++ would be used. Under finite element analysis of three-dimensional convection-diffusion problems, calculation will be completed by establishing related classes.

3. Linear and Nonlinear Convection- Diffusion Problems

In year 2007 Ming Chau et al.[9] solved liner and nonlinear convection-diffusion problems by MPI implementation of parallel subdomain methods. In this article, authors discussed MPI implementation of parallel Schwarz alternating methods on distributed memory multiprocessor and also author studied parallel synchronous asynchronous iterative scheme of computation together with analysis of experimental result obtained from IBM-SP series machine. Further, authors discussed the benefits of using parallel asynchronous Schwarz alternating methods. Demonstrated that convection-diffusion problems occur very frequently in finance and hydraulics, when, Disceitizing these problems then these problems leads to very large scale systems of algebraic equation. The introduction of parallelism via decomposition techniques can be very attractive and overlapping subdomain methods, as the Schwarz alternating method, can be very efficient when they are applied to the solution of these algebraic systems of equations. The purpose of this article is to show how authors have implemented parallel overlapping subdomain methods via MPI on distributed memory multiprocessors. In particular, parallel asynchronous iterative schemes of computation are considered. In the case where several subdomains are assigned to each processor, the combination of parallel asynchronous iterative schemes of computation with the Schwarz alternating method permits one to obtain a behavior similar to the one of a multiplicative Schwarz alternating method. In first part of the article, authors have described introduction part of the article and in second part; they are discussing linear convection-diffusion problems. After that they have discussed nonlinear case taking different cases viz. nonlinearity arises on boundary or within domain and in third part of article, authors described Schwarz alternating method. The effectiveness of domain decomposition methods is well known for boundary value problems. These methods are also well suited to parallel computing. Authors concentrate here on parallel Schwarz alternating methods, which are based on overlapping sub-domains. In fourth part, they have described implementation and Asynchronous algorithms with flexible communication, Synchronous algorithms, in fifth part they have shown results and given conclusion.

In year 2008, Fuzheng Gao and Yirang Yuan[10] presente d an article for solving nonlinear Convection- dominated diffusion problem by characteristic finite volume element method. The finite volume element method (FVEM) is a discretization technique for partial differential equations, especially for those arising from physical conservation laws including mass, momentum and energy. This method has been introduced and analyzed by Li and his collaborators. The FVEM uses a volume integral formulation of the original problem and a finite element partition of the domain 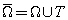to discretize the equations. The approximate solution is chosen from a finite element space. The FVEM is widely used in computational fluid mechanics and heat transfer problems. It possesses the important and crucial property of inheriting the physical conservation laws of the original problem locally. Thus it can be expected to capture shocks, to produce simple stencils, or to study other physical phenomena more effectively. The article is organized as follows: Section one, contains abstract and introduction of article: in this section authors also describing some real life problem which occur very frequently in mechanics and mathematics. CFVEM, and some important lemmas was described in section three. Section four describing convergence analysis of the problem (taken by authors). Section five describes Numerical experiment.

In year 2011, A. Shidfar et al.[11] proposed an article “Approximate analytical solutions of the nonlinear reaction-diffusion-convection problems” In this article, the series pattern solutions of the nonlinear reaction- diffusion-convection initial value problems are obtained by using the homotopy analysis method (HAM). A complete description of this method is derived and the convergence of this method is shown. Finally, two test examples are given. In this article, the homotopy analysis method was employed for solving nonlinear reaction-diffusion-convection equations with given initial conditions. The problems of these types of PDEs occur in modeling of some phenomena in sciences and engineering. The general form of recurrent relation, defined by authors in their article, for obtaining the series pattern solutions of the problems, was introduced and convergence of the method was investigated. The homotopy analysis method was a suitable method to obtain the series form approximate analytical solutions of the nonlinear problems, because it provides a convenient way to control the convergence of solution series, which was a fundamental qualitative characteristic of the HAM. In the last section, the mentioned method was applied for two test examples.

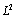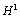In year 2011, Tong Zhang proposed[12] an article “The semidiscrete finite volume element method for nonlinear convection–diffusion problem”. In this article, a semidiscrete finite volume element method for the nonlinear convection-diffusion problem is considered. Under some regular assumptions, they obtain the and norm error estimates of numerical solution. Furthermore, they investigated two-grid finite volume element method for the considered equations. Compared with the standard method, the two-grid method is of the same order as the standard method in the 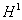-norm as long as the mesh sizes satisfy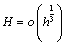. However, the two-grid method involves much less work than the standard method. Finally, some numerical results were provided to verify the established theoretical analysis. The conclusion of the article is given as: in this article, Tong Zhang considers a semidiscrete finite volume scheme for the nonlinear convection–diffusion problem. 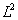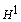The and -norm error estimates for standard finite volume method were derived under some assumptions. For two-grid algorithm, by using Taylor expression and the known solution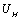, which obtained in coarse mesh, the nonlinear system transforms into a linear system, which was much easier to solve than the origin ones, numerical results confirm the effectiveness of their algorithm.

4. Steady/Unsteady Convection–Diffusion Problems

4.1. Steady State Convection–Diffusion Problems

In year 2008, A. L. Rocca1, H. Power[13] presented an article, “A double boundary collocation Hermitian approach for the solution of steady state convection-diffusion problems”. In this article a double boundary collocation approach based on the meshless radial basis function Hermitian method (symmetric method) is proposed and compared with the conventional single colloca

tion. In the double boundary collocation approach, at the boundary collocation points the boundary condition and the governing partial differential equation are required to be satisfied simultaneously instead of only the boundary condition as required in the single collocation. They were able to carry out this type of algorithm due to the robustness of the proposed Hermite interpolation scheme, in which the resulting matrix will be non-singular as long as the partial differential operators applied to each point are linearly independent; even if in a single node authors impose two different differential conditions. The results obtained with this new method are characterized by a higher precision especially for the prediction of the fluxes at the boundaries. This is due to the higher order of continuity of the approximation at the boundary points imposed by the double collocation. The main objective of authors work is to develop and test a RBF Hermitian (symmetric approach) double collocation scheme at the boundary. The scheme is similar to the one proposed by Fedoseyev et al. for the unsymmetric approach but with the difference that at each boundary collocation points the boundary condition and the governing equation are required to be satisfied simultaneously and not using different set of boundary collocation points where these conditions (boundary condition and governing equation) are independently imposed as is the case of the Fedoseyev et al. approach. The requirement of satisfying simultaneously both the boundary condition and the governing equation results in a higher order of continuity at the boundary points of the approximated solution. This article was dividing into much section: section first contains the introduction of article; Radial basis function described was in section two meshless approaches. In section three Convection-diffusion problems was describing, section four involves Numerical examples for different boundary value problems obtained obtained by double boundary collocation mesh-free method: in this section authors also discuss Convection-diffusion equation (constant velocity and variable velocity). After that author was giving conclusion of the article which are as follow: The meshless radial basis function collocation method based on the Hermite interpolation scheme is known to be a robust technique to solve convection-diffusion problems with variable coefficients. Moreover, the robustness of the Hermite scheme allows A. L. Rocca1 et al. to implement a double boundary collocation scheme, where at the boundary collocation points the boundary condition and the governing partial differential equation are required to be satisfied simultaneously instead of only the boundary condition as required in the single collocation. The proposed double boundary collocation approach results are more accurate than the single collocation on the prediction of the unknown variable. In particular it is notorious the high precision obtained on the evaluation of the boundary fluxes, which results in one order, or higher, of magnitude more accurate than the ones predicted by the single collocation approach.

In year 2009, Hoa Nguyen et al[14] proposed an article for solving Adaptive anisotropic meshing for steady convection-dominated problems. In this article authors discuss about obtaining accurate solutions for convection-diffusion equations is challenging due to the presence of layers when convection dominates the diffusion. To solve this problem, they design an adaptive meshing algorithm which optimizes the alignment of anisotropic meshes with the numerical solution. Three main ingredients are used. First, the streamline upwind Petrov-Galerkin method is used to produce a stabilized solution. Second, an adapted metric tensor is computed from the approximate solution. Third, optimized anisotropic meshes are generated from the computed metric tensor by an anisotropic centroidal voronoi tessellation algorithm. Their algorithm is tested on a variety of two-dimensional examples and the results shows that the algorithm is robust in detecting layers and efficient in avoiding non-physical oscillations in the numerical approximation. The organization of article is as follow: in section first authors describe introduction of the article, section two describe the streamline upwind Petrov-Galerkin method (SUPG) in section three authors describing Metric tensor for anisotropic mesh generation, in section four Anisotropic centroidal Voronoi tessellations (ACVT) was described, Adaptive algorithm was described in section five, section six contains Computational experiments with manufactured solutions, Computational experiments with unknown solutions was given in section six and finally they are giving concluding remarks which are as follow: author’s adaptive anisotropic mesh algorithm has substantially improved the numerical approximation for steady-state convection-diffusion problems. It works well on both diffusion-dominated and convection-dominated problems. The results converge at a quasi-optimal or optimal rate (depending on the characteristics of the layers) and with low computational cost. Due to the efficiency and robustness of authors’ algorithm, non-physical oscillations in the numerical solutions in the layers are not present. Since adaptive anisotropic meshes are used in their algorithm, any local phenomena in the solutions (for example, layers, singularities, etc.) are captured automatically. This capability will allow author’s to explore more practical and complicated problems in future.

In year 2010, Flavius Guia presented an article[15] “Direct simulation of the infinitesimal dynamics of semi-discrete approximations for convection-diffusion- reaction problems”. In this article, a scheme for approximating solutions of convection-diffusion reaction equations by Markov jump processes was studied. The general principle of the method of lines reduces evolution partial differential equations to semi-discrete approximations consisting of systems of ordinary differential equations. F. Guia approach was to use for this resulting system a stochastic scheme which is essentially a direct simulation of the corresponding infinitesimal dynamics. This implies automatically the time adaptivity and, in one space dimension, stable approximations of diffusion operators on non-uniform grids and the possibility of using moving cells for the transport part, all within the framework of an explicit method. Flavius Guia present several results in one space dimension including free boundary problems, but the general algorithm was simple, flexible and on uniform grids it can be formulated for general evolution partial differential equations in arbitrary space dimensions. This article is organized as follows: The general algorithm for approximating systems of ordinary differential equations by Markov jump processes was described in section two. Section three is dedicated to a model problem. In Section four Flavius Guia consider reaction-diffusion problems which are standard examples for employing deterministic schemes with grid adapativity in time and space. In their examples the time adapativity is given intrinsically by the stochastic method and the grid was considered to be uniform. In Section five F. Guia simulate diffusion on non-uniform grids by the same basic principle of an explicit stochastic scheme, a fact that is fairly impossible in explicit deterministic methods. This feature opens the possibility of using moving grids. In Section six they consider cells which are transported according to the corresponding velocity and diffusion is simulated on a non-uniform grid configuration. Flavius Guia apply this method to the viscous Burgers’ equation. Section 7 deals with an example of a free boundary problem, namely the Black-Scholes equation for American put options. Finally Flavius Guia given concluding remarks concerning the features of the approach, presented in this article[15].

In year 2011, N. Ahmed et al.[16] proposed an article “Discontinuous Galerkin time stepping with local projection stabilization for transient convection-diffusion-reaction problems”. A time-dependent convection-diffusion- reactions problem was discretize in space by a continuous finite element method with local projection stabilization and in time by a discontinuous Galerkin method. Authors presented error estimates for the semidiscrete problem after discretizing in space only and for the fully discrete problem. Numerical tests confirm the theoretical results. The article was organized as follows: Section two introduces the problem under consideration and defines the basic notations. The semidiscretization in space and the local projection stabilization are introduced in section three. Furthermore, an optimal error estimate for the semidiscretized problems will be given. Error analysis for the fully discrete problem after a time discretisation by a discontinuous Galerkin method was described in section four. Numerical results which confirm the theoretical predictions Described in Section five. Finally, Section six provides some concluding remarks. They have analyzed the error estimate for the time dependent convection diffusion-reaction problem with local projection stabilization in space and discontinuous Galerkin method in time. The optimal error estimates in strong and weak norms have been obtained. From the numerical results, N. Ahmed et al. find that the parameters of LPS leads to different influences to first and second order schemes. The first order schemes are more sensitive for the parameters of LPS than the second order schemes.

4.2. Unsteady Convection–Diffusion Problems

In year 2009, Xin Cai et al.[17] proposed Finite Volume Method for time-dependent convection diffusion large Reynolds number problem. Time-dependent convection diffusion equation, with a discontinuous data and large Reynolds number, was examined. This kind of problem leads to interior layer phenomena due to the discontinuity. The solution was changes rapidly near interior layer. Traditional finite volume method is applied. Two efficient numerical methods are constructed. One is Shishkin’s finite volume method, another is Improved-Shishkin’s finite volume method. Shishkin’s finite volume method applies Shishkin’s idea to construct mesh partition. Improved- Shishkin’s finite volume method applies multitransition point’s technique to reconstruct mesh partition near interior layer. Numerical experiments indicate that both methods are well fitted the property of interior layer. Both methods are uniformly convergence scheme. Improved- Shishkin’s finite volume method was more accurate than finite difference method, which is constructed by Farrell in his previous work.

In year 2010 Jiansong Zhang and Danping Yang was presented an article[18]. “Time-dependent convection- diffusion system by Parallel least-squares finite element method”. A short description of article are given On the basis of overlapping domain decomposition, they construct a parallel least-square finite element algorithm (PLS) for solving the first-order time-dependent convection-diffusion system. The algorithm is fully parallel. At each time step, only one or two iterations are needed to reach to given accuracy. Some numerical results are supported to the theoretical results. The outline of this article[18], is as followed: The least-squares finite element procedure for the convection-diffusion system and formulation of the parallel least-squares finite element algorithm was described in section two, in Section three J. Zhang et al. Give some lemmas, which was important to prove the convergence theorem of the approximate solution. And then, authors prove convergence theorem in Section four. After that, some numerical examples are provided to confirm J. Zhang et al theoretical results in Section five. Finally, some concluding remarks are given in Section six. In this article, they have proposed a parallel least-squares finite element method for time-dependent convection-diffusion system. The advantage of this method is that only one or two iterations are needed to reach given accuracy at each time level. However, for a general iterative-type parallel algorithm, many iteration steps are needed to reach given accuracy, which produce much more global amount of computational works. Moreover, the theoretical analysis also indicates that the convergence of the PLS algorithm is independent of the number of sub-domains N. Though one dimensional convection-diffusion problem is chosen as J. Zhang et al: model in this article, in fact, this method was also applied for more general problems and multidimensional problems, e.g., the Navier–Stokes equations, miscible displacement problems in porous media etc., which was author’s further work.

5. Singularly Perturbed Convection– Diffusion Problems

In year 2008, Mohan K. Kadalbajoo et al.[19] presented an article B-Spline collocation method for a two- parameter singularly perturbed convection-diffusion boundary value problems. In this article they are using B-spline collocation method on piecewise-uniform Shishkin mesh, which leads to a tridiagonal linear system. The convergence analysis was also given and the method is shown to have uniform convergence of second order. Numerical results are presented in the end of the article which also supports the theoretical results. This article is divided in to six sections introductory part of the article is discussed in section first, which is given in short above, Section two involves Mesh selection strategy, in this section they formed the piecewise-uniform grid in such a way that more points are generated in the boundary layer regions than outside of it. They divide the interval[0, 1] in to three sub-interval. Section three involves B-Spline collocation method. Derivation for uniform convergence was given in section four. In section five they give numerical results and verifying with experimental convergence. In section six, they give conclusion which is as follow: B-spline collocation method for the solution of two-parameter singularly perturbed convection-diffusion boundary value problems given in[19]. It is relatively simple to collocate the solution at the mesh points, to set up the collocation system and to solve them. The results obtained using this method are more accurate then the stated existing method with same numbers of nodal points and gives the order of convergence to be two. Also this method produces a spline function which is useful to obtain the solution at any point of the interval, whereas the finite difference method gives the solution only at selected nodal points. The numerical results given in tables of article show that the present method approximates the exact solution very well.

In year 2009 G. I. Shishkin and L. P. Shishkina[20] presented an article, “higher order Richardson scheme for a singularly perturbed Semilinear Elliptic Convection– Diffusion Equation” .The Dirichlet problem on a vertical strip is examined for a singularly perturbed semi linear elliptic convection–diffusion equation. For this problem, the basic nonlinear difference scheme based on the classical approximations on piecewise uniform grids condensing in the vicinity of boundary layers converges 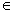-uniformly with an order at most almost one. The Richardson technique is used to construct a nonlinear scheme that converges 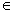-uniformly with an improved order, namely, at the rat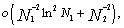e where 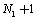and 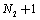are the number of grid nodes along the 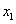-axis and per unit interval of the 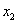-axis, respectively. This nonlinear basic scheme underlies the linearized iterative scheme, in which the nonlinear term is calculated using the values of the sought function found at the preceding iteration step. The latter scheme was used to construct a lineralized iterative Richardson scheme converging 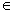-uniformly with an improved order. Both the basic and improved iterative schemes converge 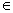-uniformly at the rate of a geometric progression as the number of iteration steps grows. The upper and lower solutions to the iterative Richardson schemes are used as indicators, which makes it possible to determine the iteration step at which the same 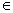-uniform accuracy is attained as that of the non-iterative nonlinear Richardson scheme. It was shown that no Richardson schemes exist for the convection-diffusion boundary value problem converging 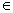-uniformly with an order greater than two. Principles were discussed on which the construction of schemes of order greater than two can be based. This article is divided in to various part: in first part, authors are given introduction of problem which are arising in real life system, after that they are giving statement of the problem. In next section they, describe the priori bounds on solutions and their derivatives, finally authors are giving conclusion. In this article[20], Richardson schemes of improved accuracy were constructed for the boundary value problem on a vertical strip for the singularly perturbed semilinear elliptic Convection-Diffusion equation. These schemes converge-uniformly in the maximum norm with the second order (up to a logarithmic factor).

In year 2009 Katarina Surla et al.[21] proposed an article “A robust layer-resolving spline collocation method for a Convection-Diffusion problem”. They consider finite difference approximation of a singularly perturbed one-dimensional convection-diffusion two-point boundary value problem. The problem is numerically treated by a quadratic spline collocation method on a piecewise uniform slightly modified Shishkin mesh. The position of collocation points is chosen so that the obtained scheme satisfies the discrete minimum principle. They prove pointwise convergence of order 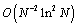inside the boundary layer and second order convergence elsewhere. The uniform convergence of the approximate continual solution is also given. Further, they approximate normalized flux and give estimates of the error at the mesh points and between them. The numerical experiments presented in the article confirm their theoretical results. The paper is organized as follows: In Section two, K. Surla et al. recall the decomposition of the problem taken in article[21] and its properties and give the construction of Shishkin mesh and derivation of the spline difference scheme. Section three is devoted to the construction of the barrier function for the boundary layer function. In Section four, pointwise convergence of the method and uniform pointwise convergence of the normalized flux was proved in section four and five, while Section six contains the proof of uniform convergence of the normalized flux between the mesh points on a slightly modified Shishkin mesh. In Section seven, Katarina Surla et al. give the convergence result for the continual solution. Finally, the numerical results were presented in Section eight.

In year 2011, Peng Zhu et al.[22] presented an article “A uniformly convergent continuous-discontinuous Galerkin method for singularly perturbed problems of convection-diffusion type”. In this article, they introduce a coupled approach of local discontinuous Galerkin and standard finite element method for solving singularly perturbed convection–diffusion problems. On Shishkin mesh with linear elements, a rate 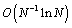in an associated norm is established, where N is the number of elements. Numerical experiments complement the theoretical results. Moreover, a rate 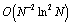in a discrete 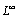norm, and 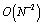in 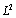norm, are observed numerically on the Shishkin mesh. The article is organized as follows: the coupled LDG and CFEM for the singularly perturbed problems were introduced in section two. The stability and error analysis of the coupled method with linear elements on a Shishkin mesh is given in Section three. The implementation of their coupled method on a Shishkin mesh is presented in Section four. The aims of article to validate author’s theoretical result. Further, they numerically observe the uniform convergence rate 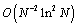in a discrete 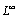norm, and 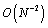in 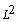norm. Finally in last Section five authors give some concluding remarks. In the sequel, with C Peng Zhu et al. would denote a generic positive constant independent of the perturbation parameter 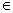and mesh size.

In year 2011, Fatih Celiker et al.[23] present an article “Nodal Super convergence of SDFEM for Singularly Perturbed Problems”. In this article, they analyzed the streamline diffusion finite element method for one dimensional singularly perturbed Convection-Diffusion- reaction problems. Local error estimates on a sub-domain where the solution was smooth are established. The organization of the article is as follows: In Section two, they display the method and state their main results in[23]. The proof of these results was given in Section three. Numerical results verifying the sharpness of author’s. Theoretical findings are provided in Section four. At last authors gave his concluding remark which is as follows: authors considered streamline diffusion finite element method (SDFEM) for one dimensional singularly-perturbed convection-diffusion reaction problems. They proved that on Shishkin-type meshes the nodal error super converges with a rate of order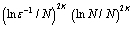, depending on the choice of the transition point of the mesh. Their result can be considered as an extension to the singularly-perturbed regime of the nodal estimate proved by Douglas and Dupont in[23]. Celiker and Cockburn[23] proved a super convergence result similar to that of Douglas and Dupont for the discontinuous Galerkin method. However, their result is the first such result for singularly-perturbed problems. In a forth coming article, they will consider an element-by-element post processing resulting in a new approximation that converges with the same rate as that of the nodal error throughout the computational domain. The other part of their main result is a local error estimate. They prove that, in a suitably defined norm, the error of the SDFEM converges uniformly in 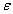in the part of the mesh where the exact solution is regular. In other words, they prove uniform-in- 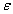convergence away from the boundary layer.

6. Convection-Dominated Diffusion Problems

In the year 2007, Petr Knobloch “Numerical Solution of Convection–Diffusion Equations Using a Nonlinear Method of Upwind Type”[24] presented an article. The focus of the author was on scalar Convection-Diffusion problem which is solved by using a nonlinear method of upwind type. In this article the author extended Mizukami-Hughes method which is a nonlinear method of upwind type using conforming piecewise linear triangular finite elements. The author extended this method on whole range of the diffusion parameter whereas the original method was introduced for the convection-dominated regime only. After that the author proved that the extended method satisfies the discrete maximum principle and also illustrated its properties by means of numerical results. This article categorized in to six parts: the first parts contain introduction of the article, second part contains streamline upwind/Petrov–Galerkin method (SUPG) Method and spurious oscillations at layers diminishing methods (SOLD), third part contains Mizukami–Hughes Method, in fourth part the author describes the improved Mizukami–Hughes method in fifth part the author describes suppression of the Upwind Character of the Mizukami–Hughes Method. In introduction part, the author give a discussion about some numerical techniques.

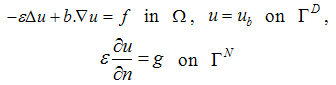(1)

Since it is well known that the numerical solution of (1) is a challenging task since convection often dominates diffusion and hence the solution of (1) typically contains narrow inner and Boundary layers. Discrete solutions of (1) are then often polluted by spurious oscillations. Therefore, many various stabilized methods have been developed during the past decades. At last author has given conclusion of this article, which is the improved Mizukami-Hughes method applied to scalar steady Convection-Diffusion equations in small and moderate Peclet number regimes. Author has shown that, in this case, the method introduces two much artificial diffusion, which may decrease the accuracy of the discrete solution. Therefore, they proposed modifications of the Mizukami–Hughes method, which preserve its favorable properties for large Peclet numbers and reduce its upwind character if the Peclet number is small. Numerical Results justify the proposed modifications.

In year 2007 Volker John et al.[25] proposed an article on spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations. In this article, authors proposed that “in streamline upwind/Petrov- Galerkin (SUPG) stabilization of convection-dominated convection-diffusion equations is the presence of spurious oscillations at layers”. Since the mid of the 1980s, different methods have been proposed to remove or, at least, to diminish these oscillations without leading to excessive smearing of the layers. This article gives a review, state of the art of these methods, discussed their derivation, proposed some alternative choices of parameters in the methods and categorizes these methods. Some numerical studies which supplement this review provide a first insight into the advantages and drawbacks of the methods. In this problem[25] taken by authors is scalar Convection- Diffusion equation when convection is strongly dominant. Then basic difficulty is that, in this case, the solution of taken problem is typically possesses interior and boundary layers, which are small sub regions where the derivatives of the solution are very large. The widths of these layers are usually significantly smaller than the mesh size; due to that reason the layers cannot be resolved properly. This leads to unwanted spurious (nonphysical) oscillations in the numerical solutions, the attenuation of which has been the subject of extensive research for more than three decades. This article[25] is categorized in seven: part summary of first part are given above, in second part authors described usual Galerkin Discretisation, part three and this section also described introductory concept of SUPG method. Section four described the accuracy of the SUPG method is greatly influenced by the choice of the stabilizing parameter, section five described brief review of SOLD method. A basic problem of all SOLD methods is to find the proper amount of artificial diffusion which leads to sufficiently small nonphysical oscillations (requiring that the artificial diffusion is not ‘too small’) and to a sufficiently high accuracy (requiring that the artificial diffusion is not ‘too large’). Since the artificial diffusion is the sum of the contributions coming from the SUPG term and the SOLD term, the definition of both terms will be thoroughly presented and discussed in this article[25]. Results of numerical tests with the SOLD Methods at two typical examples are reported in section six, and finally author’s given conclusions and an outlook of article[25].

In the year 2008, Volker John et al.[26] described numerical studies of stabilized FEM for solving scalar time-dependent Convection-Diffusion-reaction equation; this article was focused on those types of problems in which diffusion was small. In their study[26], they include streamline-upwind Petrov-Glerkin (SUPG) method with different parameters, various suspicious oscillation at layers diminishing (SOLD) method. A local projection stabilization (LPS) scheme based on enrichment and two finite elements method flux corrected transport (FEM-FCT) method and then main focus was on the evaluation of the numerical results on the reduction of spurious oscillation. The basic idea in application of stabilized FEM is that after the temporal Discretisation of the time-dependent equation, the equation has the form of a steady-state Convection- Diffusion-Reaction equation. Article[26] was divided in eight sections, whose short discussion is given bellow. In section first author described the simulation of time-dependent Convection-Diffusion-Reaction equation by an example of chemical reaction and gave the introduction and various methods used in[26]. Section two contains basic discretisation and described that in the case of dominant convection the Galerkin finite element formulation becomes instable. SUPG method was described in section three. The stability of the SUPG method applied to time dependent Convection-Diffusion equation was studied analytically in[4].It can be proved that the coupling of the SUPG method to implicit time stepping schemes leads to a stable Discretisation, regardless of the length of the time step. In addition, it was pointed out that spurious oscillation may be expected for small time steps, which can be observed in numerical studies in section seven. In section four the author described (SOLD) methods; this method was used to remove spurious oscillation at layers from SUPG finite element solution of steady-state scalar convection-diffusion-reaction equation, and given merits and demerits of SOLD methods. After that author described isotropic SOLD methods. In section five the author described local projection stabilization schemes; the goal of these schemes consists in adding appropriate stabilization to small scales of the finite element solution only this approach is related to the idea of variation multiscale methods for the simulation of multiscale phenomenon .In section six the author describes the Finite element method-flux corrected transport schemes, a non-linear FEM-FCT scheme and A linear FEM-FCT .In section seven the author describes the numerical study of these methods described and after that they are considering these methods on Standard benchmark problems for time-dependent scalar Convection-Diffusion-Reaction and also discussing a body rotation problem .In section eight, Volker John et al. discussed summary of this article and found that FEM-FCT schemes were clearly the best schemes by taking an example the author shown that these scheme may lead to some spurious oscillation. In particular, the linear FEM- FCT scheme shows a very good ratio of accuracy and efficiency. The smearing which is introduced by these schemes will be tolerable in many applications. This scheme has been identified to be a promising candidate to be used in the simulation of the chemical reaction in precipitation process.

In year 2008 R. Bermejo and, J. Carpio[27] described “An adaptive finite element semi-Lagrangian implicit– explicit Runge-Kutta-Chebyshev method for convection dominated reaction–diffusion problems”. Authors introduce an adaptive method that combines semi-Lagrangian schemes with a second order implicit-explicit Runge-Kutta- Chebyshev (IMEX RKC) method to calculate the numerical solution of convection dominated reaction–diffusion problems in which the reaction terms are highly stiff. The convection terms are integrated via the semi-Lagrangian scheme, whereas the implicit-explicit Runge-Kutta- Chebyshev treats the diffusion terms explicitly and the highly stiff reaction terms implicitly. The space adaptation is done in the framework of finite elements and the criterion for adaptation is derived from the information supplied by the Semi-Lagrangian step; so that, this can be considered a heuristic approach to adapativity that is somewhat similar to the so-called r-adapativity strategy. In this article, problems taken by authors are time dependent advection-diffusion- reaction equations with highly stiff reaction terms. In second part, authors describe briefly the finite element Semi- Lagrangian implicit-explicit Runge-Kutta-Chebyshev method and this section also involves many subcategory which are Finite element Discretisation, The semi- Lagrangian IMEX RKC method after that they are surmising Semi- Lagrangian-IMEX RKC Algorithm, The adaptive method was described in section three, at every time step authors will adapt first the spatial mesh and then the length of the time step. Authors approach to mesh adaptation will be heuristic rather than analytical. Based on the goal of mesh adaptation that consists of generating a mesh adapted to the problem such that the numerical solution satisfies an error criterion, one refines the mesh in those regions where the numerical solution experiences large spatial variations, because it is in these regions where the local errors are presumably larger. On the other hand, in convection-dominated diffusion problems numerical experiments indicate that the residual of the underlying differential equation is dominated by the hyperbolic part of the equation due to the fact that important features of the solution, such as jumps and regions of strong gradients, are transported along the trajectories. Therefore, the information given by the semi- Lagrangian step of authors’ method[27] may be very valuable to devise an economical error indicator to adapt the mesh adaptive method in section four authors giving Numerical tests.

In year 2009, Pengtao Sun et al.[28], presented an article “Numerical Studies of Adaptive Finite Element Methods for Two Dimensional Convection-Dominated Problems”. In this article, authors study the stability and accuracy of adaptive finite element methods for the convection-diffusion-reaction problem (convection- dominated) in the two dimensional space. Through various numerical examples on a type of layer-adapted grids (Shishkin grids), they show that the mesh adaptivity driven by accuracy alone could not stabilize the scheme in all cases. Furthermore the numerical approximation was sensitive to the symmetry of the grid in the region where the solution was smooth. On the basis of these two observations, they develop a multilevel-homotopic-adaptive finite element method (MHAFEM) by combining streamline diffusion finite element method, anisotropic mesh adaptation, and the homotopy of the diffusion coefficient. Pengtao Sun et al. used numerical experiments to demonstrate that MHAFEM can efficiently capture boundary or interior layers and produced accurate solutions. the conclusion of article is given bellow. By performing numerical tests of the standard finite element method for convection-dominated convection-diffusion- reaction problem on different layer-adapted grids, authors demonstrated that the stabilization of a standard scheme is necessary even for the layer adapted Shishkin grids. In particular, they shown that the convergence rate is first order instead of second order in maximum norm for piecewise linear finite element when the grid was only quasi-uniform in the smooth part. They demonstrated that the streamline diffusion finite element method (SDFEM) on correctly adapted grids can produce both stable and accurate approximation. For the case of solution bearing regular boundary layers, they showen that Shishkin grid can increase the stability and accuracy of the standard finite element method. Whereas, for solutions with parabolic boundary layer only, the standard finite element method is unstable on Shishkin grid when the number of grid points in convection direction was odd. The stabilization and accuracy of a standard scheme are recovered by having even number of grid points or having a grid size being ε along the convection direction. On the other hand, by perturbing Shishkin grid points outside or inside the boundary layer, they indicate that the accuracy depends crucially on the uniformity of the grid in smooth region. Generally the convergence rate is first order instead of second order in maximum norm for piecewise linear finite element when the grid is only quasi-uniform in the smooth part. For constructing a correctly adapted grid in a posteriori manner, they presented a multilevel homotopic-adaptive finite element method (MHAFEM) based on anisotropic mesh adaptation. Numerical experiments showed that MHAFEM significantly reduces the number of degree of freedom and increase the accuracy in the process of achieving the desired ε. Mean while, the singular boundary or interior layers are accurately captured and resolved by the properly adapted grids. They note that in their approach the anisotropic meshes generated in a posteriori manner is not as good as the Shishkin grid when a priori information, e.g., the location of the layer and the width of the layer, was known. Several mesh improvement techniques will fail when ε is as small as. They could improve the robustness of the anisotropic mesh adaptation by other techniques, e.g., notably moving mesh methods. They did not address the issue of the efficiency, especially the efficient solver for the linear algebraic system. Multigrid type solvers will be deserved for further studying. Another important ingredient is the recovery of the Hessian matrix of the solution. The accuracy of recovered derivatives of u will significantly affect the mesh adaptation. They should test and report more robust recovery schemes in a future work.

In year 2009, Ningning Yan and Zhaojie Zhou[29] published an article which is “A RT Mixed FEM/DG Scheme for Optimal Control Governed by Convection-Diffusion Equations”. In this article authors provided a numerical scheme-RT mixed FEM/DG scheme for the constrained optimal control problem governed by convection dominated diffusion equations. A priori and a posteriori error estimates are obtained for the state, the co-state and the control. The adaptive mesh refinement can be applied indicated by a posteriori error estimator provided in this article. Numerical examples are presented to illustrate the theoretical analysis. In this article authors use a combined method of the Raviart-Thomas (RT) mixed FEM and the discontinuous Galerkin method (DG) to approximate the convection diffusion equation in the optimal control problem. A priori and a posteriori error estimates are obtained for both the state, the co-state and the control. The adaptive mesh refinement can be applied driven by a posteriori error estimator provided in this article[29]. This Article is organized as follows: in Section two, Authors introduce the model problem for the optimal control problem governed by convection dominated diffusion equations and present a RT mixed FEM/DG scheme as the approximation scheme of the model problem. In Section three Authors proved a priori error estimate for the new scheme on the optimal control problem. Furthermore, a posterior error estimate is established in Section four. Finally three numerical examples were presented in Section five to illustrate authors theoretical results. Finally authors gave a very important discussion of the articles which are as follow: In this article, authors’ derived a priori and a posteriori error estimates of a RT mixed FEM/DG scheme for the constrained optimal control problem governed by convection dominated diffusion equations. Numerical examples was presented to illustrate[29] theoretical results. In Their work, they pay more attention on the a priori and a posteriori error estimates of the control u, the state y and the costate z, because they are important quantities in practical control problems. 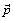More careful analysis for the auxiliary variablesand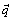is ignored, although some better results may be expected. In this area, there are many important issues that still need to be addressed. For example, authors was going to study LDG method for the optimal control problem, and try make the comparison between the LDG and the combined method of RT mixed FEM and DG in further coming work. Moreover, many computational issues have to be addressed; it was also important and challenging to investigate the optimal control problem governed by convection dominated diffusion equation of evolution.

Pedro Galan del Sastre and Rodolfo Bermej[30] published an article in 2010, which is “Error Analysis for hp-FEM Semi-Lagrangian Second Order BDF Method for Convection-Dominated Diffusion Problems”. Pedro G. d. Sastre et al. presented in this article an analysis of a Semi-Lagrangian second order backward difference Formula combined with hp-finite element method to calculate the numerical solution of convection diffusion equations in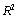. Using mesh dependent norms, authors also prove that the a priori error estimate has two components: one corresponds to the approximation of the exact solution along the characteristic curves, which is 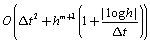; and the second, which is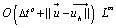, Repn resents the error committed in the calculation of the characteristic curves. Here, m is the degree of the polynomials in the finite element space, 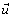is the velocity vector, 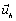is the finite element approximation of 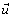and p denotes the order of the method employed to calculate the characteristics curves. Numerical examples support the validity of Pedro G. d. Sastre et al. estimates. The organization of the article is as follows: Preliminary results concerning the approximation properties of the finite dimensional spaces was presented in section two, where one seeks to approximate the solution, and they introduce the semi-Lagrangian method. The analysis of the approximation to X(x, s; t) was undertaken in Section three. Section four was devoted to the error analysis of the semi-Lagrangian Euler and second order BDF schemes. Numerical tests were presented in Section five to support the error analysis.

In year 2010, Xin Cai[31] presented an article “Computational Method for Convection-Dominated Problem”. In this article convection-dominated ordinary differential equation was considered. Asymptotic solution and numerical method are two common methods for solving this kind of equation also, a novel computational method, which combines asymptotic solution, Runge-Kutta method and finite element method, was constructed. The presented method was proved to be an effective computation method. The organization of the article is as following: in first section, authors gave introduction of article and tells, real life problem where convection-dominated diffusion problems are arising. In the next section authors present his considered problem. Decomposition was constructed in section three, with study of Runge-Kutta method. In final section, finite element method was also constructed. The error estimation was given in final section also. In this article, Convection-Dominated problem was considered. The problem will lead to large oscillation since the coefficient of diffusion term is small. Firstly, the analytical solution was decomposed into the smooth component and the singular component. Secondly, Runge-Kutta method is applied to solve the equation outside the boundary layer. At last, Petrov-Galerkin finite element method with piecewise-exponential test function and the piecewise-linear trial function is constructed in order to solve the boundary layer.

7. Conclusions

In the present paper computational methods for solving convection–diffusion problems arising in real life are briefly discussed, it contains and analyzes huge amount of literature related to problems convection-diffusion problems of different types from various fields. This paper is devoted to crux of various research articles published in refereed journals within last five years to get a better know-how of the state of art covering up the subject and will be an excellent reference for researchers to offer a state-of-the-art of most active recent developments of methods for solving convection–diffusion problems with their applications and remaining challenges for such types of problems. After survey of last five year we see that there are many methods required for solving Convection-Diffusion Problems, by using these various methods we can reduce computatniol cast and provide fast convergence.