-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Advances in Life Sciences
p-ISSN: 2163-1387 e-ISSN: 2163-1395
2014; 4(1): 12-16
doi:10.5923/j.als.20140401.02
Concept of Soil Water Movement in Relation to Variable Water Potential
Rajan Bhatt1, Roopinder Singh Gill2, Arsh Alam Singh Gill3
1Department of Soil Science, Punjab Agricultural University, Ludhiana, 141004, India
2Department of Agronomy, Punjab Agricultural University, Ludhiana, 141004, India
3USF Naraingarh, Punjab Agricultural University, Ludhiana, 141004, India
Correspondence to: Rajan Bhatt, Department of Soil Science, Punjab Agricultural University, Ludhiana, 141004, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Soil water potential is the main driving force which causes the soil water to move from one point to other point in the soil depending upon it’s energy state. The total energy state of soil water is defined by its equivalent potential energy, as determined by the various forces acting on the water per unit quantity. In general, flow rates of water in soils is too small to consider kinetic energy. Therefore, the energy state of soil water is defined by its equivalent potential energy, that is by virtue of its position in a force field and which further has a scope to manage irrigation. Usually, farmers mostly apply flood irrigation but after properly monitoring soil water potential with the help of tensiometer helps us to save a significant amount of water. Thus, a proper understanding of soil water potential, it’s components and their relation with the soil water movement is a must for every soil scientist, agronomist and hydrologist for implementing effective plans towards the judicious use of water.
Keywords: Soil water potential, Water movement, Tensiometers, Matric potential
Cite this paper: Rajan Bhatt, Roopinder Singh Gill, Arsh Alam Singh Gill, Concept of Soil Water Movement in Relation to Variable Water Potential, Advances in Life Sciences, Vol. 4 No. 1, 2014, pp. 12-16. doi: 10.5923/j.als.20140401.02.
Article Outline
1. Introduction
- The complex nature of the pore space in soil and the water held therein makes it difficult to specify directly the force fields acting on the water. The description of movement of soil water on a microscopic scale depends upon not only the quantification of the force field but also on the dimensions of the soil matrix geometry. Water is must for all the ecological processes. In Indian Punjab, water scarcity is an emerging problem because of excessive withdrawal of water (13 Lakh ha-m/Year) for the irrigation purposes. With the result out of 141 blocks, 114 blocks in the state declared in the dark zone. Thus, there is urgent need to understand the concept of soil water potential so that some technique must be used for the efficient and judicious irrigation scheduling viz. tensiometer. which schedule applied the irrigation to crops as per soil suction. Tensiometer works on the principle of measuring the soil suction as when soil dries, water from inner of tensiometer porous cup moves out in the soil to make a balance in potential energy of water within cup of tensiometer and the surrounding drying soil. As a result, the potential reading increased in tensiometer and at a predetermined level of potential, irrigation applied to crops. After some time of irrigation, water again move back into the tensiometer from the irrigated soil as now potential is lower in tensiometer cup as compared to the surrounding soil. With this technique neither the grain yield affected (as water applied before the crop faces any water stress) nor excess water applied (as farmer knows that when to irrigate). Water availability in soils is governed by its movement because of the difference in soil water potential at different points, which occurs mainly in unsaturated conditions when only micro-pores are water filled while macro-pores are air filled. On the contrary, however under the saturated soil condition, both macro as well as micro-pores are water filled and conducting water from one place to other. Water under saturated soil conditions moves under the influence of gravity while under unsaturated conditions the difference in water potential is the principle driving force causing the water movement from one point to other point. Micropores of fine textured soils is capable of holding water for a longer duration of time even at higher value of suction while macropores drain out the water quickly at a smaller suction. Thus there is a need for frequent irrigation in coarse textured soil as compared to the fine textured soil.Soil water, like other bodies in nature, can contain energy in different quantities and forms. The potential concept to the soil water in relation to it’s movement was first given by[1] in his classical paper on the capillary potential while[2] showed the dependency of water potential on the water content and[3] prepared tensiometer for measuring it. The study of water movement from its potential (energy state) point of view is not a new concept, but still difficult to understand and is very important for the soil physicist, agronomist and even for the engineers working in the field of water management. Therefore taking it in consideration, this note will helps in understanding the concept of soil water potential, different types of water potentials and one very important fact is that how saturated flow differ from the unsaturated flow.
2. Water Potential
- In the lay man language, water potential is the potential of water to do work as water in soils is present because of their potential i.e height difference (denoted by ψW). It is the difference between the activity of the water molecule in pure distilled water at standard atmospheric conditions of temperature and pressure and activity of the water molecules in any other system viz. soil solution. The activity of water molecule may be greater or lesser than the activity of water molecule in the free water. In the words of International Soil Science Society[4] ψW may be defined as “the amount of work that must be done per unit quantity of pure water in order to transport reversibly and isothermally an infinitesimal quantity of water from a pool of pure water at a specified elevation at atmospheric pressure to the soil water (at the point under consideration)”. So, a reference state must be specified. It can also be defined by knowing the chemical potential of water in a non-electrolytic solution which depends upon (i) Mean free energy per molecule (Value of Avogadro Number) and concentration of water molecule i.e mole fraction of water molecule. Addition of salts in pure water reduces its chemical potential and the degree of this decrease can be expressed as
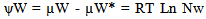 | (1) |
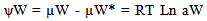 | (2) |
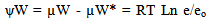 | (3) |
 Among all the units, weight units are more convenient to useTypes of potentials
Among all the units, weight units are more convenient to useTypes of potentials 2.1. Gravitational Potential (ψg)
- On considering weight as the unit of quantity of water, (ψg) comes out to be the vertical distance of elevation between point in question and the reference point and is thus considered as the elevation distance of the point relative to some arbitrary reference level. To raise an object against the gravitational force of attraction work must be expended and this work is stored in the form of gravitational potential energy by the raised body. Gravitational potential is 0 at the reference level, positive above and negative below the reference level. It does not depend upon soil properties, this is the reason why ψg is not considered while calculating the water potential. However, ψg played an important role and is considered while calculating the total water potential as
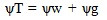 | (4) |
2.2. Matric Potential (ψm)
- Matric potential in soil is because of the adsorption forces of the soil matrix. The greater is the adsorption forces, more is the matric adsorption forces and thus less free is the water. This is why sandy soils drained out quickly at a smaller suction as compared to the clayey soil because clayey soils have greater matric adsorption forces which holds the water tightly and will not allowed the water to drain out quickly. ψm has been considered as capillary potential. If we consider weight as the unit for expressing the unit quantity of water, then ψm at a particular point is the vertical distance between that point in the soil and water surface in manometer filled with water. Generally the ψm results from the two processes, which cannot be separated, since the capillary “wedges” are at a state of internal equilibrium with the adsorption “films” and the one cannot be changed wth out affecting the others. Relation in between saturated hydraulic conductivity and matric potential in texturally divergent soils could be explained through following figure 1 which clearly depicts that saturated conductivity of sandy soil is more than clayey soil, however the unsaturated conductivity of sandy soil decreases more steeply by increasing the suction and decreased from the clayey soils.Matric potential is the dynamic property of soil and is greatly affected by the properties of soils such as clayey soil has more –ve values of ψm as compared to that of sandy soils depicting the greater water holding capacity of clayey soils. Similarly, the soils with higher organic matter (OM) content have higher water content and thus greater –ve value. It is very important to understand that greater is –ve ψm value, higher is the water content as water always moves from the higher potential to lower potential or from lesser –ve to more –ve as more negative values of ψm depicting the lower water content.
 | Figure 1. Relationship between saturated hydraulic conductivity and ψm in the texturally divergent soils |
 | Figure 2. Soil spec in action measuring soil water tension |
|
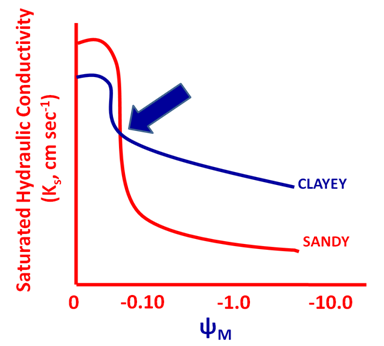
2.3. Pressure Potential (ψp)
 | Figure 3. Deviation in Darcy law when saturated flow become high enough to be turbulent and lesser enough for not to generate any flux |
2.4. Solute Potential (ψs)
- Solute potential arises in the soils because of the presence of salts in soil water and also due to the presence of the semi-permeable layer, which allows only the passage of water through it but not of the salts. In soil-water system, there are two important semi-permeable membranes (i) Cell wall in the roots and (ii) air-water interface. Air-water interphase behaves near to the perfect semi-permeable membrane while cell wall of roots is not a perfect semi-permeable membrane as it allows passage of salts as well as water through it. However, while studying liquid water flow in soils ψs is an unimportant potential due to lack of semi-permeable membrane in it while in plants it is of much importance as plant confort to obsorb water is greatly effected by ψs as more the value of ψs, more the energy the plant have to exert to withdraw water from soils. Consider a salty soil, through which the plant have to exert the water, then it can exert a ψs equal to the permanent wilting point of soils. Thus to determine the value of ψs.ψs = -RT Cs, where R is universal gas constant i.e 82 bars cm-2, T is absolute temperature and Cs is the solute/salt concentration in soils which is most difficult to determine as it also include those species which dissociate into the ions.
2.5. Hydraulic Potential (ψh)
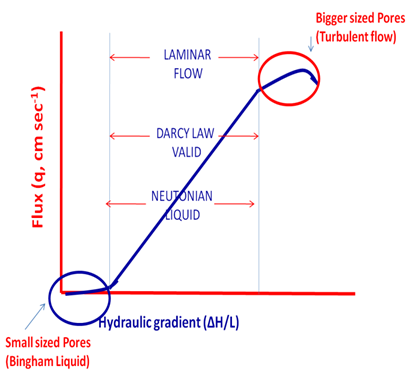
- The ψh is the total water potential i.e ψt which is the sum of ψm + ψp+ ψg. The sum of ψm + ψp+ ψg gives us the idea regarding the direction of water movement in soils however if ψh same throughout the soil profile then the water will not move at all in the soils. Normally under the unsaturated soils, the water moves from the lesser negative potential to the higher value of negative potential.Hydaulic conductivity of a soil is the slope of the curve between flux (discharge per unit area per unit time) and the hydraulic gradient and it varies with texturally divergent soils (Fig 4). This figure explains why movement of water differ in texturally divergent soils and we could manage our cultivation and management practices so as increase the water use efficiency.
 | Figure 4. Relationship between flux and hydraulic gradient in three texturally divergent soils |
3. Conclusions
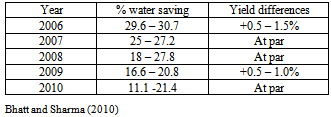
- Declining underground water levels and water productivity (because of excessive water withdrawl from ground about 13 lakh ha-m) is an emerging issue in front of the farmers of the state which needs to be addressed. Faulty and frequent irrigations are responsible for that. The concept of soil water potential is of great importance for uplifting declining underground water table in region. It’s proper utilization and measurement (with tensiometers) is of great value in scheduling irrigation which guides us raegarding when to irrigate. Usually farmers don’t know when to irrigate his crops. Tensiometer measured the varying soil water potential and guide the farmers exactly when to irrigate. Tensiometer based irrigation helps farmers to save upto 30% of the irrigation water which further helps him to increase the water productivity in the region[10]. Thus concept of soil water potential is of great importance as it replaces the arbitrary categorization which earlier used to classify gravitational water, capillary water and hygroscopic water. Thus, finally we conclude that potential difference between the two points in the soil is the main driving force for the movement of water in the soil, which needs to be studied and understand in detail while planning, documenting and implementing any project dealing with the water movement in soil.
ACKNOWLEDGEMENTS
- The author would like to thank Punjab Agricultural University, Ludhiana, Punjab, India which provide him an opportunity to commence his Ph.D programme in field of soil science.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML