-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Algorithms Research
p-ISSN: 2324-9978 e-ISSN: 2324-996X
2019; 5(1): 11-18
doi:10.5923/j.algorithms.20190501.02

A Stochastic Bicriteria Procedure for Creating System Options
Julian Scott Yeomans
OMIS Area, Schulich School of Business, York University, Toronto, M3J 1P3, Canada
Correspondence to: Julian Scott Yeomans, OMIS Area, Schulich School of Business, York University, Toronto, M3J 1P3, Canada.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Stochastic systems are often overwhelmed by incompatible performance requirements and inconsistent performance specifications that can be difficult to identify when supporting decision models must be constructed. Consequently, it is often advantageous to create a set of dissimilar options that afford distinctive approaches to the problem. These alternatives should satisfy the required system performance criteria and yet be maximally different from each other in their decision spaces. This paper describes a stochastic bicriteria procedure that can generate sets of maximally different alternatives. This stochastic algorithmic approach is both computationally efficient and simultaneously produces the prescribed number of maximally different solution alternatives in a single computational run of the procedure.
Keywords: Bicriteria objectives, Stochastic systems, Alternative generation
Cite this paper: Julian Scott Yeomans, A Stochastic Bicriteria Procedure for Creating System Options, Algorithms Research , Vol. 5 No. 1, 2019, pp. 11-18. doi: 10.5923/j.algorithms.20190501.02.
Article Outline
1. Introduction
- Stochastic systems frequently possess structural specifications that are hard to represent mathematically [1-5]. While “optimal” conditions can be calculated for the mathematical formulations, whether these solutions are actually the best for the original “real” system design conditions is far less certain [1], [2], [6]. To improve the decision-making process when faced with such ambiguities, it often proves preferable to propose a few dissimilar options that represent different system perspectives [3], [7]. To be beneficial to the system designers, these distinct options need to be close-to-optimal with respect to their mathematically modelled objective(s), but maximally different from each other within the solution space [6-8]. The primary purpose behind this alternative generation approach is to construct a set of dissimilar options that are “good” when evaluated with respect to the specified system objective(s), but which are fundamentally different from each other in the decision domain. The system designers then need to perform a subsequent assessment of this set of alternatives to determine which specific option(s) most closely satisfy their situation. Consequently, this approach is considered as a decision support method rather than as the solution creation process assumed in “normal” mathematical optimization.Earlier option formulation approaches employed a straightforward process in which each alternative was incrementally constructed by re-running the solution creation algorithm whenever a new option needed to be produced [6-10]. These iterative procedures mimicked the seminal approach in [8] where, after the initial mathematical model had been optimized, all supplementary alternatives were produced one-at-a-time. These incremental approaches all employed n+1 computational iterations – initially to optimize the original problem, then to produce each of the subsequent n alternatives [7], [11-18]. Subsequently, it was demonstrated how a set of maximally different alternatives could be efficiently generated using any population-based algorithm by permitting the generation of the overall optimal solution together with n distinct alternatives in a single computational run irrespective of the value of n [19-23]. In [24] a data structure was created that permits alternatives to be constructed simultaneously by population-based solution methods.In this paper, it is demonstrated how a set of maximally different system design options can be produced by extending several earlier techniques into stochastic optimization ([12-18]). This stochastic approach advances the earlier procedures ([13,15-18]) by permitting the simultaneous generation of n distinct alternatives in a single computational run. Namely, to construct the requisite n maximally different system design options, the algorithm has to run only once irrespective of the value of n [19-23]. Furthermore, a bicriteria, max-sum, max-min objective is employed that combines the novel data structure into the simultaneous solution algorithm. The efficacy of this approach is illustrated on a water resources management system case study.
2. Generating Distinct Solution Options
- Mathematical programming has focused almost exclusively on finding single optimal solutions to single-objective problems or, equivalently, producing noninferior solutions to multi-objective formulations [2], [5], [8]. While these approaches may solve the formulations as constructed mathematically, whether these solutions are truly “best” for the original “real world” applications remains less certain [1], [2], [6], [8]. In most “real world” systems, there are countless system specifications that can never be incorporated into the mathematical problem formulation [1], [5]. Unavoidably, the majority of the subjective aspects remain unmodelled and unquantified in the mathematical system formulations. This frequently occurs when final outcomes are decided upon based not only on modelled objectives, but also on more subjective socio-political-economic preferences and stakeholder goals [7]. When unmodelled components are suspected to exist, non-traditional solution approaches are needed for searching the decision space not only for noninferior solutions, but also for sub-optimal possibilities. Specifically, any search for alternatives to problems suspected to possess unmodelled components must concentrate not only on a non-inferior set of solutions, but also necessarily on an explicit exploration of the problem’s inferior solution space. Numerous “real life” instances of these types of modelling situations are illustrated in [6], [8], [9], and [10].To demonstrate the impact of unmodelled objectives on a solution search, assume that the optimal solution to a maximization problem is X* with objective value Z1* [24]. Suppose a second, unmodelled, maximization objective Z2 exists that represents some “politically acceptable” feature. Assume that the solution, Xa, belonging to the 2-objective noninferior set, exists that corresponds to a best compromise solution if both objectives could actually have been simultaneously considered. While Xa would be the best solution to the real problem, in the actual mathematical formulation it would seem inferior to solution X*, since Z1a
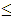 Z1*. Thus, when unmodelled components are included in the decision-making process, inferior decisions to the mathematically modelled system could actually be optimal to the fundamental “real” problem. If unmodelled aspects and unquantified objectives might exist, alternative solution procedures are essential to not only explore the decision region for noninferior solutions to the modelled problem, but also to concurrently search the decision space for explicitly inferior solutions.Necessarily, then, in these situations, the aim is to create a workable set of options that are quantifiably good with respect to the modelled objectives yet are as different as possible from each other within the solution space. By satisfying this maximal difference condition, the resulting set of alternatives is able to supply truly different perspectives that all perform similarly with respect to the known modelled objective(s) yet very differently with respect to various potentially unmodelled aspects. By creating good-but-different options, the system designers are the able to consider potentially desirable qualities within the alternatives that might be able to satisfy the unmodelled objectives to varying degrees of stakeholder acceptability.To motivate the process, it is necessary to formally characterize the mathematical definition of maximal difference [6], [7]. Assume that the optimal solution to an original mathematical programming formulation is X* with corresponding objective value Z* = F(X*). An ensuing difference model can then be solved to produce an alternative solution, X, that is maximally different from X*:
Z1*. Thus, when unmodelled components are included in the decision-making process, inferior decisions to the mathematically modelled system could actually be optimal to the fundamental “real” problem. If unmodelled aspects and unquantified objectives might exist, alternative solution procedures are essential to not only explore the decision region for noninferior solutions to the modelled problem, but also to concurrently search the decision space for explicitly inferior solutions.Necessarily, then, in these situations, the aim is to create a workable set of options that are quantifiably good with respect to the modelled objectives yet are as different as possible from each other within the solution space. By satisfying this maximal difference condition, the resulting set of alternatives is able to supply truly different perspectives that all perform similarly with respect to the known modelled objective(s) yet very differently with respect to various potentially unmodelled aspects. By creating good-but-different options, the system designers are the able to consider potentially desirable qualities within the alternatives that might be able to satisfy the unmodelled objectives to varying degrees of stakeholder acceptability.To motivate the process, it is necessary to formally characterize the mathematical definition of maximal difference [6], [7]. Assume that the optimal solution to an original mathematical programming formulation is X* with corresponding objective value Z* = F(X*). An ensuing difference model can then be solved to produce an alternative solution, X, that is maximally different from X*: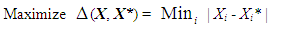 | (1) |
 | (2) |
 | (3) |
3. Stochastic Optimization via Simulation
- Finding optimal solutions to large stochastic problems proves complicated when numerous system uncertainties must be directly incorporated into the solution procedures ([25-28]). In the stochastic optimization via simulation procedures considered in this study, all uncertain parameters, constraints, and objective functions are replaced by simulation models in which the decision variables provide the settings under which simulation is performed. The basic stages can be summarized in the ensuing way ([26], [29]). Assume that the mathematical formulation of the optimization problem consists of n decision variables,
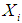 , denoted by the vector
, denoted by the vector 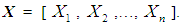 If the objective is given by the function F and the feasible region is designated by D, then the mathematical programming problem is to optimize F(X) subject to X
If the objective is given by the function F and the feasible region is designated by D, then the mathematical programming problem is to optimize F(X) subject to X 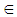 D. When stochastic conditions exist, values for the objective and constraints are determined via simulation. A comparison between two different solutions X1 and X2 requires the evaluation of some statistic of F modelled with X1 compared to the same statistic modelled with X2 ([25], [30]). These statistics are calculated via simulation, in which each X provides the decision variable settings employed in the simulation. While simulation provides the context for comparing results, it does not provide the mechanism for finding optimal solutions to problems. Hence, simulation alone cannot be used for stochastic optimization purposes.Since the measures of system performance are stochastic, each potential solution, X, is evaluated from simulation. Because simulation is computationally intensive, an optimization procedure is used to direct the search for solutions through the problem’s feasible region in as few simulation runs as possible ([27], [30]). As stochastic system problems frequently contain potentially numerous feasible solutions, the quality of the final solution could be exceedingly variable unless an extensive search has been performed throughout all portions of the feasible space. Necessarily, the stochastic optimization method contains two alternating computational phases; (i) an “evolutionary” phase directed by some optimization method (frequently a metaheuristic) and (ii) the solution simulation phase ([31]). Because of the stochastic components, all performance measures are necessarily statistics calculated from the responses generated in the simulation phase. The quality of each solution is found by having its performance criterion, F, evaluated in the simulation phase. After simulating each candidate solution, their respective objective values are returned to the evolutionary phase to be utilized in the creation of the succeeding candidate solutions. Thus, the evolutionary phase aims to advance the system toward improved solutions in subsequent generations and ensures that the solution search does not become trapped in some local optima. After generating new candidate solutions in the evolutionary phase, the new solution set is returned to the simulation phase for comparative evaluation. This alternating, two-phase search process terminates when an appropriately stable system state (i.e. an optimal solution) has been attained. The optimal solution produced by the procedure is the single best solution found throughout the course of the entire search process ([31]).Population-based optimization methods are particularly beneficial for these types of searches because the complete set of candidate solutions maintained within their populations permit searches to be undertaken throughout multiple sections of the feasible region, concurrently. For population-based optimization methods, the evolutionary phase evaluates the entire current population of solutions during each generation of the search and evolves from a current population to a subsequent one. An evolutionary characteristic of population-based procedures is that better solutions in a current population possess a greater likelihood for survival and progression into the subsequent population.It has been shown that this type of optimization-via-simulation approach can be used as a very computationally intensive, stochastic technique ([30], [32]). However, because of the very long computational runs, several approaches to accelerate the search times and solution quality have been explored [29]. The next section introduces a procedure that incorporates simulated stochastic uncertainty to much more efficiently generate sets of maximally different solution options.
D. When stochastic conditions exist, values for the objective and constraints are determined via simulation. A comparison between two different solutions X1 and X2 requires the evaluation of some statistic of F modelled with X1 compared to the same statistic modelled with X2 ([25], [30]). These statistics are calculated via simulation, in which each X provides the decision variable settings employed in the simulation. While simulation provides the context for comparing results, it does not provide the mechanism for finding optimal solutions to problems. Hence, simulation alone cannot be used for stochastic optimization purposes.Since the measures of system performance are stochastic, each potential solution, X, is evaluated from simulation. Because simulation is computationally intensive, an optimization procedure is used to direct the search for solutions through the problem’s feasible region in as few simulation runs as possible ([27], [30]). As stochastic system problems frequently contain potentially numerous feasible solutions, the quality of the final solution could be exceedingly variable unless an extensive search has been performed throughout all portions of the feasible space. Necessarily, the stochastic optimization method contains two alternating computational phases; (i) an “evolutionary” phase directed by some optimization method (frequently a metaheuristic) and (ii) the solution simulation phase ([31]). Because of the stochastic components, all performance measures are necessarily statistics calculated from the responses generated in the simulation phase. The quality of each solution is found by having its performance criterion, F, evaluated in the simulation phase. After simulating each candidate solution, their respective objective values are returned to the evolutionary phase to be utilized in the creation of the succeeding candidate solutions. Thus, the evolutionary phase aims to advance the system toward improved solutions in subsequent generations and ensures that the solution search does not become trapped in some local optima. After generating new candidate solutions in the evolutionary phase, the new solution set is returned to the simulation phase for comparative evaluation. This alternating, two-phase search process terminates when an appropriately stable system state (i.e. an optimal solution) has been attained. The optimal solution produced by the procedure is the single best solution found throughout the course of the entire search process ([31]).Population-based optimization methods are particularly beneficial for these types of searches because the complete set of candidate solutions maintained within their populations permit searches to be undertaken throughout multiple sections of the feasible region, concurrently. For population-based optimization methods, the evolutionary phase evaluates the entire current population of solutions during each generation of the search and evolves from a current population to a subsequent one. An evolutionary characteristic of population-based procedures is that better solutions in a current population possess a greater likelihood for survival and progression into the subsequent population.It has been shown that this type of optimization-via-simulation approach can be used as a very computationally intensive, stochastic technique ([30], [32]). However, because of the very long computational runs, several approaches to accelerate the search times and solution quality have been explored [29]. The next section introduces a procedure that incorporates simulated stochastic uncertainty to much more efficiently generate sets of maximally different solution options.4. Stochastic Bicriteria Algorithm
- In this section, a previously introduced data structure is used that permits the stochastic bicriteria algorithm to be employed for creating system options using any population-based solution algorithm [24], [33-36]. Suppose that the goal is to produce P distinct options in which each individual option possesses n decision variables and the algorithm’s population is to possess K sets of solution alternatives overall. Therefore, each solution in the population contains one complete set of P maximally different alternatives. Let Yk, k = 1,…, K, represent the kth solution consisting of one complete set of P different alternatives. Specifically, if Xkp is the pth alternative, p = 1,…, P, of solution k, k = 1,…, K, then Yk can be represented as
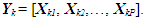 | (4) |
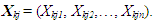 | (5) |
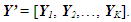 | (6) |
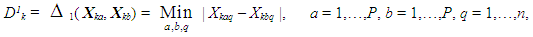 | (7) |
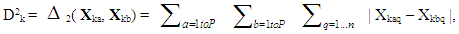 | (8) |
5. Water Resources Case Study
- When faced with situations containing numerous uncertainties, water resources management (WRM) decision-makers often prefer to select from a set of “near best” alternatives that differ significantly from each other in terms of the system structures characterized by their decision variables. The efficacy of the stochastic bicriteria MGA algorithm will be illustrated using a WRM systems case taken from [37]. While this section briefly summarizes the case, more explicit details, data, and descriptions can be found in [37].Maqsood et al. ([37]) previously examined a WRM problem for allocating water in a dry season from an unregulated reservoir to three categories of users: (i) a municipality, (ii) an industrial concern, and (iii) an agricultural sector. The industrial concern and agricultural sector were undergoing significant expansion and needed to know the quantities of water they could reasonably expect. If insufficient water was available, these entities would be forced to curtail their capital expansion plans. If the promised water was delivered, it would contribute positive net benefits to the local economy per unit of water allocated. However, if the water was not delivered, the results would reduce the net benefits to the users.The major problems under these circumstances involved (i) how to effectively allocate water to the three user groups in order to achieve maximum net benefits under the uncertain conditions and (ii) how to incorporate the water policies in terms of allowable amounts within this planning problem with the least risk of system disruption. Included within these decisions is a determination of which one of the multiple possible pathways that the water would flow through in reaching the users. It is further possible to subdivide the various water streams with each resulting substream sent to a different user. Since cost differences from operating the facilities at different capacity levels produce economies of scale, decisions have to be made to determine how much water should be sent along each flow pathway to each user type. Therefore, any single policy option can be composed of a combination of many decisions regarding which facilities received water and what quantities of water would be sent to each user type. All of these decisions were compounded by overriding system uncertainties regarding the seasonal water flows and their likelihoods.The WRM case considers how to effectively allocate the water to the three user groups in order to derive maximum net benefits under the elements of uncertainty and how to incorporate water policies in terms of allowable amounts within this planning problem with the least risk for causing system disruption. Since the uncertainties could be expressed collectively as interval estimates, probability distributions and uncertainty membership functions, the approach of [37] provided a solution for the WRM problem with a net benefit of $2.02 million.In the region studied, the municipal, industrial, and agricultural water demands have been increasing due to population and economic growth. Because of this, it is necessary to ensure that the different water users know where they stand by providing information that is needed to make decisions for various activities and investments. For example, farmers who know there is only a small chance of receiving sufficient water in a dry season are not likely to make major investment in irrigation infrastructure. Similarly, industries are not likely to promote developments of projects that are water intensive knowing that they will have to limit their water consumption. If the promised water cannot be delivered due to insufficiency, the users will have to either obtain water from more expensive alternate sources or curtail their development plans. For example, municipal residents may have to curtail watering of lawns, industries may have to reduce production levels or increase water recycling rates, and farmers may not be able to conduct irrigation as planned. These impacts will result in increased costs or decreased benefits in relation to the regional development. It is thus desired that the available water be effectively allocated to minimize any associated penalties. Thus, the problem can be formulated as maximizing the expected value of the net system benefits. Based upon the local water management policies, a quantity of water can be pre-defined for each user. If this quantity is delivered, it will result in net benefits; however, if not delivered, the system will then be subject to penalties.The WRM authority is responsible for allocating water to each of the municipality, the industrial concerns, and the agricultural sector. As the quantity of stream flows from the reservoir are uncertain, the problem is formulated as a stochastic programming problem. This stochastic programming model can account for the uncertainties in water availability. However, uncertainties may also exist in other parameters such as benefits, costs and water-allocation targets. In the formulation, penalties are imposed when policies that have been expressed as targets are violated. Also, within the model, any uncertain parameter A is represented by
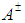 and its corresponding values are generated via probability distributions. To reflect all of these uncertainties, the following stochastic programming model was constructed by [37]:
and its corresponding values are generated via probability distributions. To reflect all of these uncertainties, the following stochastic programming model was constructed by [37]: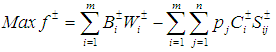 | (9) |
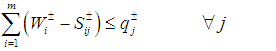 | (10) |
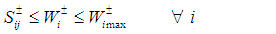 | (11) |
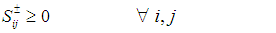 | (12) |
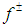 represents the net system benefit ($/m3) and
represents the net system benefit ($/m3) and 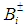 represents the net benefit to user i per m3 of water allocated ($).
represents the net benefit to user i per m3 of water allocated ($). 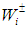 is the fixed allocation amount (m3) for water that is promised to user i, while
is the fixed allocation amount (m3) for water that is promised to user i, while 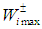 is the maximum allowable amount (m3) that can be allocated to user i. The loss to user i per m3 of water not delivered is given by
is the maximum allowable amount (m3) that can be allocated to user i. The loss to user i per m3 of water not delivered is given by 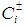 , where
, where 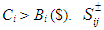 corresponds to the shortage of water, which is the amount (m3) by which Wi is not met when the seasonal flow is qj.
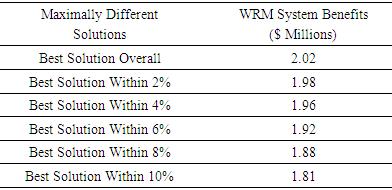
corresponds to the shortage of water, which is the amount (m3) by which Wi is not met when the seasonal flow is qj. 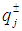 is the amount (m3) of seasonal flow with pj probability of occurrence under j flow level, where pj provides the probability (%) of occurrence of flow level j. The variable i, i = 1, 2, 3, designates the water user, where i = 1 for municipal, 2 for industrial, and 3 for agricultural. The value of j, j = 1, 2, 3, is used to delineate the flow level, where j = 1 represents low flows, 2 represents medium flows, and 3 represents high flows. Finally, m is the total number of water users and n is the total number of flow levels.WRM planners faced with difficult and controversial choices generally prefer to select from a set of near-optimal alternatives that differ significantly from each other in terms of their system structures. In order to create these alternative planning options for the WRM system, it would be possible to place extra target constraints into the original model which would force the generation of solutions that were different from their respective, initial optimal solutions. Suppose for example that five additional planning alternative options were created through the inclusion of a technical constraint on the objective function that decreased the total system benefits of the original model from 2% up to 10% in increments of 2%. By adding these incremental target constraints to the original SO model and sequentially resolving the problem 5 times, it would be possible to create a specific number of alternative policies for WRM planning.However, to improve upon the process of running five separate additional instances of the computationally intensive SO algorithm to generate these solutions, the population-based, dual-criterion MGA procedure described in the previous section was run only once, thereby producing the 5 additional alternatives shown in Table 1. The table shows the overall system benefits for the 5 maximally different options generated. Given the performance bounds established for the objective in each problem instance, the decision-makers can feel reassured by the stated performance for each of these options while also being aware that the perspectives provided by the set of dissimilar decision variable structures are as different from each other as is feasibly possible. Hence, if there are stakeholders with incompatible standpoints holding diametrically opposing viewpoints, the policy-makers can perform an assessment of these different options without being myopically constrained by a single overriding perspective based solely upon the objective value.
is the amount (m3) of seasonal flow with pj probability of occurrence under j flow level, where pj provides the probability (%) of occurrence of flow level j. The variable i, i = 1, 2, 3, designates the water user, where i = 1 for municipal, 2 for industrial, and 3 for agricultural. The value of j, j = 1, 2, 3, is used to delineate the flow level, where j = 1 represents low flows, 2 represents medium flows, and 3 represents high flows. Finally, m is the total number of water users and n is the total number of flow levels.WRM planners faced with difficult and controversial choices generally prefer to select from a set of near-optimal alternatives that differ significantly from each other in terms of their system structures. In order to create these alternative planning options for the WRM system, it would be possible to place extra target constraints into the original model which would force the generation of solutions that were different from their respective, initial optimal solutions. Suppose for example that five additional planning alternative options were created through the inclusion of a technical constraint on the objective function that decreased the total system benefits of the original model from 2% up to 10% in increments of 2%. By adding these incremental target constraints to the original SO model and sequentially resolving the problem 5 times, it would be possible to create a specific number of alternative policies for WRM planning.However, to improve upon the process of running five separate additional instances of the computationally intensive SO algorithm to generate these solutions, the population-based, dual-criterion MGA procedure described in the previous section was run only once, thereby producing the 5 additional alternatives shown in Table 1. The table shows the overall system benefits for the 5 maximally different options generated. Given the performance bounds established for the objective in each problem instance, the decision-makers can feel reassured by the stated performance for each of these options while also being aware that the perspectives provided by the set of dissimilar decision variable structures are as different from each other as is feasibly possible. Hence, if there are stakeholders with incompatible standpoints holding diametrically opposing viewpoints, the policy-makers can perform an assessment of these different options without being myopically constrained by a single overriding perspective based solely upon the objective value.
|
6. Conclusions
- Stochastic system design inherently involves unquantifiable structural elements and inconsistent design specifications. These system design problems frequently possess incompatible components that are difficult to incorporate into underlying mathematical decision models. These stochastic models frequently omit certain key system aspects that can significantly impact the appropriateness of their solutions. These omitted features require system designers to somehow incorporate numerous inconsistencies into their decision-making process prior to the final design resolution. When confronted by these incongruencies, it is unlikely that any single solution can satisfy all of the ambiguous system requirements. Consequently, decision support approaches have been created to address the confounding features, while simultaneously retaining enough flexibility to incorporate the inherent system incongruities.This paper has applied a stochastic bicriteria procedure to system design. This computationally efficient algorithm can simultaneously construct entire sets of close-to-optimal, maximally different system design options. The bicriteria objective can efficiently generate the requisite set of good-but-dissimilar options, with each generated solution providing an entirely different perspective for the system. The max-sum objective criteria ensure that the distances between the created options are good in general, while the max-min criteria ensure that the distances between the options are good in the worst case. Since the stochastic algorithm can be applied to a wide range of system design problem, the practicality of this bicriteria algorithm can be extended to wide array of “real world” system applications. These extensions will be examined in future computational studies.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML