Obayomi Abraham Adesoji, Ogunrinde Roseline Bosede
Department of Mathematical Sciences, Faculty of Science, Ekiti State University, Ado-Ekiti, Nigeria
Correspondence to: Ogunrinde Roseline Bosede, Department of Mathematical Sciences, Faculty of Science, Ekiti State University, Ado-Ekiti, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The paper utilized the application of nonstandard methods to create suitable numerical schemes for some initial value problems arising from nonlinear second order oscillator equations. We have applied the technique of Non-local approximation at the grid points and a set of normalized denominator functions to renormalized the discretization functions. The resulting schemes have been used to simulate the original equations and they have been found to have the same monotonic properties as the original equation.
Keywords:
Nonstandard Methods, Renormalization of Discretization Functions, Nonlinear Oscillator Equations, Second Order Ordinary Differential Equations
Cite this paper: Obayomi Abraham Adesoji, Ogunrinde Roseline Bosede, Nonstandard Discrete Models for Some Initial Value Problems Arising from Nonlinear Oscillator Equations, Algorithms Research , Vol. 4 No. 1, 2015, pp. 8-13. doi: 10.5923/j.algorithms.20150401.02.
1. Introduction
A nth order ordinary differential equation of the form: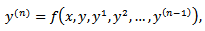
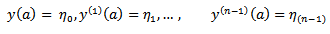 may be solved by reducing it into a system of first order equations and solving the resulting system using any of the suitable classical methods (see Dalquist 1978, Fatunla 1988, Lambert 1991,1993 0. However this approach does not only require in-depth knowledge of functional analysis but it can also be very cumbersome for higher order equations. Moreover it can be discouraging if one consider the effort that will be needed to develop the main program for the scheme and the required sub programs that will be needed to generate predictors and starting values.The approach used by some of these classical researchers is also such that the resultant methods are not continuous and which therefore made it limited in scope and application (Awoyemi 1999). It has also been proved by some eminent scholars that some of these classical methods possess some level of numerical Instability (Mickens 1988, 1994).In this work, we applied the method of renormalization of discretization functions as suggested by Mickens in 1988. Such manipulation of the discretization function to satisfy certain predetermined properties ensure that the resulting discrete model have solutions that replicate the dynamics of the original equation.Renormalization of the discretization function is one of the five point rule proposed by Mickens (1988) to address some short comings of the standard methods, in which the qualitative properties of exact solution are not usually carried along to the numerical solution.We will employ a modification of Mickens strategy in his work on the family of conservative oscillator differential equations of the for my”
may be solved by reducing it into a system of first order equations and solving the resulting system using any of the suitable classical methods (see Dalquist 1978, Fatunla 1988, Lambert 1991,1993 0. However this approach does not only require in-depth knowledge of functional analysis but it can also be very cumbersome for higher order equations. Moreover it can be discouraging if one consider the effort that will be needed to develop the main program for the scheme and the required sub programs that will be needed to generate predictors and starting values.The approach used by some of these classical researchers is also such that the resultant methods are not continuous and which therefore made it limited in scope and application (Awoyemi 1999). It has also been proved by some eminent scholars that some of these classical methods possess some level of numerical Instability (Mickens 1988, 1994).In this work, we applied the method of renormalization of discretization functions as suggested by Mickens in 1988. Such manipulation of the discretization function to satisfy certain predetermined properties ensure that the resulting discrete model have solutions that replicate the dynamics of the original equation.Renormalization of the discretization function is one of the five point rule proposed by Mickens (1988) to address some short comings of the standard methods, in which the qualitative properties of exact solution are not usually carried along to the numerical solution.We will employ a modification of Mickens strategy in his work on the family of conservative oscillator differential equations of the for my” 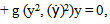 (Mickens 1994). The numerical experiment will involve comparison with the analytic solution.As in the Micken’s rule 2, we proposed that the denominator h be replaced by a function:
(Mickens 1994). The numerical experiment will involve comparison with the analytic solution.As in the Micken’s rule 2, we proposed that the denominator h be replaced by a function: 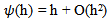 for the first derivative and h2 be replaced by
for the first derivative and h2 be replaced by 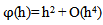 for the second derivative. Moreover the discretization functions were modified in such a way that the characteristic function of the discrete equation decays very fast.
for the second derivative. Moreover the discretization functions were modified in such a way that the characteristic function of the discrete equation decays very fast.
2. Discription of Method and Derivation of the Scheme
The general standard finite difference scheme for second order ordinary differential equation can be derived by replacing the first and second order derivatives in the following manner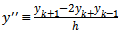 | (1) |
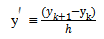 | (2) |
In this nonstandard modification we will adopt the following replacements in line with the rules 2 and 3 of nonstandard modeling rules (Mickens 1994)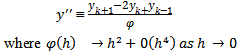 | (3) |
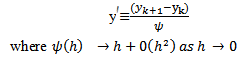 | (4) |
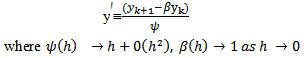 | (5) |
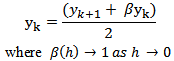 | (6) |
Suitable function for  above include:
above include: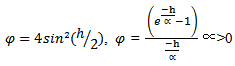 | (7) |
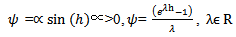 | (8) |
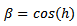 | (9) |
Moreover grid point calculations will be approximated non-locally.A. Example 1 (Zill D. G. 2005)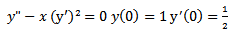 | (10) |
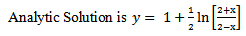 | (11) |
1) Scheme 1 (YNEW1)Using the transformation (3) and (4) for (10) We have the following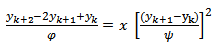 | (12) |
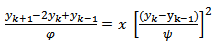 | (13) |
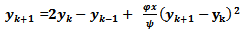 | (14) |
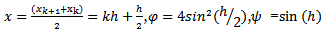
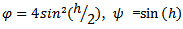 2) Scheme 2 (YNEW2)Using the transformation (3) and (5) for (10)We have the following
2) Scheme 2 (YNEW2)Using the transformation (3) and (5) for (10)We have the following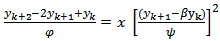 | (15) |
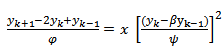 | (16) |
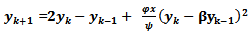 | (17) |
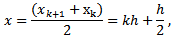
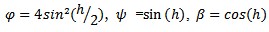 3) Scheme 3 (YNEW3)Using scheme in (17) and another denominator function
3) Scheme 3 (YNEW3)Using scheme in (17) and another denominator function 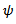 we have
we have 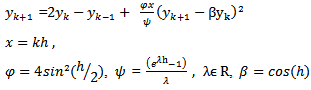 | (18) |
4) Numerical Results for example IThe above schemes were tested using a Fortran script developed for this purpose. Various step sizes were used to compute the results they are presented below:The value of h=1/320 was used because some earlier work on this class of equation has used the same value of h (Awoyemi 1999). In those works values were obtained for only few collocated or interpolated points. The Scheme (YNEW1) was found to be grossly inadequate for this class of equation and so we did not include it in the results.5) Graphical Presentation of Results of Example 1 for h=1/320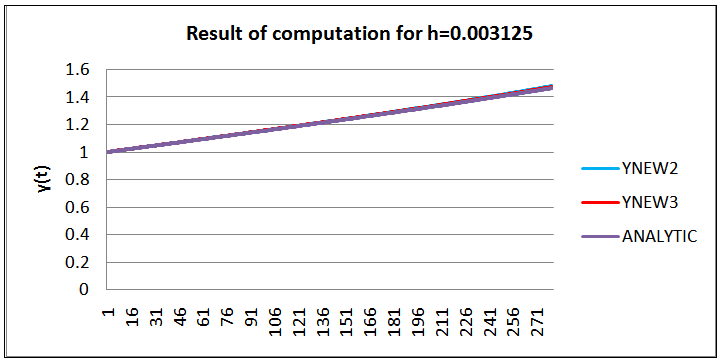 | Figure 1. Graph of the scheme 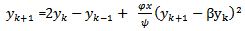 |
 | Figure 2. Absolute error of deviation from 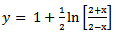 |
6) Graphical presentation of Results of Example 1 for h=0.1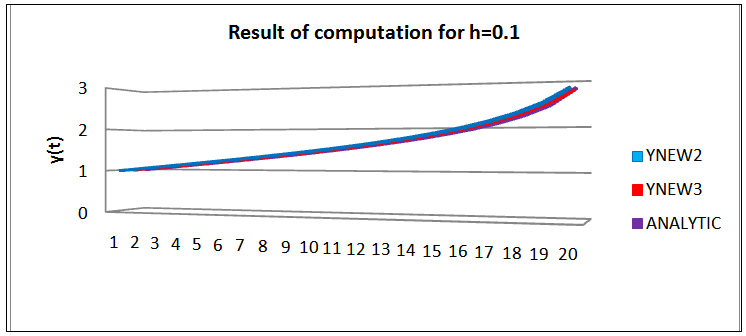 | Figure 3. Graph of the scheme 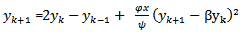 |
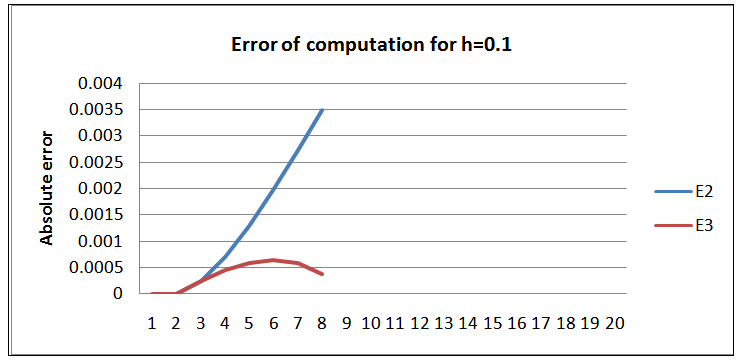 | Figure 4. Absolute error of deviation from 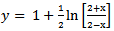 |
B. Example II (Zill D. G. 2005)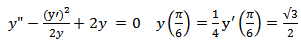 | (19) |
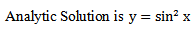 | (20) |
1) Scheme 4 (YNEW4)Using the transformation (3) and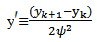 The discrete model of (19) can be written as
The discrete model of (19) can be written as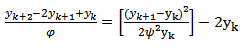 | (21) |
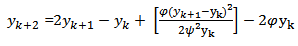 | (22) |
The scheme is equivalent to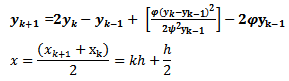 | (23) |
2) Scheme 5 (YNEW5)Use the transformation (3) and 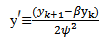 | (24) |
Then (19) can be written as 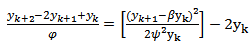 | (25) |
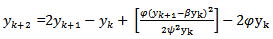 | (26) |
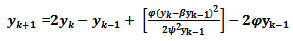 | (27) |
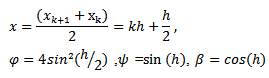 | (28) |
3) Scheme 6 (YNEW6)Using the scheme in (27) and changing the denominator function 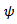 in (28) we have the scheme below
in (28) we have the scheme below 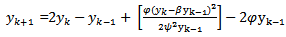 | (29) |
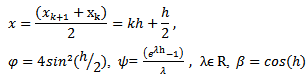 | (30) |
The Scheme (YNEW4) was found to be grossly inadequate for this class of equation and so we did not include it in the results.4) Graphical presentation of Results of Example II for h= 0.003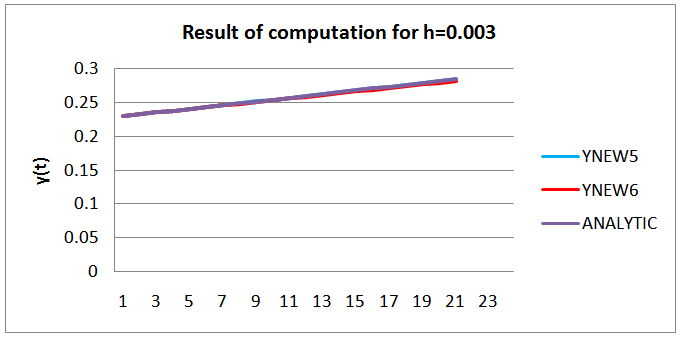 | Figure 5. Graph of the scheme 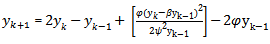 |
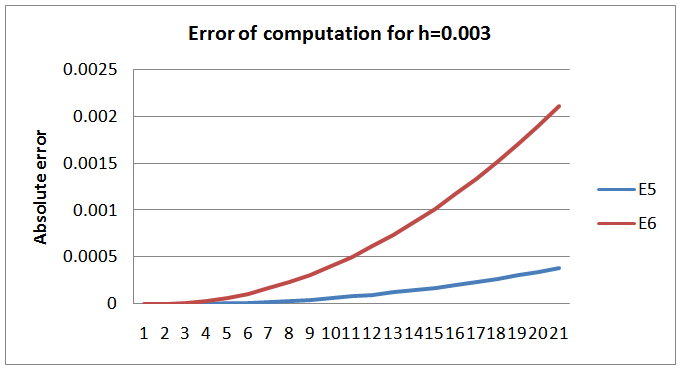 | Figure 6. Absolute error of deviation from 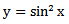 |
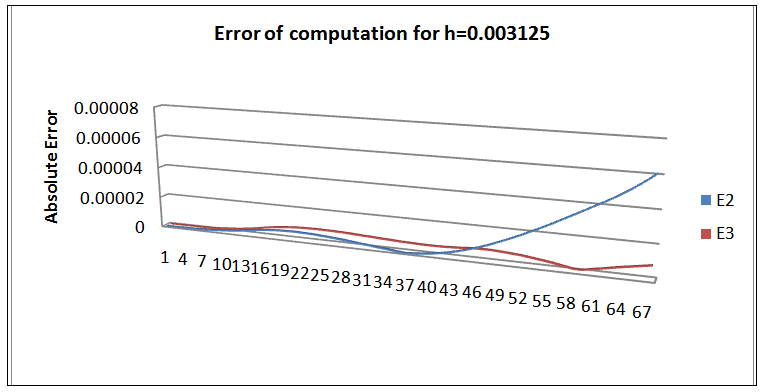
5) Graphical presentation of Results of Example II for h=0.0003125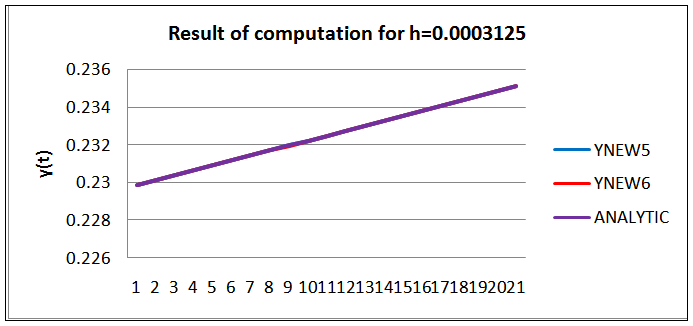 | Figure 7. Graph of the scheme 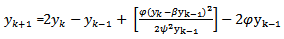 |
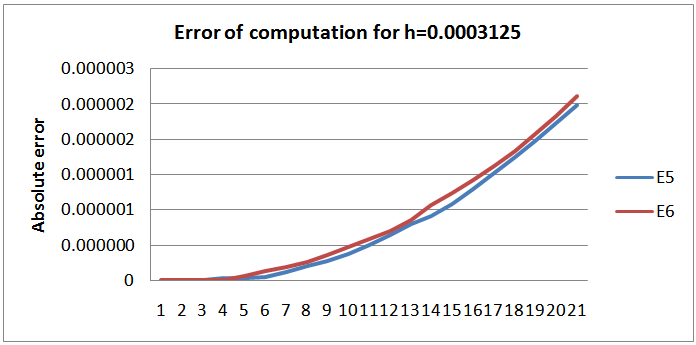 | Figure 8. Absolute error of deviation from 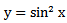 |
3. Conclusions and Discussion
The abysmal performance of the scheme1 on Example 1, 2 and 4, reveal that the straight linear transformation of the non-linear ẏ component is grossly inadequate. We require more analysis of this class of equation so as to design factors that can control the behavior of the schemes in this case. This however supports the claim of Mickens earlier in (1994) on the numerical solution of non-linear conservative oscillators. This method of straight transformation cannot be used for this class of differential equation.We noted that the sixth order scheme of Awoyemi (1999b) perform better at the collocated points in terms of absolute error of calculation. This is a pointer to the need for improvement on construction methodology for nonstandard schemes for this class of equation in the nearest future.The remodeling of the non-linear derivatives contributes immensely to the consistency of the scheme. From the graphs we can conclude that the analytic solution and the numerical solution have the same monotonicity. The scheme therefore carried along the monotonic properties of the original equation. The major achievement of schemes constructed using Mickens Nonstandard rules is that the scheme exhibits the same monotonicity and dynamics as the original equation.We can conclude that the schemes are suitable for numerical approximation of the original equation for small h. The researchers are currently working on the identified weaknesses and restrains.
References
| [1] | R. Anguelov, JMS Lubuma (2003). Nonstandard finite difference method by nonlocal approximation, Mathematics and Computers in simulation 6: 465 -475. |
| [2] | D. O. Awoyemi (1999) A class of continuous Methods for General second Order Initial Value Problems in Ordinary Differential Equations. International Journal of Computer and Mathematics. 72, 29-37. |
| [3] | D. O. Awoyemi (1999) A new Sixth-Order algorithm for General second Order Ordinary Differential Equations. International Journal of Computer and Mathematics. 77, 117-124. |
| [4] | G. Dalquist, (1978) On accuracy and unconditional stability of Linear Equations BIT, 18 pp133-136. |
| [5] | S. O. Fatunla (1988) Numerical Methods for Initial Value Problems in Ordinary Differential Equations, Academic press. |
| [6] | Mickens R.E. (1994). Nonstandard Finite Difference Models of Differential Equations, World Scientific, Singapore.Pp. 1-115, 144-162. |
| [7] | Zill D G, Cullen R M (2005) Differential Equations with boundary value problems (sixth Edition) Brooks /Cole Thompson Learning Academic Resource Center. Pp. 40-112, 367-387. |

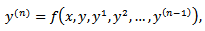
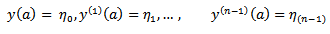 may be solved by reducing it into a system of first order equations and solving the resulting system using any of the suitable classical methods (see Dalquist 1978, Fatunla 1988, Lambert 1991,1993 0. However this approach does not only require in-depth knowledge of functional analysis but it can also be very cumbersome for higher order equations. Moreover it can be discouraging if one consider the effort that will be needed to develop the main program for the scheme and the required sub programs that will be needed to generate predictors and starting values.The approach used by some of these classical researchers is also such that the resultant methods are not continuous and which therefore made it limited in scope and application (Awoyemi 1999). It has also been proved by some eminent scholars that some of these classical methods possess some level of numerical Instability (Mickens 1988, 1994).In this work, we applied the method of renormalization of discretization functions as suggested by Mickens in 1988. Such manipulation of the discretization function to satisfy certain predetermined properties ensure that the resulting discrete model have solutions that replicate the dynamics of the original equation.Renormalization of the discretization function is one of the five point rule proposed by Mickens (1988) to address some short comings of the standard methods, in which the qualitative properties of exact solution are not usually carried along to the numerical solution.We will employ a modification of Mickens strategy in his work on the family of conservative oscillator differential equations of the for my”
may be solved by reducing it into a system of first order equations and solving the resulting system using any of the suitable classical methods (see Dalquist 1978, Fatunla 1988, Lambert 1991,1993 0. However this approach does not only require in-depth knowledge of functional analysis but it can also be very cumbersome for higher order equations. Moreover it can be discouraging if one consider the effort that will be needed to develop the main program for the scheme and the required sub programs that will be needed to generate predictors and starting values.The approach used by some of these classical researchers is also such that the resultant methods are not continuous and which therefore made it limited in scope and application (Awoyemi 1999). It has also been proved by some eminent scholars that some of these classical methods possess some level of numerical Instability (Mickens 1988, 1994).In this work, we applied the method of renormalization of discretization functions as suggested by Mickens in 1988. Such manipulation of the discretization function to satisfy certain predetermined properties ensure that the resulting discrete model have solutions that replicate the dynamics of the original equation.Renormalization of the discretization function is one of the five point rule proposed by Mickens (1988) to address some short comings of the standard methods, in which the qualitative properties of exact solution are not usually carried along to the numerical solution.We will employ a modification of Mickens strategy in his work on the family of conservative oscillator differential equations of the for my” 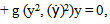 (Mickens 1994). The numerical experiment will involve comparison with the analytic solution.As in the Micken’s rule 2, we proposed that the denominator h be replaced by a function:
(Mickens 1994). The numerical experiment will involve comparison with the analytic solution.As in the Micken’s rule 2, we proposed that the denominator h be replaced by a function: 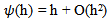 for the first derivative and h2 be replaced by
for the first derivative and h2 be replaced by 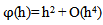 for the second derivative. Moreover the discretization functions were modified in such a way that the characteristic function of the discrete equation decays very fast.
for the second derivative. Moreover the discretization functions were modified in such a way that the characteristic function of the discrete equation decays very fast.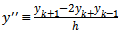
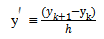
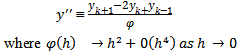
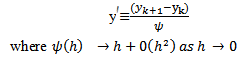
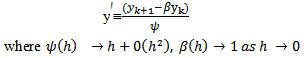
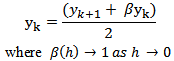
 above include:
above include: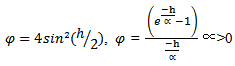
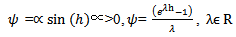
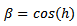
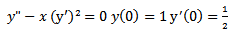
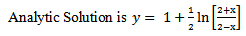
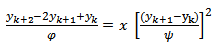
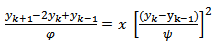
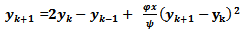
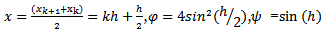
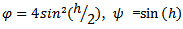 2) Scheme 2 (YNEW2)Using the transformation (3) and (5) for (10)We have the following
2) Scheme 2 (YNEW2)Using the transformation (3) and (5) for (10)We have the following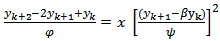
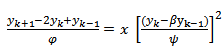
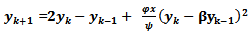
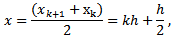
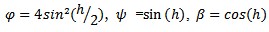 3) Scheme 3 (YNEW3)Using scheme in (17) and another denominator function
3) Scheme 3 (YNEW3)Using scheme in (17) and another denominator function 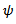 we have
we have 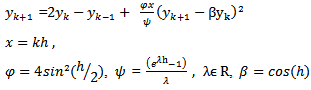

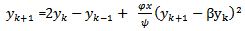

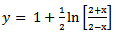

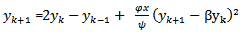

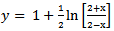
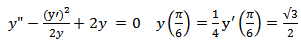
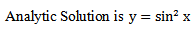
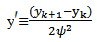 The discrete model of (19) can be written as
The discrete model of (19) can be written as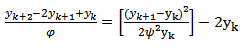
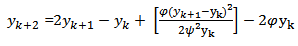
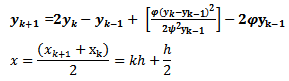
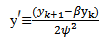
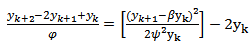
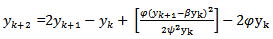
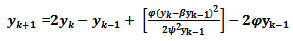
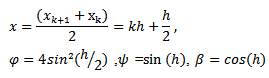
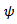 in (28) we have the scheme below
in (28) we have the scheme below 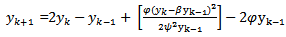
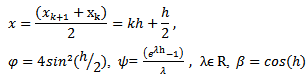

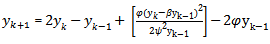

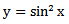

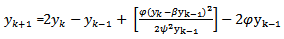

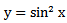
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML