-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Algorithms Research
p-ISSN: 2324-9978 e-ISSN: 2324-996X
2015; 4(1): 1-7
doi:10.5923/j.algorithms.20150401.01
Solution of P versus NP problem
Mustapha Hamidi
Meknes, Morocco
Correspondence to: Mustapha Hamidi , Meknes, Morocco.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This paper, taking Travelling Salesman Problem as our object, wishes to develop a constructive algorithm to prove P=NP. Our algorithm is described as this process: initially, constructing a convex polygon that includes all points and creating a special centroid of this convex polygon, next, examine the position of each point compared to the centroid's position; then, repeating the previous step until all vertexes are included into the optimal tour. This paper has shown that our constructive algorithm can solve the Travelling Salesman Problem in polynomial time.
Keywords: NP-complete problems, Travelling salesman problem, Algorithm, Distance, Point, Convex polygon, Triangle, Special Centroid
Cite this paper: Mustapha Hamidi , Solution of P versus NP problem, Algorithms Research , Vol. 4 No. 1, 2015, pp. 1-7. doi: 10.5923/j.algorithms.20150401.01.
1. Introduction
- This paper, taking Travelling Salesman Problem as our object, wishes to develop a constructive algorithm to prove P=NP, which is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute, and is also a major unsolved problem in computer science. NP represents the class of questions for which there is no known way to find an answer quickly, but an answer can be verified in polynomial time. For the hardest NP problems (i.e., NP-complete problems), given an efficient algorithm for any one of them, we can find an efficient algorithm for all of them [1-4].The Traveling Salesman Problem (TSP) is the problem of finding a least-cost sequence in which to visit a set of cities, starting and ending at the same city, and in such a way that each city is visited exactly once. This problem has received a tremendous amount of attention over the years due in part to its wide applicability in practice (see [5], for examples). Also, since its seminal formulation as a mathematical programming problem in the 1950's [6], the problem has been at the core of most of the developments in the area of Combinatorial Optimization [7]. A key issue has been the question of whether there exists a polynomial-time algorithm for solving the problem [8].In this paper, we present a polynomial-sized linear programming formulation of the Traveling Salesman Problem (TSP).
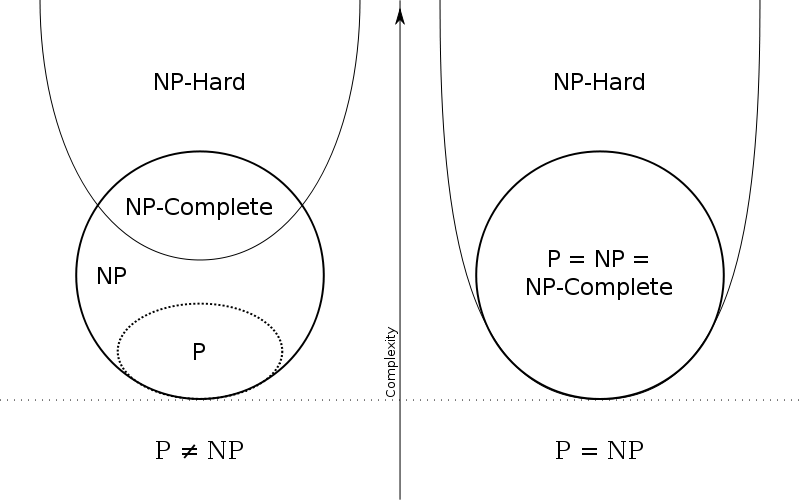 | Figure 1. Euler diagram for P, NP, NP-complete, and NP-hard set of problems |
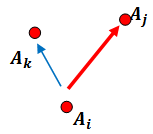
2. Solution’s Idea
 Let G be the special centroid of triangle
Let G be the special centroid of triangle  , which verifies
, which verifies 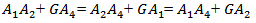 We have
We have 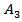 within the triangle
within the triangle 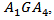 and thus the shortest distance is obtained by connecting
and thus the shortest distance is obtained by connecting 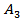 to
to 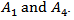 àTherefore the shortest path is
àTherefore the shortest path is 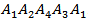 . It describes the main concept of the solution.
. It describes the main concept of the solution. 3. Algorithm
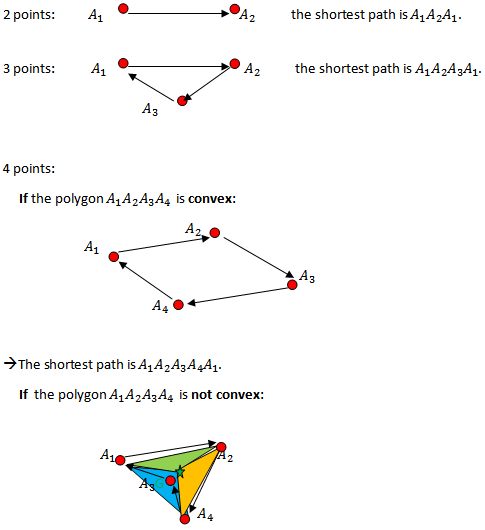
- Let n be a number of points
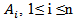 ; and let
; and let 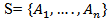 be a set of these points.We want to calculate the minimum distance between these points by returning to the starting point.
be a set of these points.We want to calculate the minimum distance between these points by returning to the starting point.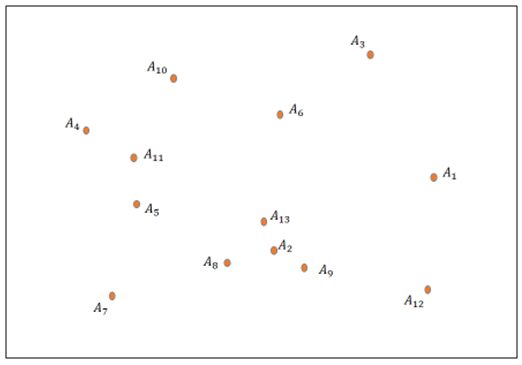 | Figure 2. Distribution of points for which we want to calculate a minimum distance by returning to the starting point |
 Determinant:Mathematically, a simple calculation suffices as the determinant.We have points
Determinant:Mathematically, a simple calculation suffices as the determinant.We have points  .Let D be the vector
.Let D be the vector 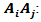 Determining the polygon containing the points of the set
Determining the polygon containing the points of the set 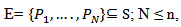 where
where 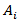 gives :
gives :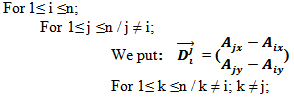
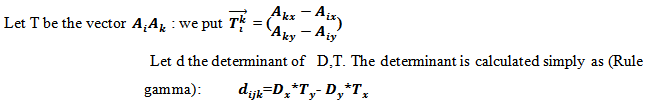
 Thus the convex polygon is as shown in Figure 3.
Thus the convex polygon is as shown in Figure 3.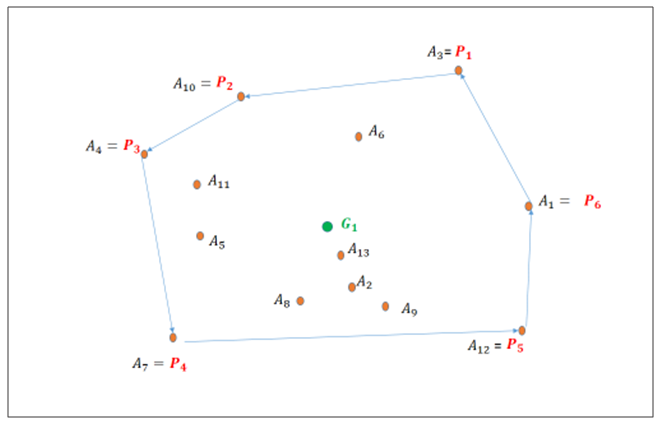 | Figure 3. Creation of convex polygon that includes all points |
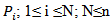 are the points belonging to the convex polygon.Let G be the special centroid of the polygon, which verifies:
are the points belonging to the convex polygon.Let G be the special centroid of the polygon, which verifies:
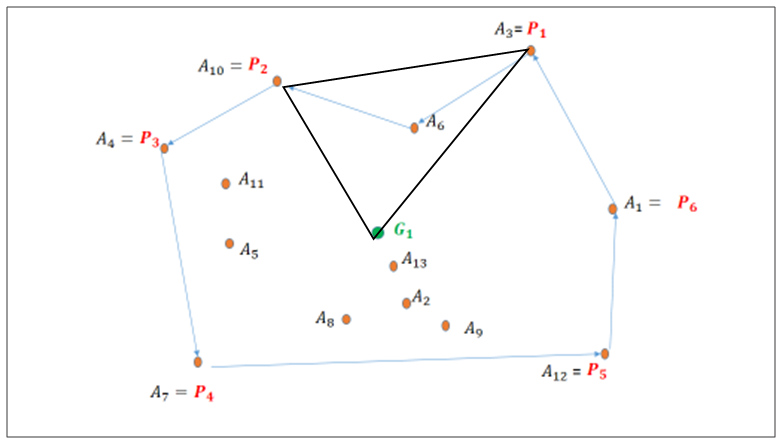 | Figure 4. One point in the triangle  |
 is alone in the triangle, then
is alone in the triangle, then 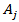 is connected to
is connected to 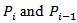 (Figure 4). - If there are two points
(Figure 4). - If there are two points 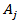 and
and 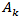 , 1≤ j ≤ n and 1≤ k ≤ n within the triangle (Figure 5), then: - If
, 1≤ j ≤ n and 1≤ k ≤ n within the triangle (Figure 5), then: - If 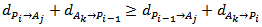 then
then 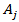 is connected to
is connected to  . - Otherwise
. - Otherwise  will be connected to
will be connected to  and
and .
.  | Figure 5. Two points in the triangle  |
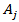 within the triangle
within the triangle 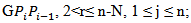 we compose the convex polygon between the points
we compose the convex polygon between the points 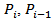 that includes points
that includes points 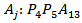 (Figure 6). Therefore, there are M points forming a set
(Figure 6). Therefore, there are M points forming a set  .
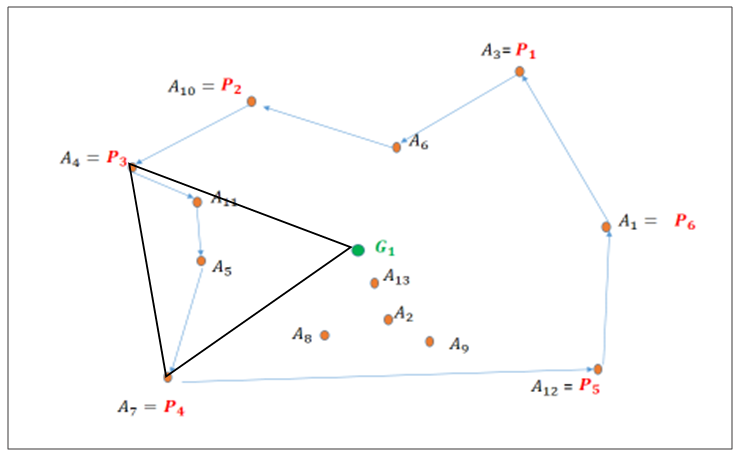
.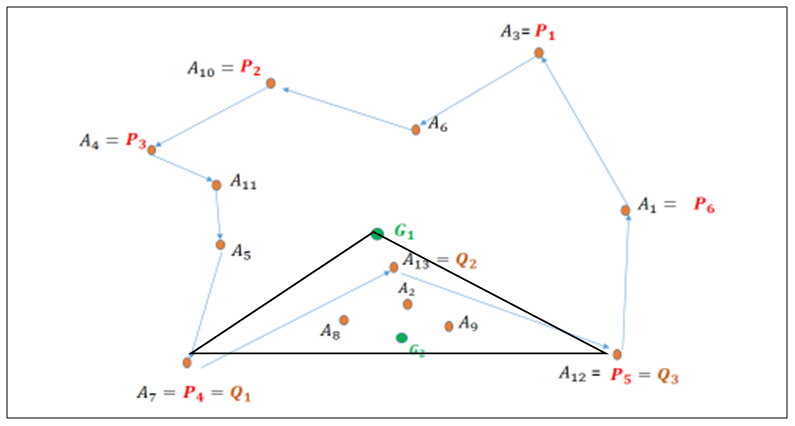 | Figure 6. Many points in the triangle  , thus we create a new convex polygon within the triangle , thus we create a new convex polygon within the triangle 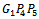 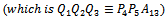 and its centroid and its centroid 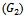 |
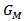 , a centroid of M points, and apply the same method as above (from
, a centroid of M points, and apply the same method as above (from  ) until all point of triangle
) until all point of triangle 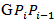 are included into the optimal tour, and then proceed to point
are included into the optimal tour, and then proceed to point 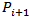 .
.  | Figure 7. One point in the triangle  |
 | Figure 8. Two points in the triangle 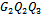 |
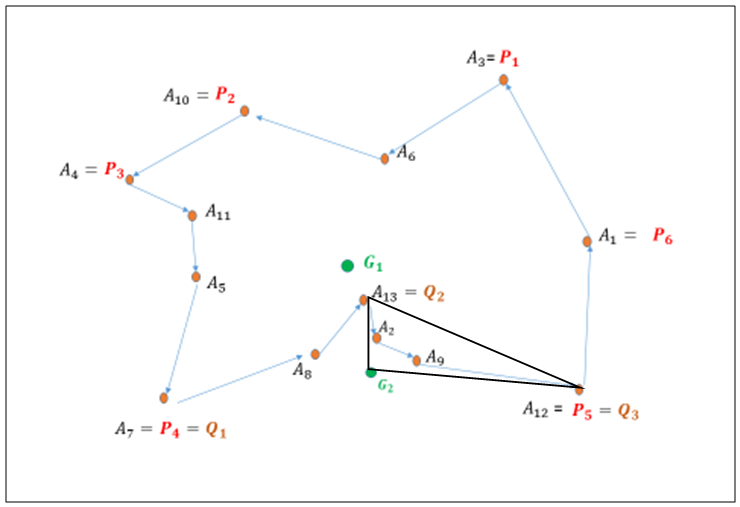
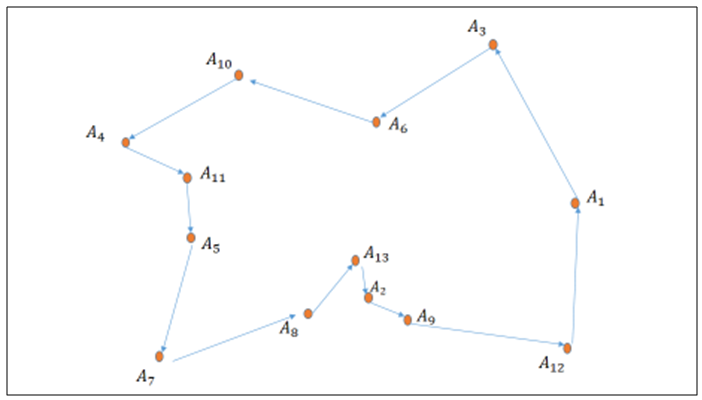 | Figure 9. Optimal path |
4. Discussion
- To understand the importance of the P versus NP problem let us imagine a world where P=NP. Technically we could have P = NP, but not have practical algorithms for most NP-complete problems. But suppose in fact we do have very quick algorithms for all these problems.Many focus on the negative, that if P = NP then public-key cryptography becomes impossible. True, but what we will gain from P = NP will make the whole Internet look like a footnote in history.Since all the NP-complete optimization problems become easy, everything will be much more efficient. Transportation of all forms will be scheduled optimally to move people and goods around quicker and cheaper. Manufacturers can improve their production to increase speed and create less waste. Learning becomes easy by using the principle of Occam's razor—we simply find the smallest program consistent with the data. Near perfect vision recognition, language comprehension and translation and all other learning tasks become trivial. We will also have much better predictions of weather and earthquakes and other natural phenomenon.P = NP would also have big implications in mathematics. One could find short, fully logical proofs for theorems but these proofs are usually extremely long. But we can use the Occam razor principle to recognize and verify mathematical proofs as typically written in journals. We can then find proofs of theorems that have reasonable length proofs say in under 100 pages. A person who proves P = NP would walk home from the Clay Institute not with $1 million check but with seven (actually six since the Poincaré Conjecture appears solved).
5. Conclusions
- The Travelling Salesman Problem is solvable in polynomial time, and consequently the polynomial solvability of NP-complete problems is stated.The consequences of this solution are considerable in many areas: cryptology, computer science, mathematics, engineering, economics… The implications of the solution may make the resolution of other problems Millennium trivial.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML