-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Algorithms Research
p-ISSN: 2324-9978 e-ISSN: 2324-996X
2013; 2(2): 50-57
doi:10.5923/j.algorithms.20130202.03
Solving Ill Conditioned Linear Systems Using the Extended Iterative Refinement Algorithm: The Forward Error Bound
Abdramane Sermé
Department of Mathematics, The City University of New York, New York, NY, 10007, USA
Correspondence to: Abdramane Sermé, Department of Mathematics, The City University of New York, New York, NY, 10007, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper aims to provide a bound of the forward error of the extended iterative refinement or improvement algorithm used to find the solution to an ill conditioned linear system. We use the additive preconditioning for preconditioner of a smaller rank r and the Schur aggregation to reduce the computation of the solution to an ill conditioned linear system to the computation of the Schur aggregate S. We find S by computing W the solution of a matrix system using an extension of Wikinson iterative refinement algorithm. Some steps of the algorithm are computed error free and other steps are computed with errors that need to be evaluated to determine the accuracy of the algorithm. In this paper we will find the upper bound of the forward error of the algorithm and determine if its solution W can be considered accurate enough.
Keywords: Forward Error Analysis, Ill Conditioned Linear System, Sherman-Morrison-Woodbury (SMW) Formula, Preconditioning, Schur Aggregation, Iterative Refinement or Improvement, Algorithm, Singular Value Decomposition
Cite this paper: Abdramane Sermé, Solving Ill Conditioned Linear Systems Using the Extended Iterative Refinement Algorithm: The Forward Error Bound, Algorithms Research , Vol. 2 No. 2, 2013, pp. 50-57. doi: 10.5923/j.algorithms.20130202.03.
Article Outline
1. Introduction
- We find the solution
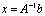 of an ill conditioned linear system
of an ill conditioned linear system 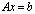 by transforming it using the additive preconditioning and the Schur aggregation. We use the Sherman-Morrison-Woodbury (SMW) formula
by transforming it using the additive preconditioning and the Schur aggregation. We use the Sherman-Morrison-Woodbury (SMW) formula 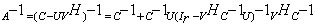 where
where 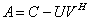 is an invertible square matrix and
is an invertible square matrix and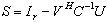 to get new linear systems. The challenge in solving these new linear systems of smaller sizes with well conditioned coefficients matrices
to get new linear systems. The challenge in solving these new linear systems of smaller sizes with well conditioned coefficients matrices 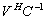 ,
, 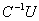 and
and 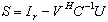 is the computation of the Schur aggregate S. The technique of (extended) iterative refinement or improvement for computing the Schur aggregate[14] and its application for solving linear systems of equations has been studied in a number of papers[3, 15, 18]. Its variant that we used allows us to compute
is the computation of the Schur aggregate S. The technique of (extended) iterative refinement or improvement for computing the Schur aggregate[14] and its application for solving linear systems of equations has been studied in a number of papers[3, 15, 18]. Its variant that we used allows us to compute 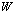 with high precision. The high precision is achieved by minimizing the errors in the computation. The bound of the forward error will allow us to determine if the computed solution is an accurate one. This paper is divided into three sections. The first section covers the concept of rounding errors, floating-point summation, matrix norms and convergence. The second section is devoted to the additive preconditioning, the Schur aggregation and how the iterative refinement or improvement technique is used with the SMW formula to transform the original linear system
with high precision. The high precision is achieved by minimizing the errors in the computation. The bound of the forward error will allow us to determine if the computed solution is an accurate one. This paper is divided into three sections. The first section covers the concept of rounding errors, floating-point summation, matrix norms and convergence. The second section is devoted to the additive preconditioning, the Schur aggregation and how the iterative refinement or improvement technique is used with the SMW formula to transform the original linear system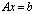 into better conditioned linear systems. The third section analyzes the forward error of the extended iterative refinement or improvement algorithm and provides a forward error bound.
into better conditioned linear systems. The third section analyzes the forward error of the extended iterative refinement or improvement algorithm and provides a forward error bound.2. Rounding Errors, Floating-point Summation, Matrix Norms and Convergence
2.1. Rounding Errors
- Definition 2.1.1 Let
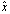 be an approximation of the scalar x. The absolute error in
be an approximation of the scalar x. The absolute error in 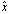 approximating
approximating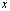 is the number
is the number 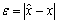 .Definition 2.1.2 Let
.Definition 2.1.2 Let 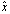 be an approximation of a scalar
be an approximation of a scalar 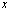 . The absolute and relative errors of this approximation are the numbers
. The absolute and relative errors of this approximation are the numbers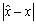 and
and 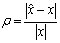 , respectively. If
, respectively. If 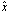 is an approximation to
is an approximation to 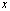 with relative error
with relative error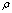 , then there is a number
, then there is a number 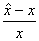 such that 1)
such that 1) 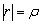 and 2)
and 2) 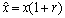 .Remark 2.1.1 The relative error
.Remark 2.1.1 The relative error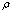 is independent of scaling, that is the scaling
is independent of scaling, that is the scaling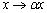 and
and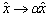 leave
leave 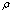 unchanged.Theorem 2.1[6] Assume that
unchanged.Theorem 2.1[6] Assume that 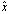 approximates
approximates 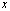 with relative error
with relative error 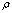 < 1. Then
< 1. Then 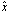 is nonzero and
is nonzero and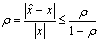 .Remark 2.1.2 If the relative error of
.Remark 2.1.2 If the relative error of 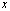 with respect to
with respect to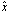 is
is 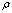 , then
, then 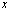 and
and 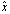 agree to roughly
agree to roughly 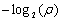 correct significant digits. For binary system, if
correct significant digits. For binary system, if 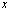 and
and 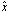 have relative error of approximately
have relative error of approximately 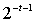 , then
, then 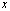 and
and 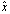 agree to about
agree to about 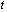 bits.Definition 2.1.3 The componentwise relative error is defined as:
bits.Definition 2.1.3 The componentwise relative error is defined as: 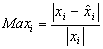 for
for 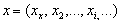 and is widely used in the error analysis and perturbation theory.Remark 2.1.3 In numerical computation, one has three main sources of errors.1. Rounding errors, which are unavoidable consequences of working in finite precision arithmetic.2. Uncertainty in the input data, which is always a possibility when we are solving practical problems.3. Truncation errors, which are constituted and introduced by omitted terms.Rounding errors and Truncation errors are closely related to forward errors.Definition 2.1.4 Precision is the number of digits in the representation of a real number. It defines the accuracy with which the computations and in particular the basic arithmetic operations
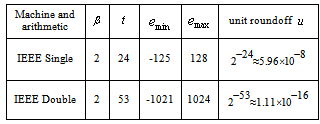
and is widely used in the error analysis and perturbation theory.Remark 2.1.3 In numerical computation, one has three main sources of errors.1. Rounding errors, which are unavoidable consequences of working in finite precision arithmetic.2. Uncertainty in the input data, which is always a possibility when we are solving practical problems.3. Truncation errors, which are constituted and introduced by omitted terms.Rounding errors and Truncation errors are closely related to forward errors.Definition 2.1.4 Precision is the number of digits in the representation of a real number. It defines the accuracy with which the computations and in particular the basic arithmetic operations 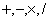 are performed. For floating point arithmetic, precision is measured by the unit roundoff or machine precision, which we denote u in single precision and ū in double precision. The values of the unit roundoff are given in Table 1.1 in Section 2.3.Remark 2.1.4 Accuracy refers to the absolute or relative error of an approximation.Definition 2.1.5 Let
are performed. For floating point arithmetic, precision is measured by the unit roundoff or machine precision, which we denote u in single precision and ū in double precision. The values of the unit roundoff are given in Table 1.1 in Section 2.3.Remark 2.1.4 Accuracy refers to the absolute or relative error of an approximation.Definition 2.1.5 Let 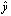 be an approximation of
be an approximation of 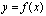 computed with a precision
computed with a precision 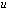 where
where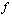 is a real function of a real scalar variable.
is a real function of a real scalar variable. 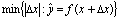 is called the (absolute) backward error, whereas the absolute or relative errors of
is called the (absolute) backward error, whereas the absolute or relative errors of 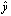 are called forward errors.Definition 2.1.6 For an approximation
are called forward errors.Definition 2.1.6 For an approximation 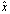 to a solution of a linear system
to a solution of a linear system 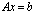 with
with 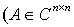 and
and 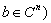 , the forward error is the ratio
, the forward error is the ratio 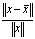 .The process of bounding the forward error of a computed solution in terms of
.The process of bounding the forward error of a computed solution in terms of 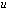 is called forward error analysis.
is called forward error analysis. 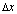 is the perturbation of
is the perturbation of 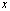 .Definition 2.1.7 An algorithm is called forward stable if it produces answers with forward errors of similar magnitude to those produced by backward stable method.Definition 2.1.8 A mixed forward-backward error is defined by the equation
.Definition 2.1.7 An algorithm is called forward stable if it produces answers with forward errors of similar magnitude to those produced by backward stable method.Definition 2.1.8 A mixed forward-backward error is defined by the equation 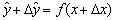 where
where 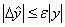 ,
, 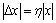 with
with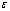 and
and 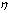 are small constants.Remark 2.1.5 This definition implies that the computed value ŷ differs little from the value
are small constants.Remark 2.1.5 This definition implies that the computed value ŷ differs little from the value 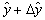 that would have been produced by an input
that would have been produced by an input 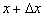 little different from the actual input
little different from the actual input 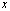 . Simpler,
. Simpler, 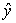 is almost the right answer for almost the right data.Definition 2.1.9 An algorithm is called numerically stable if it is stable in the mixed forward and backward error sense.Remark 2.1.6 A backward stability implies a forward stability but the converse is not true.Remark 2.1.7 One may use the following rule of thumb;Forward error
is almost the right answer for almost the right data.Definition 2.1.9 An algorithm is called numerically stable if it is stable in the mixed forward and backward error sense.Remark 2.1.6 A backward stability implies a forward stability but the converse is not true.Remark 2.1.7 One may use the following rule of thumb;Forward error 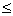 condition number
condition number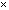 backward error, with approximate equality possible. Therefore the computed solution to an ill conditioned problem can have a large forward error even if the computed solution has a small backward error. This error can be amplified by the condition number in the transition to forward error. This is one of our motivations for reducing the condition number of the matrix A using the additive preconditioning method.Definition 2.1.10 For a system of linear equations
backward error, with approximate equality possible. Therefore the computed solution to an ill conditioned problem can have a large forward error even if the computed solution has a small backward error. This error can be amplified by the condition number in the transition to forward error. This is one of our motivations for reducing the condition number of the matrix A using the additive preconditioning method.Definition 2.1.10 For a system of linear equations 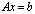 ,
, 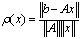 is called the relative residual. The relative residual gives us an indication on how closely
is called the relative residual. The relative residual gives us an indication on how closely 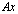 represents
represents 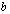 and is scale independent.
and is scale independent.2.2. Floating-point Number System
- Definition 2.2.1[6] A floating-point number system
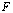 is a subset of the real numbers whose elements have the form
is a subset of the real numbers whose elements have the form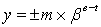 . The range of the nonzero floating-point numbers in
. The range of the nonzero floating-point numbers in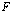 is given by
is given by 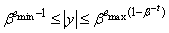 . Any floating-point number
. Any floating-point number 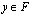 can be written in the form
can be written in the form 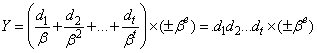 where each digit
where each digit 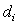 satisfies
satisfies 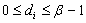 and
and 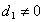 for normalized numbers.
for normalized numbers. 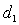 is called the most significant digit and
is called the most significant digit and 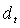 the least significant digit.
the least significant digit.2.3. Error-free Floating-point Summation
- Here is a summation algorithm due to D.E. Knuth[7]. Algorithm 1. Error-free transformation of the sum of two floating point numbers
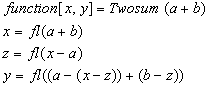 The algorithm transforms two input-floating point numbers
The algorithm transforms two input-floating point numbers 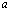 and
and 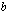 into two output floating-point numbers
into two output floating-point numbers 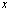 and
and 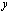 such that
such that 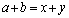 and
and 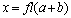 . The same solution is achieved using the Kahan-Babušhka’s[11] and Dekker’s[12] classical algorithm provided that
. The same solution is achieved using the Kahan-Babušhka’s[11] and Dekker’s[12] classical algorithm provided that 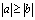 . It uses fewer ops but includes branches, which slows down the code optimization outputs.Definition 2.3.1[8] The unit roundoff error
. It uses fewer ops but includes branches, which slows down the code optimization outputs.Definition 2.3.1[8] The unit roundoff error 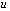 is the quantity
is the quantity 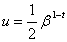 . We write
. We write 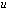 and
and 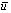 to denote the operations performed in single precision and in double precision, respectively.
to denote the operations performed in single precision and in double precision, respectively.
|
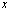 lying in
lying in 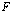 can be approximated by an element of
can be approximated by an element of 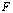 with a relative error no larger than
with a relative error no larger than 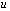 .Theorem 2.2 If
.Theorem 2.2 If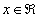 lies in
lies in 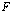 then
then 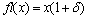 with
with 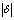 <
< 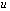 Theorem 2.2 says that
Theorem 2.2 says that 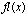 is equal to
is equal to 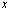 multiplied by a factor very close to 1.Definition 2.3.2 From now on
multiplied by a factor very close to 1.Definition 2.3.2 From now on 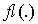 , for an argument that is an arithmetic expression, denotes the computed value of that expression. op represents floating-point operation in
, for an argument that is an arithmetic expression, denotes the computed value of that expression. op represents floating-point operation in 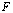 .
.2.4. Matrix Norms
2.4.1. The Singular Value Decomposition (SVD)[3, 15]
- Definition 2.4.1 The compact singular value decomposition or SVD of an
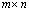 matrix
matrix 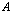 of a rank
of a rank 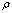 is the decomposition:
is the decomposition: 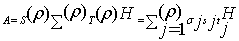 where
where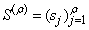 and
and 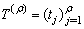 are unitary matrices, that is,
are unitary matrices, that is, 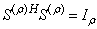 ,
,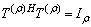 ,
,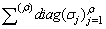 is a diagonal matrix,
is a diagonal matrix, 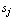 and
and 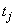 are m- and n-dimensional vectors, respectively, and
are m- and n-dimensional vectors, respectively, and 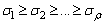 > 0.
> 0. 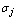 or
or 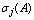 for
for 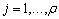 is the
is the 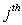 largest singular value of the matrix
largest singular value of the matrix 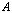 .Definition 2.4.2 The condition number,
.Definition 2.4.2 The condition number, 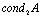 of a matrix
of a matrix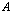 of a rank
of a rank 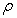 is
is 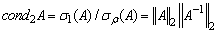 . A matrix is said to be ill conditioned if its condition number is large, that is if
. A matrix is said to be ill conditioned if its condition number is large, that is if 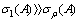 , and is called well conditioned otherwise.Definition 2.4.3[6] The matrix 2-norm
, and is called well conditioned otherwise.Definition 2.4.3[6] The matrix 2-norm 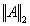 =
= 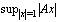 =
= 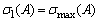 , is also called the spectral norm.
, is also called the spectral norm. 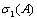 denotes the largest singular value of the matrix
denotes the largest singular value of the matrix 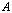 .Remark 2.4.1 The matrix 2-norm satisfies the relation1.
.Remark 2.4.1 The matrix 2-norm satisfies the relation1. 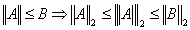 where
where 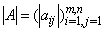 ,
, 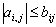 for
for 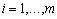 and
and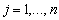 .2.
.2. 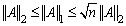 .Lemma 2.3 For a vector norm
.Lemma 2.3 For a vector norm 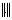 , suppose that
, suppose that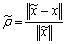 < 1 . Then
< 1 . Then 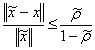 .
.2.5. Numerical Nullity
- Definition 2.5.1 The nullity of
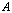 ,
, 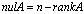 , is the smallest integer
, is the smallest integer 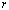 for which a rank
for which a rank 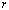 APC
APC 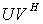 can define a nonsingular A-modification
can define a nonsingular A-modification 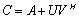 . The nullity of
. The nullity of 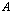 , which is defined as the dimension of the null space can also be defined as the large integer r for which we have
, which is defined as the dimension of the null space can also be defined as the large integer r for which we have 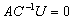 or
or 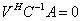 , provided
, provided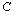 is a nonsingular matrix. In this case,
is a nonsingular matrix. In this case, 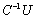 and
and 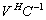 are the right and left null matrix bases for the matrix A.Definition 2.5.2 The numerical nullity of
are the right and left null matrix bases for the matrix A.Definition 2.5.2 The numerical nullity of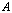 is the number of its small singular values.
is the number of its small singular values.2.6. Convergence
- There is a natural way to extend the notion of limit from
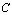 to
to 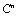 .Definition 2.6.1 Let
.Definition 2.6.1 Let 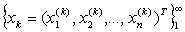 be a sequence of vectors in
be a sequence of vectors in 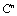 and let
and let 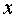
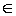
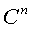 . The sequence
. The sequence 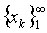 converges componentwise to
converges componentwise to 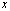 and we write
and we write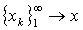 if
if 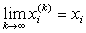 for
for 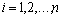 .Here is another way to define convergence in
.Here is another way to define convergence in 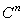 .Definition 2.6.2 Let
.Definition 2.6.2 Let 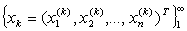 be a sequence of vectors in
be a sequence of vectors in 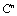 and let
and let 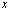
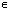
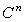 . The sequence
. The sequence 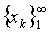 converges normwise to
converges normwise to 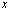 , that is
, that is if and only if
if and only if 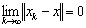 There is no compelling reason to expect the two notions of convergence to be equivalent. In fact for infinite dimensional vector space, they are not.Theorem 2.4[6] Let
There is no compelling reason to expect the two notions of convergence to be equivalent. In fact for infinite dimensional vector space, they are not.Theorem 2.4[6] Let 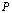
 and suppose that
and suppose that 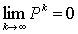 .Then
.Then 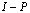 is nonsingular and
is nonsingular and 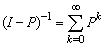 (this sum is called Neumann sum). A sufficient condition for
(this sum is called Neumann sum). A sufficient condition for 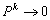 is that
is that 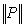 < 1 in some consistent norm, in which case
< 1 in some consistent norm, in which case 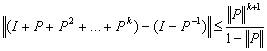 .Corollary 2.5 If
.Corollary 2.5 If 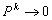 , then
, then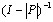 is nonnegative and
is nonnegative and 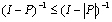 .Theorem 2.6[6] Let
.Theorem 2.6[6] Let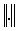 be a matrix norm on
be a matrix norm on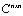 consistent with a vector norm (also denoted
consistent with a vector norm (also denoted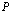
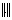 ) and let a matrix
) and let a matrix 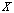
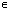
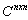 . Let
. Let 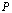 be a square matrix such that
be a square matrix such that 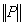 < 1. Then(i) the matrix
< 1. Then(i) the matrix 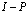 is nonsingular,(ii)
is nonsingular,(ii) 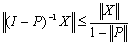 , and(iii)
, and(iii) 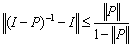 .The following corollary extends Theorem 2.6.Corollary 2.7[6] If
.The following corollary extends Theorem 2.6.Corollary 2.7[6] If 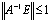 , then
, then 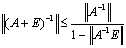 .Moreover,
.Moreover, 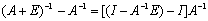 ,so that
,so that 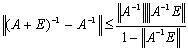 .The corollary remains valid if all occurrences of
.The corollary remains valid if all occurrences of 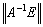 are replaced by
are replaced by 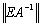 .Theorem 2.8 [8, 17] Let
.Theorem 2.8 [8, 17] Let 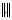 denote a matrix norm and a consistent vector norm. If the matrix
denote a matrix norm and a consistent vector norm. If the matrix 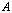 is nonsingular and
is nonsingular and 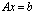 and (i)
and (i) 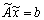 , where
, where 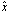 is an approximated value of x, then(ii)
is an approximated value of x, then(ii) 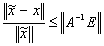 .In addition if
.In addition if 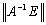 < 1, then
< 1, then 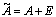 is nonsingular and(iii)
is nonsingular and(iii) 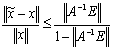 .
.3. The Additive Preconditioning Method, the Schur Aggregation and the Extended Iterative Refinement or Improvement Algorithm
3.1. The Additive Preconditioning Method
- Definition 3.1.1 For a pair of matrices
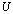 of size
of size 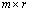 and
and 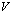 of size
of size 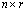 , both having full rank r > 0, the matrix
, both having full rank r > 0, the matrix 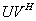 of rank r is an additive preprocessor (APP) of rank r for any
of rank r is an additive preprocessor (APP) of rank r for any 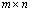 matrix
matrix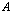 . The matrix
. The matrix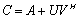 is the A-modification. The matrices
is the A-modification. The matrices 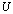 and
and 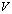 are the generators of the APP, and the transition
are the generators of the APP, and the transition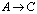 is an A-preprocessing of rank r for the matrix
is an A-preprocessing of rank r for the matrix 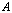 . An APP
. An APP 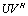 for a matrix A is an additive preconditioning (APC) and an A-preprocessing is an A-preconditioning if
for a matrix A is an additive preconditioning (APC) and an A-preprocessing is an A-preconditioning if 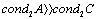 . An APP is an additive compressor (AC) and an A-preprocessing is an A-complementation if the matrix A is rank deficient, whereas the A-modification C has full rank. An APP
. An APP is an additive compressor (AC) and an A-preprocessing is an A-complementation if the matrix A is rank deficient, whereas the A-modification C has full rank. An APP 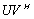 is unitary if the matrices
is unitary if the matrices 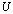 and
and 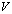 are unitary.Remark 3.1.1 Suppose
are unitary.Remark 3.1.1 Suppose 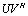 has rank r. Then[3, 18], we expect
has rank r. Then[3, 18], we expect 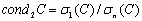 to be to the order of
to be to the order of 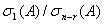 , therefore small if the additive preconditioner
, therefore small if the additive preconditioner 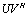 isi) randomii) well conditioned, andiii) properly scaled, that is
isi) randomii) well conditioned, andiii) properly scaled, that is 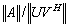 is not large and not small.Additive preconditioning consists in adding a matrix
is not large and not small.Additive preconditioning consists in adding a matrix 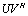 of a small rank to the input matrix
of a small rank to the input matrix 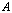 , to decrease its condition number. The A-modification is supposed to generate a well conditioned matrix
, to decrease its condition number. The A-modification is supposed to generate a well conditioned matrix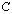 . In practice, to compute the A-modification
. In practice, to compute the A-modification 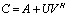 error-free, we fill the generators
error-free, we fill the generators 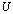 and
and 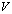 with short binary numbers.
with short binary numbers.3.2. The Schur Aggregation
- The aggregation method consists of transforming an original linear system
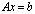 into linear systems of smaller sizes with well conditioned coefficients matrices
into linear systems of smaller sizes with well conditioned coefficients matrices 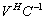 ,
, 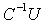 , and
, and 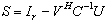 . The aggregation method is a well known technique[3, 14, 15, 18], but aggregation used here both decreases the size of the input matrix and improves its conditioning. One may remark that aggregation can be applied recursively until no ill conditioned matrix appears in the computation.Definition 3.2.1 The Schur aggregation is the process of reducing the linear system
. The aggregation method is a well known technique[3, 14, 15, 18], but aggregation used here both decreases the size of the input matrix and improves its conditioning. One may remark that aggregation can be applied recursively until no ill conditioned matrix appears in the computation.Definition 3.2.1 The Schur aggregation is the process of reducing the linear system 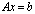 by using the SMW (Sherman-Morrison-Woodbury) formula
by using the SMW (Sherman-Morrison-Woodbury) formula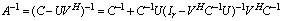 . The matrix
. The matrix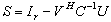 , which is the Schur complement (Gauss transform) of the block
, which is the Schur complement (Gauss transform) of the block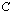 in the block matrix
in the block matrix 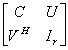 , is called the Schur aggregate. The A-modification
, is called the Schur aggregate. The A-modification 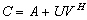 and the Schur aggregate
and the Schur aggregate 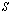 are well conditioned, therefore the numerical problems in the inversion of the matrix A are confined to the computation of the Schur aggregate
are well conditioned, therefore the numerical problems in the inversion of the matrix A are confined to the computation of the Schur aggregate 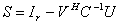 .
.3.3. The Iterative Refinement or Improvement Algorithm
- Let
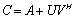 . Then, we apply the Sherman-Morrison -Woodbury (SMW) formula to the original linear system
. Then, we apply the Sherman-Morrison -Woodbury (SMW) formula to the original linear system 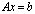 and transform it into better conditioned linear systems of small sizes, with well conditioned matrices
and transform it into better conditioned linear systems of small sizes, with well conditioned matrices 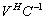 ,
,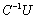 and
and 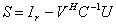 . We solve the original linear system
. We solve the original linear system 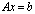 by post-multiplying
by post-multiplying 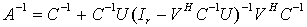 by the vector b. We consider the case where the matrices C and S are well conditioned, whereas the matrices
by the vector b. We consider the case where the matrices C and S are well conditioned, whereas the matrices 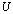 and
and 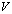 have small rank r, so that we can solve the above linear systems with the matrices
have small rank r, so that we can solve the above linear systems with the matrices 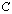 and
and 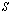 faster and more accurately than the system with the matrix
faster and more accurately than the system with the matrix 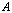 . In this case the original conditioning problems for a linear system
. In this case the original conditioning problems for a linear system 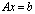 are restricted to the computation of the Schur aggregate
are restricted to the computation of the Schur aggregate 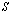 .To compute the Schur aggregate
.To compute the Schur aggregate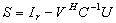 with precision, we begin with computing
with precision, we begin with computing 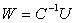 using the iterative refinement or improvement algorithm. We prove that we can get very close to the solution W of the linear system
using the iterative refinement or improvement algorithm. We prove that we can get very close to the solution W of the linear system 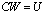 . We closely approximate it by working with numbers rounded to the IEEE standard double precision and using error-free summation. All norms used in this section are the 2-norm. The iterative refinement or improvement algorithm is a technique for improving the computed approximate solution
. We closely approximate it by working with numbers rounded to the IEEE standard double precision and using error-free summation. All norms used in this section are the 2-norm. The iterative refinement or improvement algorithm is a technique for improving the computed approximate solution 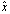 of a linear system
of a linear system 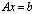 . Iterative refinement or improvement for the Gaussian Elimination (GE) was used in the 1940s on desk calculators, but the first thorough analysis of the method was given by Wilkinson in 1963. The process consists of three steps ([6],[7],[15]).Algorithm 2. Basic iterative refinement or improvement algorithmInput: An
. Iterative refinement or improvement for the Gaussian Elimination (GE) was used in the 1940s on desk calculators, but the first thorough analysis of the method was given by Wilkinson in 1963. The process consists of three steps ([6],[7],[15]).Algorithm 2. Basic iterative refinement or improvement algorithmInput: An 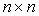 matrix
matrix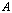 , a computed solution
, a computed solution 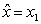 to
to 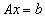 and a vector b.Output: A solution vector
and a vector b.Output: A solution vector 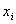 approximating
approximating 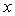 in
in 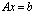 and an error bound
and an error bound 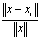 .Initialize:
.Initialize: 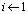 Computations: 1) Compute the residual
Computations: 1) Compute the residual 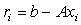 in double precision (
in double precision (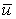 ) 2) Solve
) 2) Solve 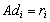 in single precision (u) using the GEPP 3) Update
in single precision (u) using the GEPP 3) Update 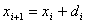 in double precision (
in double precision (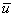 )
)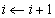 Repeat stages 1-3 until
Repeat stages 1-3 until 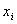 is accurate enough.Output
is accurate enough.Output 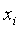 and an error bound.The iterative refinement or improvement algorithm can be rewritten as follows[6].
and an error bound.The iterative refinement or improvement algorithm can be rewritten as follows[6]. 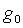 is the error in the computation of
is the error in the computation of 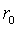 ,
, 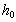 is the error in the computation of
is the error in the computation of 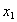 and
and 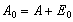 , where
, where 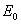 is the perturbation to the matrix A.
is the perturbation to the matrix A. 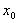 is a computed solution of the linear system
is a computed solution of the linear system 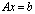 .1)
.1) 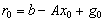 2)
2) 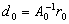 3)
3) 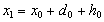 Repeat stages 1-3.The algorithm yields a sequence of approximate solutions
Repeat stages 1-3.The algorithm yields a sequence of approximate solutions 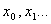 which converges to
which converges to 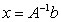 .We use the extension of Wilkinson’s iterative refinement or improvement to compute the matrix
.We use the extension of Wilkinson’s iterative refinement or improvement to compute the matrix 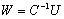 with extended precision. In its classical form, above the algorithm is applied to a single system
with extended precision. In its classical form, above the algorithm is applied to a single system 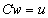 , where
, where 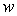 and
and 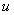 are
are 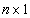 vectors. We applied it to the matrix equation
vectors. We applied it to the matrix equation 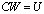 , where the solution we are seeking is the matrix . In its classical version, also the refinement stops when the matrix
, where the solution we are seeking is the matrix . In its classical version, also the refinement stops when the matrix 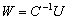 is computed with at most double precision. In order to achieve the high precision in computing W, we apply a variant of the extended iterative refinement or improvement where the residuals dynamically decrease, which is a must for us. We represent the output value as the sum of matrices with fixed-precision numbers.
is computed with at most double precision. In order to achieve the high precision in computing W, we apply a variant of the extended iterative refinement or improvement where the residuals dynamically decrease, which is a must for us. We represent the output value as the sum of matrices with fixed-precision numbers.3.4. The Extended Iterative Refinement or Improvement
- Suppose
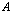 is an ill conditioned non-singular
is an ill conditioned non-singular 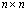 matrix with
matrix with 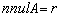 where
where 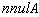 is the numerical nullity of the matrix
is the numerical nullity of the matrix 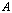 ,
, 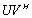 is a random, well conditioned and properly scaled APC of rank r < n, and the well conditioned A-modification
is a random, well conditioned and properly scaled APC of rank r < n, and the well conditioned A-modification 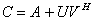 . We use the matrices
. We use the matrices 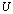 and
and 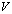 whose entries can be rounded to a fixed (small) number of bits to control or avoid rounding errors in computing the matrix
whose entries can be rounded to a fixed (small) number of bits to control or avoid rounding errors in computing the matrix 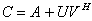 .Surely, small norm perturbations of the generators
.Surely, small norm perturbations of the generators 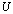 and
and 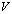 , caused by truncation of their entrees, keep the matrix C well conditioned. We rewrite the iterative refinement or improvement algorithm to solve the linear system
, caused by truncation of their entrees, keep the matrix C well conditioned. We rewrite the iterative refinement or improvement algorithm to solve the linear system 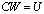 with
with 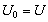 and
and 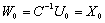 as follows.Algorithm 3.
as follows.Algorithm 3.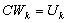 | (0.1) |
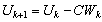 | (0.2) |
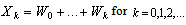 | (0.3) |
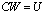 is computed by means of Gaussian Elimination with Partial Pivoting (hereafter GEPP), which is a backward stable process. It is corrupted by rounding errors of the computation of
is computed by means of Gaussian Elimination with Partial Pivoting (hereafter GEPP), which is a backward stable process. It is corrupted by rounding errors of the computation of 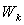 in (0.1), so that the computed matrix
in (0.1), so that the computed matrix 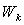 (computed in single precision arithmetic u) turns into
(computed in single precision arithmetic u) turns into 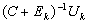 .
. 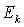 is the perturbation to the matrix C. We can also say equivalently that there exists an error matrix
is the perturbation to the matrix C. We can also say equivalently that there exists an error matrix 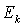 such that
such that 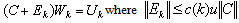 | (0.4) |
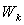 is an exact solution for the approximated problem.
is an exact solution for the approximated problem. 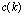 is a constant function of order
is a constant function of order 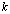 . Another source of error is the computation in (0.2) which, done using double precision arithmetic
. Another source of error is the computation in (0.2) which, done using double precision arithmetic 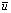 , turns numerically into
, turns numerically into 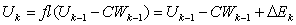 | (0.5) |
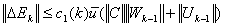 | (0.6) |
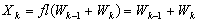 | (0.7) |
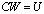 , derived from the ill conditioned linear system
, derived from the ill conditioned linear system 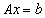 , by applying the following extended iterative refinement or improvement algorithm.
, by applying the following extended iterative refinement or improvement algorithm. 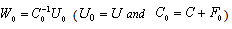
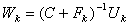 | (0.8) |
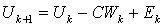 | (0.9) |
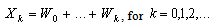 Let
Let 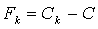 .Theorem 3.1[1]
.Theorem 3.1[1]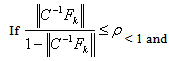 | (0.10) |
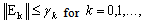 | (0.11) |
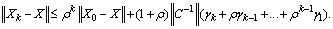 In other words,
In other words, 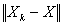 is bounded by
is bounded by 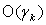 for a certain integer k. Proposition 3.2 Let
for a certain integer k. Proposition 3.2 Let 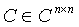 be nonsingular and let consider the linear system
be nonsingular and let consider the linear system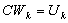 . If
. If 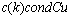 <ρ < 1, then the matrix
<ρ < 1, then the matrix 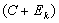 is nonsingular and
is nonsingular and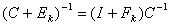 where
where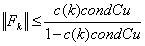 | (0.12) |
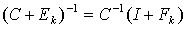 .
.4. Forward Error Analysis
- Our forward error analysis of the extended iterative refinement or improvement algorithm results with the following proposition.Proposition 4.1 (Forward error bound) Let
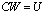 be a linear system derived from an ill conditioned linear system
be a linear system derived from an ill conditioned linear system 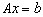 where
where 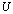 is
is 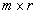 ,
,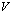 is
is 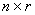 both with full rank r> 0, and
both with full rank r> 0, and 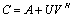 is a well conditioned A-modification. If
is a well conditioned A-modification. If 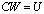 is solved using the extended iterative refinement or improvement algorithm, Algorithm (4.) then for sufficiently large
is solved using the extended iterative refinement or improvement algorithm, Algorithm (4.) then for sufficiently large 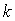 the forward error
the forward error 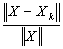 is bounded by
is bounded by 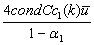 . That is
. That is 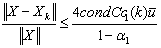 where
where 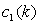 and
and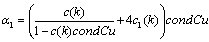 are constant functions of order k. Furthermore we have
are constant functions of order k. Furthermore we have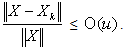 The forward error is bounded by a constant in the order of u which is an important result.Proof: We obtain from equation (0.4),
The forward error is bounded by a constant in the order of u which is an important result.Proof: We obtain from equation (0.4),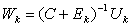 . Since
. Since 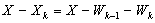 , we get
, we get 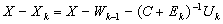 by using (0.4).
by using (0.4). 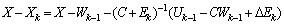 by using (0.5),
by using (0.5),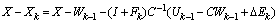 by using (0.12) in Proposition (3.2),
by using (0.12) in Proposition (3.2),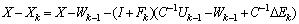 ,
,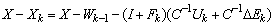 by using (0.2). We have,
by using (0.2). We have, 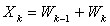 ,
,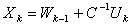 ,
,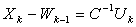 , so that
, so that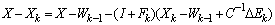 ,
,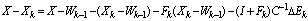 Consequently
Consequently 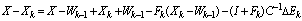
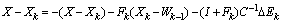 , so
, so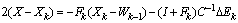 .Without loss of generality we can assume that
.Without loss of generality we can assume that 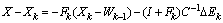 .Recall that
.Recall that 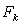 < 1, and take the norm on both sides, to get
< 1, and take the norm on both sides, to get 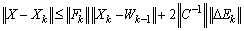 .Recalling (0.6) and (0.7), we deduce that
.Recalling (0.6) and (0.7), we deduce that 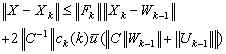 We recall the following inequalities (0.12),
We recall the following inequalities (0.12), 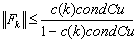 < 1. From (0.7)
< 1. From (0.7) 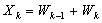 , Therefore
, Therefore 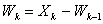 ,
, 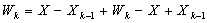
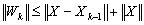 . So
. So 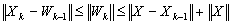 .We recall (0.6)
.We recall (0.6) 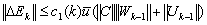 . We also have
. We also have 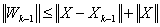
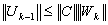
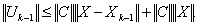
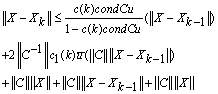
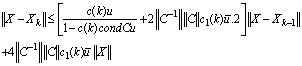
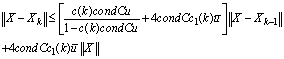
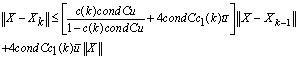
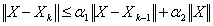 where
where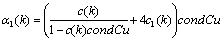 and
and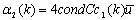 .
. 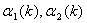 and
and 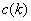 are constant functions of order
are constant functions of order 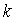 .
.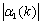 < 1 and
< 1 and 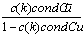 < 1 since C is well conditioned, we deduce that
< 1 since C is well conditioned, we deduce that 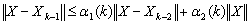 . Therefore,
. Therefore, 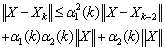 .We also recall that
.We also recall that 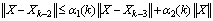 ,so that
,so that 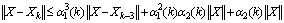 and
and 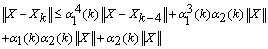 …
…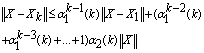
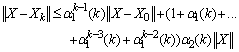
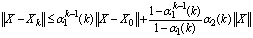 . Therefore,
. Therefore, 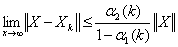
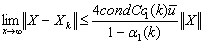
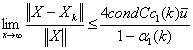 .Therefore for sufficiently largek, we have
.Therefore for sufficiently largek, we have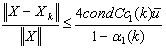 . Moreover,
. Moreover,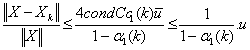 . So,
. So, 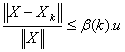 where
where 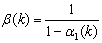 and
and 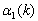 are constant functions of order
are constant functions of order 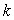 . Therefore,
. Therefore, 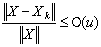 .
.5. Conclusions
- We use the concepts of additive preconditioning and Schur aggregation along with the extended iterative refinement or improvement algorithm to reduce the computation of
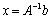 to the computation of the Schur aggregate
to the computation of the Schur aggregate 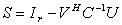 . We solve the linear system
. We solve the linear system 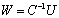 with high precision using the extended iterative refinement or improvement algorithm. We proved in our forward error analysis that the forward error
with high precision using the extended iterative refinement or improvement algorithm. We proved in our forward error analysis that the forward error 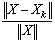 is bounded by
is bounded by 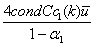 . The forward error can further be bounded by
. The forward error can further be bounded by 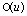 , a constant of order u. These results are in line with Higham’s results ([6], page 234, Theorem 11.1) and constitute another way to prove the convergence of the extended iterative refinement or improvement to a more accurate solution
, a constant of order u. These results are in line with Higham’s results ([6], page 234, Theorem 11.1) and constitute another way to prove the convergence of the extended iterative refinement or improvement to a more accurate solution 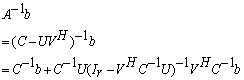 .
.ACKNOWLEDGEMENTS
- The author would like to thank Professor Victor Pan, Distinguished professor of The City University of New York for his support and advice. The author would also like to thank his wife Lisa C. Serme for her support.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML